Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet ECRICOME Maths ECS 2017
Revenir à tous les corrigés des annales maths Ecricome
Exercice 1 : Inégalités de Taylor-Lagrange
1/ a/ Par limite du cours, ![]() . Par composition avec la limite
. Par composition avec la limite ![]() , on a
, on a ![]() .
.
![]()
1/ b/ ![]() est dérivable sur
est dérivable sur ![]() et pour
et pour ![]() ,
, ![]() .
. ![]() ssi
ssi ![]() ssi
ssi ![]() . On a le tableau de variations suivant :
. On a le tableau de variations suivant :
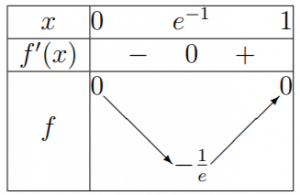
![]() est dérivable sur
est dérivable sur ![]() et pour
et pour ![]() ,
, ![]() .
. ![]() est du signe de
est du signe de ![]() . On a le tableau de variations suivant :
. On a le tableau de variations suivant :
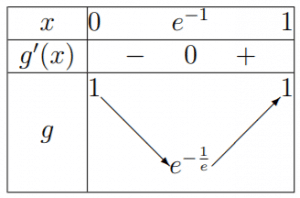
1/ c/ ![]() est continue sur
est continue sur ![]() et admet une limite finie en 0 ;
et admet une limite finie en 0 ; ![]() est donc prolongeable par continuité en 0.
est donc prolongeable par continuité en 0.
![Rendered by QuickLaTeX.com \[\boxed{\text{L'int\'egrale $\int\limits_0^1g(t)\,\mathrm{d}t$ converge.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6b43b027c7367bf892e8bc227bb4ef9c_l3.png)
2/ a/ Soit ![]() . La fonction
. La fonction ![]() est continue sur
est continue sur ![]() et admet une limite finie en 0 (valant 0 si
et admet une limite finie en 0 (valant 0 si ![]() et 1 si
et 1 si ![]() ). La fonction
). La fonction ![]() est donc prolongeable par continuité en 0. L’intégrale
est donc prolongeable par continuité en 0. L’intégrale ![]() converge.
converge.
![]()
2/ b/ Par l’étude de fonction de la question 1.b., on a ![]() pour tout
pour tout ![]() . Pour tout
. Pour tout ![]() , on a donc :
, on a donc :
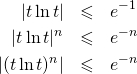
La fonction ![]() est continue sur
est continue sur ![]() et admet une limite finie en 0, donc l’intégrale
et admet une limite finie en 0, donc l’intégrale ![]() converge.
converge.
Par « croissance de l’intégrale », on a : ![]() , soit
, soit ![]() .
.
Par l’inégalité triangulaire :
![Rendered by QuickLaTeX.com \[|u_n|\leqslant \frac 1{n!}\int\limits_0^1|(t\ln t)^n|\,\mathrm{d}t\leqslant \frac{e^{-n}}{n!}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b8ab90ac656ee3d413470845bafc0a50_l3.png)
![]() et
et ![]() . Sans forme indéterminée,
. Sans forme indéterminée, ![]() .
.
Par le théorème d’encadrement,
![]()
2/ c/ ![]() et
et ![]() . Pour calculer cette intégrale, effectuons une intégration par parties, en revenant bien aux intégrales partielles. Soit
. Pour calculer cette intégrale, effectuons une intégration par parties, en revenant bien aux intégrales partielles. Soit ![]() . Les fonctions
. Les fonctions ![]() et
et ![]() suivantes sont de classe
suivantes sont de classe ![]() sur
sur ![]() :
:
![]()
![]() et
et ![]() . On a :
. On a :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int\limits_A^0t\ln t\,\mathrm{d}t&=&\left[\frac {t^2}2\ln t\right]_A^1-\int\limits_A^1\frac t2\,\mathrm{d}t\\&=&-\frac 12A^2\ln A-\left[\frac{t^2}4\right]_A^1\\&=&-\frac 14+\frac{A^2}{4}-\frac{A^2\ln A}2\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cc1bb5685e1cabbb2d438c2cad3a0d6c_l3.png)
Par limite usuelle, ![]() . En faisant tendre
. En faisant tendre ![]() vers 0, nous obtenons
vers 0, nous obtenons
![]()
2/ d/ Soit ![]() . On effectue une intégration par parties avec les fonctions de classe
. On effectue une intégration par parties avec les fonctions de classe ![]() sur
sur ![]() :
:
![]()
![]() et
et ![]() .
.
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int\limits_A^1t^n (\ln t)^n\,\mathrm{d}t&$ $=&\left[\frac{t^{n+1}}{n+1}(\ln t)^n\right]_A^1-\int\limits_A^1\frac{nt^{n+1}(\ln t)^{n-1}}{(n+1)t}\,\mathrm{d}t\\&$ $=&-\frac {A^{n+1}(\ln A)^n}{n+1}-\frac n{n+1}\int\limits_A^1t^n(\ln t)^{n-1}\,\mathrm{d}t$\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-51ef793be10c0e65ad3619d7b9aec1ad_l3.png)
Par limite usuelle (ou croissance comparée) ![]() . En faisant tendre
. En faisant tendre ![]() vers 0, nous obtenons :
vers 0, nous obtenons :
![Rendered by QuickLaTeX.com \[n!u_n=-\frac n{n+1}\int\limits_0^1t^n (\ln t)^{n-1}\,\mathrm{d}t\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8ecb6334107055abd8669dcfcd9823e8_l3.png)
Nous réitérons, comme indiqué, l’intégration par parties sur le segment ![]() , avec les fonctions de classe
, avec les fonctions de classe ![]() sur
sur ![]() :
:
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int\limits_A^1t^n (\ln t)^{n-1}\,\mathrm{d}t&=&\left[\frac{t^{n+1}}{n+1}(\ln t)^{n-1}\right]_A^1-\int\limits_A^1\frac{(n-1)t^{n+1}(\ln t)^{n-2}}{(n+1)t}\,\mathrm{d}t\\&=&-\frac {A^{n+1}(\ln A)^{n-1}}{n+1}-\frac {n(n-1)}{n+1}\int\limits_A^1t^n(\ln t)^{n-2}\,\mathrm{d}t\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c9dda3e6c60927fd811d5d829570e63f_l3.png)
Par limite usuelle (ou croissance comparée) ![]() , et en faisant tendre
, et en faisant tendre ![]() vers 0, nous obtenons :
vers 0, nous obtenons :
![Rendered by QuickLaTeX.com \[n!u_n=\frac {n(n-1)}{(n+1)^2}\int\limits_0^1t^n (\ln t)^{n-2}\,\mathrm{d}t\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b175204ec9862f79370b65fe0ab5f7d4_l3.png)
En continuant ce procédé, nous avons pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[n!u_n=(-1)^{k}\frac{n(n-1)\dots (n-k+1)}{(n+1)^k}\int\limits_0^1t^n (\ln t)^{n-k}\,\mathrm{d}t\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e348b05fd041b09d590d4540de00e28d_l3.png)
En particulier, ![]() .
.
![Rendered by QuickLaTeX.com \[\boxed{\text{$\forall n\in\mathbb{N}$, $u_n=\frac{(-1)^n}{(n+1)^{n+1}}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-90060266ea4304b6e9e9fb85322888a9_l3.png)
2/ e/ Pour ![]() ,
, ![]() .
.
La série de Riemann ![]() converge. On a
converge. On a ![]() .
.
Par le théorème de comparaison des séries à termes positifs, la série ![]() converge. Par propriété relative à la convergence absolue,
converge. Par propriété relative à la convergence absolue,
![]()
2/ f/ Avec calcul vectoriel :
function S = somme(n)
k = 0:n
u = (-1).^k ./(k+1).^(k+1)
S = sum(u)
endfunction
Par une boucle for :
function S = sommebis(n)
S = 0
for k = 0:n
S = S + (-1)^k/(k+1)^(k+1)
end
endfunction
3/ a/ Soit ![]() . Considérons
. Considérons ![]()
et ![]() . La fonction
. La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() , et pour tout
, et pour tout ![]() ,
, ![]() . Par l’inégalité de Taylor-Lagrange à l’ordre
. Par l’inégalité de Taylor-Lagrange à l’ordre ![]() , pour tout
, pour tout ![]() , on a :
, on a :
![Rendered by QuickLaTeX.com \[\left|f(x)-\sum\limits_{k=0}^n\frac{f^{(k)}(0)}{k!}(x-0)^k\right|\leqslant \frac{|x-0|^{n+1}}{(n+1)!}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a53924c24d30859d68c25578775abd18_l3.png)
Pour tout entier naturel ![]() ,
, ![]() .
.
Pour ![]() , on a
, on a ![]() , puis
, puis ![]() et donc :
et donc :
![Rendered by QuickLaTeX.com \[\forall x\in I,\quad \left|e^x-\sum\limits_{k=0}^n \frac{x^k}{k!}\right|\leqslant \frac{1}{e^{n+1}(n+1)!}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-bc4c8167d8618a311e050f8251314fe2_l3.png)
3/ b/ Soit ![]() . Par l’étude de la question 1.b.,
. Par l’étude de la question 1.b., ![]() . On peut appliquer le résultat de la question précédente :
. On peut appliquer le résultat de la question précédente :
![Rendered by QuickLaTeX.com \[\left|e^{x\ln x}-\sum\limits_{k=0}^n \frac{(x\ln x)^k}{k!}\right|\leqslant \frac{1}{e^{n+1}(n+1)!}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a0c915a8a661334bceec77922fb8ee1f_l3.png)
Les fonctions ![]() et
et ![]() sont continues sur
sont continues sur ![]() et l’intégrale
et l’intégrale ![]() est convergente. Par le théorème de comparaison pour des intégrales de fonctions continues positives, l’intégrale
est convergente. Par le théorème de comparaison pour des intégrales de fonctions continues positives, l’intégrale ![]() converge.
converge.
Par « croissance de l’intégrale » :
![Rendered by QuickLaTeX.com \[\int\limits_0^1\left|e^{x\ln x}-\sum\limits_{k=0}^n \frac{(x\ln x)^k}{k!}\right|\,\mathrm{d}x\leqslant \int\limits_0^1\frac{1}{e^{n+1}(n+1)!}\,\mathrm{d}x \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-08ce8b8750900c110c1a83d851dca209_l3.png)
soit
![Rendered by QuickLaTeX.com \[\int\limits_0^1\left|e^{x\ln x}-\sum\limits_{k=0}^n \frac{(x\ln x)^k}{k!}\right|\,\mathrm{d}x\leqslant\frac{1}{e^{n+1}(n+1)!} \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d5fe3e901a36c146369c16eaac1b229f_l3.png)
Par ailleurs, par linéarité pour des intégrales convergentes, ![]() .\\
.\\
On termine par l’inégalité triangulaire :
![Rendered by QuickLaTeX.com \[\left|I-S_n\right|\leqslant \int\limits_0^1\left|e^{x\ln x}-\sum\limits_{k=0}^n \frac{(x\ln x)^k}{k!}\right|\,\mathrm{d}x\leqslant\frac{1}{e^{n+1}(n+1)!}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-bb1901dd7be4268b24d8abae0430105c_l3.png)
3/ c/ Sans forme indéterminée, ![]() . Le théorème d’encadrement appliqué à l’encadrement de la question précédente donne :
. Le théorème d’encadrement appliqué à l’encadrement de la question précédente donne : ![]() .
.
Ainsi ![]() . Le changement d’indice
. Le changement d’indice ![]() donne :
donne :
![Rendered by QuickLaTeX.com \[I=-\sum\limits_{n=1}^{+\infty}\frac{(-1)^n}{n^n}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8797f76a3cf843d61921ae040bcad58d_l3.png)
3/ d/
function I = estimation(eps)
n = 0
while 1/ (exp(n+1)*factorial(n+1)) >= eps
n = n+1
end
I = somme(n)
endfunction
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Matrice Symétrique
1/ a/ ![]() est une matrice symétrique réelle donc
est une matrice symétrique réelle donc ![]() est diagonalisable et il existe une matrice orthogonale
est diagonalisable et il existe une matrice orthogonale ![]() et une matrice diagonale
et une matrice diagonale ![]() telles que
telles que ![]() .
.
1/ b/ On a, en notant ![]() les colonnes de
les colonnes de ![]() :
:

![]()
Comme ![]() , on a
, on a ![]() et
et
![]()
Par le théorème du rang, ![]() .
.
![]()
1/ c/ Deux matrices semblables ont même trace, donc ![]() .
.
Par la question précédente, il existe un réel ![]() tel que
tel que 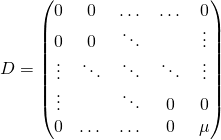 . On a
. On a ![]() . Finalement,
. Finalement, ![]() et
et
![Rendered by QuickLaTeX.com \[D=\begin{pmatrix}0&0&\dots &\dots &0\\0&0&\ddots&&\vdots\\\vdots & \ddots &\ddots&\ddots &\vdots\\\vdots & &\ddots &0&0\\0&\dots & \dots &0&n\end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b0ce407a577285dd5b6445054ae6221a_l3.png)
2/ a/ Développons le carré :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left( \sum\limits_{i=1}^n x_i\right)^2&=&\left( \sum\limits_{i=1}^n x_i\right)\left( \sum\limits_{j=1}^n x_j\right)=\sum\limits_{(i,j)\in[\![1,n]\!]^2}x_ix_j\\&=&\sum\limits_{(i,j)\in[\![1,n]\!]^2, \; i<j}x_ix_j+\sum\limits_{i=1}^n x_i^2+\sum\limits_{(i,j)\in[\![1,n]\!]^2, \; j<i}x_ix_j\\&&\text{on change d'indice dans la derni\`ere somme : $i'=j$ et $j'=i$}\\&=&\sum\limits_{(i,j)\in[\![1,n]\!]^2, \; i<j}x_ix_j+\sum\limits_{i=1}^n x_i^2+\sum\limits_{(i,j)\in[\![1,n]\!]^2, \; i'<j'}x_{j'}x_{i'}\\&=&\sum\limits_{(i,j)\in[\![1,n]\!]^2, \; i<j}x_ix_j+\sum\limits_{i=1}^n x_i^2+\sum\limits_{(i,j)\in[\![1,n]\!]^2, \; i'<j'}x_{i'}x_{j'}\\&=&2\sum\limits_{(i,j)\in[\![1,n]\!]^2, \; i<j}x_ix_j+\sum\limits_{i=1}^n x_i^2\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-54be2d70f99011099f9725b0db4ddf84_l3.png)
On a bien
![Rendered by QuickLaTeX.com \[f(x_1,x_2,\dots, x_n)=\frac 12\left[\left( \sum\limits_{i=1}^n x_i\right)^2-\sum\limits_{i=1}^n x_i^2\right]\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a7c8b5120a43b2c0e3a9f1eb21c1e99a_l3.png)
2/ b/ La matrice 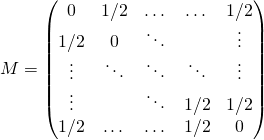 est une matrice (symétrique) telle que
est une matrice (symétrique) telle que ![]() pour tout
pour tout ![]() .
.
2/ c/ On a ![]() .
.
2/ d/ On a ![]() .
.
![Rendered by QuickLaTeX.com \[M=P\Delta { }^tP\text{ avec }\Delta = \begin{pmatrix}-1/2&0&\dots &\dots &0\\0&-1/2&\ddots&&\vdots\\\vdots & \ddots &\ddots&\ddots &\vdots\\\vdots & &\ddots &-1/2&0\\0&\dots & \dots &0&(n-1)/2\end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-96114fcd01f441566b251cd45602704e_l3.png)
En tant que fonction polynomiale de
L’ensemble
Par le théorème des bornes atteintes,
2/ e/ Soit ![]() .
.
Posons ![]() . Par b. et d., nous avons
. Par b. et d., nous avons ![]() . Par calcul matriciel,
. Par calcul matriciel,
![]()
Par ailleurs, ![]() car
car ![]() . Donc
. Donc ![]() , puis :
, puis :
![]()
Nous avons ![]() , soit
, soit ![]() . On en déduit l’encadrement de
. On en déduit l’encadrement de ![]() :
:
![]()
Ceci ne nous fournit qu’un minorant et un majorant de ![]() sur
sur ![]() .
.
Soit ![]() un vecteur propre de norme 1 associé à la valeur propre
un vecteur propre de norme 1 associé à la valeur propre ![]() de
de ![]() . Nous avons
. Nous avons ![]() .
.
![]()
Soit ![]() un vecteur propre de norme 1 associé à la valeur propre
un vecteur propre de norme 1 associé à la valeur propre ![]() de
de ![]() . Nous avons de même
. Nous avons de même ![]() .
.
![]()
3/ a/ ![]() est une matrice symétrique réelle : elle est diagonalisable et il existe
est une matrice symétrique réelle : elle est diagonalisable et il existe ![]() matrice réelle d’ordre
matrice réelle d’ordre ![]() orthogonale et
orthogonale et ![]() matrice diagonale d’ordre
matrice diagonale d’ordre ![]() telles que
telles que ![]() .
.
Comme ![]() a toutes ses valeurs propres positives, les coefficients diagonaux de
a toutes ses valeurs propres positives, les coefficients diagonaux de ![]() sont positifs, et chacun est le carré d’une racine carrée. Il existe
sont positifs, et chacun est le carré d’une racine carrée. Il existe ![]() réels tels que :
réels tels que :
![Rendered by QuickLaTeX.com \[A=P\begin{pmatrix}r_1^2&0&\dots &\dots &0\\0&r_2^2&\ddots&&\vdots\\\vdots & \ddots &\ddots&\ddots &\vdots\\\vdots & &\ddots &0&0\\0&\dots & \dots &0&r_n^2\end{pmatrix}{ }^tP\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3dd213df04a822f11acbed0c79b57474_l3.png)
Posons 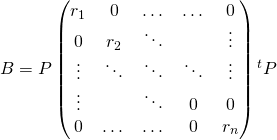 .
.
Nous avons :

car ![]() .
.
![]()
3/ b/ Remarquons qu’avec le choix de la matrice ![]() précédemment effectué,
précédemment effectué, ![]() est symétrique. En effet, en notant
est symétrique. En effet, en notant  , on a
, on a ![]() .
.
Les valeurs propres de ![]() sont non nulles donc
sont non nulles donc ![]() est bijectif. De même, les valeurs propres de
est bijectif. De même, les valeurs propres de ![]() sont les
sont les ![]() , donc
, donc ![]() est inversible et
est inversible et ![]() est bijectif.
est bijectif.
La matrice de ![]() relativement à une base orthonormée est symétrique, donc
relativement à une base orthonormée est symétrique, donc ![]() est un endomorphisme symétrique. Pour les mêmes raisons, les endomorphismes
est un endomorphisme symétrique. Pour les mêmes raisons, les endomorphismes ![]() ,
, ![]() ,
, ![]() sont des endomorphismes symétriques.
sont des endomorphismes symétriques.
Pour ![]() et
et ![]() vecteurs de
vecteurs de ![]() , on a :
, on a :
![]()
Par l’inégalité de Cauchy-Schwarz, on a alors ![]() . Enfin,
. Enfin,
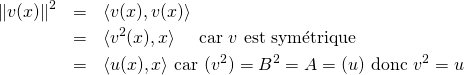
et

![]()
3/ c/ Soit ![]() un vecteur non nul de
un vecteur non nul de ![]() . Posons
. Posons ![]() . Comme
. Comme ![]() est injectif (0 n’est pas valeur propre de
est injectif (0 n’est pas valeur propre de ![]() ), son noyau est réduit à
), son noyau est réduit à ![]() , et comme
, et comme ![]() , on a
, on a ![]() . On a :
. On a :
![]()
Il y a égalité dans l’inégalité trouvée plus haut.
Soit ![]() un vecteur de
un vecteur de ![]() de norme 1. On a par la question précédente (on prend
de norme 1. On a par la question précédente (on prend ![]() ):
):
![]()
Soit ![]() une valeur propre de
une valeur propre de ![]() , et
, et ![]() un vecteur propre de
un vecteur propre de ![]() de norme 1 associé à cette valeur propre (un tel vecteur existe, car si
de norme 1 associé à cette valeur propre (un tel vecteur existe, car si ![]() est un vecteur propre,
est un vecteur propre, ![]() est encore vecteur propre et il est normé).
est encore vecteur propre et il est normé).
On a ![]() donc
donc ![]() . Ainsi :
. Ainsi :
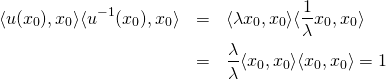
En conclusion, pour tout vecteur ![]() de
de ![]() de norme 1, on a :
de norme 1, on a :
![]()
et le minimum de l’ensemble ![]() est
est ![]() .
.
4/ a/ On a ![]() donc
donc ![]() est inversible. De plus,
est inversible. De plus,
![]()
4/ b/ ![]() est valeur propre de
est valeur propre de ![]() ssi
ssi ![]() est non inversible ssi
est non inversible ssi ![]() ssi
ssi ![]() .
.
![Rendered by QuickLaTeX.com \[Sp(A)=\left\{\frac{3-\sqrt 5}2,\frac{3+\sqrt 5}2\right\}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-73e6b7a620bd337402da4cf2efd0dbad_l3.png)
Comme ![]() , on a
, on a ![]() .
.
![]()
4/ c/ Faisons le lien avec la question 3. La matrice ![]() est symétrique réelle à valeurs propres strictement positives. Soit
est symétrique réelle à valeurs propres strictement positives. Soit ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() .
.
On a ![]() et
et ![]() ,
,
ce qui fait que ![]() .
.
Quant à la contrainte ![]() , elle équivaut à
, elle équivaut à ![]() , ou encore
, ou encore ![]() .
.
Le résultat de la question 3.c. nous donne que la valeur du minimum de ![]() sous la contrainte
sous la contrainte ![]() est 1.
est 1.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Problème : Densité de probabilité
Partie A :
1/ ![]()
![]() est continue sur
est continue sur ![]() et
et ![]() .
.
En réalité, comme ![]() ,
, ![]() est continue sur
est continue sur ![]() , mais cela ne nous sert pas ici.
, mais cela ne nous sert pas ici.
![]()
![]() est positive sur
est positive sur ![]() .
.
![]() Soit
Soit ![]() .
.
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int\limits_0^Ag_a(x)\,\mathrm{d}x&=&\left[-e^{-x^2/(2a^2)}\right]_0^A=1--e^{-A^2/(2a^2)}\\\lim\limits_{A\to +\infty}\int\limits_0^Ag_a(x)\,\mathrm{d}x&=&1\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-29e93c9fd1f779c29000ae37944e932f_l3.png)
donc l’intégrale ![]() converge et vaut 1.
converge et vaut 1.
Comme ![]() est nulle sur
est nulle sur ![]() , l’intégrale
, l’intégrale ![]() converge et vaut 0.
converge et vaut 0.
L’intégrale ![]() converge et vaut 1.
converge et vaut 1.
Par ces trois points,
![]()
2/ a/ Une densité de ![]() est :
est :
![]()
On a ![]() et
et ![]() .
.
![]()
2/ b/ Puisque ![]() admet un moment d’ordre 2, l’intégrale définissant
admet un moment d’ordre 2, l’intégrale définissant ![]() converge absolument et on a :
converge absolument et on a :
![Rendered by QuickLaTeX.com \[\int\limits_{-\infty}^{+\infty}\frac{x^2}{\sqrt {2\pi a^2}}e^{-x^2/(2a^2)}\,\mathrm{d}x=a^2\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a4350b76fd6d2bc1dc99207053806d22_l3.png)
L’intégrande est pair ; par parité :
![Rendered by QuickLaTeX.com \[2\int\limits_{0}^{+\infty}\frac{x^2}{\sqrt {2\pi a^2}}e^{-x^2/(2a^2)}\,\mathrm{d}x=a^2\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e637f9c1253a56d438249ca2a56eee9a_l3.png)
donc l’intégrale ![]() converge (absolument) et vaut
converge (absolument) et vaut ![]() soit
soit ![]() .
.
Comme ![]() est nulle sur
est nulle sur ![]() , on a la convergence absolue de l’intégrale
, on a la convergence absolue de l’intégrale ![]() et sa valeur.
et sa valeur.
![Rendered by QuickLaTeX.com \[\boxed{\text{$Z_a$ admet une esp\'erance, et cette esp\'erance vaut $a\sqrt{\frac{\pi }{2}}$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b62e9f3bbdcfd406d830be02001446ab_l3.png)
2/ c/ ![]() admet un moment d’ordre 2 ssi l’intégrale
admet un moment d’ordre 2 ssi l’intégrale ![]() converge absolument ssi l’intégrale
converge absolument ssi l’intégrale ![]() converge.
converge.
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() , strictement croissante sur
, strictement croissante sur ![]() , bijective de
, bijective de ![]() dans
dans ![]() . Le changement de variables
. Le changement de variables ![]() est permis dans cette intégrale impropre
est permis dans cette intégrale impropre ![]() ; les intégrales avant et après changement de variables sont de même nature, et égales en cas de convergence. L’intégrale après changement de variable est
; les intégrales avant et après changement de variables sont de même nature, et égales en cas de convergence. L’intégrale après changement de variable est ![]() , convergente.
, convergente.
Donc ![]() admet un moment d’ordre 2, donc une variance, et
admet un moment d’ordre 2, donc une variance, et ![]() .
.
![]()
![Rendered by QuickLaTeX.com \[\boxed{\text{$Z_a$ admet une variance, valant $\frac{(4-\pi)a^2}{2}$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9886ec774f34929bb6dd204db26a34dd_l3.png)
Partie B :
1/
function X = tirage(n)
urnes = zeros(1,n)
X = 1
choix = floor(rand()*n) + 1
disp(choix)
while max(urnes)<2
urnes(choix) = urnes(choix) + 1
choix = floor(rand()*n) + 1
disp(choix)
X = sum(urnes)
//si on préfère X = X+1, prendre l’initialisation X = 0 au lieu de X=1
end
endfunction
2/ Ici ![]() . On ne dispose que d’une urne. Elle contient deux boules pour la première fois au deuxième tirage.
. On ne dispose que d’une urne. Elle contient deux boules pour la première fois au deuxième tirage. ![]() est la variable aléatoire certaine égale à 2. Son espérance est 2 et sa variance est 0.
est la variable aléatoire certaine égale à 2. Son espérance est 2 et sa variance est 0.
3/ Ici ![]() . On dispose de deux urnes. Notons
. On dispose de deux urnes. Notons ![]() la variable aléatoire égale au numéro de l’urne choisie au
la variable aléatoire égale au numéro de l’urne choisie au ![]() -ième placement de boule.
-ième placement de boule.
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}{[X_2=2]}&=&\left([N_1=1]\cap [N_2=1]\right)\cup \left( [N_1=2]\cap [N_2=2]\right)\\P(X_2=2)&=&P(N_1=1)P(N_2=1)+P(N_1=2)P(N_2=2)=\frac 12\times \frac 12+\frac 12\times \frac 12=\frac 12\\{[X_2=3]}&=&\left([N_1=1]\cap [N_2=2]\right)\cup \left( [N_1=2]\cap [N_2=1]\right)\\P(X_2=2)&=&P(N_1=1)P(N_2=2)+P(N_1=2)P(N_2=1)=\frac 12\times \frac 12+\frac 12\times \frac 12=\frac 12\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-559d0282e7017ce9933e0d7f810f7264_l3.png)
La variable aléatoire ![]() est à valeurs dans
est à valeurs dans ![]() et prend la valeur 1 avec probabilité 1/2 ; elle suit la loi de Bernoulli de paramètre 1/2.
et prend la valeur 1 avec probabilité 1/2 ; elle suit la loi de Bernoulli de paramètre 1/2.
![]()
Par linéarité de l’espérance, ![]() ; par propriété
; par propriété ![]() , on a
, on a ![]() .
.
![]()
4/ a/ Au plus rapide, on peut choisir deux fois de suite la même urne, et ![]() prend la valeur 2. Au plus long, on peut choisir chacune des urnes une seule fois (cela prend
prend la valeur 2. Au plus long, on peut choisir chacune des urnes une seule fois (cela prend ![]() tirages) et le tirage suivant aboutit à une urne contenant 2 boules pour la première fois ;
tirages) et le tirage suivant aboutit à une urne contenant 2 boules pour la première fois ; ![]() prend la valeur
prend la valeur ![]() . Les situations intermédiaires sont possibles (pour
. Les situations intermédiaires sont possibles (pour ![]() , on choisit pendant
, on choisit pendant ![]() placements des urnes différentes, et le tirage
placements des urnes différentes, et le tirage ![]() , on prend une urne déjà utilisée).
, on prend une urne déjà utilisée).
![]()
4/ b/ Pour ![]() , on a :
, on a :
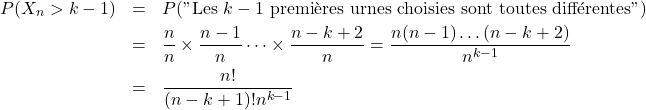
Cette relation est en réalité valable aussi pour ![]() puisque
puisque ![]() .
.
On a ![]() et l’union est constituée d’événements disjoints.
et l’union est constituée d’événements disjoints.
Donc ![]() .
.
Pour ![]() ,
,
![Rendered by QuickLaTeX.com \begin{eqnarray*}P(X_n=k)&=&\frac{n!}{(n-k+1)!n^{k-1}}-\frac{n!}{(n-k)!n^{k}}\\&=&\frac{n!}{(n-k+1)!n^{k}}\left[n-(n-k+1)\right]=\frac{n!(k-1)}{(n-k+1)!n^{k}}\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7c7eab507ba01c6d8c4eddb9bff26e5c_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\text{Pour $k\in [\![2,n+1]\!]$, \quad $P(X_n=k)=\frac{n!(k-1)}{(n-k+1)!n^{k}}$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cccc2f292ca54076dfb8dadd82d8cc4f_l3.png)
4/ c/ Pour ![]() ,
, ![]() prend un nombre fini de valeurs, et admet donc une espérance.
prend un nombre fini de valeurs, et admet donc une espérance.
![]()
4/ d/ function E = esperance(n)
facto = prod([1:n])
fac = facto
somme = 0
puissance = n
for k = 2:(n+1)
puissance = puissance *n
fac = fac/(n-k+2)
somme = somme + k*(k-1)/(puissance * fac)
end
E = facto * somme
endfunction
Partie C :
1/ La fonction ![]() est concave sur
est concave sur ![]() , donc sa courbe représentative est en-dessous de ses tangentes, et en particulier de sa tangente en 0, d’équation
, donc sa courbe représentative est en-dessous de ses tangentes, et en particulier de sa tangente en 0, d’équation ![]() .
.
![]()
Introduisons ![]() .
. ![]() est dérivable sur
est dérivable sur ![]() et pour
et pour ![]() réel de cet intervalle,
réel de cet intervalle, ![]() .
.![]() est donc croissante sur
est donc croissante sur ![]() . Comme
. Comme ![]() , on a
, on a ![]() pour
pour ![]() .
.
![]()
2/ Soient ![]() et
et ![]() tels que
tels que ![]() . Pour tout
. Pour tout ![]() , on a
, on a ![]() . Par la question précédente :
. Par la question précédente :
![]()
On somme ces inégalités pour ![]() allant de 0 à
allant de 0 à ![]() :
:
![Rendered by QuickLaTeX.com \[\sum\limits_{k=0}^m\left(-\frac kn-\frac {k^2}{n^2}\right)\leqslant \sum\limits_{k=0}^m\ln (1-\frac kn)\leqslant \sum\limits_{k=0}^m-\frac kn\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-52d3e94878f05b634dfa4bd180b97d86_l3.png)
Par linéarité de la somme :
![Rendered by QuickLaTeX.com \[-\frac 1n\sum\limits_{k=0}^mk-\frac {1}{n^2}\sum\limits_{k=0}^mk^2\leqslant \sum\limits_{k=0}^m\ln (1-\frac kn)\leqslant -\frac 1n\sum\limits_{k=0}^mk\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0591de79552ee35e7267069bd30f8cb0_l3.png)
Par les formules de sommation : ![]() et
et ![]() , on obtient le résultat demandé :
, on obtient le résultat demandé :
![]()
3/ Pour ![]() ,
, ![]() et
et ![]() n’est pas une valeur de
n’est pas une valeur de ![]() . Ainsi
. Ainsi ![]() .
.
![]()
4/ a/ ![]() est dans cette question strictement positif.
est dans cette question strictement positif.![]() . Par composition avec la limite
. Par composition avec la limite ![]() , on a :
, on a :
![]()
On a l’encadrement :
![]()
puis
![]()
Comme ![]() , on applique le théorème d’encadrement, et on obtient :
, on applique le théorème d’encadrement, et on obtient : ![]() .
.
![]()
4/ b/ Comme ![]() , il existe un rang à partir duquel
, il existe un rang à partir duquel ![]() .
.
Comme ![]() et
et ![]() , il existe un rang à partir duquel
, il existe un rang à partir duquel ![]() .
.
Par ces deux informations,
![]()
4/ c/ Soit ![]() et
et ![]() .
.
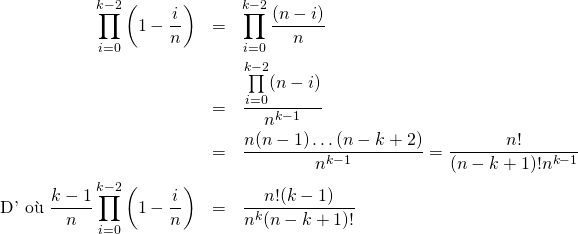
Par la question B.4.b., on a bien ![]() .
.
4/ d/ Par propriété de l’exponentielle :
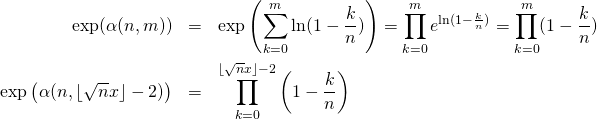
Pour ![]() ,
, ![]() est un entier compris entre 2 et
est un entier compris entre 2 et ![]() , donc compris entre 2 et
, donc compris entre 2 et ![]() ; c’est une valeur de
; c’est une valeur de ![]() , et la formule de la question c. s’applique.
, et la formule de la question c. s’applique.
![]()
4/ e/ On rappelle que ![]() est un réel strictement positif fixé. Dans les négligeabilités et équivalences ci-dessous,
est un réel strictement positif fixé. Dans les négligeabilités et équivalences ci-dessous, ![]() tend vers
tend vers ![]() .
.
Par 4.a., ![]() . On a
. On a ![]() ou encore
ou encore ![]() .
.
Donc ![]() , et
, et ![]() .
.
![]()
De même, ![]() , et par produit d’équivalents,
, et par produit d’équivalents, ![]() , et cette quantité est de limite
, et cette quantité est de limite ![]() .
.
Toujours par produit d’équivalents,
![]()
et cette quantité est de limite nulle.
Relisons l’encadrement de la question 2. appliqué au cas de ![]() . Les calculs précédents nous assurent que les deux membres encadrants tendent vers
. Les calculs précédents nous assurent que les deux membres encadrants tendent vers ![]() quand
quand ![]() tend vers
tend vers ![]() . Par le théorème d’encadrement,
. Par le théorème d’encadrement, ![]() . Par composition avec exp, continue en
. Par composition avec exp, continue en ![]() , on a :
, on a :
![]()
Par produit d’équivalents, ![]() .
.
![Rendered by QuickLaTeX.com \[\boxed{\text{Pour $x>0$, $\lim\limits_{n\to +\infty}\sqrt nP(X_n=\lfloor \sqrt nx\rfloor)=x\exp(-\frac{x^2}2)$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-142f3dc307c2dec2d366e6e37d0112eb_l3.png)
On s’aperçoit que
![]()
Partie D
1/ a/ Soit ![]() et
et ![]() .
.
![]()
![Rendered by QuickLaTeX.com \[\boxed{\text{Pour $k\in\mathbb{Z}$ et $n\in \mathbb{N}^*$, l'ensemble des r\'eels $x$ tels que $\lfloor \sqrt nx\rfloor =k$ est $[\frac k{\sqrt n},\frac{k+1}{\sqrt n}[$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f120a35068c9e599662815ccceef0d3a_l3.png)
1/ b/ ![]() .
.![]() ssi
ssi ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
À l’aide des intervalles trouvés en question précédente :
![Rendered by QuickLaTeX.com \[f_n(x)=\begin{cases}0&\text{ si }x<\frac 2{\sqrt n}\\\sqrt n P(X_n=2)&\text{ si }\frac 2{\sqrt n}\leqslant x<\frac{3}{\sqrt n}\\\sqrt n P(X_n=3)&\text{ si }\frac 3{\sqrt n}\leqslant x<\frac{4}{\sqrt n}\\\vdots &\\\sqrt n P(X_n=n+1)&\text{ si }\frac {n+1}{\sqrt n}\leqslant x<\frac{n+2}{\sqrt n}\\0&\text{ si }x\geqslant \frac{n+2}{\sqrt n}\end{cases}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-dd7519ef3439dbdd0f3df9d6e48f6aa1_l3.png)
où chacune des probabilités peut être exprimée à l’aide de la question 4.b. de la partie B (mais ce n’est pas nécessaire).![]() est donc une fonction positive sur
est donc une fonction positive sur ![]() , et continue sur
, et continue sur ![]() privé d’un nombre fini de points.
privé d’un nombre fini de points.
L’intégrale de ![]() sur
sur ![]() converge (c’est l’intégrale d’une fonction continue par morceaux sur le segment
converge (c’est l’intégrale d’une fonction continue par morceaux sur le segment ![]() ,
, ![]() étant nulle hors de ce segment) et on a :
étant nulle hors de ce segment) et on a :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int\limits_{-\infty}^{+\infty}f_n(t)\,\mathrm{d}t&=&0+\int\limits_{2/\sqrt n}^{3/\sqrt n}\sqrt nP(X_n=2)\,\mathrm{d}t+\int\limits_{3/\sqrt n}^{4/\sqrt n}\sqrt nP(X_n=3)\,\mathrm{d}t+\dots \\&& +\int\limits_{(n+1)/\sqrt n}^{(n+2)/\sqrt n}\sqrt nP(X_n=n+1)\,\mathrm{d}t+0\\&=&P(X_n=2)+P(X_n=3)+\dots + P(X_n=n+1)=1\text{ car }X_n(\Omega)=[\![2,n+1]\!]\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-401da3a15d6356500b8975dd4240dc83_l3.png)
![]()
2/ a/ Soit ![]() et
et ![]() .
.![]() Premier cas :
Premier cas : ![]() .
.
L’entier ![]() est strictement inférieur à l’entier
est strictement inférieur à l’entier ![]() . On a donc
. On a donc ![]() . Ainsi
. Ainsi ![]() puis
puis ![]() .
. ![]()
![]() Deuxième cas :
Deuxième cas : ![]() .
.
L’entier ![]() est strictement supérieur à l’entier
est strictement supérieur à l’entier ![]() donc
donc ![]() . On a donc
. On a donc ![]() puis
puis ![]() .
.![]()
![]() Troisième cas :
Troisième cas : ![]() .
.
On a : ![]() donc
donc ![]() , et
, et ![]() .
.
![Rendered by QuickLaTeX.com \[\boxed{\text{$P(U\leqslant \sqrt nx-k)=\begin{cases}0&\text{ si }k>\lfloor \sqrt nx\rfloor\\\sqrt nx-\lfloor \sqrt nx\rfloor&\text{ si }k=\lfloor \sqrt nx\rfloor\\1&\text{ si }k<\lfloor \sqrt nx\rfloor\end{cases}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8e130a70228f3fdf1db4bbb0e0ed48d6_l3.png)
2/ b/ Soit ![]() réel. Appliquons la formule des probabilités totales avec le système complet d’événements
réel. Appliquons la formule des probabilités totales avec le système complet d’événements ![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}P(Y_n\leqslant x)&=&\sum\limits_{k=2}^{n+1}P([X_n=k]\cap [Y_n\leqslant x])\\&=&\sum\limits_{k=2}^{n+1}P\left([X_n=k]\cap \left[\frac{k+U}{\sqrt n}\leqslant x\right]\right)\\&=&\sum\limits_{k=2}^{n+1}P([X_n=k]\cap [U\leqslant \sqrt nx-k])\quad \text{ et par ind\'ependance de $X_n$ et $U$ :}\\&=&\sum\limits_{k=2}^{n+1}P(X_n=k)P(U\leqslant \sqrt nx-k)\\&&\text{(on utilise la question pr\'ec\'edente) :}\\&=&\sum\limits_{k\in [\![2,n+1]\!],\; k<\sqrt nx}P(X_n=k)P(U\leqslant \sqrt nx-k)+P(X_n=\lfloor \sqrt nx\rfloor)(\sqrt nx-\lfloor \sqrt nx\rfloor)+0\\&=&P(X_n<\sqrt nx)+P(X_n=\lfloor \sqrt nx\rfloor)(\sqrt nx-\lfloor \sqrt nx\rfloor)\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7604baab6c3931ef3448c264b6706db8_l3.png)
(cette relation est valable même si ![]() ; auquel cas la deuxième probabilité est nulle).
; auquel cas la deuxième probabilité est nulle).
Par ailleurs, exprimons ![]() .
.
Pour ![]() ,
,
![Rendered by QuickLaTeX.com \[\int\limits_{-\infty}^xf_n(t)\,\mathrm{d}t=0=0+0=P(X_n<\sqrt nx)+P(X_n=\lfloor \sqrt nx\rfloor)(\sqrt nx-\lfloor \sqrt nx\rfloor)=P(Y_n\leqslant x)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e97a023bb5a33d07f13d8c0a88143787_l3.png)
Et pour ![]() , par l’expression de
, par l’expression de ![]() présentée en question 1.b. et par la relation de Chasles :
présentée en question 1.b. et par la relation de Chasles :
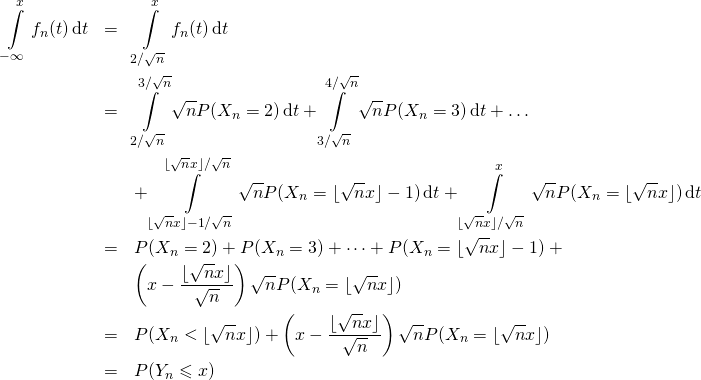
![Rendered by QuickLaTeX.com \[\boxed{\text{Pour tout r\'eel $x$, $P(Y_n\leqslant x)=\int\limits_{-\infty}^xf_n(t)\,\mathrm{d}t$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-adf08b75d4e2db9b733a15849d77f940_l3.png)
2/ c/ Par 1.b., ![]() est une densité de probabilité, et on peut considérer
est une densité de probabilité, et on peut considérer ![]() une variable aléatoire de densité
une variable aléatoire de densité ![]() .
.
Par la question précédente, ![]() et
et ![]() ont même fonction de répartition, et par conséquent même loi.
ont même fonction de répartition, et par conséquent même loi.![]() est donc une variable aléatoire à densité, de densité
est donc une variable aléatoire à densité, de densité ![]() .
.
Par la partie C., pour tout réel ![]() ,
, ![]() .
.
La variable aléatoire ![]() est une variable aléatoire à densité, de densité
est une variable aléatoire à densité, de densité ![]() .
.
Par le résultat admis en début de partie D., la suite de variables aléatoires ![]() converge en loi vers
converge en loi vers ![]() .
.
![]()
3/ a/ Soit ![]() une suite de variables aléatoires convergeant en loi vers une variable aléatoire
une suite de variables aléatoires convergeant en loi vers une variable aléatoire ![]() , et
, et ![]() une suite de variables aléatoires convergeant en probabilité vers une variable aléatoire constante égale à
une suite de variables aléatoires convergeant en probabilité vers une variable aléatoire constante égale à ![]() .
.
Alors la suite de variables aléatoires ![]() converge en loi vers la variable aléatoire
converge en loi vers la variable aléatoire ![]() , et la suite de variables aléatoires
, et la suite de variables aléatoires ![]() converge en loi vers la variable aléatoire
converge en loi vers la variable aléatoire ![]() .
.
3/ b/ ![]() . On vient de voir que
. On vient de voir que ![]() convergeait en loi vers
convergeait en loi vers ![]() . Montrons que
. Montrons que ![]() converge en probabilité vers 0. Soit
converge en probabilité vers 0. Soit ![]() .
.
![]()
et cette probabilité est nulle lorsque
Il existe un rang à partir duquel
La suite
Par le théorème de Slutsky,
![Rendered by QuickLaTeX.com \[\boxed{\text{la suite $\left(\frac{X_n}{\sqrt n}\right)$ converge en loi vers $Y=Z_1$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5c7d2db41c49975235f2fb4e0ef31243_l3.png)

