Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EM Lyon Maths ECS 2016 (ECG approfondies)
Revenir à tous les corrigés des annales maths BCE
Problème 1.
Partie I : Un exemple
1/ 
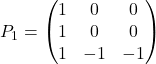 et
et  .
.
2/ a/ ![]() ,
, ![]() ,
, ![]() et
et ![]() .
.
b/ Comme les matrices ![]() et
et ![]() commutent, la formule du binôme donne :
commutent, la formule du binôme donne :
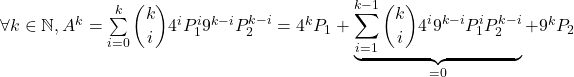
car en raison de 2(a) : ![]() .
.
3/ Avec ![]() ,
, ![]() puisque
puisque ![]() et
et ![]() commutent. Donc
commutent. Donc ![]() .
.
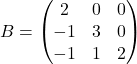 vérifie
vérifie ![]() .
.
4/ Comme ![]() est triangulaire, ses valeurs propres sont ses coefficients diagonaux :
est triangulaire, ses valeurs propres sont ses coefficients diagonaux : ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie II : Étude des puissances de 
5/ Soit ![]() un polynôme quelconque de
un polynôme quelconque de ![]() .
.
![]()
![]()
6/ ![]() puisque les
puisque les ![]() sont les racines de
sont les racines de ![]() .
.
7/ a/ Soit ![]() .
.
Si ![]() ,
, ![]() est une racine de
est une racine de ![]() donc
donc ![]() par définition de
par définition de ![]() .
.
Si ![]() ,
, ![]()
b/ Soit ![]() .
. 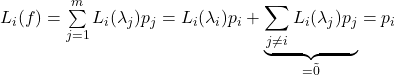 .
.
8/ a/ ![]() .
.
b/ ![]() Soit
Soit ![]() .
. ![]() avec
avec ![]() .
.
Donc ![]() , et ainsi
, et ainsi ![]() .
.
![]() Réciproquement, comme
Réciproquement, comme ![]() , on a
, on a ![]() .
.
Par double inclusion, ![]() .
.
9/ a/ ![]() .
.
b/ Par 6. et 7.b et 9.a : ![]() .
.
Soit ![]() . Alors il existe
. Alors il existe ![]() tel que
tel que ![]() .
.
![]() , donc
, donc ![]() .
.
Ainsi ![]() .
.
10/ Observons que, pour tout ![]() de
de ![]() ,
, ![]() entraîne
entraîne ![]() .
.
Ainsi ![]() , donc
, donc ![]() est une valeur propre de
est une valeur propre de ![]() .
.
Ensuite ![]() , et
, et ![]() .
.
Ainsi, ![]() . Comme par propriété du cours, les sous-espaces propres
. Comme par propriété du cours, les sous-espaces propres ![]() sont en somme directe, ils sont supplémentaires,
sont en somme directe, ils sont supplémentaires, ![]() est diagonalisable et
est diagonalisable et ![]() .
.
Resta à justifier que ![]() .
.
On a par 9(b), ![]() .
.
Par 8(b) et le début de 10, ![]() .
.
Ceci n’est possible que si ![]() (en effet, si pour un seul des
(en effet, si pour un seul des ![]() , on avait
, on avait ![]() , on aurait
, on aurait ![]() … ce qui est impossible !)
… ce qui est impossible !)
Par conséquent, ![]() : les
: les ![]() sont les sous-espaces propres de
sont les sous-espaces propres de ![]() .
.
11/ a/ On peut observer que ![]() et
et ![]() commutent car :
commutent car :

Alors, pour tout ![]() de
de ![]() ,
, ![]() donc
donc ![]() , or les sous-espaces propres sont en somme directe, donc
, or les sous-espaces propres sont en somme directe, donc ![]() , donc
, donc ![]() .
.
b/ Pour tout ![]() de
de ![]() ,
, ![]() .
.
c/ Pour tout ![]() de
de ![]() ,
, ![]() .
.
12/ ![]() Raisonnons par récurrence, l’initialisation est assurée par les hypothèses sur
Raisonnons par récurrence, l’initialisation est assurée par les hypothèses sur ![]() . Voyons l’hérédité.
. Voyons l’hérédité.
Soit ![]() . Supposons
. Supposons ![]() .
.
Alors ![]()
Ceci achève la récurrence et : ![]() .
.
![]() Le même raisonnement qu’en 5. donne cette fois :
Le même raisonnement qu’en 5. donne cette fois :
![]() .
.
Partie III : Intervention d’un produit scalaire
13/ Soit ![]() ,
, ![]() et
et ![]() trois vecteurs de
trois vecteurs de ![]() et
et ![]() un réel.
un réel.
![]()
![]()
![]() est linéaire à gauche.
est linéaire à gauche.
![]() est symétrique par symétrie du produit scalaire
est symétrique par symétrie du produit scalaire ![]() .
.
![]() .
.
Supposons ![]() . Alors
. Alors ![]() , donc
, donc ![]() , donc
, donc ![]() .
.
Or par 8(a), ![]() , donc
, donc ![]() .
.
Ainsi ![]() est une forme bilinéaire symétrique définie positive, c’est-à-dire un produit scalaire sur
est une forme bilinéaire symétrique définie positive, c’est-à-dire un produit scalaire sur ![]() .
.
14/ Soit ![]() et
et ![]() deux vecteurs de
deux vecteurs de ![]() .
.
![]()
![]()
Donc ![]() , ce qui prouve que
, ce qui prouve que ![]() est un endomorphisme symétrique pour le produit scalaire
est un endomorphisme symétrique pour le produit scalaire ![]() .
.
Ceci démontre à nouveau que ![]() est diagonalisable.
est diagonalisable.
15/ On sait déjà, d’après 11(b), que ![]() est un projecteur, sur
est un projecteur, sur ![]() . Il suffit que
. Il suffit que ![]() soit symétrique pour
soit symétrique pour ![]() pour que
pour que ![]() soit le projecteur orthogonal sur
soit le projecteur orthogonal sur ![]() , toujours pour le produit scalaire
, toujours pour le produit scalaire ![]() .
.
Soit ![]() .
.
![]()
![]() est bien symétrique pour
est bien symétrique pour ![]() :
: ![]() est le projecteur orthogonal sur
est le projecteur orthogonal sur ![]() pour le produit scalaire
pour le produit scalaire ![]() .
.
Problème 2 :
Partie I : Étude d’une fonction définie par la somme d’une série
1/ Soit ![]() .
.
![]() , donc le terme général
, donc le terme général ![]() diverge.
diverge.
De même, si ![]() , le terme général
, le terme général ![]() diverge.
diverge.
Puisqu’une condition nécessaire de convergence de la série est la convergence du terme général (vers ![]() ), si
), si ![]() , alors la série
, alors la série ![]() diverge.
diverge.
2/ a/ ![]() car
car ![]() .
.
![]() car
car ![]() .
.
![]() .
.
![]() est croissante,
est croissante, ![]() est décroissante, et leur différence tend vers
est décroissante, et leur différence tend vers ![]() : ces suites sont adjacentes, donc convergent, vers une même limite, notée
: ces suites sont adjacentes, donc convergent, vers une même limite, notée ![]() .
.
b/ Soit ![]() .
.
Comme ![]() ,
, ![]() .
.
Comme ![]() ,
, ![]() .
.
Prenons ![]() . Soit
. Soit ![]() .
.
![]() Si
Si ![]() est pair,
est pair, ![]() s’écrit
s’écrit ![]() avec
avec ![]() donc
donc ![]() .
.
![]() Si
Si ![]() est impair,
est impair, ![]() s’écrit
s’écrit ![]() avec
avec ![]() donc
donc ![]() .
.
Conclusion : ![]() .
.
c/ Ainsi, ![]() converge vers
converge vers ![]() , et comme
, et comme ![]() est la suite des sommes partielles de la série
est la suite des sommes partielles de la série ![]() , cette série converge.
, cette série converge.
d/ Comme ![]() est croissante de limite
est croissante de limite ![]() ,
, ![]() .
.
Comme ![]() est décroissante de limite
est décroissante de limite ![]() ,
,
![]() .
.
e/ Soit ![]() .
.
![]() Si
Si ![]() est pair, écrivons
est pair, écrivons ![]() . Par (d),
. Par (d), ![]() .
.
Donc ![]() , et comme
, et comme ![]() ,
,
![]() .
.
![]() Si
Si ![]() est impair, écrivons
est impair, écrivons ![]() . Par (d),
. Par (d), ![]() .
.
Donc ![]() , et comme
, et comme ![]() ,en passant à la valeur absolue,
,en passant à la valeur absolue, ![]() .
.
Dans tous les cas, ![]() .
.
f/
function s=serie(x,e)
n=1
s=1
while (1/(n+1)\textasciicircum x)>e then
n=n+1
s=s+(-1)\textasciicircum(n+1)/(n\textasciicircum x)
end
endfunction
3/ Notons, pour ![]() ,
, ![]() . Alors
. Alors ![]() est la somme des
est la somme des ![]() pondérés d’un signe « – » lorsque
pondérés d’un signe « – » lorsque ![]() est pair.
est pair.
On peut la calculer en prenant la somme des termes d’indices impairs moins celle des termes d’indices pairs :
![]() .
.
On peut aussi la calculer en sommant tous les ![]() sans distinction de parité et en retranchant deux fois la somme des termes d’indices pairs :
sans distinction de parité et en retranchant deux fois la somme des termes d’indices pairs :
![]()
4/ a/ La seconde relation de 3. donne, avec ![]() ,
,
![]() , puis en décalant l’indice de
, puis en décalant l’indice de ![]() ,
,
![]() .
.
b/ On reconnaît dans cette dernière expression la somme de Riemann d’ordre ![]() de la fonction continue
de la fonction continue ![]() .
.
Par continuité de ![]() , le théorème des sommes de Riemann assure que
, le théorème des sommes de Riemann assure que ![]() converge et que :
converge et que :
![]() .
.
5/ 3. avec ![]() donne
donne ![]() .
.
En passant à la limite lorsque ![]() tend vers
tend vers ![]() ,
,
![]() .
.
Partie II : Étude d’une fonction définie par une intégrale
6/ La fonction intégrée est continue et positive sur ![]() .
.
![]()
![]() , or
, or ![]() , que l’on peut écrire
, que l’on peut écrire ![]() , converge si, et seulement si,
, converge si, et seulement si, ![]() , c’est-à-dire
, c’est-à-dire ![]() . Par équivalence de fonctions positives,
. Par équivalence de fonctions positives, ![]() converge si, et seulement si,
converge si, et seulement si, ![]() .
.
![]()
![]() en
en ![]() .
.
Or, lorsque ![]() ,
, ![]() existe puisque
existe puisque ![]() existe.
existe.
Par équivalence de fonctions positives, si ![]() ,
, ![]() existe.
existe.
![]() Ainsi,
Ainsi, ![]() existe si, et seulement si,
existe si, et seulement si, ![]() .
.
7/ a/ Par somme de termes d’une suite géométrique :
![]()
En multipliant par ![]() :
:
![]() … ce qu’il fallait démontrer !
… ce qu’il fallait démontrer !
b/ Le changement de variable ![]() est admissible puisque de classe C1 et bijectif (strictement croissant car
est admissible puisque de classe C1 et bijectif (strictement croissant car ![]() ). Par ce changement,
). Par ce changement, ![]() devient
devient ![]() . Par linéarité, on reconnaît
. Par linéarité, on reconnaît ![]() , qui existe. Par le théorème de changement de variable,
, qui existe. Par le théorème de changement de variable, ![]() existe et vaut
existe et vaut ![]() .
.
c/ Comme ![]() puisque
puisque ![]() , et
, et ![]() existe, donc par comparaison de fonctions positives,
existe, donc par comparaison de fonctions positives, ![]() existe.
existe.
![]() , donc par croissante de l’intégrale, et par le calcul de 7.(b),
, donc par croissante de l’intégrale, et par le calcul de 7.(b), ![]() .
.
Et comme ![]() puisque
puisque ![]() , on a, par encadrement,
, on a, par encadrement, ![]() .
.
d/ Par les questions précédentes (et par linéarité de l’intégrale),
![]()
![]()
En passant à la limite lorsque ![]() tend vers
tend vers ![]() ,
, ![]() .
.
8/ ![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie III : Étude d’une variable aléatoire
9/  .
.
10/ ![]() est continue et positive sur
est continue et positive sur ![]() .
.
Soit ![]() .
.
![Rendered by QuickLaTeX.com \int_{A} ^{B} f(t)dt f(t)dt=\left[-\dfrac1{1+e^t}\right]_A^B=-\dfrac1{1+e^B}+\dfrac1{1+e^A}\underset{\begin{array}{cc}A\to-\infty\\B\to+\infty\end{array}}{\longrightarrow}1](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-bdbcd8b6308364a2a8602a9013608398_l3.png) .
.
Donc ![]() existe et vaut
existe et vaut ![]() .
.
Ainsi ![]() est une densité d’une variable aléatoire.
est une densité d’une variable aléatoire.
11/ Le calcul précédent avec ![]() et
et ![]() donne :
donne :
![]() .
.
12/ a/ ![]() est continue et positive sur
est continue et positive sur ![]() .
.
![]() et
et ![]() existe (c’est
existe (c’est ![]() ).
).
Par équivalence de fonctions positives, ![]() existe.
existe.
Puisque ![]() est paire,
est paire, ![]() a la même parité que l’entier
a la même parité que l’entier ![]() : paire si
: paire si ![]() est pair et impaire sinon.
est pair et impaire sinon.
Du coup, comme ![]() existe,
existe, ![]() existe.
existe.
Ainsi ![]() admet un moment d’ordre
admet un moment d’ordre ![]() .
.
b/ Comme ![]() est une fonction impaire et intégrable sur
est une fonction impaire et intégrable sur ![]() , son intégrale sur
, son intégrale sur ![]() est nulle.
est nulle.
Autrement dit, ![]() .
.
c/ ![]() par parité.
par parité.
Soit ![]() . Effectuons une intégration par parties avec
. Effectuons une intégration par parties avec ![]() et
et ![]() de classe C1 sur
de classe C1 sur ![]() .
.
![]()
En faisant tendre ![]() vers
vers ![]() ,
, ![]() .
.
Donc ![]() .
.
13/ ![]() par 12.(b).
par 12.(b).
![]() .
.
14/ a/ ![]() Comme pour tout
Comme pour tout ![]()
![]() ,
, ![]() .
.
![]()
Par indépendance des ![]() ,
,
![]() .
.
![]()
![]() et :
et :
![]()
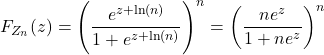
b/ Soit ![]() . Déterminons
. Déterminons ![]() .
.
![]()
Comme ![]() ,
, ![]() .
.
![]() .
.
Donc ![]() .
.
Comme ![]() est une fonction de classe C1 sur
est une fonction de classe C1 sur ![]() , croissante (par composition de deux fonctions décroissantes ou par le signe de sa dérivée – voir l’expression de
, croissante (par composition de deux fonctions décroissantes ou par le signe de sa dérivée – voir l’expression de ![]() ci-après), de limites
ci-après), de limites ![]() en
en ![]() et
et ![]() en
en ![]() ,
, ![]() converge en loi vers une variable aléatoire à densité de fonction de répartition
converge en loi vers une variable aléatoire à densité de fonction de répartition ![]() .
.
Une densité de cette variable est ![]() .
.

