Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EM Lyon Maths ECS 2017 (ECG Approfondies)
Revenir à tous les corrigés des annales maths BCE
Problème I. Matrice, Polynome, Intégrale
Partie I : Étude d’un exemple
1/ La matrice ![]() est triangulaire avec un 0 sur la diagonale donc elle n’est pas inversible. Elle a une colonne nulle et les deux autres ne sont pas proportionnelles donc son rang est 2.
est triangulaire avec un 0 sur la diagonale donc elle n’est pas inversible. Elle a une colonne nulle et les deux autres ne sont pas proportionnelles donc son rang est 2.
2/ La matrice ![]() est triangulaire donc ses valeurs propres sont les coefficients sur sa diagonale donc le spectre de la matrice
est triangulaire donc ses valeurs propres sont les coefficients sur sa diagonale donc le spectre de la matrice ![]() est
est ![]() . Comme elle est dans
. Comme elle est dans ![]() avec 3 valeurs propres, elle est diagonalisable dans
avec 3 valeurs propres, elle est diagonalisable dans ![]() et ses sous-espaces propres sont de dimension 1.
et ses sous-espaces propres sont de dimension 1.
3/ Il est immédiat que 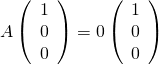 donc
donc ![]() qui est non nul est un vecteur propre de
qui est non nul est un vecteur propre de ![]() associé à 0, il formera la première colonne de
associé à 0, il formera la première colonne de ![]()
Pour trouver un vecteur propre de ![]() associé à 2, on résout
associé à 2, on résout 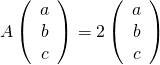 d’inconnues
d’inconnues ![]() dans
dans ![]() On obtient le système
On obtient le système
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l} -b=2a\\2b-4c=2b\\6c=2c\end{array}\right. \Longleftrightarrow \left\{\begin{array}{l} b=-2a\\c=0\end{array}\right.\Longleftrightarrow\left(\begin{array}{ccc} a\\b\\c\end{array}\right)=a\left(\begin{array}{ccc} 1\\-2\\0\end{array}\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-79696c4ade805665446371bdec1711c4_l3.png)
Donc
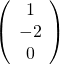 qui est non nul est un vecteur propre de
qui est non nul est un vecteur propre de Pour trouver un vecteur propre de ![]() associé à 6, on résout
associé à 6, on résout 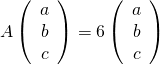 d’inconnues
d’inconnues ![]() dans
dans ![]() On obtient le système :
On obtient le système :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l} -b=6a\\2b-4c=6b\\6c=6c\end{array}\right. \Longleftrightarrow \left\{\begin{array}{l} b=-6a\\c=-b\end{array}\right.\Longleftrightarrow\left(\begin{array}{ccc} a\\b\\c\end{array}\right)=a\left(\begin{array}{ccc} 1\\-6\\6\end{array}\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0a35b4034594d4d1fa3ae0053fe7b3e1_l3.png)
Donc
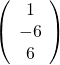 qui est non nul est un vecteur propre de
qui est non nul est un vecteur propre de On pose
![Rendered by QuickLaTeX.com \[\boxed{\text{$P=\left(\begin{array}{ccc} 1&1&1\\0&-2&-6\\0&0&6\end{array}\right)$ et $D=\left(\begin{array}{ccc} 0&0&0\\0&2&0\\0&0&6\end{array}\right)$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a3ff30c4fcb6202b3f9a565dc729a3e7_l3.png)
Le cours de maths assure que ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie II : Étude d’un endomorphisme d’un espace de polynômes
4/ Pour tout polynôme ![]() de
de ![]() donc
donc ![]() est bien un polynôme comme dérivée d’un polynôme. De plus
est bien un polynôme comme dérivée d’un polynôme. De plus ![]() donc
donc ![]() donc
donc ![]() car
car ![]() est de degré 2.
est de degré 2.
Donc ![]() donc
donc ![]()
Montrons que ![]() est linéaire. Soit
est linéaire. Soit ![]() On utilise la linéarité de la dérivation ainsi
On utilise la linéarité de la dérivation ainsi
![]()
![]()
Donc
![]()
5/ On a ![]() Pour
Pour ![]()
![]()
La matrice ![]() de
de ![]() dans la base
dans la base ![]() est donc triangulaire avec des termes diagonaux de la forme
est donc triangulaire avec des termes diagonaux de la forme ![]() où
où ![]() Il y a deux termes non nuls sur chaque colonne sauf sur la première qui est nulle.
Il y a deux termes non nuls sur chaque colonne sauf sur la première qui est nulle.
![Rendered by QuickLaTeX.com \[M=\left(\begin{array}{ccccccc} 0&-1&\hdots&0&\hdots&\hdots&0\\0&2& \hdots &\hdots &\hdots&\hdots &\hdots\\0&\hdots & \ddots &-k^2 &\hdots&\hdots &\hdots\\0&\hdots & 0 &k(k+1) &\hdots&\hdots &\hdots\\0&\hdots & \hdots &0 &\hdots&\hdots &\hdots\\0&\hdots & \hdots & &\hdots&\hdots &0\\ 0&\hdots & \hdots &\hdots &\hdots&n(n-1) &-n^2\\0&\hdots & \hdots &\hdots &\hdots&0 &n(n+1) \end{array}\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f2a308a4bd32efefb5ef4aa00823fc2f_l3.png)
6/ ![]() n’est pas bijectif car son noyau contient 1. On sait que
n’est pas bijectif car son noyau contient 1. On sait que
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\text{$\hbox{Im}(T)=\hbox{Vect}\left(\left(k(k+1)X^k-k^2X^{k-1}\right)_{1\leqslant k\leqslant n}\right).$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5ab6cdcd74cea47bd71b72cf24916c03_l3.png)
Ainsi la famille ![]() engendre
engendre ![]() , elle contient
, elle contient ![]() polynômes non nuls et étagés en degrés donc elle est libre et forme une base de
polynômes non nuls et étagés en degrés donc elle est libre et forme une base de ![]() qui est donc de rang
qui est donc de rang ![]()
Le théorème du rang appliqué à ![]() sur
sur ![]() de dimension finie
de dimension finie ![]() indique alors que
indique alors que ![]() est de dimension 1 donc tout polynôme non nul de
est de dimension 1 donc tout polynôme non nul de ![]() forme une base de
forme une base de ![]() . Or le polynôme
. Or le polynôme ![]() est dans ce noyau donc
est dans ce noyau donc ![]() est une base de
est une base de ![]()
Bilan :
![]()
7/ La matrice ![]() est triangulaire donc son spectre est formé des termes diagonaux c’est-à-dire
est triangulaire donc son spectre est formé des termes diagonaux c’est-à-dire ![]() Comme la fonction
Comme la fonction ![]() est strictement croissante sur
est strictement croissante sur ![]() , elle est injective sur
, elle est injective sur ![]() donc l’ensemble
donc l’ensemble ![]() contient autant de termes que l’ensemble
contient autant de termes que l’ensemble ![]() c’est-à-dire
c’est-à-dire ![]()
Comme ![]() est de dimension
est de dimension ![]() , l’endomorphisme
, l’endomorphisme
![]()
Partie III : Équivalent de  lorsque
lorsque  tend vers
tend vers 
8/ Soit ![]() et
et ![]() .
.
![]()
![]() existe et est à valeur réelle car c’est l’intégrale d’une fonction continue sur un segment.
existe et est à valeur réelle car c’est l’intégrale d’une fonction continue sur un segment.![]() La commutativité du produit dans
La commutativité du produit dans ![]() assure que
assure que ![]()
![]() la linéarité de l’intégration assure que
la linéarité de l’intégration assure que ![]()
![]() On a
On a ![]() car c’est l’intégrale d’une fonction positive avec des bornes dans l’ordre croissant.
car c’est l’intégrale d’une fonction positive avec des bornes dans l’ordre croissant.![]() Si
Si ![]() est le polynôme nul, alors
est le polynôme nul, alors ![]()
Réciproquement si ![]() alors
alors ![]() comme
comme ![]() est une fonction continue, positive et que
est une fonction continue, positive et que ![]() on sait que
on sait que ![]() est nulle sur
est nulle sur ![]() par stricte positivité de l’intégrale.
par stricte positivité de l’intégrale.
Donc ![]() a une infinité de racines donc c’est le polynôme nul, de même pour
a une infinité de racines donc c’est le polynôme nul, de même pour ![]()
Finalement ![]() est une forme bilinéaire symétrique définie positive sur
est une forme bilinéaire symétrique définie positive sur ![]() donc c’est un produit scalaire sur
donc c’est un produit scalaire sur ![]() .
.
9/ Soit ![]()
On fait une intégration par parties avec :
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]()
Les fonctions ![]() sont polynomiales donc
sont polynomiales donc ![]() sur
sur ![]() Ainsi
Ainsi
![]()
10/ Vu les rôles symétriques de ![]() et
et ![]() dans cette dernière expression, il est clair que
dans cette dernière expression, il est clair que ![]() est un endomorphisme symétrique de
est un endomorphisme symétrique de ![]() pour le produit scalaire
pour le produit scalaire ![]()
En effet :
![]()
Donc
![]()
11/ a/ Soit ![]() car
car ![]() est positif sur
est positif sur ![]() ainsi que
ainsi que ![]() , c’est donc l’intégrale d’une fonction positive avec des bornes dans l’ordre croissant.
, c’est donc l’intégrale d’une fonction positive avec des bornes dans l’ordre croissant.
11/ b/ Soit ![]() de
de ![]() . On a
. On a
![]()
Cela équivaut à dire que le polynôme ![]() a une infinité de racines c’est-à-dire qu’il est nul c’est-à-dire que
a une infinité de racines c’est-à-dire qu’il est nul c’est-à-dire que ![]() est le polynôme nul car
est le polynôme nul car ![]() n’est pas le polynôme nul.
n’est pas le polynôme nul.
Finalement :
![]()
Partie IV : Retour sur l’exemple de la partie I
12/ ![]() donc on obtient la matrice
donc on obtient la matrice ![]()
13/ Avec la question 3 de la partie I, on sait que ![]()
![]() est vecteur propre de
est vecteur propre de ![]() associé à 0
associé à 0![]()
![]() est vecteur propre de
est vecteur propre de ![]() associé à 2
associé à 2![]()
![]() est vecteur propre de
est vecteur propre de ![]() associé à 6
associé à 6
Ces vecteurs propres sont deux à deux orthogonaux car ![]() est symétrique pour
est symétrique pour ![]() et car les valeurs propres sont deux à deux distinctes.
et car les valeurs propres sont deux à deux distinctes.
Ils forment une base de ![]() il reste à les normer en les divisant par leurs normes respectives. On montre facilement que, pour tout
il reste à les normer en les divisant par leurs normes respectives. On montre facilement que, pour tout ![]()
![]()
![]() est de norme 1 car
est de norme 1 car ![]()
![]() Par ailleurs :
Par ailleurs :
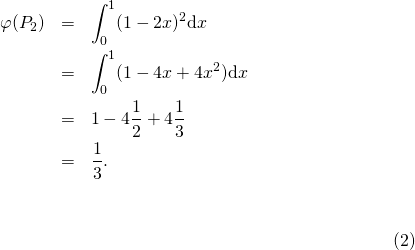
Donc ![]()
Et
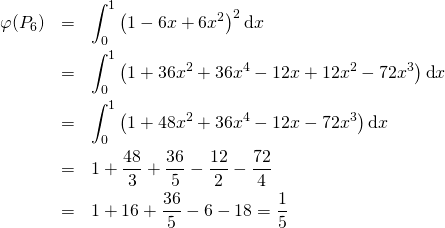
Donc ![]()
Donc on pose
![]()
14/ La matrice de ![]() dans
dans ![]() est
est 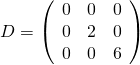 .
.
On pose ![]() tel que
tel que
![Rendered by QuickLaTeX.com \[\hbox{Mat}_{{\cal C}}(V)=\left(\begin{array}{ccc} 0&0&0\\0&\sqrt{2}&0\\0&0&\sqrt{6}\end{array}\right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-fd591c0b35384d6c15011348ef9d753e_l3.png)
ainsi
On utilise le fait que ![]() est une base orthonormale de
est une base orthonormale de ![]() formées de vecteurs propres de
formées de vecteurs propres de ![]() on pose
on pose ![]() et
et ![]() alors
alors
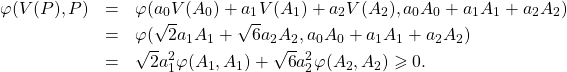
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Problème 2 : Limite d’une intégrale et suites de variables aléatoires
Partie I : Premières propriétés de la fonction 
1/ On pose, pour tout ![]() sur
sur ![]() Comme
Comme ![]() est polynomiale strictement positive sur
est polynomiale strictement positive sur ![]() on peut composer par
on peut composer par ![]() et
et ![]() est
est ![]() (et aussi
(et aussi ![]() ) sur
) sur ![]() On peut multiplier par
On peut multiplier par ![]() et composer par exponentielle, la fonction
et composer par exponentielle, la fonction ![]() est positive et
est positive et ![]() (et aussi
(et aussi ![]() ) sur
) sur ![]()
On a ![]() car
car ![]()
Comme ![]() , on a
, on a ![]() , donc
, donc ![]() converge donc par comparaison
converge donc par comparaison ![]() converge.
converge.
Par continuité sur un segment, ![]() existe donc par somme
existe donc par somme ![]() converge.
converge.
Bilan :
![]()
2/ Soit ![]() on a
on a ![]() , pour tout
, pour tout ![]() donc
donc ![]() On compose par exponentielle qui est croissante sur
On compose par exponentielle qui est croissante sur ![]() ainsi
ainsi ![]() .
.
On intègre de 0 à ![]() avec des bornes dans l’ordre croissant, cela donne
avec des bornes dans l’ordre croissant, cela donne
![]()
Bilan :
![]()
3/ a/ Soit A>0,
![]()
Bilan : ![]()
3/ b/ Soit ![]() Soit
Soit ![]() On pose :
On pose :
![]() Les fonctions
Les fonctions ![]() sont
sont ![]() sur
sur ![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_0^{A}\frac{1}{(1+t^2)^n}\hbox{d}t &=&\left[\frac{t}{(1+t^2)^n}\right]_0^A-\int_0^{A}\frac{-2nt^2}{(1+t^2)^{n+1}}\hbox{d}t \\&=& \frac{A}{(1+A^2)^n}+2n\int_0^{A}\frac{(t^2+1)-1}{(1+t^2)^{n+1}}\hbox{d}t \\&=&\frac{A}{(1+A^2)^n}+2n\int_0^{A}\frac{1}{(1+t^2)^{n}}\hbox{d}t-2n\int_0^{A}\frac{1}{(1+t^2)^{n+1}}\hbox{d}t. \\ \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f3dcdc44288343340c395525ee246b5e_l3.png)
On a ![]() car
car ![]()
De sorte que, par passage à la limite, ![]()
Bilan : ![]()
On développe et ![]() donc
donc ![]() donc
donc
![]()
3/ c/
function H=emlyon17(n)
H=pi/2
for k=2:n ( H vaut H(k-1) )
H=(2*(k-1)-1)*H/(2*(k-1)) // H vaut (2*(k-1)-1)*H(k-1)/(2*(k-1))=H(k)
end ( en sortie H vaut H(n) car la dernière valeur de k est n )
endfunction
3/ d/ On pose : 
![]() Au rang 1,
Au rang 1, 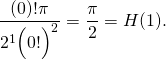 Donc
Donc ![]() est vraie.
est vraie.
![]() Supposons
Supposons ![]() pour un
pour un ![]() on a
on a
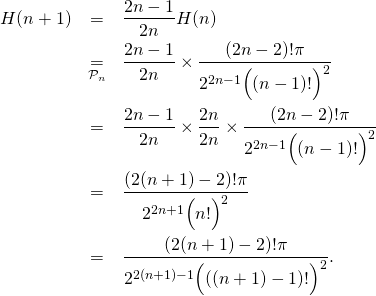
Donc ![]() est vraie.
est vraie.
Bilan :
![]()
Partie II : Étude de  lorsque
lorsque  tend vers
tend vers 
4/ a/ La fonction sinus hyperbolique ![]() est une combinaison linéaire d’exponentielles de polynômes donc elle est dérivable sur
est une combinaison linéaire d’exponentielles de polynômes donc elle est dérivable sur ![]() et
et
![]()
Donc ![]() est continue, strictement croissante sur
est continue, strictement croissante sur ![]() donc elle est une bijection de
donc elle est une bijection de ![]() vers
vers ![]()
Il est facile de voir que ![]()
Bilan :
![]()
Par réciprocité comme ![]() , on a
, on a ![]() et comme
et comme ![]() on a
on a ![]()
4/ b/ Soit ![]() Le changement de variables
Le changement de variables ![]() est de classe
est de classe ![]() sur
sur ![]()
On l’applique sur ![]() avec
avec ![]()
Ainsi
![]()
![]()
![]()
On peut faire tendre ![]() vers
vers ![]() dans l’égalité
dans l’égalité
![]()
Bilan :
![]()
5/ a/ Soit ![]() car
car ![]()
Comme ![]() est positif, on a
est positif, on a ![]() donc
donc ![]() .
.
Bilan :
![]()
5/ b/ La fonction inverse est décroissante sur ![]() donc, pour tout
donc, pour tout ![]()
![]()
Soit ![]() on a
on a ![]() donc la fonction
donc la fonction ![]() est croissante sur
est croissante sur ![]() donc
donc
![]()
On multiplie par ![]() et on intègre selon
et on intègre selon ![]() sur
sur ![]() avec des bornes dans l’ordre croissant.
avec des bornes dans l’ordre croissant.
Or ![Rendered by QuickLaTeX.com \displaystyle\int_0^{A}e^{-u(2x-1)}\hbox{d} u=\left[\frac{e^{-u(2x-1)}}{-(2x-1)}\right]_0^A=\frac{e^{-A(2x-1)}-1}{-(2x-1)}\underset{A\to +\infty}{\to}\frac{1}{2x-1}.](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-500228f702e5b3790307f9cf02cdae38_l3.png)
Par conséquent
![]()
Bilan :
![Rendered by QuickLaTeX.com \[\boxed{\text{ $\displaystyle \forall x\in I,\; \frac{1}{2x-1}\leqslant H(x)\leqslant \frac{4^x}{2(2x-1)}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c9aa4d86b1b9e4d5c831da6951827e6e_l3.png)
6/ On a ![]() (par valeurs positives) donc
(par valeurs positives) donc ![]() Donc par minoration
Donc par minoration ![]()
Avec ![]() et
et ![]() on a aussi
on a aussi ![]()
Dons par théorème des gendarmes ![]()
Bilan :
![Rendered by QuickLaTeX.com \[\boxed{\text{$H(x)\underset{(\frac12)^+}{\sim}\frac{1}{2x-1}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7287e5d67895c38c59da1d5f68b3c0a9_l3.png)
Partie III : Étude de  lorsque
lorsque  tend vers
tend vers 
7/ a/ On pose ![]() comme
comme ![]() la fonction
la fonction ![]() est
est ![]() sur
sur ![]() .
.
Soit ![]() on peut appliquer l’égalité des accroissements finis sur
on peut appliquer l’égalité des accroissements finis sur ![]() . Et il existe
. Et il existe ![]() tel que
tel que ![]() or
or ![]() donc
donc ![]() et
et ![]() donc avec
donc avec ![]() positif on a
positif on a ![]()
Pour ![]()
7/ b/ On rappelle que pour ![]() une densité de loi
une densité de loi ![]() est
est
![]()
Ici on pose ![]() On obtient
On obtient ![]() .
.
Comme l’intégrale sur ![]() de
de ![]() vaut 1,
vaut 1, ![]() converge et vaut
converge et vaut ![]()
Par parité de ![]()
![]() converge et vaut
converge et vaut
![Rendered by QuickLaTeX.com \[\boxed{\text{$\displaystyle\frac12\times \sqrt {\frac{2\pi}{x}}=\sqrt {\frac{\pi}{2x}}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c1ef0fef5758ab797fec08ff4611e0fa_l3.png)
7/ c/ Soit ![]() avec la question 7.a. avec
avec la question 7.a. avec ![]() . On intègre de 0 à 1 avec
. On intègre de 0 à 1 avec ![]() selon
selon ![]() ces fonctions continues,
ces fonctions continues,
![Rendered by QuickLaTeX.com \[0\leqslant \int_0^{1}\frac{1}{(1+t^2)^x}\hbox{d}t\leqslant \int_0^{1}e^{-xt^2/2}\hbox{d}t\leqslant \int_0^{1}e^{-xt^2/2}\hbox{d}t+\underset{\geqslant 0}{\underbrace{\int_1^{+\infty}e^{-xt^2/2}\hbox{d}t}}=\sqrt{\frac{\pi}{2x}}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9fbd78631f2dbf6244961987129109d9_l3.png)
7/ d/ Soit ![]() on a
on a ![]() donc
donc ![]() on compose par la fonction
on compose par la fonction ![]() croissante sur
croissante sur ![]() puis on intègre selon
puis on intègre selon ![]() sur
sur ![]() avec des bornes dans l’ordre croissant. On peut le faire car on a reconnu une intégrale de Riemann convergente avec
avec des bornes dans l’ordre croissant. On peut le faire car on a reconnu une intégrale de Riemann convergente avec ![]() Ainsi
Ainsi
![]()
Bilan :
![Rendered by QuickLaTeX.com \[\boxed{\text{$\displaystyle\forall x\in I,\; 0\leqslant \int_1^{+\infty}\frac{1}{(1+t^2)^x}\hbox{d}t\leqslant\frac{1}{2x-1}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c596ab18015278970aab19799d0feb6b_l3.png)
7/ e/ Il est clair que ![]() et
et ![]() donc par encadrement
donc par encadrement ![]() et
et ![]() .
.
Puis par somme de limites et relation de Chasles pour les intégrales convergentes,
![]()
8/ On note, pour tout ![]()
a/ Soit ![]() ,
,
![]()
![Rendered by QuickLaTeX.com \[=\underset{\hbox{Avec la question 3.b.}}{\underbrace{\ln\left(\frac{2n-1}{2n}\right)}}+\dfrac12\ln\left(1+\frac{1}{n}\right)=\ln\left(1-\frac{1}{2n}\right)+\frac12\ln\left(1+\frac{1}{n}\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a30d6c2e61528943e8410d764db05b29_l3.png)
On utilise ![]() on peut le faire car
on peut le faire car ![]()
Ainsi ![]()
On en déduit que
![]()
b/ On a ![]() Or la série de Riemann
Or la série de Riemann ![]() converge avec
converge avec ![]() Donc par comparaison des séries à terme général positif, la série
Donc par comparaison des séries à terme général positif, la série ![]() converge donc
converge donc ![]() converge.
converge.
Bilan :
![Rendered by QuickLaTeX.com \[\boxed{\text{la s\'erie $\displaystyle\sum_{n\geqslant 1}(u_{n+1}-u_n)$ converge.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-298ee5251075e1a326324d091d53af70_l3.png)
c/ Une série converge si et seulement si ses sommes partielles convergent or, pour tout ![]()
![Rendered by QuickLaTeX.com \[\sum_{n=1}^N(u_{n+1}-u_n)=u_{N+1}-u_1 \hbox{ par t\'elescopage.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2c6f3b7beca301283e1b16560740f0d6_l3.png)
Notons ![]() la somme de
la somme de ![]() , on a alors
, on a alors ![]() donc la suite
donc la suite ![]() converge. On note
converge. On note ![]() sa limite, donc la suite
sa limite, donc la suite ![]() converge, on note
converge, on note ![]() sa limite, elle est strictement positive. Or
sa limite, elle est strictement positive. Or ![]() en composant par exponentielle. Donc
en composant par exponentielle. Donc ![]() car
car ![]() non nul.
non nul.
Bilan :
![Rendered by QuickLaTeX.com \[\boxed{\text{$\displaystyle H(n)\underset{n\to +\infty}{\sim}\frac{K}{\sqrt{n}}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-546159f9d0fa4d9bad798abf92101977_l3.png)
9/ On a ![]() donc
donc ![]() Pour tout
Pour tout ![]() , on a
, on a ![]() et
et ![]() est décroissante donc
est décroissante donc ![]()
On multiplie par ![]() et
et
![]()
Donc
![]()
Comme ![]() on a
on a ![]()
Ainsi par encadrement ![]() car
car ![]() .
.
En effet ![]()
Partie IV : Étude d’une suite de variables aléatoires
10/ ![]() est définie sur
est définie sur ![]() elle y est positive, elle est continue sur
elle y est positive, elle est continue sur ![]() et sur
et sur ![]() Comme
Comme ![]() est nulle sur
est nulle sur ![]() on a :
on a :
![]() .
.
Donc ![]() converge et vaut 1.
converge et vaut 1.
Bilan :
![]()
11/ On considère une variable aléatoire ![]() à densité, de densité
à densité, de densité ![]()
a/ Soit ![]()
![]() car
car ![]() nulle sur
nulle sur ![]() .
.
Soit ![]()
![]()
b/ ![]() a pour densité
a pour densité ![]() donc
donc ![]() a une espérance si et seulement si l’intégrale
a une espérance si et seulement si l’intégrale ![]() converge.
converge.
Or ![]() et la fonction
et la fonction ![]() est positive sur
est positive sur ![]()
Comme l’intégrale ![]() diverge,
diverge, ![]() n’a pas d’espérance.
n’a pas d’espérance.
12/ On considère une suite de variables aléatoires réelles ![]() à densité, à valeurs strictement positives, mutuellement indépendantes, dont chacune a pour densité
à densité, à valeurs strictement positives, mutuellement indépendantes, dont chacune a pour densité ![]()
On définit, pour tout ![]() les variables aléatoires\quad
les variables aléatoires\quad ![]() et
et ![]()
a/ Soit ![]() de
de ![]() comme les
comme les ![]() sont à valeurs strictement positives, on a
sont à valeurs strictement positives, on a ![]() donc
donc ![]()
Soit ![]()
![]() est réalisé si et seulement si, pour tout
est réalisé si et seulement si, pour tout ![]() est réalisé. Donc
est réalisé. Donc
![Rendered by QuickLaTeX.com \[[M_n\leqslant x]=\bigcap\limits_{k=1}^n[X_k\leqslant x].\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9c8462ed28cebb51dd922bba8eb8d949_l3.png)
Par indépendance mutuelle des ![]() on obtient
on obtient
![Rendered by QuickLaTeX.com \[\hbox{P}\left(M_n\leqslant x\right)=\prod\limits_{k=1}^n\hbox{P}(X_k\leqslant x)=\left(F_X(x)\right)^n\hbox{ car il y a $n$ facteurs dans le produit}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9fedae80aba4248f06a180c0035c0764_l3.png)
Bilan :
![]()
b/ On pose ![]() La fonction inverse est dérivable sur
La fonction inverse est dérivable sur ![]() et
et ![]() est dérivable sur
est dérivable sur ![]() Donc par composition
Donc par composition ![]() est dérivable sur
est dérivable sur ![]() .
.
Par somme, ![]() est dérivable sur
est dérivable sur ![]() et, pour tout
et, pour tout ![]()
![]()
Donc la fonction ![]() est constante sur l’intervalle
est constante sur l’intervalle ![]()
Or ![]()
Finalement :
![Rendered by QuickLaTeX.com \[\boxed{\text{$\displaystyle\forall u\in ]0;+\infty[, \hbox{Arctan}(u)+\hbox{Arctan}\left(\frac1u\right)=\frac{\pi}{2}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2752a6ce4d8a8d9faa759f6314c48096_l3.png)
c/ Pour tout ![]() de
de ![]()
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} \hbox{P}(Z_n\leqslant x)&=&\displaystyle \hbox{P}\left(\frac{n}{M_n}\leqslant x\right)\\&=& \displaystyle \hbox{P}\left(\frac{n}{x}\leqslant M_n\right)\hbox{ avec $x>0$ et $M_n$ forc\'ement strictement positif}\\&=&\displaystyle1-\hbox{P}\left( M_n\leqslant\frac{n}{x}\right)\hbox{ sachant que $M_n$ est \`a densit\'e}\\&=&\displaystyle1-F_{M_n}\left( \frac{n}{x}\right)\\ &=&\displaystyle1-\left(\frac{2}{\pi}\hbox{Arctan}\left(\frac{n}{x}\right)\right)^n\hbox{ car $\frac{n}{x}>0$}\\ &=&\displaystyle 1-\left(1-\frac2{\pi}\hbox{Arctan}\left(\frac{x}{n}\right)\right)^n\hbox{ car si $u>0,$ alors $\hbox{Arctan}(u)+\hbox{Arctan}\left(\frac1u\right)=\frac{\pi}{2}$}\\ \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-820a7dd1d1be223a2206ce5184c98d20_l3.png)
donc ![]()
d/ Pour tout ![]() de
de ![]() on sait que
on sait que ![]() donc
donc ![]()
et ![]() donc on pourra composer par
donc on pourra composer par ![]()
Par conséquent ![]()
On sait que ![]() car
car ![]() donc avec
donc avec ![]() on a
on a
![]() car
car ![]() et
et ![]()
On en déduit que ![]() donc, sachant que
donc, sachant que ![]() est indépendant de
est indépendant de ![]() on a
on a
![]()
On peut composer cette limite par exponentielle qui est continue en ![]()
Donc ![]()
On en déduit que
![]()
On reconnait la fonction de répartition d’une loi exponentielle de paramètre ![]()
Bilan : la suite de variables aléatoires ![]() converge en loi vers une variable suivant une loi exponentielle de paramètre
converge en loi vers une variable suivant une loi exponentielle de paramètre ![]()

