Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EM Lyon Maths ECS 2018
Revenir à tous les corrigés des annales maths BCE
Problème I. Suite d’intégrales et équivalent
Partie I : Étude d’une suite d’intégrales
1/ On a
![Rendered by QuickLaTeX.com \begin{eqnarray*} W_{0} &=&\int_{0}^{\frac{\pi }{2}}1du=\pi /2 \\ W_{1} &=&\int_{0}^{\frac{\pi }{2}}\sin (u)du=\left[ -\cos \left( u\right) \right] _{0}^{\pi /2}=1 \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8f0600dc3923f272e2df791c6e28a1b1_l3.png)
Donc ![]() et
et ![]()
2/ Soit ![]() . Puisque l’on ne doit plus avoir qu’une seule intégrale, on les regroupe (linéarité) :
. Puisque l’on ne doit plus avoir qu’une seule intégrale, on les regroupe (linéarité) :
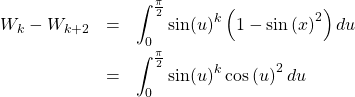
et pour pouvoir trouver la primitive la puissance, on la regroupe avec sa dérivée
![]()
![]()
et ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() donc
donc
![Rendered by QuickLaTeX.com \begin{eqnarray*} W_{k}-W_{k+2} &=&\left[ \cos \left( u\right) \frac{1}{k+1}\sin \left( u\right) ^{k+1}\right] _{0}^{\pi /2}-\int_{0}^{\frac{\pi }{2}}-\sin \left( u\right) \frac{1}{k+1}\sin \left( u\right) ^{k+1}du \\ &=&0+\frac{1}{k+1}\int_{0}^{\frac{\pi }{2}}-\sin \left( u\right) \sin \left( u\right) ^{k+1}du=\frac{1}{k+1}W_{k+2} \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ec9d3e10f2c39a819c2aa4b58a63202f_l3.png)
et on a donc bien ![]()
Partie II : Une autre expression de 
3/ On doit montrer que ![]() par le changement de variable
par le changement de variable ![]()
![]() est continue sur
est continue sur ![]()
![]()
![]() est une bijection croissante et de classe
est une bijection croissante et de classe ![]() de
de ![]() sur
sur ![]()
Donc, les deux intégrales sont de même nature ![]()
Comme ![]() converge, alors
converge, alors ![]() converge et
converge et ![]() .
.
4/ ![]() intégrale impropre en
intégrale impropre en ![]() car
car ![]() continue
continue ![]()
a/ Quand ![]() donc
donc ![]()
avec ![]() constante par rapport à
constante par rapport à ![]()
Or, ![]() converge donc, par équivalence de fonctions positives,
converge donc, par équivalence de fonctions positives, ![]() converge également.
converge également.
Donc ![]() est définie sur
est définie sur ![]()
Pour tout ![]()
![]() et
et ![]()
Donc ![]() est paire.
est paire.
b/ On a ![]() .
.
5/ Soit ![]() .
.
a/ Soient ![]() et
et ![]() .
.
![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]()
Pour ![]() donc
donc ![]() et
et ![]() car
car ![]()
Donc (Taylor-Lagrange à l’ordre ![]() appliquée à la fonction entre
appliquée à la fonction entre ![]() et
et ![]()
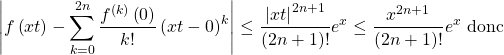
de même quand ![]() est impair,
est impair, ![]() et pour
et pour ![]() pair
pair ![]() donc
donc
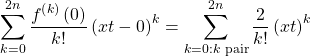
réindexé par ![]() on obtient
on obtient ![]() }
}![]()
b/ On reconstruit alors l’inégalité sur ![]() pour tout
pour tout ![]()
![]()
avec les bornes croissantes
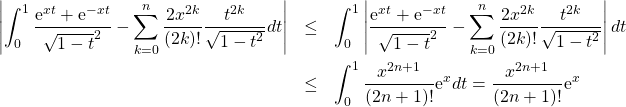
finalement
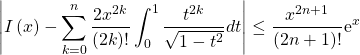
et, pour tout ![]() de
de ![]() :
: 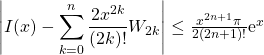 .
.
c/ Quand ![]() tend vers
tend vers ![]()
![]() (
(![]() est constante)
est constante)
Donc ![]() et
et ![]()
et ![]()
Finalement, 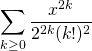 converge et
converge et 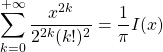 .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie III : Équivalent de  lorsque
lorsque  tend vers
tend vers 
6/ On sait que ![]()
On doit donc comparer deux intégrales et pour cela comparer leurs contenus :
Pour tout ![]() donc, pour
donc, pour ![]() et (bornes croissantes).
et (bornes croissantes).
Or, pour tout ![]() de
de ![]() :
: ![]() .
.
7/ a/ Pour tout ![]()
et
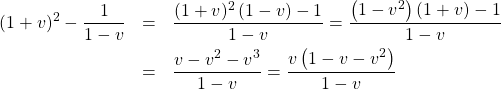
![]() peut se traiter comme polynôme du second degré.
peut se traiter comme polynôme du second degré.
Plus simplement ici : ![]() donc
donc ![]() et
et ![]() donc
donc ![]() et
et![]()
Finalement, pour tout ![]() de
de ![]() :
: ![]() .
.
7/ b/ Soit ![]() .
.
![]() et
et ![]() converge.
converge.
Donc par équivalence de fonctions positives, ![]() converge.
converge.
Changement de variable ![]() (forme que l’on pourrait changer en
(forme que l’on pourrait changer en ![]() mais ce sens nous est imposé par l’énoncé).
mais ce sens nous est imposé par l’énoncé).
On doit donc préparer le terrain avant d’intervenir. On prépare le terrain :
![]() et
et ![]()
![]()
![]() est continue sur
est continue sur ![]()
![]() est une bijection décroissante et de classe
est une bijection décroissante et de classe ![]() de
de ![]() dans
dans ![]() et
et ![]()
donc les intégrales sont de même nature (convergentes) et
![]()
donc ![]()
![]()
7/ c/ Pour tout ![]() de
de ![]()
On a pour tout ![]() de
de ![]() :
: ![]()
Or, pour ![]() donc
donc ![]() et
et ![]()
multiplié par ![]() :
:
![]()
avec les bornes croissantes
![]()
en développant la troisième intégrale
![]()
8/ a/ Une densité de la loi normale d’espérance nulle et de variance ![]() est
est ![]()
![]()
Avec ![]() on a
on a ![]()
Donc ![]() converge et vaut
converge et vaut ![]()
Sa variance est ![]() donc
donc ![]() (converge)
(converge)
Et, par parité ![]() .
.
8/ b/ Soit ![]() . À l’aide du changement de variable
. À l’aide du changement de variable ![]() ,
,
![]() est une bijection croissante et
est une bijection croissante et ![]() de
de ![]() dans
dans ![]() et
et ![]()
On a :
![]() avec
avec ![]() continue sur
continue sur ![]()
Donc
![]()
et ![]() quand
quand ![]() donc
donc ![]() et par produit
et par produit
![]()
De même :

et ![]() donc
donc
![]()
et on a donc bien ![]() et
et ![]()
9/ On a
![]()
La seconde intégrale est bornée puisque ![]()
La première a été encadrée avec
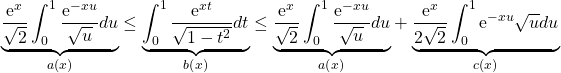
avec ![]()
et ![]() donc
donc ![]() on a donc
on a donc
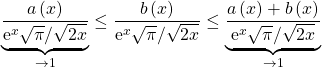
et par encadrement, ![]() quand
quand ![]() , donc
, donc ![]()
Partie IV : Une application en probabilités
10/ a/ Pour estimer ![]() on prend comme estimateur la moyenne statistique des réalisations de cet événement :
on prend comme estimateur la moyenne statistique des réalisations de cet événement :
On réalise ![]() fois une double simulation de Poisson dont on teste l’égalité.
fois une double simulation de Poisson dont on teste l’égalité.
Un compteur ![]() totalise les occurences.
totalise les occurences.
function r = estime(lambda);
n=1000;cpt=0
for i=1:n
if ( grand(1,1,’poi’,lambda)==grand(1,1,’poi’,lambda) ) then cpt=cpt+1
r=cpt/n
endfunction
On peut également générer une liste de réalisations de X et de Y puis créer la liste des X==Y et enfin dénombrer les ![]() (true, vrai)
(true, vrai)
La valeur ![]() est vue par Scilab comme
est vue par Scilab comme ![]() . sum([
. sum([![]() ,
,![]() ,
,![]() ])=2
])=2
function ![]() r = estime(lambda);
r = estime(lambda);
n=1000;cpt=0
X=grand(1,n,’poi’,lambda) \#
X=grand(1,n,’poi’,lambda)
r=sum(X==Y)/n
endfunction
11/ Grâce à la fonction précédente, on trace, en fonction de ![]() , une estimation de
, une estimation de ![]() pour
pour ![]() et on obtient le graphe suivant :
et on obtient le graphe suivant :

![]() semble donc tendre vers
semble donc tendre vers ![]()
Donc ![]() tend vers
tend vers ![]() et
et ![]() quand
quand ![]() tend vers
tend vers ![]()
![]()
Pour réaliser ce graphique, on peut procéder ainsi :
lambda=linspace(0,20,100)
Y=zeros(1,100)
for i=1:100
Y(i)=estime(lambda(i))*sqrt(\pi*lambda(i))
end
plot2d(lambda,Y)
12/ a/ On a ![]()
![]() réunion d’incompatibles donc
réunion d’incompatibles donc
![]() et comme
et comme ![]() et
et ![]() sont indépendantes,
sont indépendantes,
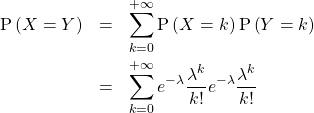
avec ![]() constante par rapport à
constante par rapport à ![]() donc
donc ![Rendered by QuickLaTeX.com \mathrm{P}([X=Y])=\mathrm{e}^{-2\lambda }\displaystyle \sum_{k=0}^{+\infty }\frac{\lambda ^{2k}}{(k!)^{2}}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7403af846ae8091c0c4bf191da81f7b2_l3.png) .
.
12/ a/ On se souvient que ![]() pour
pour ![]() .
.
On ajuste avec ![]() donc
donc ![]()
![]() .
.
b/ Et comme ![]() en substituant
en substituant ![]() on a
on a
![]() lorsque
lorsque ![]() tend vers
tend vers ![]() .
.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Problème 2 : Algèbre linéaire et suite de variables aléatoires
Partie I :
1/ a/ Pour tout ![]()
![]() donc
donc ![]() est bien définie.
est bien définie.
Soient ![]() et
et ![]() , alors :
, alors :
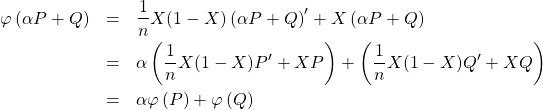
Donc ![]() est une application linéaire.
est une application linéaire.
b/ ![]()
c/ Et si ![]() alors
alors ![]()
Donc si ![]() il existe
il existe ![]() et
et ![]() tel que
tel que ![]()
et ![]() donc
donc ![]() et
et ![]()
Donc ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
2/ Pour ![]()
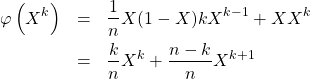
et ![]() donc
donc 
C’est une matrice échelonnée donc le rang est égal au nombre de pivots :
![]()
3/ a/ Comme ![]()
![]() (théorème du rang)
(théorème du rang)
Donc ![]() et
et ![]() n’est pas injejctif
n’est pas injejctif
b/ Soit ![]() un polynôme non nul de
un polynôme non nul de ![]() .
.
On a alors![]() (polynôme nul)
(polynôme nul)
Donc ![]()
En particulier, en ![]()
Donc ![]()
![]() Si
Si ![]() est racine de
est racine de ![]() alors
alors ![]() donc
donc ![]()
Donc ![]() est racine d’ordre 2 de
est racine d’ordre 2 de ![]() donc de
donc de ![]()
Et pour tout entier ![]() (récurrence)
(récurrence) ![]() sera racine d’ordre
sera racine d’ordre ![]()
Donc ![]() est le polynôme nul. Ce qui est faux.
est le polynôme nul. Ce qui est faux.
Donc ![]()
![]() Si
Si ![]() alors il existe
alors il existe ![]() de degré
de degré![]() et
et ![]() tel que
tel que ![]() et
et ![]()
Et comme ![]() alors
alors ![]() et
et ![]()
Donc ![]()
![]()
Donc ![]() est une famille libre (un vecteur non nul) de
est une famille libre (un vecteur non nul) de ![]() vecteur de
vecteur de ![]() et
et ![]() donc
donc ![]() est une base du noyau.
est une base du noyau.
Donc, ![]() et les polynômes du noyau sont des polynômes de degré
et les polynômes du noyau sont des polynômes de degré ![]() qui ont
qui ont ![]() pour seule racine.
pour seule racine.
c/ Le noyau étant de dimension ![]() il suffit de trouver un vecteur non nul du noyau pour avoir une base.
il suffit de trouver un vecteur non nul du noyau pour avoir une base.
Ce polynôme n’a que ![]() comme racine. Sa décomposition en éléments simples est donc de la forme
comme racine. Sa décomposition en éléments simples est donc de la forme ![]()
Et comme il est de degré ![]() , c’est
, c’est ![]()
4/ ![]() est triangulaire. Ses valeurs propres sont sur la diagonale.
est triangulaire. Ses valeurs propres sont sur la diagonale.
Donc ![]() a
a ![]() valeurs propres distinctes. Et
valeurs propres distinctes. Et ![]() est diagonalisable.
est diagonalisable.
5/ On pose, pour tout ![]() de
de ![]() :
: ![]() .
.
a/ On se doute que ![]() va être vecteur propre. On cherche donc à faire réapparaître une forme factorisée
va être vecteur propre. On cherche donc à faire réapparaître une forme factorisée
Pour tout ![]() de
de ![]() ,
, ![]() (nulle pour
(nulle pour ![]() )
)
![Rendered by QuickLaTeX.com \begin{eqnarray*} \varphi (P_{k}) &=&\frac{1}{n}X\left( 1-X\right) \left[ kX^{k-1}\left( 1-X\right) ^{n-k}-\left( n-k\right) X^{k}\left( 1-X\right) ^{n-k-1}\right] +XX^{k}(1-X)^{n-k} \\ &=&X^{k}(1-X)^{n-k}\left[ \frac{k}{n}\left( 1-X\right) -\frac{n-k}{n}X+X \right] \\ &=&\frac{k}{n}P_{k} \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-768a7f8c9b09f29f7b63d4b42c5bdc83_l3.png)
Ce qui est vrai encore pour ![]() et
et ![]()
b/ Donc ![]() est un vecteur propre associé à la valeur propre
est un vecteur propre associé à la valeur propre ![]() .
.
Les valeurs propres étant distinctes, la famille ![]() est libre.
est libre.
C’est une famille libre de ![]() vecteurs de
vecteurs de ![]() et
et ![]()
Donc ![]() est une base de
est une base de ![]() et la matrice de
et la matrice de ![]() dans cette base est
dans cette base est

c/ On a ici ![]() valeurs propres distinctes.
valeurs propres distinctes.
Il n’y en a donc pas d’autres.
Les sous espaces propres de ![]() sont donc
sont donc ![]() pour
pour ![]()
Partie II : Étude d’une suite de variables aléatoires
6/ a/ ![]()
![]() signifie qu’au second tirage, on n’obtient pas de nouveau numéro, c’est à dire que l’on retire le même numéro qu’au premier.
signifie qu’au second tirage, on n’obtient pas de nouveau numéro, c’est à dire que l’on retire le même numéro qu’au premier.
Donc ![]() car les
car les ![]() boules sont équiprobables.
boules sont équiprobables.
d’où ![]() .
.
b/ Soit ![]() . Pour tout
. Pour tout ![]() de
de ![]() , si
, si ![]() on a déjà obtenus
on a déjà obtenus ![]() numéros. Et il y en a donc
numéros. Et il y en a donc ![]() que l’on a pas obtenus.
que l’on a pas obtenus.
La probabilité d’obtenir un de ceux ci est donc ![]()
Comme, en ![]() tirages on peut obtenir entre
tirages on peut obtenir entre ![]() et
et ![]() numéros distincts,
numéros distincts, ![]() est un système complet d’événements de probabilités non nulle et
est un système complet d’événements de probabilités non nulle et
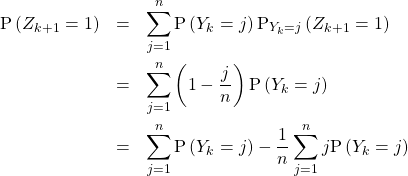
donc ![]() .
.
c/ Soit ![]() .
. ![]() compte le nombre de numéro rajouté lors du
compte le nombre de numéro rajouté lors du ![]() tirage (
tirage (![]() ou
ou ![]() )
)
Donc, ![]() est le nombre total de numéros ajouté en
est le nombre total de numéros ajouté en ![]() tirage. Et en partant de
tirage. Et en partant de ![]() ,
, 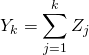
Donc ![]() et comme
et comme ![]() suit une loi de Bernouilli,
suit une loi de Bernouilli, ![]() d’où :
d’où :
![]() }
}
d/ D’où une récurrence avec prédécesseurs puisque l’on utilise tous les termes précédents :
![]()
Soit ![]() tel que, pour tout
tel que, pour tout ![]() alors
alors
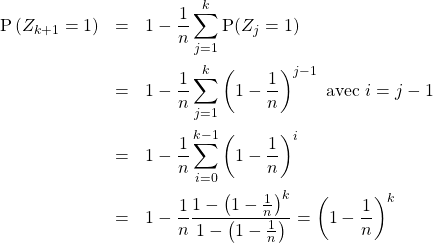
Donc, pour tout ![]() de
de ![]() :
: ![]() .
.
e/ Comme ![]() on a donc
on a donc ![]()
et ![]()
7/ On note, pour tout ![]() de
de ![]() ,
, ![]() le polynôme de
le polynôme de ![]() défini par :
défini par :
![]()
(appelée fonction génératrice de ![]() )
)
a/ On a ![]() car
car ![]() pour
pour ![]()
![]()
![]() car
car ![]()
![]()
![]() signifie que l’on a eu le même numéro aux deux tirages donc que l’on n’a pas de nouveau numéro au second.
signifie que l’on a eu le même numéro aux deux tirages donc que l’on n’a pas de nouveau numéro au second.
![]()
et ![]()
![]()
et ![]()
donc ![]() .
.
b/ Pour tout ![]() de
de ![]() et tout
et tout ![]() de
de ![]() :
:
![]() si l’on a obtenus
si l’on a obtenus ![]() numéros distincts au
numéros distincts au ![]() tirage.
tirage.
Cela arrive ou bien quand on en a eu un de plus au ![]() et un de moins avant (
et un de moins avant (![]() , ou bien quand on n’en a pas eu un de plus et qu’on avait déjà eu
, ou bien quand on n’en a pas eu un de plus et qu’on avait déjà eu ![]() numéros avant.
numéros avant.
Donc ![]()
C’est une réunion d’évènements incompatibles donc ![]()
avec ![]() et
et ![]()
donc ![]()
c/ On a :
![Rendered by QuickLaTeX.com \begin{eqnarray*} G_{k+1} &=&\sum_{i=0}^{n}\mathrm{P}\left( Y_{k+1}=i\right) X^{i} \\ &=&\sum_{i=0}^{n}\left[ \left( 1-\frac{i-1}{n}\right) \mathrm{P}\left( Y_{k}=i-1\right) +\frac{i}{n}\mathrm{P}\left( Y_{k}=i\right) \right] X^{i} \text{ r\'eindex\'e }j=i-1 \\ &=&\sum_{j=0}^{n}\mathrm{P}\left( Y_{k}=j\right) X^{j+1}-\frac{1}{n} \sum_{j=0}^{n}j\mathrm{P}\left( Y_{k}=j\right) X^{j+1}+\frac{1}{n} \sum_{i=0}^{n}i\mathrm{P}\left( Y_{k}=i\right) X^{i} \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a9f56c6a8f288670beb9533284583bd3_l3.png)
on fait alors apparaître la dérivée ![]()
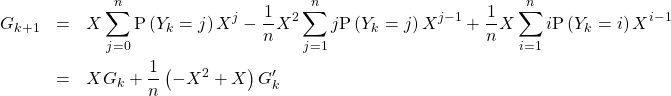
et on a bien ![]()
d/ On a montré que ![]() pour tout entier
pour tout entier ![]() relation « géométrique »
relation « géométrique »
![]() Pour
Pour ![]()
![]() Soit
Soit ![]() tel que
tel que ![]()
alors ![]()
Donc, pour tout ![]() de
de ![]() :
: ![]()
8/ a/ Pour tout ![]() de
de ![]() ,
, ![]() donc
donc ![]() et
et ![]() donc
donc ![]() et
et ![]()
b/ Pour tout ![]() de
de ![]() en reprenant la relation
en reprenant la relation ![]() , on redérive pour faire apparaître
, on redérive pour faire apparaître ![]()
On a :
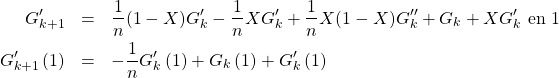
donc ![]()
c/ Avec ![]() on a ici une suite arithmético-géométrique.
on a ici une suite arithmético-géométrique.
Soit ![]()
Soit ![]()
On a alors ![]() géométrique et
géométrique et ![]() avec
avec ![]() .
.
On a donc ![]() et
et ![]() donc
donc ![]() ce qui est cohérent.
ce qui est cohérent.
9/ On rappelle que les polynômes ![]() sont définis à la question 5. par :
sont définis à la question 5. par :
![]()
a/ On a ![]() , ce qui donne les coordonnées de
, ce qui donne les coordonnées de ![]() dans la base
dans la base ![]()
b/ Pour tout ![]() de
de ![]() , en réindexant
, en réindexant ![]()
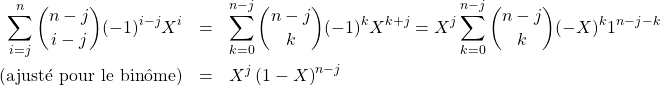
On a donc ![]()
c/ Et, pour tout ![]() de
de ![]() :
:
La matrice de ![]() dans la base
dans la base ![]() est diagonale, ce qui permet de calculer ses puissances.(ou bien, les
est diagonale, ce qui permet de calculer ses puissances.(ou bien, les ![]() sont des vecteurs propres de
sont des vecteurs propres de ![]() )
)
On décompose donc ![]() sur cette base.
sur cette base.
Question a) : ![]() donc
donc
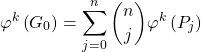
Or, ![]() est associé à la valeur propre
est associé à la valeur propre ![]() donc
donc ![]() et
et
![Rendered by QuickLaTeX.com \begin{equation*} \varphi ^{k}\left( G_{0}\right) =\sum_{j=0}^{n}\dbinom{n}{j}\left( \frac{j}{ n}\right) ^{k}P_{j}=\sum_{j=0}^{n}\left[ \dbinom{n}{j}\left( \frac{j}{n} \right) ^{k}\sum_{i=j}^{n}\dbinom{n-j}{i-j}(-1)^{i-j}X^{i}\right] \end{equation*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-db7524c26e1171aebe20796bea653818_l3.png)
avec ![]() et
et ![]() et
et ![]() donc
donc
![Rendered by QuickLaTeX.com \begin{equation*} \varphi ^{k}\left( G_{0}\right) =\sum_{i=0}^{n}\left[ \sum_{j=0}^{i}\dbinom{n }{j}\left( \frac{j}{n}\right) ^{k}\dbinom{n-j}{i-j}(-1)^{i-j}\right] X^{i} \end{equation*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-30dc30ac122f596cf0f4d098a12d7eaa_l3.png)
d/ Pour tout ![]() de
de ![]() et pour tout
et pour tout ![]() de
de ![]() :
:
![]()
Donc ![]() est la coordonnée sur
est la coordonnée sur ![]() dans la base canonique de
dans la base canonique de ![]()
Donc
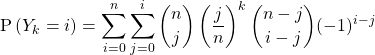
et il reste à transformer en factorielle les coefficients du binôme (valable car ![]() et
et ![]() )
)
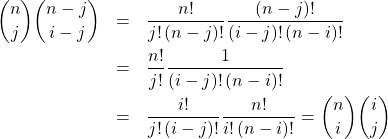
avec ![]() constant par rapport à
constant par rapport à ![]() donc
donc
![]()

