Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet ESSEC Maths ECS 2016
Revenir à tous les corrigés des annales maths BCE
Partie I :
1/ Soit ![]() . Pour tout
. Pour tout ![]() ,
, ![]() et on a
et on a
![]()
La série de terme général ![]() est une série de Riemann convergente. Donc la série de tg
est une série de Riemann convergente. Donc la série de tg ![]() est convergente. Par théorème de comparaison pour les séries à terme positif, la série de tg
est convergente. Par théorème de comparaison pour les séries à terme positif, la série de tg ![]() converge. La série de terme général
converge. La série de terme général ![]() est alors absolument convergente donc convergente.
est alors absolument convergente donc convergente.
2/ a/ Pour tout ![]() ,
, ![]() . De plus, pour tout
. De plus, pour tout ![]() ,
, ![]() .
.
On en déduit ![]() .
.
Or, ![]() . D’où
. D’où ![]() .
.
![]()
2/ b/ Soit ![]() et
et ![]() ,
,
![]()
2/ c/ Soit ![]() et
et ![]() . D’après l’égalité de la question 2.b,
. D’après l’égalité de la question 2.b,
![Rendered by QuickLaTeX.com \[\sum\limits_{n=1}^{N}u_n(x+1)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-28c7949d7bc33d073490193861ef8787_l3.png)
![Rendered by QuickLaTeX.com \[=\sum\limits_{n=1}^{N}\left[\frac{1}{n-1-x}-\frac{1}{n+1+x}\right]\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a6ce6b0e97057d2370cb6d34d49d80e8_l3.png)
![Rendered by QuickLaTeX.com \[=\sum\limits_{n=1}^{N}\frac{1}{n-1-x}-\sum\limits_{n=1}^{N}\frac{1}{n+1+x}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-07a935ba3bf79d3971525cd85bf444a9_l3.png)
On fait le changement d’indice ![]() dans la première somme et
dans la première somme et ![]() dans la seconde. On obtient
dans la seconde. On obtient
![Rendered by QuickLaTeX.com \[\sum\limits_{n=1}^{N}u_n(x+1)=\sum\limits_{k=0}^{N-1}\frac{1}{k-x}-\sum\limits_{k=2}^{N+1}\frac{1}{k+x}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0b88c2f12df4b8e0f2aabe1773658bba_l3.png)
D’où, ![]()
![]()
Ainsi, ![]()
![]() .
.
On fait tendre ![]() vers
vers ![]() car tout converge dans cette égalité. Il vient
car tout converge dans cette égalité. Il vient
![]()
![]()
Par suite
![]()
![]()
3/ a/ Soit ![]() . Pour tout
. Pour tout ![]() ,
, ![]() et
et ![]() d’après la question 2.b qui reste encore valable pour
d’après la question 2.b qui reste encore valable pour ![]() (de façon immédiate) et pour
(de façon immédiate) et pour ![]() car
car ![]() .
.
De même qu’à la question 1, la série de terme général ![]() (pour
(pour ![]() ) est absolument convergente donc convergente. On en déduit l’existence de
) est absolument convergente donc convergente. On en déduit l’existence de ![]() et on a
et on a
![Rendered by QuickLaTeX.com \[\fbox{\text{$g(x)=\sum\limits_{n=2}^{\infty}\frac{2x}{n^2-x^2}=\sum\limits_{n=2}^{\infty}\left(\frac{1}{n-x}-\frac{1}{n+x}\right)$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-768bc0bc4a8a450907370a9e710fc706_l3.png)
3/ b/ Soit ![]() .
.
![]()
car comme déjà vérifié précédemment, ![]() .
.
3/ c/ Soit ![]() et
et ![]() . Pour tout
. Pour tout ![]() ,
,
![]() et
et ![]()
D’où,
![]()
![]()
Pour tout ![]() , on a donc
, on a donc
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}\left|\sum\limits_{n=2}^{N}u_n(x+h)-\sum\limits_{n=2}^{N}u_n(x)\right|&\leq &\sum\limits_{n=2}^{N}|u_n(x+h)-u_n(x)|\\&\leq & |h|\sum\limits_{n=2}^{N}\left|\frac{1}{(n-x)(n-x-h)}+\frac{1}{(n+x)(n+x+h)}\right|\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f2f8e1131b48bea106b1fe151a68db9c_l3.png)
Or, pour tout ![]() , comme
, comme ![]() et
et ![]() ,
,
![]() et
et ![]()
Dès lors, ![]()
![]() et
et
![Rendered by QuickLaTeX.com \[\left|\sum\limits_{n=2}^{N}u_n(x+h)-\sum\limits_{n=2}^{N}u_n(x)\right|\leq |h|\sum\limits_{n=2}^{N}\frac{2}{(n-1)(n-\frac{3}{2})}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1df7db619d3623f98b6fdd6ed3a280f0_l3.png)
![]() .
.
La série de tg ![]() est le multiple du terme général d’une série de Riemann convergente.
est le multiple du terme général d’une série de Riemann convergente.
Par théorème de convergence pour séries à termes positifs, on en déduit que la série de tg ![]() converge. On peut alors faire tendre
converge. On peut alors faire tendre ![]() vers
vers ![]() dans l’inégalité précédente car toutes les quantités convergent. On obtient
dans l’inégalité précédente car toutes les quantités convergent. On obtient
![Rendered by QuickLaTeX.com \[|g(x+h)-g(x)|\leq |h|\sum\limits_{n=2}^{N}\frac{2}{(n-1)(n-\frac{3}{2})}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ecf1c0376d7fdcf75ddbfb28961eb24b_l3.png)
On a donc bien
![Rendered by QuickLaTeX.com \[\fbox{\text{$\forall x\in[{0},{1}] \: \:f |g(x+h)-g(x)|\leq C|h|$ avec $C=\sum\limits_{n=2}^{N}\frac{2}{(n-1)(n-\frac{3}{2})}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1c2c89a0cd153ec4207f1c5c030f6eab_l3.png)
3/ d/ Soit ![]() . D’après la question précédente, pour tout
. D’après la question précédente, pour tout ![]() ,
,
![]()
![]() . Par théorème d’encadrement,
. Par théorème d’encadrement, ![]() d’où
d’où ![]() . La fonction
. La fonction ![]() est donc continue en
est donc continue en ![]() . Cette propriété est vraie pour tout
. Cette propriété est vraie pour tout ![]() de
de ![]() .
.
![]()
D’après la question 3.b, pour tout ![]() ,
,
![]()
Les fonctions ![]() ,
, ![]() et
et ![]() sont continues sur
sont continues sur ![]() ainsi que la fonction
ainsi que la fonction ![]() . Par somme, on en déduit que la fonction
. Par somme, on en déduit que la fonction ![]() est continue sur
est continue sur ![]() .
.
Or, la fonction ![]() est périodique de période 1. Par suite,
est périodique de période 1. Par suite,
![]()
4/ a/ D’après la question 3.b, pour tout ![]() ,
, ![]() . Donc pour tout
. Donc pour tout ![]() ,
, ![]() .
.
D’après la question 3.d, ![]() donc
donc ![]() . De plus,
. De plus, ![]()
![]() et
et ![]()
![]() . Par théorème d’opérations,
. Par théorème d’opérations,
![]()
De plus, pour tout ![]() ,
, ![]() car
car ![]() est impaire (d’après la question I.2.a). Or, d’après le calcul précédent,
est impaire (d’après la question I.2.a). Or, d’après le calcul précédent, ![]() . D’où
. D’où
![]()
On en déduit ![]() puis
puis
![]()
Pour tout ![]() ,
, ![]() . On en déduit par théorème d’opération et par continuité de
. On en déduit par théorème d’opération et par continuité de ![]() sur
sur ![]()
![]()
Or, ![]() et
et ![]() . D’où
. D’où
![]()
Pour tout ![]() , on a
, on a
![]()
Or si ![]() ,
, ![]() donc
donc ![]() . D’où
. D’où ![]() . On a donc
. On a donc
![]()
4/ b/ Pour tout ![]() ,
, ![]() . Or,
. Or, ![]() . Donc d’après les résultats de la question précédente,
. Donc d’après les résultats de la question précédente, ![]() d’où
d’où
![]()
On a également d’après ce qui précède, pour ![]() ,
, ![]() . Ainsi,
. Ainsi,
![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie II :
5/ Soit ![]() . Pour tout
. Pour tout ![]() ,
, ![]() et
et ![]() . Par composition, la fonction
. Par composition, la fonction ![]() est encore continue sur
est encore continue sur ![]() et à valeurs réelles. Donc
et à valeurs réelles. Donc ![]() .
.
Soit ![]() et
et ![]() . Pour tout
. Pour tout ![]() ,
,
&=&(\lm f+g)\left(\frac{x}{2}\right)+(\lm f+g)\left(\frac{x+1}{2}\right)\\ &=&\lm \left(f\left(\frac{x}{2}\right)+f\left(\frac{x+1}{2}\right)\right)+g\left(\frac{x}{2}\right)+g\left(\frac{x+1}{2}\right) \\ &=& \lm[T(f)](x)+[T(g)](x) \\ \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cafe69683ca8d53fcbfabda071cfc5d2_l3.png)
On a donc ![]() et
et
![]()
6/ a/ Soit ![]() . Pour tout
. Pour tout ![]() ,
,
=\frac{x^k}{2^k}+\frac{(x+1)^k}{2^k}=\frac{1}{2^k}\left(2x^k+\sum\limits_{j=0}^{k-1} \binom{k}{j}x^j\right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-199e11ebce1b6578fef7a913d37c9832_l3.png)
On a donc ![]() .
.
Par linéarité de l’endomorphisme ![]() , la famille
, la famille ![]() étant une base de
étant une base de ![]() , on en déduit
, on en déduit
![]()
6/ b/ On reprend les calculs de la question précédente :
![Rendered by QuickLaTeX.com \[\forall k\in [\![{0},{n}]\!], \: T(e_k)=\frac{1}{2^k}\sum\limits_{j=0}^{k-1}\binom{k}{j}e_j+\frac{1}{2^{k-1}}e_k\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2288ac8003a544f43da0508ede4909ed_l3.png)
La matrice de ![]() dans
dans ![]() est donc triangulaire supérieure et
est donc triangulaire supérieure et
![Rendered by QuickLaTeX.com \[\fbox{\text{${\rm Mat}_{B_n}(T_n)=\begin{pmatrix}2&1/2&\cdots& 1/2^k&\cdots& 1/2^n\\0&1& \cdots& k/2^k& \cdots& n/2^n\\\vdots&\vdots& \ddots& \vdots& \vdots& \vdots\\\vdots&\vdots& \vdots& 1/2^{k-1}&\cdots& \binom{n}{k}/2^n\\\vdots&\vdots& \ddots& \vdots& \ddots& \vdots\\0 & \cdots& \cdots& \cdots& 0 & 1/2^{n-1}\\\end{pmatrix}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3806d3e29c7a7d665ccd4da72fab19e0_l3.png)
6/ c/ La matrice de ![]() dans la base
dans la base ![]() est triangulaire supérieure. On en déduit directement les valeurs propres de
est triangulaire supérieure. On en déduit directement les valeurs propres de ![]() qui sont les éléments diagonaux. Les valeurs propres de
qui sont les éléments diagonaux. Les valeurs propres de ![]() sont donc les
sont donc les
![]()
![]() est un endomorphisme de
est un endomorphisme de ![]() qui est de dimension
qui est de dimension ![]() . De plus,
. De plus, ![]() a
a ![]() valeurs propres distinctes deux à deux. On en déduit que
valeurs propres distinctes deux à deux. On en déduit que
![]()
7/ a/ D’après la question 6, on a ![]() donc
donc ![]() . Par conséquent,
. Par conséquent,
![]()
7/ b/ Comme ![]() est dans
est dans ![]() , pour tout
, pour tout ![]() ,
,
![]()
En appliquant cette égalité à ![]() , on obtient
, on obtient
![]() d’où
d’où ![]()
Or ![]() étant le minimum de
étant le minimum de ![]() sur
sur ![]() , on a
, on a ![]() d’où
d’où
![]()
Or ![]() . On en déduit
. On en déduit
![]()
7/ c/ Montrons par récurrence que pour tout ![]() ,
, ![]() .
.
![]() L’égalité est immédiate par définition pour
L’égalité est immédiate par définition pour ![]() .
.
![]() Soit
Soit ![]() . Supposons
. Supposons ![]() . On applique alors le résultat de la question 7.b à
. On applique alors le résultat de la question 7.b à ![]() qui vérifie bien l’égalité demandée. On obtient ainsi
qui vérifie bien l’égalité demandée. On obtient ainsi
![]() d’où
d’où ![]()
Par conséquent,
![]()
7/ d/ La fonction ![]() est continue sur
est continue sur ![]() et
et ![]()
![]() . En passant à la limite dans l’égalité démontrée à la question 7.c, on obtient
. En passant à la limite dans l’égalité démontrée à la question 7.c, on obtient
![]()
7/ e/ On applique ici l’égalité ![]() à
à ![]() . On obtient
. On obtient
![]() d’où
d’où ![]()
Or ![]() étant le maximum de
étant le maximum de ![]() sur
sur ![]() , on a
, on a ![]() d’où
d’où
![]()
Or ![]() . On en déduit
. On en déduit
![]()
Par une récurrence du même type que celle réalisée à la question 7.c, on montre alors que pour tout ![]() ,
, ![]() . Par continuité de
. Par continuité de ![]() en passant à la limite dans cette égalité, on obtient
en passant à la limite dans cette égalité, on obtient
![]()
7/ f/ On a démontrée aux questions 7.d et 7.e que ![]() . Or
. Or ![]() et
et ![]() . On en déduit
. On en déduit
![]()
8/ a/ On note ![]() l’ensemble de définition de la fonction
l’ensemble de définition de la fonction ![]() . On a pour
. On a pour ![]() ,
,
![]()
La fonction ![]() est donc définie sur
est donc définie sur ![]() . Elle y est continue comme quotient de fonctions continues dont le dénominateur ne s’annule pas.
. Elle y est continue comme quotient de fonctions continues dont le dénominateur ne s’annule pas.
Pour tout ![]() ,
, ![]() et
et
![]()
La fonction ![]() est donc impaire.
est donc impaire.
Pour tout ![]() ,
, ![]() et
et
![]()
La fonction ![]() est donc périodique de période
est donc périodique de période ![]() .
.
8/ b/ ![]() donc
donc ![]() . Comme
. Comme ![]() , alors
, alors ![]() .
.
D’où, ![]() puis
puis
![]()
De plus, pour tout ![]() ,
, ![]() . On a
. On a ![]() . De plus, au voisinage de
. De plus, au voisinage de ![]() ,
,![]() et
et ![]() . D’où,
. D’où,
![]()
Ainsi,
![]()
8/ c/ ![]() car
car ![]() .
.
On a également, ![]() .
.
8/ d/ Soit ![]() . Si
. Si ![]() , alors
, alors ![]() avec
avec ![]() d’où
d’où ![]() et c’est absurde. De même si
et c’est absurde. De même si ![]() , alors il existe
, alors il existe ![]() tel que
tel que ![]() et
et ![]() , ce qui est absurde. Dès lors,
, ce qui est absurde. Dès lors, ![]() et
et ![]() . Et, pour tout
. Et, pour tout ![]()
![]()
Ainsi, ![]()
D’où, ![]()
à l’aide des formules de duplication.
9/ a/ Soit ![]() . Soit
. Soit ![]() . On calcule
. On calcule
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}I_N&=&\sum\limits_{n=2}^{N}\left(\frac{1}{n-\frac{x}{2}}-\frac{1}{n+\frac{x}{2}}\right)+\sum\limits_{n=2}^{N}\left(\frac{1}{n-\frac{x+1}{2}}-\frac{1}{n+\frac{x+1}{2}}\right)\\[3mm]&=&2\left(\sum\limits_{n=2}^{N}\frac{1}{2n-x}+\sum\limits_{n=2}^{N}\frac{1}{2n-1-x}-\sum\limits_{n=2}^{N}\frac{1}{2n+x}-\sum\limits_{n=2}^{N}\frac{1}{2n+1+x}\right)\\[3mm]&=&2\left(\sum\limits_{k=3}^{2N}\frac{1}{k-x}-\sum\limits_{k=4}^{2N+1}\frac{1}{k+x}\right)\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-64b89811c0995a8facfbe14d4b39aa6d_l3.png)
en regroupant les termes d’indices pair et impair dans les sommes. Alors,
![Rendered by QuickLaTeX.com \[I_N=2\left(\sum\limits_{k=3}^{2N}\frac{1}{k-x}-\sum\limits_{k=3}^{2N}\frac{1}{k+x}\right)+\frac{2}{3+x}-\frac{2}{2N+1+x}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-fee36791493b7f3c6441874c8241dd34_l3.png)
En faisant tendre ![]() vers
vers ![]() dans cette expression, il vient
dans cette expression, il vient
![]()
De plus,
![]()
Et, ![]()
Avec la formule de la question 3.b., on trouve alors
![]()
9/ b/ La fonction ![]() est continue sur
est continue sur ![]() et périodique.
et périodique.
Pour ![]() ,
, ![]() . Or, d’après la question 8.b,
. Or, d’après la question 8.b, ![]() et
et ![]() d’après la question 4.a. On en déduit que
d’après la question 4.a. On en déduit que ![]() et on prolonge
et on prolonge ![]() par continuité en
par continuité en ![]() en posant
en posant ![]()
Pour ![]() ,
, ![]() . Or, d’après la question 8.b,
. Or, d’après la question 8.b, ![]() et
et ![]() d’après la question 4.a. On en déduit que
d’après la question 4.a. On en déduit que ![]() et on prolonge
et on prolonge ![]() par continuité en
par continuité en ![]() en posant
en posant ![]() . On conclut
. On conclut
![]()
9/ c/ La fonction ![]() est donc continue sur
est donc continue sur ![]() . De plus, d’après les question 8.d et 9.a,
. De plus, d’après les question 8.d et 9.a, ![]() donc
donc ![]() . D’après la question 7.f, la fonction
. D’après la question 7.f, la fonction ![]() est alors constante sur
est alors constante sur ![]() . Comme elle vaut
. Comme elle vaut ![]() en
en ![]() , on a pour tout
, on a pour tout ![]() ,
, ![]() . La deux fonctions étant périodiques de période 1, on conclut :
. La deux fonctions étant périodiques de période 1, on conclut :
![]()
10/ a/ Pour tout ![]() ,
,
![]()
Ainsi,
![]()
10/ b/ Soit ![]() .
.
![Rendered by QuickLaTeX.com \[\delta(x)-\frac{x^2}{1-x^2}=\sum\limits_{n=2}^{\infty}\frac{1}{n^2-x^2}-\sum\limits_{n=2}^{\infty}\frac{1}{n^2}-1+\frac{1}{1-x^2}-\frac{x^2}{1-x^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-365ec062e0e5642854f2d888c285f75f_l3.png)
Or, ![]() d’où
d’où
![]()
Pour tout ![]() et pour tout
et pour tout ![]() ,
, ![]() donc
donc ![]() . On en déduit
. On en déduit
![Rendered by QuickLaTeX.com \[\fbox{\text{$\left|\delta(x)-\frac{x^2}{1-x^2}\right|=\sum\limits_{n=2}^{\infty}\frac{x^2}{n^2(n^2-x^2)}\leq x^2\sum\limits_{n=2}^{\infty}\frac{1}{n^2(n^2-1)}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f3c7947de5c72c4f528efb7e20505fbc_l3.png)
10/ c/ La fonction ![]() étant paire, il suffit de calculer la limite pour
étant paire, il suffit de calculer la limite pour ![]() . On utilise l’inégalité établie à la question 10.b.
. On utilise l’inégalité établie à la question 10.b.
![]()
Par théorème d’encadrement, on a ainsi ![]() . Or, pour
. Or, pour ![]() ,
,
![]()
Et, ![]() . D’où, par théorème d’opérations,
. D’où, par théorème d’opérations, ![]() . On en déduit
. On en déduit
![Rendered by QuickLaTeX.com \[\fbox{\text{$\lim_{x \longrightarrow 0^+} \sum\limits_{n=1}^{\infty}\frac{1}{n^2-x^2}=\lim_{x \longrightarrow 0} \sum\limits_{n=1}^{\infty}\frac{1}{n^2-x^2}=\sum\limits_{n=1}^{\infty}\frac{1}{n^2}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9c247d6f1ed22d18ac3fc7cdb6cb8390_l3.png)
10/ d/ Pour ![]() ,
,
![Rendered by QuickLaTeX.com \[\sum\limits_{n=1}^{\infty}\frac{1}{n^2-x^2}=\frac{1}{2x}\left(\frac{1}{x}-\varphi(x)\right)=\frac{1-x\varphi(x)}{2x^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-09d066be17f487aa053ae730ca791f27_l3.png)
Or, ![]() d’où
d’où ![]() . D’après la formule établie à la question 10.a, on en déduit
. D’après la formule établie à la question 10.a, on en déduit
![Rendered by QuickLaTeX.com \[\lim_{x \longrightarrow 0} \sum\limits_{n=1}^{\infty}\frac{1}{n^2-x^2}=\lim_{x \longrightarrow 0} \frac{1-x{\rm cot}(x)}{2x^2}=\frac{\pi^2}{6}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9700b99968c62c381d8af6031613b7f6_l3.png)
Par unicité de la limite
![Rendered by QuickLaTeX.com \[\fbox{\text{$\sum\limits_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f00ab66e1e504fca238aa26d3323049f_l3.png)
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie III : Développement eulérien de la fonction sinus
11/ Soit ![]() .
. ![]() . Alors
. Alors ![]() . Par comparaison avec le tg positif
. Par comparaison avec le tg positif ![]() d’une série convergente, on en déduit que la série
d’une série convergente, on en déduit que la série ![]() est absolument convergente, donc convergente.
est absolument convergente, donc convergente.
12/ a/ Soit ![]() . Par linéarité de l’intégrale,
. Par linéarité de l’intégrale,
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}{\displaystyle \int_{0}^{x}\left(\sum\limits_{n=1}^{N}\frac{-2t}{n^2-t^2}\right) dt}&=&\sum\limits_{n=1}^{N}{\displaystyle \int_0^x\frac{-2t}{n^2-t^2}dt}\\&=&\sum\limits_{n=1}^{N}\left[\ln(n^2-t^2)\right]_0^x\\&=&\sum\limits_{n=1}^{N}\ln\left(1-\frac{x^2}{n^2}\right)\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ef603527daa350d0aeb827d4c63d819d_l3.png)
Donc,
![Rendered by QuickLaTeX.com \[\fbox{\text{${\displaystyle \int_{0}^{x}\left(\sum\limits_{n=1}^{N}\frac{-2t}{n^2-t^2}\right) dt}=\beta_N(x)$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d7e9b464405d55cbef9eb0c3f47f81e4_l3.png)
12/ b/ La fonction ![]() est continue sur
est continue sur ![]() d’après la partie I, d’après le théorème d’opérations. De plus, d’après la question I.4.a, la fonction
d’après la partie I, d’après le théorème d’opérations. De plus, d’après la question I.4.a, la fonction ![]() est prolongeable par continuité en
est prolongeable par continuité en ![]() . On en déduit que pour
. On en déduit que pour ![]() , l’intégrale
, l’intégrale ![]() converge.
converge.
12/ c/ Soit ![]() .
.

Or, pour tout ![]() ,
, ![]() donc pour tout
donc pour tout ![]() ,
, ![]() d’où
d’où ![]() . D’où,
. D’où,
![Rendered by QuickLaTeX.com \[\left|{\displaystyle \int_0^x\left(\varphi(t)-\frac{1}{t}\right)dt}-{\ds \int_0^x\left(\sum\limits_{n=1}^{N}\frac{-2t}{n^2-t^2}\right)dt}\right| \leq \sum\limits_{n=N+1}{\infty}\frac{{\ds \int_{0}^{x}2t \, dt}}{n^2-1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d80a9aaad7e90fd79311610829984b7a_l3.png)
Or, ![]() . On en déduit
. On en déduit
![Rendered by QuickLaTeX.com \[\fbox{\text{$\left|{\displaystyle \int_0^x\left(\varphi(t)-\frac{1}{t}\right)dt}-{\ds \int_0^x\left(\sum\limits_{n=1}^{N}\frac{-2t}{n^2-t^2}\right)dt}\right| \leq \sum\limits_{n=N+1}^{\infty}\frac{1}{n^2-1}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5c7a0950e0345987327b6c67e5e07153_l3.png)
12/ d/ Soit ![]() . D’après les questions précédentes, on en déduit pour tout
. D’après les questions précédentes, on en déduit pour tout ![]() ,
,
![Rendered by QuickLaTeX.com \[\left|{\ds \int_0^x\left(\varphi(t)-\frac{1}{t}\right)dt}-\beta_N(x)\right|\leq \sum\limits_{n=N+1}^{\infty}\frac{1}{n^2-1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-adb7f5543c846db5d72b36d23ad23157_l3.png)
La série de terme général ![]() étant convergente,
étant convergente, ![]() . De plus,
. De plus, ![]() . On en déduit d’après le théorème d’encadrement et l’unicité de la limite
. On en déduit d’après le théorème d’encadrement et l’unicité de la limite
![]()
12/ e/ Soit ![]() . D’après la question II.9, on a pour tout
. D’après la question II.9, on a pour tout ![]() ,
,
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}{\ds \int_{y}^x\left(\varphi(t)-\frac{1}{t}\right) dt}&=&{\ds \int_{y}^{x}\pi \frac{\cos(\pi t)}{\sin(\pi t)} dt}-{\ds \int_y^x\frac{1}{t} dt}\\[3mm]&=&\left[\ln(\sin(\pi t))\right]_y^x-[\ln (\pi t)]_y^x\\[3mm]&=&\ln\left(\frac{\sin(\pi x)}{\pi x}\right)-\ln\left(\frac{\sin(\pi y)}{\pi y}\right)\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a30a764fa9a10fe83f80249b2043094b_l3.png)
Or, ![]() d’où
d’où ![]() . En passant à la limite dans l’expression précédente, on en déduit :
. En passant à la limite dans l’expression précédente, on en déduit :
![]()
13/ a/ Soit ![]() . Pour tout
. Pour tout ![]() et pour tout
et pour tout ![]() ,
, ![]() donc
donc ![]() , d’où
, d’où ![]() . La suite
. La suite ![]() convergeant, on en déduit par somme que la suite
convergeant, on en déduit par somme que la suite ![]() converge. On en déduit que la suite
converge. On en déduit que la suite ![]() est convergente.
est convergente.
13/ b/ Soit ![]() . La fonction
. La fonction ![]() étant continue sur
étant continue sur ![]() , en passant à la limite dans l’égalité précédente, il vient
, en passant à la limite dans l’égalité précédente, il vient
![]()
D’où,
![]()
13/ c/ Soit ![]() . Il existe
. Il existe ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]() d’où
d’où ![]() . De la même manière qu’à la question 11/, on montre que la série
. De la même manière qu’à la question 11/, on montre que la série ![]() converge. Dès lors la suite
converge. Dès lors la suite ![]() converge. En la multipliant par un nombre fini de termes, il vient que la suite
converge. En la multipliant par un nombre fini de termes, il vient que la suite ![]() converge.
converge.
13/ d/ Soit ![]() et
et ![]() .
.
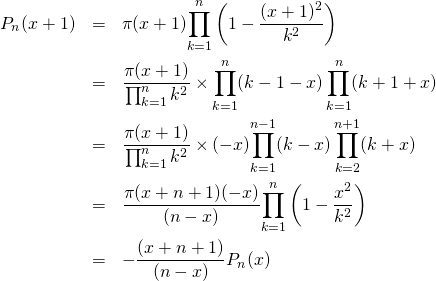
13/ e/ Soit ![]() . D’après la question précédente, pour tout
. D’après la question précédente, pour tout ![]() ,
,
![]()
![]() . En passant à la limite dans l’expression précédente, on obtient
. En passant à la limite dans l’expression précédente, on obtient
![]()
Pour tout ![]() ,
,
![]()
La fonction ![]() est alors
est alors ![]() -périodique sur
-périodique sur ![]() .
.
13/ f/ Soit ![]() , alors
, alors ![]() . Donc
. Donc ![]() d’après la question 13.b. De plus, d’après la question 13.f,
d’après la question 13.b. De plus, d’après la question 13.f, ![]() . On a donc montré que pour tout
. On a donc montré que pour tout ![]() ,
, ![]() . La fonction
. La fonction ![]() est
est ![]() -périodique sur
-périodique sur ![]() tout comme la fonction
tout comme la fonction ![]() . On en déduit alors
. On en déduit alors
![]()
Partie IV : Un autre développement du sinus
14/ Soit ![]() . Pour tout
. Pour tout ![]() ,
, ![]() donc
donc ![]() existe. De plus,
existe. De plus, ![]() . Par comparaison avec le multiple d’une série de Riemann convergente, la série de tg
. Par comparaison avec le multiple d’une série de Riemann convergente, la série de tg ![]() est absolument convergente, donc convergente.
est absolument convergente, donc convergente.
15/ Soit ![]() . Soit
. Soit ![]() .
.
Les fonctions ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() . Par intégration par parties, il vient
. Par intégration par parties, il vient
![]()
Les fonctions ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() . Par intégration par parties, il vient
. Par intégration par parties, il vient
![]()
Dès lors,
![]()
En utilisant la formule indiquée dans l’énoncé, on pouvait procéder autrement.
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}\lambda_n(x)&=&\frac{1}{2}{\ds \int_0^{\pi}\cos((x+n)t) dt}+\frac{1}{2}{\ds \int_0^{\pi}\cos((x-n)t) dt}\\[3mm]&=&\frac{1}{2}\left[\frac{\sin((x+n)t)}{x+n}\right]_0^{\pi}+\frac{1}{2}\left[\frac{\sin((x-n)t)}{x-n}\right]_0^{\pi}\\[3mm]&=&(-1)^n\frac{\sin(x\pi)}{2(x+n)}+(-1)^n\frac{\sin(x\pi)}{2(x-n)}\\[3mm]&=&(-1)^n\frac{\sin(\pi x)}{2(x^2-n^2)}(x-n+x+n)\\[3mm]&=&\frac{(-1)^{n-1}x\sin(\pi x)}{n^2-x^2}\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-fd6dea84c83163eb27bdee15116528a2_l3.png)
16/ Soit ![]() et
et ![]() .
.
a/ ![]() . Pour
. Pour ![]() avec
avec ![]() ,
, ![]() et
et ![]() , d’où
, d’où
![Rendered by QuickLaTeX.com \begin{eqnarray*}C_n(t)&=&\frac{1}{2}e^{it}\frac{e^{nit}-1}{e^{it}-1}+\frac{1}{2}e^{-it}\frac{e^{-nit}-1}{e^{-it}-1}\\[4mm]&=&\frac{1}{2}e^{i(n+1)t/2}\frac{\sin(nt/2)}{\sin(t/2)}+\frac{1}{2}e^{-i(n+1)t/2}\frac{\sin(nt/2)}{\sin(t/2)}\\ &=&\cos((n+1)t/2)\frac{\sin(nt/2)}{\sin(t/2)}\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-bce4313cbd4b33601be47a233a89f59d_l3.png)
De plus,
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}\sin((2n+1)t/2)-\sin(t/2)&=&\sin((n+1)t/2)\cos(nt/2)+\cos((n+1)t/2)\sin(nt/2)\\&-&\sin((n+1)t/2)\cos(nt/2)+\sin(nt/2)\cos((n+1)t/2)\\&=&2\cos((n+1)t/2)\sin(nt/2)\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-368e70fdd5e7157ed92bb0034e545561_l3.png)
On en déduit que
![]()
16/ b/ Si ![]() avec
avec ![]() , pour tout
, pour tout ![]() ,
, ![]() donc
donc ![]() .
.
16/ c/ Par linéarité de l’intégrale,
![]()
17/ Les fonctions ![]() et
et ![]() étant de classe
étant de classe ![]() sur
sur ![]() , en intégrant par parties, on obtient
, en intégrant par parties, on obtient
![]()
La fonction ![]() étant de classe
étant de classe ![]() , elle est bornée sur
, elle est bornée sur ![]() par un réel
par un réel ![]() de même que sa dérivée
de même que sa dérivée ![]() par
par ![]() et que la fonction
et que la fonction ![]() qui est bornée par
qui est bornée par ![]() . On a donc
. On a donc
![]()
Or,
![]()
18/ a/ La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() comme quotient de deux fonctions de classe
comme quotient de deux fonctions de classe ![]() dont le dénominateur ne s’annule pas.
dont le dénominateur ne s’annule pas.
Au voisinage de ![]() , comme
, comme ![]() et
et ![]() , on a
, on a
![]()
On en déduit au voisinage de ![]()
![]() . Or,
. Or, ![]() , on en déduit que
, on en déduit que ![]() est continue en
est continue en ![]() et dérivable en
et dérivable en ![]() avec
avec ![]() .
.
Or, pour tout ![]() ,
,
![]()
On détermine un équivalent de cette expression en considérant des développements limités d’ordre 2 du numérateur et du dénominateur. On obtient au voisinage de ![]() ,
,
![]()
D’où, ![]() . La fonction
. La fonction ![]() est donc continue en
est donc continue en ![]() et on en déduit que
et on en déduit que
![]()
18/ b/ Soit ![]() . D’après la question 16.a, on a directement
. D’après la question 16.a, on a directement
![]()
De plus, d’après la question 16.b, ![]() donc
donc ![]() . De plus,
. De plus,
![]()
On a donc le résultat voulu aussi pour ![]() .
.
18/ c/ Soit ![]() et soit
et soit ![]() . Par linéarité de l’intégrale,
. Par linéarité de l’intégrale,
![]()
En utilisant la quantité ![]() , on a encore avec la question 18.b
, on a encore avec la question 18.b
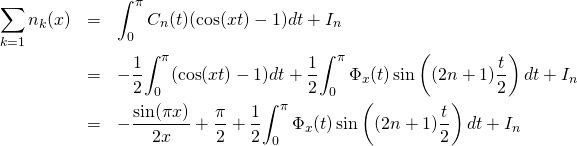
19/ a/ Soit ![]() . Partons de l’expression établie à la question 18.c. Pour tout
. Partons de l’expression établie à la question 18.c. Pour tout ![]() ,
, ![]() . De plus, la fonction
. De plus, la fonction ![]() étant de classe
étant de classe ![]() sur
sur ![]() , on en déduit d’après la question 17 que
, on en déduit d’après la question 17 que
![]()
De plus, d’après la question 15, pour tout ![]() ,
,
![Rendered by QuickLaTeX.com \[\sum\limits_{k=1}^{n}\lm_k(x)=\sin(\pi x)\sum\limits_{k=1}{n}\nu_k(x)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5eeddb5ce61405b257e77fb61622c8f0_l3.png)
Or, ![]() . Dès lors en passant à la limite dans l’expression établie à la question 18.c, on obtient
. Dès lors en passant à la limite dans l’expression établie à la question 18.c, on obtient
![]()
19/ b/ Soit ![]() . On a donc
. On a donc ![]() . En divisant l’expression de la question précédente par
. En divisant l’expression de la question précédente par ![]() , on obtient
, on obtient
![]()
D’où,
![Rendered by QuickLaTeX.com \[\fbox{\text{$\frac{\pi}{\sin(\pi x)}=\frac{1}{x}+2x\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2-x^2}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4157c52533cc91cfa2922ee2bc4f7a0e_l3.png)

