Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet ESSEC Maths ECS 2017
Revenir à tous les corrigés des annales de maths BCE
Partie 0 : Étude d’un premier exemple dans 
1/ On prend ici ![]() et
et ![]() . Soit
. Soit ![]() comme
comme ![]() , on a
, on a ![]()
Ainsi ![]() car
car ![]() Et
Et ![]()
Donc ![]() et
et ![]() avec
avec ![]() Finalement
Finalement ![]() n’est pas un point extremal de
n’est pas un point extremal de ![]()
On donne un exemple ci-dessous avec ![]() donc
donc ![]()
![]()
2/ On considère maintenant ![]() et
et ![]() . La question précédente montre avec de mineures adaptations qu’aucun point de
. La question précédente montre avec de mineures adaptations qu’aucun point de ![]() n’est extremal de
n’est extremal de ![]() .
.
Montrons que 0 est extremal de ![]() Supposons qu’il existe
Supposons qu’il existe ![]() dans
dans ![]() tel que
tel que ![]() Or une somme de réels positifs est nulle si et seulement si tous les termes sont nuls donc ici
Or une somme de réels positifs est nulle si et seulement si tous les termes sont nuls donc ici ![]() Ainsi 0 est extrémal de
Ainsi 0 est extrémal de ![]()
Montrons que 1 est extremal de ![]() Supposons qu’il existe
Supposons qu’il existe ![]() dans
dans ![]() tel que
tel que ![]() Si
Si ![]() alors
alors ![]() car
car ![]() . C’est absurde donc
. C’est absurde donc ![]() et
et ![]() Ainsi 1 est extrémal de
Ainsi 1 est extrémal de ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie 1 : Étude d’un second exemple dans  .
.
3/ a/ ![]()
![]()
![]()
On voit alors que ![]() est un paramétrage du segment d’extrémités
est un paramétrage du segment d’extrémités ![]() et
et ![]() dans
dans ![]()
3/ b/ Soient ![]() et
et ![]() . Par calcul simple, on voit que
. Par calcul simple, on voit que
![]()
Comme ![]() on a
on a ![]() , ainsi
, ainsi ![]() .
.
3/ c/ Soit ![]() est inversible si et seulement si
est inversible si et seulement si ![]() si et seulement si
si et seulement si ![]() si et seulement si
si et seulement si ![]() Si c’est le cas alors
Si c’est le cas alors
![]()
Voyons pour quelles valeurs de ![]() , on a
, on a ![]()
Si ![]() alors
alors ![]() donc
donc ![]() , on divise par
, on divise par ![]() et
et ![]() Donc
Donc ![]()
Si ![]() alors
alors ![]() donc
donc ![]() et
et ![]()
Si ![]() alors
alors ![]() inversible d’inverse
inversible d’inverse ![]()
Si ![]() alors
alors ![]() inversible d’inverse
inversible d’inverse ![]()
Bilan : ![]() est inversible avec
est inversible avec ![]() si et seulement si
si et seulement si ![]() ou
ou ![]() .
.
4/ Points extrémaux de ![]() .
.
a/ On peut remarquer que, pour tout ![]() on a
on a
![]()
Par conséquent, pour tout ![]() on a, en exploitant la question 2,
on a, en exploitant la question 2,
![]()
De même on peut remarquer que, pour tout ![]() on a
on a
![]()
Par conséquent, pour tout
![]()
Bilan : ![]() et
et ![]() sont des points extrémaux de
sont des points extrémaux de ![]() .
.
4/ b/ Soit ![]() . On a
. On a ![]() Avec la question (3b),
Avec la question (3b), ![]() .
.
Comme ![]() on a
on a ![]() donc
donc ![]() n’est pas extrémal.
n’est pas extrémal.
4/ c/ Soit ![]() , alors
, alors ![]() et
et ![]() .
.
On a ![]() donc
donc ![]()
Bilan : ![]() n’est pas extrémal.
n’est pas extrémal.
5/ Réduction simultanée des matrices de ![]() .
.
a/ Soit ![]() la matrice
la matrice ![]() est non inversible si et seulement si
est non inversible si et seulement si ![]() si et seulement si
si et seulement si ![]()
Les valeurs propres de ![]() sont
sont ![]() et
et ![]() On voit facilement que
On voit facilement que ![]() et
et ![]() . Il y a deux valeurs propres dans
. Il y a deux valeurs propres dans ![]() , un espace de dimension 2, donc
, un espace de dimension 2, donc ![]() est diagonalisable et les deux SEP sont des droites.
est diagonalisable et les deux SEP sont des droites.
Bilan : SEP(![]() et SEP(
et SEP(![]() .
.
b/ Il est clair que ![]() et
et ![]() donc
donc ![]() et
et ![]() sont vecteurs propres de
sont vecteurs propres de ![]() associés à 1.
associés à 1.
Ainsi, pour tout ![]() de
de ![]() ,
, ![]()
![]()
Donc ![]() possède deux vecteurs propres formant une famille sur un espace de dimension 2 donc
possède deux vecteurs propres formant une famille sur un espace de dimension 2 donc ![]() est diagonalisable avec la base de vecteurs propres suivante :
est diagonalisable avec la base de vecteurs propres suivante : ![]() . Les valeurs propres associées sont
. Les valeurs propres associées sont ![]() et
et ![]() . Il y a égalité entre
. Il y a égalité entre ![]() et 1 si et seulement si
et 1 si et seulement si ![]()
Dans tous les cas, selon le cours, ![]() est telle que, pour tout
est telle que, pour tout ![]() de
de ![]() ,
, ![]() avec
avec ![]()
c/ Soit ![]() dans
dans ![]() . On note
. On note ![]() l’endomorphisme de
l’endomorphisme de ![]() représenté par la matrice
représenté par la matrice ![]() dans la base canonique de
dans la base canonique de ![]() .
.
On sait que ![]() est un projecteur de
est un projecteur de ![]() si et seulement si
si et seulement si ![]() si et seulement si
si et seulement si ![]()
On voit que ![]() donc
donc
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Comme ![]() est libre on a
est libre on a ![]()
Pour ![]() on a
on a ![]() de noyau
de noyau ![]() et d’image
et d’image ![]()
Pour ![]() on a
on a ![]() de noyau Vect(
de noyau Vect(![]() et d’image Vect(
et d’image Vect(![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie 2 : Points extrémaux et diamètre d’une partie bornée d’un espace euclidien.
6/ ![]() est non vide donc on peut choisir un
est non vide donc on peut choisir un ![]() dans
dans ![]() et le nombre
et le nombre ![]() est dans l’ensemble
est dans l’ensemble ![]() donc il est une partie non vide de
donc il est une partie non vide de ![]() .
.
Pour tout ![]() dans
dans ![]() ,
, ![]() par inégalité triangulaire donc l’ensemble
par inégalité triangulaire donc l’ensemble ![]() est majoré par
est majoré par ![]()
7/ On considère donc ![]() tels que
tels que ![]() .
.
a/ ![]() par inégalité triangulaire.
par inégalité triangulaire.
Par définition du diamètre, on peut dire que ![]() et
et ![]() . On somme ces inégalités et on divise par 2 pour obtenir
. On somme ces inégalités et on divise par 2 pour obtenir ![]()
De sorte que, par double inégalité, ![]()
Si ![]() alors
alors ![]() ne contient qu’un seul élément et il est extrémal dans
ne contient qu’un seul élément et il est extrémal dans ![]()
Si ![]() alors on peut diviser par
alors on peut diviser par ![]() ainsi
ainsi
![]()
Par définition ![]() et
et ![]() , on sait que 1 est extrémal dans
, on sait que 1 est extrémal dans ![]() donc
donc ![]()
Bilan : ![]() .
.
b/ ![]()
![]()
![]()
![]()
Comme ![]() on peut les retirer simultanément et
on peut les retirer simultanément et ![]() donc
donc ![]()
c/ Les variables ![]() et
et ![]() jouent des rôles symétriques donc
jouent des rôles symétriques donc ![]() .
.
d/ Comme ![]() , on a
, on a ![]() donc
donc ![]() et
et
![]()
donc ![]()
donc ![]() et
et ![]()
Bilan : ![]() et
et ![]() sont orthogonaux.
sont orthogonaux.
e/ ![]() et
et ![]() sont orthogonaux donc
sont orthogonaux donc ![]() et
et ![]() sont orthogonaux. On peut appliquer le théorème de Pythagore et
sont orthogonaux. On peut appliquer le théorème de Pythagore et
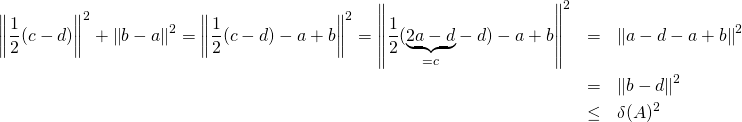
car ![]() et
et ![]() sont dans
sont dans ![]()
D’autre part ![]() donc
donc ![]() donc
donc ![]() et
et ![]() . On en déduit
. On en déduit ![]()
Bilan : ![]() est extrémal dans
est extrémal dans ![]()
Remarque : de façon intuitive, s’il existe ![]() orthogonal à
orthogonal à ![]() , alors on pourra trouver un vecteur
, alors on pourra trouver un vecteur ![]() dans
dans ![]() tel que
tel que ![]() ce qui est contradictoire avec la notion de diamètre. En ce sens
ce qui est contradictoire avec la notion de diamètre. En ce sens ![]() est un point sur le « bord » de
est un point sur le « bord » de ![]() ce qui permet à
ce qui permet à ![]() d’être maximal.
d’être maximal.
![Rendered by QuickLaTeX.com \[\begin{picture}(10, 10) \end{picture} \put(-5, 0){\oval(60, 10)}\put(-35,0){\line(1,0){60}}\put(-45,-2){$a$}\put(27,0){$b$}\put(-45,15){$c$}\put(-45,-18){$d$}\put(-35,-15){\line(0,1){30}} \end{picture}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ad08e428c147fd3aa416d876b6e7088d_l3.png)
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie 3 : Étude de l’ensemble des matrices bistochastiques et de ses points extrémaux.
8/ Premières propriétés de ![]() .
.
a/ Soit ![]() dans
dans ![]() . Soit
. Soit ![]() et, pour tout
et, pour tout ![]()
De plus ![]() et
et ![]() .
.
Bilan : ![]() et
et ![]() .
.
On note 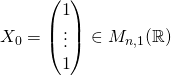 , le vecteur colonne dont toutes les composantes valent 1.
, le vecteur colonne dont toutes les composantes valent 1.
b/ Soit ![]() . Soit
. Soit ![]() le produit
le produit ![]() est un vecteur colonne dont le
est un vecteur colonne dont le ![]() terme est
terme est ![]() car on multiplie la
car on multiplie la ![]() ligne de
ligne de ![]() par une colonne de 1. Donc
par une colonne de 1. Donc ![]() vaut 1.
vaut 1.
Bilan : ![]() .
.
c/ Réciproquement, soit ![]() une matrice de
une matrice de ![]() dont tous les coefficients sont positifs, et vérifiant :
dont tous les coefficients sont positifs, et vérifiant : ![]() et
et ![]() . Alors pour tout
. Alors pour tout ![]() on a
on a ![]() et
et
![]()
Bilan : ![]() .
.
d/ Soit ![]() dans
dans ![]() . Soit
. Soit ![]()
donc ![]()
![Rendered by QuickLaTeX.com \[\underset{\text{\tiny{inversion des $\sum$ possible car les indices sont ind\'ependants avec un nombre fini de termes}}}{\underbrace{\sum\limits_{k=1}^n (M)_{i,k} \sum\limits_{j=1}^n(M')_{k,j}}}=\sum\limits_{k=1}^n (M)_{i,k}\underset{=1}{\underbrace{s_L(M',k)}}=\sum\limits_{k=1}^n (M)_{i,k}=1.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b32432653c31ebf67725728667760fa5_l3.png)
De même ![]()
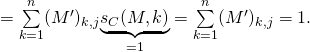
Bilan : ![]() .
.
9/ a/ Si ![]() est l’identité de
est l’identité de ![]() , alors
, alors ![]() donc
donc ![]() car
car ![]() et
et ![]() co\ »\i ncident sur une base de
co\ »\i ncident sur une base de ![]() et
et ![]() .
.
b/ Si ![]() est une permutation de
est une permutation de ![]() , alors, pour tout
, alors, pour tout ![]() donc dans la
donc dans la ![]() colonne de
colonne de ![]() il y
il y ![]() termes nuls et un terme égal à 1 qui est sur la ligne
termes nuls et un terme égal à 1 qui est sur la ligne ![]() . Donc
. Donc ![]()
Soit ![]() comme
comme ![]() est une permutation de
est une permutation de ![]() il existe un seul
il existe un seul ![]() tel que
tel que ![]() donc la ligne
donc la ligne ![]() de
de ![]() contient
contient ![]() termes nuls et un terme égal à 1 qui est sur la colonne
termes nuls et un terme égal à 1 qui est sur la colonne ![]() Donc
Donc ![]()
On remarque aussi que tous les coefficients de ![]() sont positifs car ils valent 1 ou 0.
sont positifs car ils valent 1 ou 0.
Bilan : ![]() .
.
Ce qui précède permet de dire que, pour tout ![]()
![]() si et seulement si
si et seulement si ![]() si et seulement si
si et seulement si ![]()
Donc ![]() si et seulement si
si et seulement si ![]() si et seulement si
si et seulement si ![]() si et seulement si
si et seulement si ![]()
Or ![]() si et seulement si
si et seulement si ![]() si et seulement si
si et seulement si ![]()
On voit que ![]() et
et ![]() ont des 1 sur les mêmes positions et des 0 sur les mêmes positions donc elles sont égales.
ont des 1 sur les mêmes positions et des 0 sur les mêmes positions donc elles sont égales.
Bilan : ![]() .
.
c/ Soit ![]() , soit
, soit ![]()
![]()
Donc ![]() et
et ![]() coïncident sur une base de
coïncident sur une base de ![]() donc sont égaux.
donc sont égaux.
Par conséquent ![]() de même
de même ![]()
Par traduction matricielle dans la base canonique on a ![]() inversible et
inversible et ![]()
d/ On vient de montrer que, pour tout ![]() ,
, ![]() est inversible et
est inversible et ![]() Donc
Donc ![]() est orthogonale.
est orthogonale.
e/ On a vu que les matrices ![]() présentant sur chaque ligne et sur chaque colonne un 1 et
présentant sur chaque ligne et sur chaque colonne un 1 et ![]() fois 0.
fois 0.
Réciproquement soit ![]() une matrice d’ordre
une matrice d’ordre ![]() présentant sur chaque ligne et sur chaque colonne un 1 et
présentant sur chaque ligne et sur chaque colonne un 1 et ![]() fois 0.
fois 0.
Soit ![]() on note
on note ![]() la ligne où se trouve l’unique 1 dans la colonne
la ligne où se trouve l’unique 1 dans la colonne ![]() de
de ![]() On a bien s\^ur
On a bien s\^ur ![]() . On peut définir alors la fonction
. On peut définir alors la fonction ![]() telle que, pour tout
telle que, pour tout ![]() .
.
Si ![]() il y a un 1 sur la ligne
il y a un 1 sur la ligne ![]() et sur les colonnes
et sur les colonnes ![]() et
et ![]() , par définition de
, par définition de ![]() cela implique
cela implique ![]() donc
donc ![]() est injective.
est injective.
Comme il y a un 1 sur chaque ligne de ![]() on peut dire que
on peut dire que ![]() est surjective.
est surjective.
Donc ![]() est une permutation de
est une permutation de ![]() et
et ![]()
Bilan : les matrices ![]() sont exactement les matrices présentant sur chaque ligne et sur chaque colonne un 1 et
sont exactement les matrices présentant sur chaque ligne et sur chaque colonne un 1 et ![]() fois 0.
fois 0.
10/ Soit ![]() . montrons que, pour tout
. montrons que, pour tout ![]() on a
on a ![]()
Par hypothèse les coefficients de ![]() sont positifs donc
sont positifs donc ![]() en effet la somme
en effet la somme ![]() contient le terme
contient le terme ![]() est les autres sont positifs.
est les autres sont positifs.
Soit ![]() dans
dans ![]() telles que
telles que ![]() alors pour tout
alors pour tout ![]() donc
donc ![]() . On sait que
. On sait que ![]() vaut 0 ou 1 et que les deux sont extrémaux dans
vaut 0 ou 1 et que les deux sont extrémaux dans ![]() donc
donc ![]()
Par conséquent ![]()
Bilan : ![]() est un point extrémal de
est un point extrémal de ![]() .
.
11/ Etude d’un projecteur : on note ![]() et
et ![]() .
.
a/ Soit ![]() fixé dans
fixé dans ![]() . L’application
. L’application ![]() est une bijection de
est une bijection de ![]() dans lui même car l’application
dans lui même car l’application ![]() est bijective donc l’application
est bijective donc l’application ![]() existe et elle vérifie
existe et elle vérifie
![]()
On utilise la linéarité de ![]() pour écrire
pour écrire
![Rendered by QuickLaTeX.com \[f_{\tau} \circ p = f_{\tau} \circ\left(\frac{1}{n!}\; \sum_{\sigma \in S_n} f_{\sigma}\right)=\frac{1}{n!}\; \sum_{\sigma \in S_n} f_{\tau} \circ f_{\sigma}=\frac{1}{n!}\; \sum_{\sigma \in S_n} f_{\tau \circ\sigma}=\frac{1}{n!}\; \sum_{\sigma \in S_n} f_{\varphi_{\tau}(\sigma)}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cde96d27d0cea244e8b9fafb5ff2e79f_l3.png)
or ![]() est une bijection de
est une bijection de ![]() dans lui même donc
dans lui même donc ![]() d’où
d’où ![]() .
.
Bilan : ![]()
b/ Pour montrer que ![]() on calcule
on calcule
![Rendered by QuickLaTeX.com \[p\circ p = \left(\frac{1}{n!}\; \sum_{\sigma \in S_n} f_{\sigma}\right)\circ p=\frac{1}{n!}\; \sum_{\sigma \in S_n} f_{\sigma}\circ p=\frac{1}{n!}\; \sum_{\sigma \in S_n} p = \frac{1}{n!}\times n! \times p = p\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2cf3b1c88726b39a77720197847fc033_l3.png)
car il y a
Bilan : ![]() est un projecteur de
est un projecteur de ![]() .
.
c/ Comme ![]() est un projecteur, on sait que, pour tout
est un projecteur, on sait que, pour tout ![]() , on a
, on a ![]()
Ainsi soit ![]() alors, pour tout
alors, pour tout ![]() on a
on a ![]()
Réciproquement si, pour tout ![]() on a
on a ![]() alors
alors ![]()
Bilan : ![]() .
.
d/ Soit ![]() , il est facile de voir que, pour tout
, il est facile de voir que, pour tout ![]()
![Rendered by QuickLaTeX.com \[\ f_{\sigma}(x)=f_{\sigma}\left(\sum\limits_{i=1}^n e_i\right)= \sum\limits_{i=1}^n f_{\sigma}(e_i)=\sum\limits_{i=1}^n e_{\sigma(i)}=\sum\limits_{i=1}^n e_{i}=x\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b40ec067db8c37bf5b4680ddced27b89_l3.png)
Réciproquement soit ![]() tel que, pour tout
tel que, pour tout ![]() Soit
Soit ![]() et
et ![]() distincts dans
distincts dans ![]() On considère la permutation
On considère la permutation ![]() qui échange
qui échange ![]() et
et ![]() et laisse fixes les autres valeurs.
et laisse fixes les autres valeurs.
C’est-à-dire ![]() et, pour
et, pour ![]()
On a :
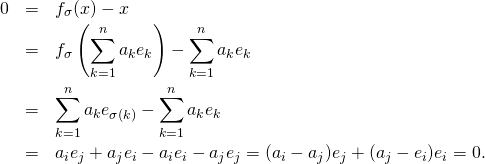
Donc comme ![]() est sous-famille d’une base elle est libre et
est sous-famille d’une base elle est libre et ![]() et cela pour tout
et cela pour tout ![]() donc
donc ![]()
On en déduit que ![]()
Bilan : ![]()
e/ On a :
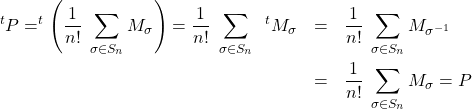
car ![]()
On en déduit que la matrice de ![]() dans une base orthonormée, est symetrique donc
dans une base orthonormée, est symetrique donc ![]() est un projecteur orthogonal.
est un projecteur orthogonal.
On sait que les matrices ![]() ne contiennent que des 0 et des 1. On pose
ne contiennent que des 0 et des 1. On pose ![]() Soit
Soit ![]()
![]() est le nombre de permutations de
est le nombre de permutations de ![]() qui, à
qui, à ![]() associent
associent ![]() Il y en a
Il y en a ![]() c’est-à-dire le nombre de façons de permuter les entiers de
c’est-à-dire le nombre de façons de permuter les entiers de ![]() distincts de
distincts de ![]() On en déduit que tous les ceofficients de
On en déduit que tous les ceofficients de ![]() valent
valent ![]() . Donc en divisant par
. Donc en divisant par ![]() , on voit que
, on voit que ![]() a tous ses coefficients égaux à
a tous ses coefficients égaux à ![]()
f/ Les colonnes et lignes de ![]() contiennent chacune
contiennent chacune ![]() fois le terme
fois le terme ![]() qui est positif donc les sommes des termes valent 1 sur chaque ligne et colonne.
qui est positif donc les sommes des termes valent 1 sur chaque ligne et colonne.
Bilan : ![]() .
.
12/ a/ Si ![]() et
et ![]() sont deux matrices de
sont deux matrices de ![]() ,
,
![Rendered by QuickLaTeX.com \[\text{Tr}(^tM.N)=\sum_{i=1}^n(^tM.N)_{i,i}=\sum_{i=1}^n\sum_{j=1}^n(^tM)_{i,j}(N)_{j,i}=\sum_{i=1}^n\sum_{j=1}^n(M)_{j,i}(N)_{j,i}=\sum_{i=1}^n\sum_{j=1}^nm_{j,i}n_{j,i}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-360b6c4040888fbdcdef6380d912d404_l3.png)
b/ L’application ![]() est un produit scalaire sur
est un produit scalaire sur ![]() , c’est un résultat classique du cours.
, c’est un résultat classique du cours.
Si ![]() sont dans
sont dans ![]() , on note
, on note ![]() ce produit scalaire, et
ce produit scalaire, et ![]() la norme associée.
la norme associée.
c/ Soit ![]() . On a
. On a 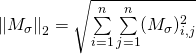 . Or dans la matrice
. Or dans la matrice ![]() il y a
il y a ![]() coefficients valant 1, les autres sont nuls donc
coefficients valant 1, les autres sont nuls donc ![]()
d/ Dans cette question seulement, on suppose que ![]() . Soit
. Soit ![]() et
et ![]() . Par définition
. Par définition
![]()
Or ![]() et
et ![]() donc
donc ![]() donc
donc ![]() et pour
et pour ![]() on a
on a ![]()
Bilan : ![]() .
.
e/ Soit ![]() . Soit
. Soit ![]() . On sait que les coefficients de
. On sait que les coefficients de ![]() sont positifs et que la somme des termes de chaque ligne vaut 1 donc tous les coefficients sont dans
sont positifs et que la somme des termes de chaque ligne vaut 1 donc tous les coefficients sont dans ![]() donc, pour tout
donc, pour tout ![]() on a
on a ![]() donc
donc ![]() On en déduit que
On en déduit que
![Rendered by QuickLaTeX.com \[\left\|M\right\|_2^2 =\sum\limits_{i=1}^n\sum\limits_{j=1}^n m_{i,j}^2\leq \sum\limits_{i=1}^n 1=n.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-35a72aee7a882ae0a7d9e4080ecd121a_l3.png)
Bilan : ![]() .
.
f/ On en déduit que
![Rendered by QuickLaTeX.com \[\forall (M,N) \in A_n^2\ , \ \left\|M-N\right\|_2^2 =\left\|M\right\|_2^2+\left\|N\right\|_2^2-2\langle M,N\rangle \leq 2n -2\langle M,N\rangle =2n-\sum_{i=1}^n\sum\limits_{j=1}^nm_{j,i}n_{j,i}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a066686c7825e82a610c3bf3bcadef15_l3.png)
Or ![]() car les coefficients de
car les coefficients de ![]() et
et ![]() sont positifs.
sont positifs.
Donc ![]() . On compose par la fonction racine carrée qui est croissante sur
. On compose par la fonction racine carrée qui est croissante sur ![]() et
et ![]() sachant qu’une norme est positive.
sachant qu’une norme est positive.
g/ Soit ![]() , on définit
, on définit ![]() de la façon suivante. Pour tout
de la façon suivante. Pour tout ![]() si
si ![]() on pose
on pose ![]() , et si
, et si ![]() on pose
on pose ![]() Il est clair que
Il est clair que ![]() a
a ![]() images distinctes et que
images distinctes et que ![]() est injectif donc
est injectif donc ![]() est dans
est dans ![]() On remarque que, pour tout
On remarque que, pour tout ![]()
![]()
On en déduit que ![]() . En effet,
. En effet,
pour tout ![]()
![]() si et seulement si
si et seulement si ![]() car
car ![]() valent 1 ou 0.
valent 1 ou 0.
Or ![]() si et seulement si
si et seulement si ![]() et
et ![]() ce qui est impossible.
ce qui est impossible.
Bilan : ![]()
h/ La question 12(f) assure que diamètre de ![]() est dominé par
est dominé par ![]() Or il existe
Or il existe ![]() et
et ![]() dans
dans ![]() tel que
tel que ![]() On sait que
On sait que ![]() sont dans
sont dans ![]() de sorte que
de sorte que
![]()
Donc ![]() cela implique que le majorant
cela implique que le majorant ![]() est un maximum et que le diamètre de
est un maximum et que le diamètre de ![]() est
est ![]()
La partie II assure alors que ![]() est un point extrémal de
est un point extrémal de ![]() On peut faire ce raisonnement pour tout
On peut faire ce raisonnement pour tout ![]()
Bilan : les matrices de permutation sont des points extrémaux de ![]() .
.
13/ a/
![]()
![]() ;
;![]() la matrice nulle de
la matrice nulle de ![]() est dans
est dans ![]() qui n’est donc pas vide ;
qui n’est donc pas vide ;![]() soit
soit ![]() alors, pour tout
alors, pour tout ![]() et
et ![]() .
.
Donc ![]()
Bilan : ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() .
.
b/ Soit ![]() qui à toute matrice
qui à toute matrice ![]() de
de ![]() associe la matrice
associe la matrice ![]() . L’action de
. L’action de ![]() consiste à supprimer la dernière ligne et la dernière colonne d’une matrice d’ordre
consiste à supprimer la dernière ligne et la dernière colonne d’une matrice d’ordre ![]() , on obtient une matrice d’ordre
, on obtient une matrice d’ordre ![]()
Soit ![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Phi\left(\lambda M+N\right)&=&\Phi\left(\lambda (m_{i,j})_{(i,j)\in [\![1,n]\!]^2}+(n_{i,j})_{(i,j)\in [\![1,n]\!]^2}\right) \\ &=&\Phi\left( (\lambda m_{i,j}+n_{i,j})_{(i,j)\in [\![1,n]\!]^2}\right) \\ &=&(\lambda m_{i,j}+n_{i,j})_{(i,j)\in [\![1,n-1]\!]^2} \\ &=&\lambda (m_{i,j})_{(i,j)\in [\![1,n-1]\!]^2}+(n_{i,j})_{(i,j)\in [\![1,n-1]\!]^2} \\ &=&\lambda\Phi(M)+\Phi(N). \\ \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-434e76f7248c6719e88e9cd070ba50ac_l3.png)
Donc ![]()
Montrons que ![]() est injective. Soit
est injective. Soit ![]() comme
comme ![]() alors, pour tout
alors, pour tout ![]() la
la ![]() ligne de
ligne de ![]() contient
contient ![]() termes nul donc le
termes nul donc le ![]() terme est nul aussi car la somme vaut 0.
terme est nul aussi car la somme vaut 0.
Il en va de même pour les ![]() premières colonnes, il reste le terme en position
premières colonnes, il reste le terme en position ![]() qui vaut 0 car tous les autres valent 0, finalement
qui vaut 0 car tous les autres valent 0, finalement ![]() est la matrice nulle d’ordre
est la matrice nulle d’ordre ![]()
Montrons que ![]() est surjective. Soit
est surjective. Soit ![]() Pour tout
Pour tout ![]() on pose
on pose ![]() de sorte que
de sorte que ![]()
Pour tout ![]() on pose
on pose ![]() de sorte que
de sorte que ![]()
Il reste à déterminer ![]() et à vérifier que
et à vérifier que ![]()
Pour cela on pose ![]()
On vérifie que 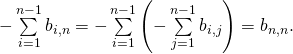
Ainsi la matrice ![]() est bien dans
est bien dans ![]() et elle est antécédent de
et elle est antécédent de ![]() par
par ![]()
![]() est donc surjective.
est donc surjective.
Bilan : ![]() est un isomorphisme de
est un isomorphisme de ![]() dans
dans ![]() donc la dimension de
donc la dimension de ![]() est celle de
est celle de ![]() donc
donc ![]() .
.
14/ On désire montrer que les matrices de permutation sont les seuls points extrémaux de ![]() .
.
On raisonne par récurrence sur ![]() . On note
. On note ![]() la proposition :
la proposition :
![]() : Si
: Si ![]() est un point extrémal de
est un point extrémal de ![]() , alors
, alors ![]() est une matrice de permutation.
est une matrice de permutation.
a/ La question 4 montre que dans ![]() seuls
seuls ![]() et
et ![]() sont extrémaux et ce sont les seules matrices de permutation de
sont extrémaux et ce sont les seules matrices de permutation de ![]()
On considère un entier naturel ![]() tel que
tel que ![]() soit réalisé et on se donne une matrice
soit réalisé et on se donne une matrice ![]() \\telle que
\\telle que ![]() est un point extrémal de
est un point extrémal de ![]() .
.
On suppose d’abord que la matrice ![]() a au moins
a au moins ![]() coefficients non nuls : il existe
coefficients non nuls : il existe ![]() couples
couples ![]() deux à deux distincts tels que
deux à deux distincts tels que ![]() est non nul.
est non nul.
On pose alors ![]() où les matrices
où les matrices ![]() sont les matrices élémentaires de la base canonique de
sont les matrices élémentaires de la base canonique de ![]() , c’est-à-dire que
, c’est-à-dire que ![]() est la matrice dont tous les coefficients sont nuls, à l’exception du coefficient d’indices
est la matrice dont tous les coefficients sont nuls, à l’exception du coefficient d’indices ![]() qui vaut 1.
qui vaut 1.
b/ On sait que ![]() et
et ![]() sont des sous-espaces de
sont des sous-espaces de ![]() donc
donc
![]()
En effet ![]() est de dimension
est de dimension ![]() car il a une famille génératrice à
car il a une famille génératrice à ![]() vecteurs qui est libre car sous-famille d’une base.
vecteurs qui est libre car sous-famille d’une base.
Or ![]() donc
donc ![]() donc
donc ![]() .
.
Bilan : ![]() .
.
c/ On prend ![]() non nul dans
non nul dans ![]() et pour tout réel
et pour tout réel ![]() , on note
, on note ![]() . On peut remarquer que, pour tout
. On peut remarquer que, pour tout ![]() car
car ![]() est dans
est dans ![]() et
et ![]() est dans
est dans ![]()
De même ![]() .
.
Il reste à trouver ![]() tel que
tel que ![]()
On pose ![]() Comme l’ensemble
Comme l’ensemble ![]() est non vide, fini et inclus dans
est non vide, fini et inclus dans ![]() , il a un minimum que l’on note
, il a un minimum que l’on note ![]()
On sait que ![]() est dans
est dans ![]() et qu’il est non nul donc il existe des scalaires
et qu’il est non nul donc il existe des scalaires ![]() non tous nul tels que
non tous nul tels que
![Rendered by QuickLaTeX.com \[N=\sum\limits_{k=1}^{2n} a_{k}E_{i_k,j_k}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c874660d584f409ef13d111f824d618f_l3.png)
On note ![]() , ce
, ce ![]() existe car l’ensemble est fini et
existe car l’ensemble est fini et ![]() car il y a au moins un terme strictement positif.
car il y a au moins un terme strictement positif.
On pose ![]() Soit un réel
Soit un réel ![]() prenons
prenons ![]()
Si ![]() alors
alors ![]()
Sinon soit ![]()
![]() , comme
, comme ![]() , on a
, on a ![]() on multiplie par
on multiplie par ![]() ainsi
ainsi ![]()
Or ![]() donc
donc ![]() de sorte que
de sorte que ![]() donc
donc
![]() et
et ![]()
Or ![]() est le minimum de
est le minimum de ![]() donc
donc ![]() .
.
Finalement pour tout ![]()
![]() .
.
d/ En considérant ![]() et
et ![]() comme
comme ![]() on a
on a ![]() et
et ![]() ,
,
de plus
![]()
Donc ![]() n’est pas extrémal dans
n’est pas extrémal dans ![]()
On aboutit à une contradiction : on a donc prouvé que la matrice ![]() a au plus
a au plus ![]() coefficicents non nuls.
coefficicents non nuls.
e/ La somme des coefficients de chaque colonne de ![]() vaut 1 donc il y a au moins un terme non nul dans chaque colonne de
vaut 1 donc il y a au moins un terme non nul dans chaque colonne de ![]() Cela représente
Cela représente ![]() termes. Il en reste au plus
termes. Il en reste au plus ![]() non nul, comme il y a
non nul, comme il y a ![]() colonnes, il y a au moins une colonne sans deuxième terme non nul.
colonnes, il y a au moins une colonne sans deuxième terme non nul.
Bilan : il existe une colonne de ![]() n’ayant qu’un seul terme non nul, et que ce terme vaut 1.
n’ayant qu’un seul terme non nul, et que ce terme vaut 1.
On note ![]() l’indice d’une telle colonne et
l’indice d’une telle colonne et ![]() l’indice tel que
l’indice tel que ![]() .
.
f/ On sait que la somme des coefficients de la ligne ![]() vaut 1 or
vaut 1 or ![]() donc s’il y a un autre terme non nul, il est forcément strictement positif et
donc s’il y a un autre terme non nul, il est forcément strictement positif et ![]() . C’est absurde.
. C’est absurde.
Bilan : la ligne d’indice ![]() de
de ![]() a tous ses coefficients nuls sauf
a tous ses coefficients nuls sauf ![]() .
.
g/ On considère alors la matrice ![]() obtenue à partir de
obtenue à partir de ![]() en lui enlevant la colonne d’indice
en lui enlevant la colonne d’indice ![]() et la ligne d’indice
et la ligne d’indice ![]() .
.
On a ![]() d’ordre
d’ordre ![]()
Soit ![]() on a
on a ![]()
Soit ![]() on a
on a ![]()
Soit ![]() on a
on a ![]()
Soit ![]() on a
on a ![]()
Les coefficients de ![]() clairement positifs donc
clairement positifs donc ![]() .
.
Montrons que ![]() est un point extrémal de
est un point extrémal de ![]() . On se donne
. On se donne ![]() dans
dans ![]() tels que
tels que ![]()
On ajoute à ![]() une colonne à la position
une colonne à la position ![]() et une ligne à la position
et une ligne à la position ![]() en décalant les colonnes d’indices
en décalant les colonnes d’indices ![]() ou plus et les lignes d’indice
ou plus et les lignes d’indice ![]() ou plus. Cette colonne et cette ligne ne contiennent que des 0 sauf en position
ou plus. Cette colonne et cette ligne ne contiennent que des 0 sauf en position ![]() où le coefficient vaut 1. On note
où le coefficient vaut 1. On note ![]() cette matrice d’ordre
cette matrice d’ordre ![]()
On fait la même chose sur ![]() , on note
, on note ![]() la nouvelle matrice. On vérifie facilement que
la nouvelle matrice. On vérifie facilement que ![]() et
et ![]() sont dans
sont dans ![]() Il suffit de reprendre la méthode du début de cette question. Par somme on remarque que
Il suffit de reprendre la méthode du début de cette question. Par somme on remarque que ![]() Or, par hypothèse,
Or, par hypothèse, ![]() est extrémal dans
est extrémal dans ![]() donc
donc ![]() Donc
Donc ![]()
Bilan : ![]() est un point extrémal de
est un point extrémal de ![]()
h/ On a supposé que ![]() est réalisé, comme
est réalisé, comme ![]() est un point extrémal de
est un point extrémal de ![]() , on peut dire que
, on peut dire que ![]() est une matrice de permutation de
est une matrice de permutation de ![]() .
.
Donc ![]() ne contient que des 0 et des 1 et en ajoutant la colonne et la ligne pour reconstruire
ne contient que des 0 et des 1 et en ajoutant la colonne et la ligne pour reconstruire ![]() on voit que
on voit que ![]() ne contient que des 0 et des 1 et comme
ne contient que des 0 et des 1 et comme ![]() est dans
est dans ![]() , on peut affirmer que
, on peut affirmer que ![]() est une matrice de permutation de
est une matrice de permutation de ![]() . Donc
. Donc ![]() est réalisé. Cela termine la preuve par récurrence.
est réalisé. Cela termine la preuve par récurrence.

