Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet HEC Maths 1 ECS 2016
Revenir à tous les corrigés des annales maths BCE
Partie I. Partitions de l’identité
1/ a/ ![]() est une matrice triangulaire, donc ses valeurs propres sont ses coefficients diagonaux, donc
est une matrice triangulaire, donc ses valeurs propres sont ses coefficients diagonaux, donc
![]()
![]() a une colonne nulle et deux colonnes non proportionnelles, donc
a une colonne nulle et deux colonnes non proportionnelles, donc ![]()
Donc, par le théorème du rang, ![]()
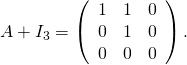 Et de même
Et de même ![]()
![]()
![]() admet deux valeurs propres et
admet deux valeurs propres et ![]()
donc ![]() donc
donc
![]()
b/ Après calculs, on trouve :  et
et  donc
donc ![]()
donc
![]()
c/ Supposons qu’il existe un polynôme ![]() de degré
de degré ![]() et annulateur de
et annulateur de ![]()
On note ![]() avec
avec ![]()
![]() donc
donc ![]() donc
donc 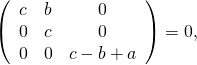 donc
donc ![]()
Contradiction puisque ![]()
Donc
![]()
d/ ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]() , donc de
, donc de ![]()
Donc ![]() donc
donc ![]()
En prenant ![]() et
et ![]()
donc ![]() et
et ![]()
on a bien ![]() ,
, ![]() et
et ![]()
Donc
![]()
2/ a/ ![]() est diagonalisable, donc
est diagonalisable, donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$E=\bigoplus\limits_{i=1}^{k}E_{\lambda _{i}}\left( f\right) .$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-65a8487e8da924fc221f001ded12c49d_l3.png)
Pour la suite de la question, on pose ![]()
Soit ![]() Alors
Alors ![]()
Soit alors ![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} Q\left( f\right) \left( x_{i}\right) &=&\left[\bigodot\limits_{j=1}^{k}\left( f-\lambda _{j}Id_{E}\right) \right] \left(x_{i}\right) \\ &=& \left[ \left( \bigodot\limits_{\substack{ 1\leqslant j\leqslant k \\ j\neq i }} \left( f-\lambda _{j}Id_{E}\right) \right) \circ \left(f-\lambda _{i}Id_{E}\right) \right] \left( x_{i}\right) \\ & =& \left( \bigodot\limits_{\substack{ 1\leqslant j\leqslant k \\ j\neq i } }\left( f-\lambda _{j}Id_{E}\right) \right) \underset{=0\text{ car }x_{i}\in E_{\lambda _{i}}\left( f\right) }{\underbrace{\left( f\left(x_{i}\right) -\lambda _{i}x_{i}\right) }} \\ &=&\left( \bigodot\limits_{\substack{1\leqslant j\leqslant k \\ j\neq i }} \left( f-\lambda _{j}Id_{E}\right)\right) \left( 0_{E}\right) \\ \end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-56cceb2e11399778f1cab9cba046c544_l3.png)
Donc ![]()
Donc, par linéarité de ![]()
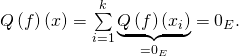
Donc ![]() donc
donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$Q=\prod\limits_{j=1}^{k}\left( X-\lambda _{j}\right) $ est un polyn\^ome annulateur de $f.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-daf6cb161ef120a7273e8b142e0702b1_l3.png)
b/ Soit ![]()
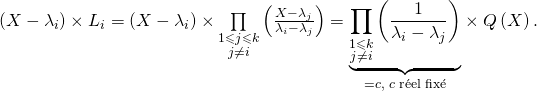
Donc ![]() car
car ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]()
Donc ![]() donc
donc ![]()
Donc
![]()
c/ ![]() Soit
Soit ![]()
![]() est donné sous forme factorisée, donc les racines de
est donné sous forme factorisée, donc les racines de ![]() sont les réels
sont les réels ![]()
![]()
Et on a clairement ![]()
Donc ![]() .
.
![]() Soit
Soit ![]()
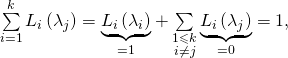 donc
donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$\sum\limits_{i=1}^{k}L_{i}\left(\lambda _{j}\right) =1.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-778af7999c19454dc5e7c77a32e465dc_l3.png)
![]() Soit
Soit ![]()
![]() , donc
, donc ![]()
Soit ![]()
Ou bien ![]() . Alors
. Alors ![]() est vecteur propre de
est vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() donc
donc ![]() est vecteur propre de
est vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() donc
donc ![]()
Ou bien ![]() et alors la formule précédente est clairement vraie.
et alors la formule précédente est clairement vraie.
D’où ![]()
Soit ![]()

On pose ![]()
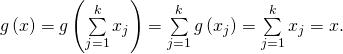
Donc ![]() donc
donc ![]()
et
![]()
d/ 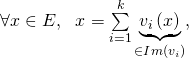 donc
donc ![]() L’inclusion inverse étant claire, on a
L’inclusion inverse étant claire, on a
![Rendered by QuickLaTeX.com \[\fbox{\text{$E=\sum\limits_{i=1}^{k}\func{Im}\left(v_{i}\right) .$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e64b4efca85bf032661220a263407fe4_l3.png)
Or ![]() donc
donc ![]()
donc ![]()
Comme ![]() la somme
la somme ![]() est directe aussi
est directe aussi
et ![]()
Notons alors, pour ![]() et
et ![]()
On a donc ![]() donc
donc 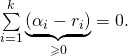
Or une somme de termes positifs est nulle si et seulement si chacun des termes de la somme est nulle, donc ![]()
Et comme on a toujours ![]() on en déduit que
on en déduit que
![]()
Soit ![]() On a toujours
On a toujours ![]() Donc
Donc ![]() où
où ![]()
On note ![]()
On a ![]() et
et ![]()
donc ![]()
De plus, ![]()
Et 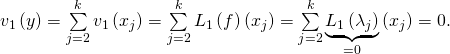
Donc, ![]()
donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$v_{1}$ est le projecteur sur $\func{Im}\left( v_{1}\right)=E_{\lambda _{1}}\left( f\right) $ parall\`element à $F=\bigoplus\limits_{j=2}^{k}E_{\lambda _{j}}\left( f\right) .$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d84acc9caea49c5285cf8db5e0fadc77_l3.png)
3/ a/ On a ![]() donc
donc 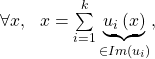 donc
donc ![]() L’inclusion inverse
L’inclusion inverse
étant claire, on a
![Rendered by QuickLaTeX.com \[\fbox{\text{$E=\sum\limits_{i=1}^{k}\func{Im}\left(u_{i}\right) .$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d18a6d5edc29bbd689b26234c2925975_l3.png)
On note, pour ![]()
![]() une base de
une base de ![]()
On note ![]() la concaténation des
la concaténation des ![]()
Soit ![]()
![]() donc
donc ![]() tel que
tel que ![]()
Or pour tout ![]() est combinaison des éléments de
est combinaison des éléments de ![]() (puisque
(puisque ![]() est une base de
est une base de ![]() ),
),
donc ![]() est combinaison linéaire des éléments de
est combinaison linéaire des éléments de ![]() (puisque
(puisque ![]()
Donc ![]() est combinaison linéaire des éléments de
est combinaison linéaire des éléments de ![]()
On en déduit que ![]() est une famille génératrice de
est une famille génératrice de ![]() donc
donc 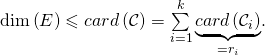
Donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$n\leqslant \sum\limits_{i=1}^{k}r_{i}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8cbaeec8562d4a5a33b6fbf848ebc9ba_l3.png)
b/ On a ![]() Donc par le cours,
Donc par le cours,
![Rendered by QuickLaTeX.com \[\fbox{\text{$E=\bigoplus\limits_{i=1}^{k}\func{Im}\left( u_{i}\right) $ ssi $n=\sum\limits_{i=1}^{k}r_{i.}$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ed9c8cdd003c4bf6c10a995e0885598c_l3.png)
c/ ![]() On suppose que les endomorphismes
On suppose que les endomorphismes ![]() sont des projecteurs.
sont des projecteurs.
Soit ![]() On note,
On note, ![]()
![]() est un projecteur, donc
est un projecteur, donc ![]() où
où 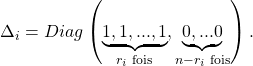
(Éventuellement, on peut avoir ![]() ou
ou ![]() ).
).
Deux matrices semblables ayant même trace, on a ![]()
![]() forment une partition de l’identité de
forment une partition de l’identité de ![]() donc
donc ![]() donc
donc ![]()
D’où : ![]() par linéarité de la trace. Donc
par linéarité de la trace. Donc ![]()
On a donc bien
![]()
![]() On suppose que
On suppose que ![]()
Donc d’après la question 3.b/, ![]()
Soit ![]() Soit
Soit ![]()
On a ![]() et
et ![]()
d’où :
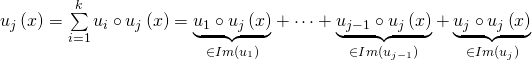
![]()
Or ![]() donc par unicité de la décomposition, on a
donc par unicité de la décomposition, on a ![]()
Donc pour tout ![]() tel que
tel que ![]()
![]() donc
donc ![]()
On a donc bien
![]()
![]() On suppose que pour tout
On suppose que pour tout ![]() tel que
tel que ![]()
![]()
Soit ![]()
![]() donc
donc 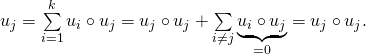
Donc ![]() donc
donc ![]() est un projecteur.
est un projecteur.
Donc on a bien ![]()
Et on a montré que ![]()
![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie II. Représentation matricielle d’un projecteur orthogonal
4/ a/ D’après le cours, ![]() est un projecteur orthogonal ssi
est un projecteur orthogonal ssi ![]() est un projecteur et un endomorphisme symétrique.
est un projecteur et un endomorphisme symétrique.
![]()
![]() est un projecteur ssi
est un projecteur ssi ![]() ssi
ssi ![]()
![]()
![]() est une base orthonormée et
est une base orthonormée et ![]()
D’où : ![]() est un endomorphisme symétrique ssi
est un endomorphisme symétrique ssi ![]()
Donc
![]()
b/ ![]() Supposons qu’il existe
Supposons qu’il existe ![]() réel et
réel et ![]() projecteur orthogonal tel que
projecteur orthogonal tel que ![]() .
.
On note ![]()
![]() par linéarité de la trace.
par linéarité de la trace.
Donc ![]() car
car ![]() est un projecteur.
est un projecteur.
De même ![]()
Donc ![]()
De plus ![]() car
car ![]() est un projecteur orthogonal, donc
est un projecteur orthogonal, donc ![]()
![]() Supposons que
Supposons que ![]() et
et ![]()
Ou bien ![]() On pose
On pose ![]() donc
donc ![]()
Or ![]() est symétrique, donc
est symétrique, donc ![]()
Donc ![]() Or
Or ![]() et une somme de termes positifs est nulle si et seulement si chacun de ses termes est nul, donc
et une somme de termes positifs est nulle si et seulement si chacun de ses termes est nul, donc ![]()
Donc ![]() et en prenant
et en prenant ![]() et
et ![]() on a bien
on a bien ![]() avec
avec ![]() projecteur orthogonal.
projecteur orthogonal.
Ou bien ![]() Alors
Alors ![]() donc
donc ![]() ou
ou ![]() et on est ramené au cas précédent.
et on est ramené au cas précédent.
Ou bien ![]() et
et ![]() .
.
Alors on pose ![]() ,
, ![]() et
et ![]() l’endomorphisme de
l’endomorphisme de ![]() de matrice
de matrice ![]() dans la base
dans la base ![]()
On a bien ![]() et
et ![]() car
car ![]() réel et
réel et ![]()
D’autre part 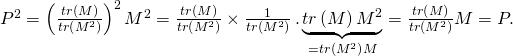
![]() et
et ![]() donc
donc ![]() est un projecteur orthogonal (par 4.a), et on a bien trouvé
est un projecteur orthogonal (par 4.a), et on a bien trouvé ![]() et
et ![]() projecteur orthogonal tels que
projecteur orthogonal tels que ![]()
5/ a/
function t=tr(![]() ) (on entre une matrice carrée)
) (on entre une matrice carrée)
![]()
![]()
![]()
![]()
![]()
![]()
b/ Signification de la ligne ![]() . On note
. On note ![]()
On affecte à ![]() la valeur
la valeur ![]() si
si ![]() contient déjà
contient déjà ![]()
![]()
![]()
Donc tant que les coefficients ![]() et
et ![]() sont égaux,
sont égaux, ![]() reçoit
reçoit ![]() et si à un moment on a
et si à un moment on a ![]() alors
alors ![]() reçoit
reçoit ![]() Dans ce dernier cas,
Dans ce dernier cas, ![]() garde la valeur
garde la valeur ![]() jusqu’à la fin des deux boucles, car
jusqu’à la fin des deux boucles, car ![]() et
et ![]()
![]()
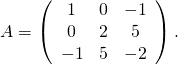
![]() est initialisé à
est initialisé à ![]()
Pour ![]()
Pour ![]()
![]() est
est ![]()
![]()
![]() est
est ![]() donc
donc ![]() garde la valeur
garde la valeur ![]()
Pour ![]()
![]() est
est ![]()
![]()
![]() est
est ![]() donc
donc ![]() garde la valeur
garde la valeur ![]()
De même pour ![]() Et
Et ![]() aura la valeur
aura la valeur ![]() à la fin de la fonction, ce qui est bien cohérent avec le fait que
à la fin de la fonction, ce qui est bien cohérent avec le fait que ![]() est symétrique.
est symétrique.
![]()
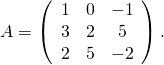
![]() est initialisé à
est initialisé à ![]()
Pour ![]()
Pour ![]()
![]() est
est ![]() \textbf{et }
\textbf{et }![]() est
est ![]() donc
donc ![]() prend la valeur
prend la valeur ![]()
Pour ![]() est
est ![]() , donc peu importe la valeur de
, donc peu importe la valeur de ![]() donc
donc ![]() garde la
garde la
valeur ![]()
De même pour ![]() Et
Et ![]() aura la valeur
aura la valeur ![]() à la fin de la fonction.
à la fin de la fonction.
c/ Il reste à tester si ![]() c’est-à dire si
c’est-à dire si ![]()
Dans l’instruction ![]() on n’effectue le
on n’effectue le ![]() que si
que si ![]() est
est ![]() c’est-à dire si
c’est-à dire si ![]() est symétrique. On a alors
est symétrique. On a alors ![]() et
et ![]() symétriques, donc il suffit de tester si les termes des triangles supérieurs de
symétriques, donc il suffit de tester si les termes des triangles supérieurs de ![]() et
et ![]()
![]() sont égaux pour savoir si
sont égaux pour savoir si ![]() et
et ![]() sont égaux.
sont égaux.
La ligne manquante est : ![]()
![]()
![]()
![]() est bien symétrique. Après calculs
est bien symétrique. Après calculs ![]() et
et ![]()
donc ![]()
![]()
![]()
![]() est bien symétrique. Après calculs
est bien symétrique. Après calculs ![]() donc
donc ![]()
6/ a/ Supposons ![]() Alors
Alors ![]() donc
donc ![]() donc
donc ![]()
Supposons ![]() Alors
Alors ![]() donc
donc ![]() donc
donc ![]()
On considère alors le produit scalaire canonique sur ![]() on a donc
on a donc ![]()
Donc ![]() et
et ![]()
On a donc montré que
![]()
On a ![]() et
et ![]() Notons
Notons ![]() l’endomorphisme de
l’endomorphisme de ![]() canoniquement associé à
canoniquement associé à ![]() et
et ![]() l’application linéaire de
l’application linéaire de ![]() dans
dans ![]() canoniquement associée à
canoniquement associée à ![]()
![]() est donc l’ensemble de départ des deux applications linéaires
est donc l’ensemble de départ des deux applications linéaires ![]() et
et ![]()
Alors, par le théorème du rang,
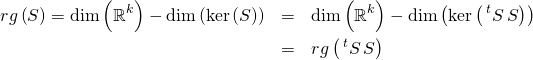
Donc
![]()
b/ On note, pour ![Rendered by QuickLaTeX.com j\in \left[ \!\left[ 1,k\right] \!\right],\,\,\,S_{j}=\left( \begin{array}{c}s_{1,j} \\ s_{2,j} \\ \vdots \\ s_{n,j}\end{array}\right) .](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3591088a52fe8bee8f49cd8dc417de32_l3.png)
Soit ![]()
![]()
![]()
![]()
![]()
![]()
![]() (On a posé
(On a posé  ).
).
Donc
![]()
c/ ![]()
Or ![]()
![]()
![]() (expression du produit scalaire dans la base orthonormée
(expression du produit scalaire dans la base orthonormée ![]() )
)
![]()
![]()
![]() (en transposant)
(en transposant)
Donc
![]()
d/ Soit ![]() et
et ![]()
![]() donc
donc ![]() donc
donc ![]()
![]() donc
donc ![]() donc
donc ![]() donc
donc ![]()
Donc
![]()
e/ On suppose que ![]() est libre.
est libre.
Donc ![]() et par la question a),
et par la question a), ![]()
Or ![]() donc
donc ![]() est inversible.
est inversible.
De plus, d’après d/ ![]() et
et ![]()
donc ![]() et
et ![]()
![]()
donc ![]()
![]()
Donc
![]()
7/ a/ ![]() est une matrice symétrique réelle, donc est diagonalisable dans une base orthonormée de vecteurs propres, et il existe une matrice
est une matrice symétrique réelle, donc est diagonalisable dans une base orthonormée de vecteurs propres, et il existe une matrice ![]() orthogonale et une matrice
orthogonale et une matrice ![]() diagonale telles que
diagonale telles que ![]() On note
On note ![]() Donc
Donc
![]()
b/ On a :
![]()
car ![]() est une matrice orthogonale.
est une matrice orthogonale.
Donc ![]()
Or pour ![]()
![]()
Donc pour ![]()
![]() donc
donc
![]()
De même, ![]()
et pour ![Rendered by QuickLaTeX.com i\in \left[ \!\left[ 1,k\right] \!\right] ,\left( h\left( \rho_{i}\right) \right) ^{2}\rho _{i}=\left\{ \begin{array}{l}\rho _{i}\times \frac{1}{\rho _{i}^{2}}\text{ si }\rho _{i}\neq 0 \\ 0\text{ si }\rho _{i}=0\end{array}\right. =\left\{ \begin{array}{l}\frac{1}{\rho _{i}}\text{ si }\rho _{i}\neq 0 \\ 0\text{ si }\rho _{i}=0\end{array}\right. =h\left( \rho _{i}\right) .](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0ce780310945497346114cc5cb60f95f_l3.png)
Donc
![]()
![]()
![]()
![]()
Donc,
![]()
![]()
Car une matrice diagonale est symétrique.
Donc
![]()
On prouve de même que
![]()
Et on a bien montré que ![]() est une inverse de Penrose-Moore de
est une inverse de Penrose-Moore de ![]()
c/ ![]()
![]() car
car ![]() est symétrique.
est symétrique.
Donc
![]()
![]()
Or ![]() est symétrique, donc
est symétrique, donc ![]()
Et en utilisant à nouveau le fait que ![]() est symétrique, on a
est symétrique, on a
![]()
![]() On supose que
On supose que ![]() On note
On note ![]() les colonnes de
les colonnes de ![]()
Alors, pour tout ![]()
Donc ![]()
![]() car
car ![]() est symétrique, donc
est symétrique, donc ![]() donc
donc ![]()
Et en utilisant le produit scalaire canonique sur ![]() on a
on a ![]() donc
donc ![]()
Donc ![]() donc
donc
![]()
![]() On pose
On pose ![]()
On a d’après ![]() car
car ![]() et
et ![]() sont des inverses de Penrose-Moore,
sont des inverses de Penrose-Moore, ![]()
![]() Donc
Donc ![]() donc d’après
donc d’après ![]()
![]()
donc ![]() .
.
De plus, en reprenant le même type de calculs qu’au ![]()
![]() car
car ![]() est symétrique.
est symétrique.
Et en prenant ![]() on trouve de même que ci-dessus,
on trouve de même que ci-dessus, ![]()
Donc ![]()
Donc ![]() . Donc
. Donc
![]()
Donc si ![]() est une inverse de Penrose-Moore de
est une inverse de Penrose-Moore de ![]() , alors
, alors ![]() est unique et
est unique et ![]()
On a montré au a) que ![]() était une inverse de Penmore-Moore de
était une inverse de Penmore-Moore de ![]() .
.
Donc
![]()
8/ a/ Résultat préliminaire : soit ![]() et
et ![]()
On a ![]() donc
donc ![]()
Une matrice et sa transposée ayant même rang, on a
![]()
Donc ![]() et
et ![]()
Ici, 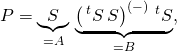 donc
donc ![]()
De plus, ![]() , donc
, donc ![]() par définition de
par définition de ![]() au début du 15.
au début du 15.
Donc ![]() donc
donc ![]() d’après 14.a), donc
d’après 14.a), donc ![]()
De plus, d’après le résultat préliminaire, ![]()
Donc ![]()
Donc
![]()
b/ En utilisant les propriétés de ![]() on montre que
on montre que ![]() et que
et que ![]() donc que
donc que ![]() est la matrice d’un projecteur orthogonal que l’on note
est la matrice d’un projecteur orthogonal que l’on note ![]() .
.
D’après 14.c/ pour ![]() On a
On a ![]() donc
donc ![]() donc
donc ![]()
Or ![]() Donc
Donc ![]()
Donc
![]()
9/ a/ On sait que ![]() Or
Or ![]() et
et ![]() n’est pas inversible, donc
n’est pas inversible, donc ![]() donc
donc ![]() et
et ![]() est une famille liée.
est une famille liée.
Comme ![]()
![]() donc
donc
![]()
b/ On a :
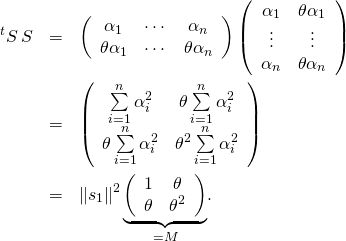
Les deux colonnes de ![]() sont proportionnelles, donc
sont proportionnelles, donc ![]() n’est pas inversible, et
n’est pas inversible, et ![]() est valeur propre de
est valeur propre de ![]() Un vecteur propre associée est, par exemple,
Un vecteur propre associée est, par exemple, ![]()
![]() est symétrique réelle, donc diagonalisable dans une base orthonormée de vecteurs propres et il existe
est symétrique réelle, donc diagonalisable dans une base orthonormée de vecteurs propres et il existe ![]() orthogonale et
orthogonale et ![]() diagonale telles que
diagonale telles que ![]()
On pose, par exemple, ![]()
![]() et
et ![]() sont semblables, donc ont même trace, donc
sont semblables, donc ont même trace, donc ![]() donc
donc ![]()
Un vecteur propre associé à ![]() est, par exemple,
est, par exemple, ![]()
La famille ![]() est donc une famille de vecteurs propres, clairement orthonormée. Elle est donc libre, de cardinal
est donc une famille de vecteurs propres, clairement orthonormée. Elle est donc libre, de cardinal ![]() et comme
et comme ![]() c’est une base orthonormée de
c’est une base orthonormée de ![]()
Donc, en posant ![]() on a bien
on a bien ![]()
Donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$Q=\frac{1}{\sqrt{1+\theta ^{2}}}\left( \begin{array}{cc}1 & \theta \\ \theta & -1\end{array}\right) $ est telle que $^{t}Q\,^{t}S\,S\,Q$ est diagonale.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cf508ba362fd993563178160d349a4e7_l3.png)
c/ D’après la question 7/ b/, on a :
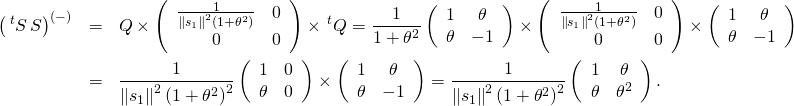
Donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$\left( \,^{t}S\,S\right) ^{\left( -\right) }=\frac{1}{\left\|s_{1}\right\| ^{2}\left( 1+\theta ^{2}\right) ^{2}}\left( \begin{array}{cc}1 & \theta \\ \theta & \theta ^{2}\end{array}\right) .$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1c69ad52a497e433021b7d588c426185_l3.png)
d/ On reprend les notations de la question 8, et on note ![]() la matrice de
la matrice de ![]() dans la base
dans la base ![]()
On a donc
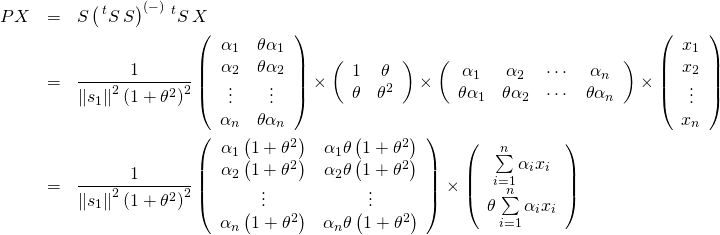
Donc 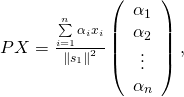 donc
donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$p_{F}\left( x\right) =\frac{\sum\limits_{i=1}^{n}\alpha _{i}x_{i}}{\left\| s_{1}\right\| ^{2}}.s_{1}=\frac{\left\langle s_{1},x\right\rangle }{\left\| s_{1}\right\| ^{2}}s_{1}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2a1e9e48c0e46ebe4f97e2ed57f79fa9_l3.png)
… et on retrouve la formule du cours, car ![]() puisque
puisque ![]() est liée et
est liée et ![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie III : densité et gaussienne centrée
10/ ![]() Soit
Soit ![]()
![]() donc
donc ![]()
![]() Soit
Soit ![]() une variable aléatoire qui suit la loi
une variable aléatoire qui suit la loi ![]() On note
On note ![]() sa fonction de répartition et
sa fonction de répartition et ![]() sa densité usuelle.
sa densité usuelle.
On note ![]()
On a ![]() donc, pour
donc, pour ![]()
Pour ![]()
![]()
![]()
Or ![]() est de classe
est de classe ![]() sur
sur ![]()
De plus ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() à valeurs dans
à valeurs dans ![]() donc
donc ![]() est de classe
est de classe ![]() sur
sur ![]()
![]() étant nulle sur
étant nulle sur ![]() on a aussi
on a aussi ![]() est de classe
est de classe ![]() sur
sur ![]()
Enfin ![]() ,
, ![]() et
et ![]() car
car ![]() est continue en
est continue en ![]() et
et ![]() tend vers
tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() donc
donc ![]() est continue en
est continue en ![]()
![]() est donc continue sur
est donc continue sur ![]() et de classe
et de classe ![]() sur
sur ![]() sauf en
sauf en ![]() donc
donc
![]()
On obtient une densité de ![]() en dérivant
en dérivant ![]() sur
sur ![]() et en donnant une valeur arbitraire positive à
et en donnant une valeur arbitraire positive à ![]()
Donc une densité ![]() est donnée par :
est donnée par :
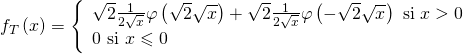
D’où : 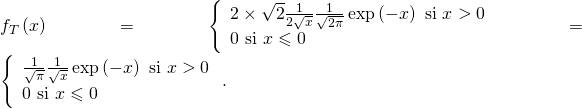
Donc 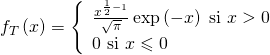
![]() étant une densité, on a
étant une densité, on a ![]() donc
donc ![]()
Donc, on a ![]()
![]()
Donc ![]() et on trouve :
et on trouve :
![Rendered by QuickLaTeX.com \[\fbox{\text{$f_{T}\left( x\right) =\left\{ \begin{array}{l}\frac{x^{\left( \frac{1}{2}-1\right) }}{\,\Gamma \left( \frac{1}{2}\right) }\exp \left( -x\right) \text{ si }x>0 \\ 0\text{ si }x\leqslant 0\end{array}\right. $}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ad7b03f379d6eb205a0d436a9a7b96a3_l3.png)
![]()
![]() On note, pour
On note, pour ![]()
![]() Comme
Comme ![]() on sait que
on sait que ![]() par le point précédent
par le point précédent![]()
Les variables ![]() sont indépendantes (par le lemme des coalitions car les
sont indépendantes (par le lemme des coalitions car les ![]() le sont), et toutes de loi
le sont), et toutes de loi ![]()
Donc, par stabilité de la loi ![]()
![]() suit la loi
suit la loi ![]() donc
donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$\frac{1}{2}\sum\limits_{i=1}^{n}\left( \frac{X_{i}-\mu }{\sigma }\right)^{2}\hookrightarrow \gamma \left( \frac{n}{2}\right) .$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e23894488c4009f617192010dab34162_l3.png)
donc
![Rendered by QuickLaTeX.com \[\fbox{\text{$\sum\limits_{i=1}^{n}\left( \frac{X_{i}-\mu }{\sigma }\right)^{2}\hookrightarrow \chi ^{2}\left( n\right) .$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8f6535fec2f7c7fb2a590faf631036ec_l3.png)
11/ a/ On pose ![]()
![]() donc pour
donc pour ![]()
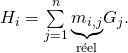
![]() est un vecteur gaussien, donc par définition, pour
est un vecteur gaussien, donc par définition, pour ![]()
![]() est une variable gaussienne centrée.
est une variable gaussienne centrée.
Soit alors ![]() dans
dans ![]()
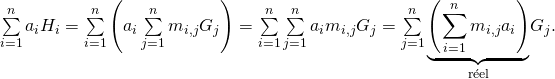
![]() est un vecteur gaussien, donc par définition,
est un vecteur gaussien, donc par définition, ![]() est une variable gaussienne centrée.
est une variable gaussienne centrée.
Donc
![]()
b/ Pour tout ![]()
![]() admet un moment d’ordre
admet un moment d’ordre ![]() donc d’après le cours,
donc d’après le cours,
![]()
12/ a/ Soit ![]()
Si ![]() alors
alors ![]() et
et ![]() est une gaussienne centrée.
est une gaussienne centrée.
On suppose ![]() pour la suite du raisonnement.
pour la suite du raisonnement.
Soit ![]()
![]() ou bien
ou bien ![]() Alors
Alors ![]() (stabilité par transformation affine de la loi normale).
(stabilité par transformation affine de la loi normale).
![]() ou bien
ou bien ![]() Alors
Alors ![]() est la variable constante nulle.
est la variable constante nulle.
On note ![]()
![]() car
car ![]()
Les variables ![]() sont indépendantes et toutes de loi normale, donc, par stabilité de la loi normale,
sont indépendantes et toutes de loi normale, donc, par stabilité de la loi normale, ![]()
Or ![]() car on rajoute des variables constantes nulles et
car on rajoute des variables constantes nulles et ![]() car on rajoute des termes nuls,
car on rajoute des termes nuls,
donc ![]()
Donc ![]() est une gaussienne centrée.
est une gaussienne centrée.
Donc pour tout ![]() est une gaussienne centrée,
est une gaussienne centrée,
donc
![]()
Soit ![]() avec
avec ![]()
![]() car
car ![]() et
et ![]() sont indépendantes.
sont indépendantes.
Donc ![]() car
car ![]()
Soit ![]() Alors
Alors ![]()
Donc
![]()
b/ On note ![]()
![]() donc par définition du produit matriciel, on a
donc par définition du produit matriciel, on a ![]()
![]() est orthogonale, donc
est orthogonale, donc ![]()
![]() Soit
Soit ![]()
![]() est un vecteur gaussien d’après la question précédente.
est un vecteur gaussien d’après la question précédente.
Donc ![]() est un vecteur gaussien d’après la question 11/ a/.
est un vecteur gaussien d’après la question 11/ a/.
En prenant ![]() avec
avec ![]() en
en ![]() position, on a
position, on a ![]() est une gaussienne centrée.
est une gaussienne centrée.
Or ![]()
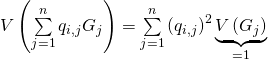 car les variables
car les variables ![]() sont mutuellement indépendantes.
sont mutuellement indépendantes.
Donc ![]() car on reconnaît un terme diagonal de
car on reconnaît un terme diagonal de ![]()
Donc
![]()
![]() Soit
Soit ![]()
![]()
![]()
![]() par linéarité de l’espérance
par linéarité de l’espérance
 d’après
d’après ![]()
![]()
On reconnaît le terme général de ![]()
Donc ![]() car
car ![]() est une matrice orthogonale.
est une matrice orthogonale.
Donc
![]()
Donc pour tout ![]()
![]()
![]() par indépendance des
par indépendance des ![]()
![]() car
car ![]() et
et ![]() ont même loi
ont même loi ![]() .
.
Donc
![]()
13/ a/ ![]() et
et ![]() donc d’après la question
donc d’après la question ![]()
![]() sont des matrices de projecteurs notés respectivement
sont des matrices de projecteurs notés respectivement ![]()
De plus, ![]() sont symétriques réelles et
sont symétriques réelles et ![]() est une base orthonormée, donc d’après la question 4.a),
est une base orthonormée, donc d’après la question 4.a),
![]()
Soit ![]() avec
avec ![]()
Soit ![]()
![]() car
car ![]() et
et ![]()
Donc ![]() car
car ![]() est un endomorphisme symétrique (sa matrice représentative dans la base
est un endomorphisme symétrique (sa matrice représentative dans la base ![]() orthonormée est symétrique réelle)
orthonormée est symétrique réelle)
Or ![]() d’après la question 3.c/ puisque
d’après la question 3.c/ puisque ![]() donc
donc ![]()
Donc
![]()
b/ D’après la question 3, on a ![]()
On note, pour ![]() une base orthonormée de
une base orthonormée de ![]() et
et ![]() la concaténation des
la concaténation des ![]()
![]() est donc une base orthonormée de
est donc une base orthonormée de ![]()
On note ![]() la matrice de passage de
la matrice de passage de ![]() à
à ![]()
![]() est la matrice de passage d’une base orthonormée à une base orthonormée, c’est donc une matrice orthogonale.
est la matrice de passage d’une base orthonormée à une base orthonormée, c’est donc une matrice orthogonale.
On note pour ![]()
Pour ![]()
![]() est le projecteur orthogonal sur
est le projecteur orthogonal sur ![]() Donc les vecteurs de
Donc les vecteurs de ![]() ont pour image eux-mêmes car ils sont dans
ont pour image eux-mêmes car ils sont dans ![]() , et les vecteurs de
, et les vecteurs de ![]() sont dans
sont dans ![]() d’après la question précédente, donc dans
d’après la question précédente, donc dans ![]()
Donc pour ![Rendered by QuickLaTeX.com i\in \left[ \!\left[ 1,k\right] \!\right] ,\Delta _{i}=Diag\left( \underset{r_{1}\text{ fois}}{\underbrace{0,...,0}},...,\underset{r_{i-1}\text{ fois}}{\underbrace{0,...,0}},\underset{r_{i}\text{ fois}}{\underbrace{1,...,1}},\underset{r_{i+1}\text{ fois}}{\underbrace{0,...,0}},...,\underset{r_{k}\text{ fois}}{\underbrace{0,...,0}}\right) .](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4de75d655af76cdfea3e50d78334b12f_l3.png)
Donc
![]()
c/ On suppose que ![]()
![]()
![]() est un vecteur gaussien et toutes les variables aléatoires ont une variance égale à
est un vecteur gaussien et toutes les variables aléatoires ont une variance égale à ![]() , donc avec la même démarche qu’à la question 12.a), on montre que
, donc avec la même démarche qu’à la question 12.a), on montre que ![]() suivent toutes la loi
suivent toutes la loi ![]()
On pose ![]()
![]() est une matrice orthogonale, et
est une matrice orthogonale, et ![]() sont mutuellement indépendantes et toutes de loi
sont mutuellement indépendantes et toutes de loi ![]() donc d’après la question 12.b/,
donc d’après la question 12.b/, ![]() sont mutuellement indépendantes et toutes de loi
sont mutuellement indépendantes et toutes de loi ![]()
De plus, ![]() et les variables aléatoires
et les variables aléatoires ![]() sont mutuellement indépendantes et toutes de loi
sont mutuellement indépendantes et toutes de loi ![]() donc, d’après la question 10, avec
donc, d’après la question 10, avec ![]() et
et ![]()
![]() Donc
Donc
![]()
d/ Avec les mêmes notations qu’au c/, on a
![]()
Or les variables ![]() sont mutuellement indépendantes, donc par le lemme des coalitions,
sont mutuellement indépendantes, donc par le lemme des coalitions,
![]()

