Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet HEC Maths 1 ECS 2019
Revenir à tous les corrigés des annales de maths BCE
Partie I. Un premier exemple
1/ Nous avons deux colonnes proportionnelles et non nulles donc ![]() .
.
![]() donc
donc ![]() et
et ![]() est un projecteur. Donc
est un projecteur. Donc ![]() est diagonalisable
est diagonalisable
Les valeurs propres de ![]() sont parmi
sont parmi ![]()
On constate que ![]() et
et ![]()
Donc ![]() et
et ![]() sont les valeurs propres de
sont les valeurs propres de ![]() et comme
et comme ![]() chacun des deux sous espaces
chacun des deux sous espaces
propres est de dimension ![]() .
.
En dimension finie, la famille libre est donc une base donc génératrice et
![]() et
et ![]()
2/ ![]()
![]()
![]() est une matrice symétrique réelle. Elle est donc diagonalisable
est une matrice symétrique réelle. Elle est donc diagonalisable
Si ![]() alors
alors ![]() donc
donc ![]() et
et ![]() donc
donc![]()
et ![]() de rang
de rang ![]() donc (th. du rang)
donc (th. du rang) ![]()
et ![]()
![]()
Et on a ![]()
![]()
![]() donc
donc ![]() vecteur propre associé à la valeur propre
vecteur propre associé à la valeur propre ![]()
En dimension ![]()
![]() ne peut pas avoir d’autre valeurs propres.
ne peut pas avoir d’autre valeurs propres.
Et la somme des dimension des sous espaces propres impose que
![]()
et ![]() .
.
3/ ![]() est la matrice d’un projecteur
est la matrice d’un projecteur ![]()
![]() est un projecteur
est un projecteur
Alors ses valeurs propres sont parmi ![]() donc
donc ![]() ou
ou ![]() (impossible)
(impossible)
Donc ![]() et quand
et quand ![]()
![]() donc
donc
![]() est la matrice d’un projecteur
est la matrice d’un projecteur ![]()
![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie II. Généralités
4/ a/ On a ![]()
et
![]()
4/ b/ On vérifie les propriétés d’un produit scalaire une à une :
![]() Application de
Application de ![]() dans
dans ![]()
![]() Symétrique car
Symétrique car ![]()
![]() Linéaire à droite par linéarité de la trace donc bilinéaire
Linéaire à droite par linéarité de la trace donc bilinéaire
![]() Positive :
Positive : ![]()
![]() Définie positive : si
Définie positive : si ![]() une somme de termes positifs est nulle alors
une somme de termes positifs est nulle alors
tous les termes sont nuls donc ![]() et
et ![]()
4/ c/ Cauchy-Schwarz :
![]() pour tout
pour tout ![]() et
et ![]() de
de ![]() ou encore
ou encore ![]()
On a ![]() avec
avec
![]()
donc ![]()
Et par le cas d’égalité dans l’inégalité de Cauchy-Schwarz,
![]()
![]()
![]() et
et ![]() sont colinéaires.
sont colinéaires.
et s’il existe ![]() tel que
tel que ![]() alors
alors ![]() et
et ![]()
Si ![]()
![]() donc
donc ![]()
et ![]() et
et ![]() est symétrique.
est symétrique.
Si ![]() alors
alors ![]() est symétrique
est symétrique
Donc, si ![]() alors
alors ![]()
Réciproquement, si ![]() on aura bien l’égalité.
on aura bien l’égalité.
Donc ![]()
5/ a/ ![]()
donc ![]() et
et ![]()
5/ b/ ![]() est une matrice de passage entre deux bases orthonormées.
est une matrice de passage entre deux bases orthonormées.
Ces colonnes sont les coordonnées des ![]() dans
dans ![]()
Donc, les produits scalaires valent (![]() colonne associée à
colonne associée à ![]() )
)
![]() si
si ![]() et
et ![]() si
si ![]()
Donc ![]()
5/ c/ ![]() donc
donc ![]()
et ![]()
Donc ![]() est la matrice de
est la matrice de ![]() dans la base
dans la base ![]() .
.
6/ a/ ![]() et comme c’est une matrice
et comme c’est une matrice
de ![]() ,
,
![]() .
.
6/ b/ Avec ![]() si
si ![]() alors
alors ![]() et
et ![]()
donc ![]()
donc ![]()
Réciproquement :
Si ![]() alors
alors ![]() donc
donc ![]() donc
donc ![]()
donc ![]() donc
donc ![]() donc
donc ![]() d’où
d’où![]()
et ![]()
6/ c/ ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
Sa matrice ![]() dans une base orthonormée est symétrique :
dans une base orthonormée est symétrique :
![]()
Donc ![]() est un endomorphisme symétrique de
est un endomorphisme symétrique de ![]()
6/ d/ Soit ![]() un vecteur propre de
un vecteur propre de ![]() associé à
associé à ![]()
Et ![]() la colonne de ses coordonnées dans
la colonne de ses coordonnées dans ![]() .
.
![]() donc
donc ![]() et
et ![]()
Comme ![]() alors
alors ![]()
6/ e/ ![]() symétrique est diagonalisable sur une base orthonormée de vecteurs propres.
symétrique est diagonalisable sur une base orthonormée de vecteurs propres.
Le sous espace propre associé à ![]() est de dimension
est de dimension ![]() (th du rang en dimension finie).
(th du rang en dimension finie).
En réordonnant les vecteurs de la base pour placer ceux associés à la valeur propre ![]() à la fin, on obtient donc une base orthonormée dans laquelle la matrice de
à la fin, on obtient donc une base orthonormée dans laquelle la matrice de ![]() est
est
![]() avec
avec ![]() diagonale à termes strictement positifs (les autres valeurs propres)
diagonale à termes strictement positifs (les autres valeurs propres)
6/ f/ Comme ![]() les
les ![]() derniers vecteurs de
derniers vecteurs de ![]() forment une base de
forment une base de ![]() et leurs images sont nulles.
et leurs images sont nulles.
Donc la matrice de ![]() dans la base
dans la base ![]() est de la forme
est de la forme ![]() où
où ![]()
Comme :
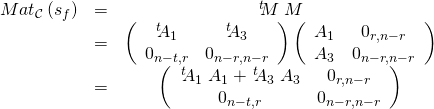
alors ![]()
![]()
7/ a/ Comme ![]() en substituant
en substituant ![]() à
à ![]() et
et ![]() à
à ![]()
On obtient que ![]() est l’endomorphisme associé à
est l’endomorphisme associé à ![]()
Donc ![]() et
et ![]()
![]()
donc d’après le théorème du rang en dimension finie
![]()
=![]()
=![]()
=![]()
Donc ![]()
et d’après le théorème du rang
![]()
7/ b/ Soit ![]() une valeur propre strictement positive de
une valeur propre strictement positive de ![]() et
et ![]() un vecteur propre associé, avec
un vecteur propre associé, avec ![]() colonne des coordonnées dans la base
colonne des coordonnées dans la base ![]()
On a ![]() donc
donc ![]()
Et comme ![]() et
et ![]() alors
alors ![]() et
et ![]() est vecteur propre de
est vecteur propre de ![]() associé à
associé à ![]() donc
donc ![]() est vecteur propre de
est vecteur propre de ![]() associé à
associé à ![]()
Donc ![]() et
et ![]()
Or ![]() restreinte à
restreinte à ![]() est injective :
est injective :
Soit ![]() tel que
tel que ![]()
alors ![]() donc
donc ![]() et
et
comme ![]()
![]() et
et ![]()
Donc ![]() bijective de
bijective de ![]() dans
dans ![]() et
et ![]() d’où
d’où
![]()
7/ c/ Comme ![]()
![]() est symétrique donc diagonalisable sur une base orthonormée de vecteurs propres.
est symétrique donc diagonalisable sur une base orthonormée de vecteurs propres.
Par égalité des dimension des noyaux, ![]() valeur propre de
valeur propre de ![]()
![]() valeur propre de
valeur propre de ![]()
Si ![]() valeur propre non nulle de
valeur propre non nulle de ![]() alors
alors ![]() valeur propre de
valeur propre de ![]()
Et réciproquement en substituant ![]() à
à ![]() donc
donc ![]() et
et ![]() ont les mêmes valeurs propres nulles ou pas
ont les mêmes valeurs propres nulles ou pas
Et ![]() ,
, ![]()
donc, pour ![]() et
et ![]()
7/ d/ ![]() et
et ![]() ont des valeurs propres (nulles ou pas) identiques et des sous espaces propres de même dimension.
ont des valeurs propres (nulles ou pas) identiques et des sous espaces propres de même dimension.
Donc, en réordonnant pour chacun les vecteurs d’une base orthonormée de vecteurs propres par ordre décroissant (pour avoir les ![]() à la fin )
à la fin )
Il existe deux bases ![]() et
et ![]() orthonormées telles que
orthonormées telles que ![]()
On a donc ![]() et
et ![]()
et ![]()
=![]()
=![]()
donc, avec ![]() qui est orthogonale (produit de matrices orthogonales)
qui est orthogonale (produit de matrices orthogonales)
![]()
8/ a/ La fonction ![]() est continue (polynôme) sur
est continue (polynôme) sur ![]() donc
donc ![]() image réciproque d’un fermé, est un fermé de
image réciproque d’un fermé, est un fermé de ![]()
Pour tout ![]() (tous les
(tous les ![]() )
) ![]()
![]() donc, pour
donc, pour ![]()
![]() et
et ![]()
Donc ![]() partie fermée bornée de
partie fermée bornée de ![]() .
.
8/ b/ ![]() est continue (polynôme) sur un fermé bornée donc
est continue (polynôme) sur un fermé bornée donc ![]() admet un maximum global noté
admet un maximum global noté ![]() sur
sur ![]()
8/ c/ Lorsque ![]() au moins un des
au moins un des ![]() est nul donc
est nul donc ![]() pour
pour ![]() .
.
8/ d/ Comme ![]() n’est pas le maximum de
n’est pas le maximum de ![]() sur
sur ![]() le maximum est atteint sur
le maximum est atteint sur ![]()
Donc, ![]() est le maximum de
est le maximum de ![]() sur
sur ![]() donc sur
donc sur ![]() sous la contrainte
sous la contrainte ![]()
8/ e/ Soit ![]() et
et ![]() contrainte linéaire,
contrainte linéaire, ![]()
![]() (polynômiale) est
(polynômiale) est ![]() sur l’ouvert
sur l’ouvert ![]() et
et ![]()
Donc, si ![]() est un extremum de
est un extremum de ![]() sous la contrainte
sous la contrainte ![]() il existe
il existe ![]() tel que
tel que ![]()
Donc,pour tout ![]() et
et ![]() et comme
et comme ![]()
![]() donc
donc ![]() et
et ![]()
(tous les ![]() sont égaux)
sont égaux)
Comme ![]() on a alors
on a alors ![]() pour tout
pour tout ![]() .
.
Comme c’est la seule solution possible et que ![]() est une solution, alors
est une solution, alors ![]() et
et ![]() .
.
8/ f/ Comme ![]()
on a, avec ![]()
=![]()
et ![]() donc
donc ![]()
Donc la valeur en ![]() est inférieure ou égale au maximum :
est inférieure ou égale au maximum :
![]()
![]()
d’où ![]()
L’égalité est atteinte au seul maximum, ![]() donc si et seulement
donc si et seulement ![]() pour tout
pour tout ![]() .
.
On a alors les ![]() tous égaux. Et réciproquement, s’ils sont tous égaux,
tous égaux. Et réciproquement, s’ils sont tous égaux, ![]() pour tout
pour tout ![]()
Donc égalité ![]()
![]() est un multiple de
est un multiple de ![]() .
.
8/ g/ La matrice ![]() a pour liste étendue de valeurs propres
a pour liste étendue de valeurs propres ![]()
En partant de l’écriture diagonalisée :
![]() et
et ![]()
Ce qui donne la liste étendue des valeurs propres
Pour tout ![]()
![]() est symétrique à valeurs propres positives ou nulles.
est symétrique à valeurs propres positives ou nulles.
En effet, les ![]() le sont déjà donc les
le sont déjà donc les ![]() également.
également.
Donc
![]()
Avec
![]()
=![]()
=![]()
d’où
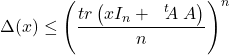
=![]()
Partie III. Etude de deux cas particuliers
9/ a/ La trace est invariante par changement de base car ![]() donc
donc
![]()
Pour un projecteur, ![]() et la juxtaposition de leurs bases est une base de
et la juxtaposition de leurs bases est une base de ![]() dans
dans
laquelle la matrice de ![]() est
est ![]()
![]() donc la trace de toute matrice représentant l’endomorphisme
donc la trace de toute matrice représentant l’endomorphisme ![]() est
est ![]()
9/ b/ Comme ![]() est un projecteur
est un projecteur ![]() et
et ![]()
Avec![]()
=![]()
donc ![]()
![]() donc
donc ![]()
Donc, ![]() est une matrice de projecteur d’ordre
est une matrice de projecteur d’ordre ![]() et de rang
et de rang ![]() Donc
Donc ![]()
En effet, le rang d’une projection est sa trace. Donc
![]()
et donc ![]() (supplémentaires dans
(supplémentaires dans ![]() )
)
et ![]() .
.
9/ c/ On a donc ![]()
=![]() semblable à
semblable à ![]()
![]()
=![]()
=![]()
matrices de ![]() dans la base
dans la base ![]()
D’après 6/ c/ ![]() matrice diagonale des valeurs propres non nulles de
matrice diagonale des valeurs propres non nulles de ![]()
Donc ![]() est diagonale.
est diagonale.
Les valeurs propres de ![]() sont positives ou nulles, donc celles de
sont positives ou nulles, donc celles de ![]() sont
sont ![]() .
.
Donc ![]() est une matrice diagonale dont tous les termes sont
est une matrice diagonale dont tous les termes sont ![]()
Donc les valeurs propres non nulles de ![]() sont supérieures ou égales à
sont supérieures ou égales à ![]() .
.
En partant de l’écriture diagonalisée, ![]() est la somme de
est la somme de ![]() termes
termes ![]() donc
donc ![]()
9/ d/ Si ![]() alors
alors ![]() donc
donc ![]() donc
donc ![]() et
et ![]() est une projection orthogonale de rang
est une projection orthogonale de rang ![]() (sur un sous espace de dimension
(sur un sous espace de dimension ![]() )
)
10/ a/ Comme ![]()
![]() donc
donc ![]() est inversible (et
est inversible (et ![]() ) donc
) donc ![]() est inversible donc (produit)
est inversible donc (produit) ![]() est inversible et
est inversible et ![]()
10/ b/ Si ![]() est une valeur propre de
est une valeur propre de ![]() (inversible alors
(inversible alors ![]() ) et que
) et que ![]() est un vecteur propre
est un vecteur propre
associé alors ![]() donc (produit par l’inverse)
donc (produit par l’inverse) ![]() et
et ![]() donc
donc ![]() est une valeur propre de
est une valeur propre de ![]() donc de
donc de ![]()
Or, ![]() et
et ![]() ont les mêmes valeurs propres.
ont les mêmes valeurs propres.
Donc ![]() est aussi une valeur propre de
est aussi une valeur propre de ![]()
On a obtenu que si ![]() était vecteur propre de
était vecteur propre de ![]() associé à
associé à ![]() alors
alors ![]() était vecteur propre de
était vecteur propre de ![]() associé à
associé à ![]()
On a la réciproque de la même façon. Donc, les sous espaces propres ![]() et
et ![]() sont égaux.
sont égaux.
Et comme ![]() on a finalement
on a finalement ![]()
10/ c/ Signe de la différence :
![]()
=![]()
donc, pour tout ![]() et
et ![]()
10/ d/ ![]() est à valeurs propres positives ou nulles donc pour tout
est à valeurs propres positives ou nulles donc pour tout
![]() et comment obtenir une quantité
et comment obtenir une quantité ![]() , il faudrait que
, il faudrait que ![]() ?
?
![]() valeur propre
valeur propre ![]()
![]() valeur propre, à chaque valeur propre
valeur propre, à chaque valeur propre ![]() correspond une valeur propre
correspond une valeur propre ![]()
Et dans le produit :
![]()
=![]()
Et réciproquement.
Donc une autre liste étendue des valeurs propres est ![]()
Ces deux listes sont donc des permutations l’une de l’autre (elles comprennent les mêmes éléments dans des ordres distincts)
![]()
et ![]()
=![]()
Donc (termes positifs) ![]()
10/ e/ ![]()
si et seulement si tous les termes
![]()
=![]() valent
valent ![]()
C’est à dire si ![]() ,
,
c’est à dire si et seulement si
![]() pour tout
pour tout ![]()
Donc ![]()
=![]()
Ce qui signifie que ![]() est un endomorphisme symétrique, Donc que ses sous espaces propres sont orthogonaux. (
est un endomorphisme symétrique, Donc que ses sous espaces propres sont orthogonaux. (![]()
![]()
Réciproquement, si ![]()
![]() ,la juxtaposition de bases orthonormée de chacun, sera une base orthonormée de
,la juxtaposition de bases orthonormée de chacun, sera une base orthonormée de ![]() .
.
Dans cette base orthonormée, la matrice de ![]() sera diagonale, donc symétrique, et, donc dans toute base orthonormée la matrice de
sera diagonale, donc symétrique, et, donc dans toute base orthonormée la matrice de ![]() sera symétrique.
sera symétrique.
Cette égalité correspond au cas où ![]() est une symétrie orthogonale.
est une symétrie orthogonale.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie IV. Décomposition polaire
11/ ![]() est inversible, donc,
est inversible, donc, ![]() est inversible et
est inversible et ![]() n’est pas valeur propre.
n’est pas valeur propre.
Donc, toutes les valeurs propres de ![]() , c’est à dire de
, c’est à dire de ![]() sont strictement positives.
sont strictement positives.
![]() étant symétrique, il existe une base base orthonormée de vecteurs propres
étant symétrique, il existe une base base orthonormée de vecteurs propres ![]() et
et ![]() réels strictement positifs
réels strictement positifs ![]() (une liste étendue des valeurs propres) tels que
(une liste étendue des valeurs propres) tels que
![]()
L’image d’une base définit un endomorphisme de ![]() donc
donc ![]() est bien défini.
est bien défini.
La matrice de ![]() dans la base orthonormée
dans la base orthonormée ![]() est diagonale donc symétrique.
est diagonale donc symétrique.
Les valeurs propres de ![]() sont les
sont les ![]()
Donc ![]()
Et, pour tout ![]()
![]() et
et ![]() sont deux endomorphismes de
sont deux endomorphismes de ![]() qui coïncident sur une base et
qui coïncident sur une base et ![]()
12/ Soit ![]() alors
alors ![]() et
et ![]() avec
avec ![]() donc
donc ![]() valeur propre de
valeur propre de ![]() et
et ![]()
Donc ![]()
Réciproquement, on passe par la somme des dimensions des sous espaces propres.
Mais ![]() et
et ![]() auront les mêmes carrés.
auront les mêmes carrés.
Comme les ![]() sont positifs, les
sont positifs, les ![]() pour
pour ![]() sont distincts.
sont distincts.
![]() est diagonalisable donc
est diagonalisable donc ![]()
et ![]() donc
donc ![]()
Les ![]() sont distincts, donc les sous espaces propres
sont distincts, donc les sous espaces propres ![]() pour
pour ![]() sont en somme directe et
sont en somme directe et
![]()
Finalement, ![]() et
et ![]()
Donc ![]() pour tout
pour tout ![]()
Donc ![]() pour tout
pour tout ![]()
Et comme ![]()
![]() n’a pas d’autres valeurs propres.
n’a pas d’autres valeurs propres.
Donc ![]() et
et ![]()
13/ On a l’existence par la question 11. de ![]() tel
tel ![]()
et d’après 12., ![]() et
et ![]() ont même vecteurs propres.
ont même vecteurs propres.
Donc dans toute base orthonormée de vecteurs propres de ![]() est une base de vecteurs propres de
est une base de vecteurs propres de ![]() et sa matrice
et sa matrice ![]() est donc diagonale.
est donc diagonale.
Unicité : Soit ![]() un tel endomorphisme de
un tel endomorphisme de ![]()
D’après 12. ses valeurs propres sont ![]() et ses sous espaces propres sont
et ses sous espaces propres sont ![]() pour tout
pour tout ![]()
Un endomorphisme est défini par sa restriction à une famille de sous espaces supplémentaires.
Les sous espaces propres étant supplémentaires, et ![]() sur
sur ![]() cela défini donc un unique
cela défini donc un unique ![]() .
.
D’où l’existence et l’unicité de ![]() tel que
tel que ![]()
14/ Une matrice ![]() appartenant à
appartenant à ![]() telle que
telle que ![]()
![]() est une matrice canoniquement associée à un endomorphisme
est une matrice canoniquement associée à un endomorphisme ![]() symétrique dont toutes les valeurs propres sont positives ou nulles et tel que
symétrique dont toutes les valeurs propres sont positives ou nulles et tel que ![]()
D’après, 13, cet endomorphisme existe et est unique.
Donc il existe une unique matrice ![]() appartenant à
appartenant à ![]() telle que
telle que ![]()
![]()
15/ C’est une matrice carrée. On teste si sa transposée est bien son inverse :
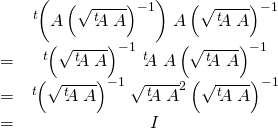
donc ![]() est orthogonale.
est orthogonale.
On a ![]() et
et ![]() orthogonale et
orthogonale et ![]() donc
donc ![]() et l’existence de la décomposition.
et l’existence de la décomposition.
Unicité : si ![]() tels que
tels que ![]() on voudrait que
on voudrait que ![]()
Or, ![]()
Or ![]() symétrique donc
symétrique donc ![]() car
car ![]()
Et comme ![]() est l’unique matrice symétrique à valeurs propres positives donc le carré est
est l’unique matrice symétrique à valeurs propres positives donc le carré est ![]() alors
alors ![]() d’où la valeur de
d’où la valeur de ![]()
Il y a donc un unique couple ![]() tel que
tel que ![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie V. Application à la distance d’une matrice
inversible à l’ensemble 
16/ ![]() est un ensemble non vide et minoré par
est un ensemble non vide et minoré par ![]()
Donc il a une borne inférieure.
Donc ![]() est bien définie.
est bien définie.
17/ ![]()
=![]()
=![]()
car ![]()
![]()
=![]()
=![]()
=![]()
car
![]()
=![]()
pour toutes matrices ![]() et
et ![]()
Donc, ![]()
![]() .
.
![]() est une application de
est une application de ![]() dans
dans ![]()
Soit ![]() alors
alors ![]() et
et ![]()
Et elle a pour réciproque ![]() donc elle est bijective de
donc elle est bijective de ![]() dans
dans ![]()
de même pour ![]()
![]() est plus petite que toutes les distances.
est plus petite que toutes les distances.
et ![]()
avec ![]()
donc ![]()
Donc ![]() est un minorant de
est un minorant de ![]() pour tout
pour tout ![]()
Donc, le plus grand des minorants, ![]() est plus grand :
est plus grand :
![]() donc
donc ![]()
Et de même ![]()
donc ![]()
et ![]()
et ![]()
Et de même pour l’autre coté avec ![]()
donc ![]()
18/ On a, d’après 17, ![]()
=![]() car
car ![]()
![]() car
car ![]()
Donc ![]()
19/ a/ ![]() est symétrique réelle donc diagonalisable.
est symétrique réelle donc diagonalisable.
19/ b/ Avec ![]() la colonne des coordonnées de
la colonne des coordonnées de ![]()
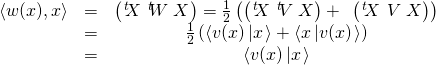
et ![]() donc
donc ![]()
=![]() et que
et que
![]()
![]() (Cauchy-Schwarz)
(Cauchy-Schwarz)
donc ![]() et la différence
et la différence
![]()
=![]() .
.
19/ c/ Soit ![]() valeur propre de
valeur propre de ![]() et
et ![]() une colonne propre associée
une colonne propre associée
![]()
et ![]()
=![]()
=![]()
Et comme ![]()
![]() les valeurs propres de
les valeurs propres de ![]() sont positives ou nulles.
sont positives ou nulles.
19/ d/ ![]()
=![]()
et ![]()
=![]()
19/ e/ Si ![]() alors, pour tout
alors, pour tout ![]()
![]()
Si pour tout ![]()
![]() il faut montrer que
il faut montrer que ![]()
On a alors ![]() qui est aussi la somme des valeurs propres étendues.
qui est aussi la somme des valeurs propres étendues.
Comme elles sont toutes positives ou nulle, elles sont toutes nulles.
Donc (matrice diagonalisable) ![]() et
et ![]()
![]() pour tout
pour tout ![]() si, et seulement si,
si, et seulement si,![]()
20/ a/ Identité remarquable ![]() ici :
ici :
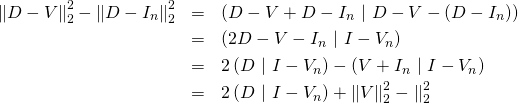
et comme
=![]()
=![]()
Donc
![]()
et comme ![]() est diagonale,
est diagonale,
![]()
=![]()
=![]()
=![]()
=![]()
Donc ![]()
=![]() et
et ![]()
=![]() .
.
20/ b/ ![]()
avec ![]()
Comme ![]() est diagonale à termes positifs , les termes de la diagonale de
est diagonale à termes positifs , les termes de la diagonale de
![]()
sont les ![]()
Donc
![]()
donc ![]() .
.
20/ c/ On a vu que ![]()
Et, pour tout ![]()
![]()
et ![]() est un minorant des
est un minorant des ![]()
pour ![]()
donc ![]()
Et, avec ![]()
On a aussi ![]()
Donc ![]()
=![]()
=![]()
Et comme ![]() avec
avec ![]() orthogonale,
orthogonale,
![]()
=![]()
et ![]()
=![]()
Et si ![]()
=![]()
alors ![]()
donc ![]() , somme de termes positifs ou nuls, est nulle.
, somme de termes positifs ou nuls, est nulle.
Donc tous les termes diagonaux sont nuls.
Donc , pour tout ![]()
![]() et comme les
et comme les ![]() sont strictement positifs, non nuls,
sont strictement positifs, non nuls, ![]()
D’où 19.e) :
![]() et
et ![]()
=![]()
On a alors ![]()
=![]() et
et ![]()
=![]()
et ![]()
Donc (polynôme annulateur) ![]() est la seule valeur propre de
est la seule valeur propre de ![]() et comme
et comme ![]() est diagonalisable,
est diagonalisable, ![]()
Donc ![]() est l’unique élément
est l’unique élément ![]() de
de
![]() tel que
tel que ![]()

