Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Mon parcours pour réussir en ECS2
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,8 sur 5
Corrigé du sujet HEC Maths 2 ECS 2019
Revenir à tous les corrigés des annales maths BCE
Partie I. Fonction logistique et lois logistiques
1/ a/ Pour tout ![]() , on a
, on a ![]() . La fonction
. La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() en tant qu’inverse de fonction de classe
en tant qu’inverse de fonction de classe ![]() sur
sur ![]() qui ne s’annule pas. De plus,
qui ne s’annule pas. De plus,
![]()
donc ![]() est strictement croissante sur
est strictement croissante sur ![]() . Enfin, les limites ne posent pas de problème, on a
. Enfin, les limites ne posent pas de problème, on a
![]()
On en déduit que ![]() est continue et strictement croissante donc réalise une bijection de
est continue et strictement croissante donc réalise une bijection de ![]() dans
dans ![]() .
.
Déterminons sa bijection réciproque : soit ![]() et
et ![]() tels que
tels que
![]() = y
= y
![]()
![]()
![]()
![]()
1/ b/ D’après le calcul précédent :
![]()
1/ c/ On pose la fonction ![]() définie sur
définie sur ![]() par
par ![]() .
. ![]() est dérivable en tant que somme de telles fonctions et
est dérivable en tant que somme de telles fonctions et
![]()
de plus
![]()
donc, comme ![]() est continue et strictement décroissante sur
est continue et strictement décroissante sur ![]() , elle réalise une bijection de
, elle réalise une bijection de ![]() dans
dans ![]() donc en particulier, il existe un unique
donc en particulier, il existe un unique ![]() , tel que
, tel que ![]() , i.e.
, i.e. ![]() .
.
1/ d/ Avec les notations précédentes, l’inégalité demandée est en fait
![]()
Or ![]() est de classe
est de classe ![]() sur
sur ![]() et sa dérivée vérifie
et sa dérivée vérifie
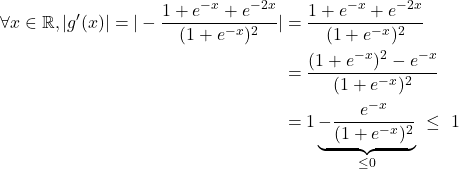
donc par l’inégalité des accroissements finis, on a bien
![]()
2/ a/ On rappelle la notation ![]() .
.
On utilise l’algorithme de dichotomie avec la fonction ![]() pour estimer la valeur de
pour estimer la valeur de ![]() tel que
tel que ![]() .
.
Comme ![]() est décroissante et que
est décroissante et que ![]() et
et ![]() , on sait, par le théorème de la bijection, que
, on sait, par le théorème de la bijection, que ![]() s’annule sur
s’annule sur ![]() donc on peut restreindre l’étude de
donc on peut restreindre l’étude de ![]() sur
sur ![]() pour trouver une valeur approchée de
pour trouver une valeur approchée de ![]() : cela justifie les choix de
: cela justifie les choix de ![]() et
et ![]() .
.
La condition ![]() revient donc à
revient donc à ![]() donc comme
donc comme ![]() est décroissante, la condition
est décroissante, la condition ![]() signifie que la fonction s’annule sur
signifie que la fonction s’annule sur ![]() , sinon, la fonction s’annule sur
, sinon, la fonction s’annule sur ![]() . On propose donc
. On propose donc
Lambda(c)>c then a=c ; else b=c; end;
2/ b/ À la fin de la boucle while, on sait que l’on aura ![]() , donc
, donc
![]()
c’est-à-dire que tout élément de l’intervalle ![]() est distant du milieu de l’intervalle,
est distant du milieu de l’intervalle, ![]() , d’au plus
, d’au plus ![]() . Ainsi,
. Ainsi, ![]() est une approximation de
est une approximation de ![]() à
à ![]() près.
près.
La valeur maximale que l’on peut affectée en ligne (4) est donc ![]() .
.
2/ c/ Le ![]() renvoyé par Scilab n’est pas le vrai
renvoyé par Scilab n’est pas le vrai ![]() , mais n’est qu’une valeur approchée. D’après l’inégalité 1.d), on peut dire que la valeur numérique renvoyée par l’instruction (10) est un nombre compris entre
, mais n’est qu’une valeur approchée. D’après l’inégalité 1.d), on peut dire que la valeur numérique renvoyée par l’instruction (10) est un nombre compris entre ![]() et
et ![]() , a priori plus petite en valeur absolue que l’erreur commise.
, a priori plus petite en valeur absolue que l’erreur commise.
3/ a/ On a vu en question 1.a) que ![]() est une fonction de répartition d’une variable à densité. De plus, comme
est une fonction de répartition d’une variable à densité. De plus, comme ![]() est de classe
est de classe ![]() sur tout
sur tout ![]() , sa dérivée
, sa dérivée ![]() est bien une densité.
est bien une densité.
3/ b/ On rappelle que
![]()
donc
![]()
la fonction est donc paire.
La fonction ![]() est de classe
est de classe ![]() en tant que rapport de telles fonctions et
en tant que rapport de telles fonctions et
![]()
et
![]()
On voit que ![]() ne s’annule qu’en
ne s’annule qu’en ![]() . De plus,
. De plus, ![]() est positive sur
est positive sur ![]() et négative sur
et négative sur ![]() donc
donc ![]() est croissante sur
est croissante sur ![]() et décroissante sur
et décroissante sur ![]() et sa courbe représentative présente une tangente horizontale en
et sa courbe représentative présente une tangente horizontale en ![]() .
.
Déterminons les points d’inflexion : le signe de ![]() dépend uniquement de
dépend uniquement de ![]() . On effectue le tableau de signes suivant :
. On effectue le tableau de signes suivant :
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|ccccccc|}\hline$x$ & $-\infty$ & & $\ln(2-\sqrt 3)$&&$\ln(2+\sqrt 3)$&&$+\infty$ \\ \hline$e^x - 2 + \sqrt 3$ & &$-$ & $0$ & $+$ &$+$&$+$& \\\hline$e^x - 2 - \sqrt 3$ & &$-$ & $-$ & $-$ &$0$&$+$& \\\hline$\lambda''(x)$ & & $+$ & $0$ & $-$ & $0$ & $+$ & \\\hline\end{tabular}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-045e673efbb1994a6b8341a9ae44600a_l3.png)
On en déduit que la courbe représentative de ![]() présente deux points d’inflexions en
présente deux points d’inflexions en ![]() et
et ![]() . De plus,
. De plus, ![]() est convexe sur
est convexe sur ![]() et
et ![]() et concave sur
et concave sur ![]() .
.
Remarque : On a
![]()
donc ![]() . Cela confirme que la fonction
. Cela confirme que la fonction ![]() est paire et que les points d’inflexion sont bien symétriques l’un par rapport à l’autre par la droite des ordonnées.
est paire et que les points d’inflexion sont bien symétriques l’un par rapport à l’autre par la droite des ordonnées.
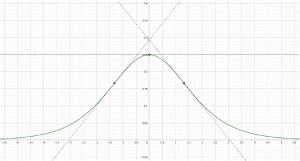
On a représenté ici (grâce à Geogebra) la courbe représentative de la fonction dans un repère orthogonal (mais non orthonormé), en représentant aussi les tangentes au points d’abscisses ![]() (ce sont les points d’inflexion, on constate que les tangentes « traversent » bien la courbe en ces points) et
(ce sont les points d’inflexion, on constate que les tangentes « traversent » bien la courbe en ces points) et ![]() (tangente horizontale). On rappelle que
(tangente horizontale). On rappelle que ![]() .
.
4/ a/ Soit ![]() une variable aléatoire suivant la loi logistique standard. Montrons que
une variable aléatoire suivant la loi logistique standard. Montrons que ![]() admet des moments à tout ordre. Soit
admet des moments à tout ordre. Soit ![]() ,
, ![]() admet un moment d’ordre
admet un moment d’ordre ![]() si et seulement si
si et seulement si
![]()
converge absolument. La fonction ![]() est continue et positive sur
est continue et positive sur ![]() et comme elle est paire sur
et comme elle est paire sur ![]() , on sait que
, on sait que
![]()
or, par croissance comparée, au voisinage de ![]()
![]()
donc ![]() donc par comparaison d’intégrales de fonctions positives, on en déduit que l’intégrale
donc par comparaison d’intégrales de fonctions positives, on en déduit que l’intégrale
![]()
converge, donc par parité, l’intégrale
![]()
converge absolument. On en déduit que ![]() admet un moment d’ordre
admet un moment d’ordre ![]() , pour tout
, pour tout ![]() .
.
Si ![]() , alors
, alors ![]() suit une loi logistique standard et donc admet un moment d’ordre
suit une loi logistique standard et donc admet un moment d’ordre ![]() , pour tout
, pour tout ![]() , donc
, donc
![Rendered by QuickLaTeX.com \[Y^k \ = \ (sZ+r)^k \ = \ \sum_{j=0}^k \binom{k}j s^j Z^j r^{k-j}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1bfc30dcd4117a41055ccfc77cb55d0c_l3.png)
admet une espérance comme combinaison linéaire de variables aléatoires admettant une espérance.
Calcul de l’espérance de ![]() :
:
![]()
On en déduit que ![]() . On en déduit alors que si
. On en déduit alors que si ![]() suit la loi logistique
suit la loi logistique ![]() donc
donc
![]()
4/ b/ On utilise la méthode d’inversion pour simuler la loi logistique standard. Si ![]() , alors montrons que
, alors montrons que ![]() suit la loi logistique standard. En effet, si on note
suit la loi logistique standard. En effet, si on note ![]() la fonction de répartition de
la fonction de répartition de ![]() , alors pour tout
, alors pour tout ![]()
![]()
On en déduit que ![]() suit bien une loi logistique standard. Ainsi, pour simuler une loi logistique
suit bien une loi logistique standard. Ainsi, pour simuler une loi logistique ![]() , on utilise le fait que si
, on utilise le fait que si ![]() suit une loi logistique standard, on a
suit une loi logistique standard, on a ![]() . On propose donc le programme suivant : on initialise une matrice au format adaptée puis on la remplit en utilisant deux boucles imbriquées :
. On propose donc le programme suivant : on initialise une matrice au format adaptée puis on la remplit en utilisant deux boucles imbriquées :
function S=grandlogis(n,p,r,s)
S = zeros(n,p)
for i=1:n
for j=1:p
U = rand() on simule une loi uniforme sur ]0,1[
Z = log(U/(1-U)) // L(U)
S(i,j) = s*Z + r
end
end
endfunction
4/ c/ Soit ![]() . Tout d’abord, par la formule de Koenig-Huygens, on a
. Tout d’abord, par la formule de Koenig-Huygens, on a
![]()
Si on dispose d’un ![]() -échantillon i.i.d. de même loi que
-échantillon i.i.d. de même loi que ![]() (de loi logistique
(de loi logistique ![]() ),
), ![]() , alors
, alors ![]() est un
est un ![]() -échantillon i.i.d. admettant un moment d’ordre
-échantillon i.i.d. admettant un moment d’ordre ![]() (car
(car ![]() admet un moment d’ordre
admet un moment d’ordre ![]() ), donc par la loi faible des grands nombres
), donc par la loi faible des grands nombres
![Rendered by QuickLaTeX.com \[\frac 1 n \sum_{k=1}^n Y_k^2 \ \underset{n\to +\infty}{\longrightarrow} \ \mathbb{E}(Y^2) \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-aae97b8437b145ab0f8f801cbd51a1d9_l3.png)
Ainsi, on propre le script suivant pour calculer une valeur approchée de ![]() et (donc de
et (donc de ![]() en retranchant
en retranchant ![]() ) en utilisant la loi faible des grands nombres (méthode de Monte-Carlo)
) en utilisant la loi faible des grands nombres (méthode de Monte-Carlo)
r = input() on laisse l’utilisateur choisir les paramètres
s = input()
n = 10000 n suffisamment grand
Y = grandlogis(n,1,r,s)
S = 0
for i=1:n
S = S + Y(i)^2
end
S = S/n – r^2
disp(S)
Remarque : Les lignes 5 à 9 du programme précédent peuvent être remplacées par : S = mean(Y.^2) – r^2
5/ a/ On écrit
![]()
On commence par déterminer une densité de ![]() et de
et de ![]() .
.
Soit ![]() la fonction de répartition de
la fonction de répartition de ![]() et
et ![]() celle de
celle de ![]() : soit
: soit ![]()
![]()
On en déduit que ![]() et
et ![]() sont bien des variables à densités (car
sont bien des variables à densités (car ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() ) et admettent respectivement comme densité
) et admettent respectivement comme densité
![]()
Montrons que le produit convolution ![]() est bien défini. On a
est bien défini. On a ![]() continue sur
continue sur ![]() et
et
![]()
donc ![]() est bornée. On en déduit que
est bornée. On en déduit que ![]() existe bien et définit une densité de probabilité.
existe bien et définit une densité de probabilité.
Comme ![]() et
et ![]() sont indépendantes (car
sont indépendantes (car ![]() et
et ![]() sont indépendantes), alors
sont indépendantes), alors ![]() est une variable à densité admettant
est une variable à densité admettant ![]() comme densité.
comme densité.
Calculons maintenant ![]() : soit
: soit ![]()
![]()
= ![]()
= ![]()
= ![]()
On effectue alors le changement de variable ![]() (ce changement de variable est valide car
(ce changement de variable est valide car ![]() est de classe
est de classe ![]() et strictement croissante sur
et strictement croissante sur ![]() ),
),
![]()
= ![]()
= ![]()
= ![]()
(![]() )
)
= 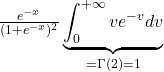
= ![]()
On en déduit que ![]() admet
admet ![]() pour densité donc
pour densité donc ![]() suit bien une loi logistique standard.
suit bien une loi logistique standard.
5/ b/ On en déduit le programme suivant permettant de simuler une variable aléatoire suivant la loi logistique standard
U = grand(1,2,’exp’,1) (on simule U1 et U2)
Z = log(U(1)/U(2))
disp(Z)
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie II. Variance de la loi logistique standard
6/ a/ On a ![]() et
et ![]() .
.
6/ b/ Soit ![]() . Pour tout
. Pour tout ![]() , on a
, on a ![]() et
et ![]() donc
donc ![]() . De plus, son coefficient dominant est
. De plus, son coefficient dominant est
![]()
Pour le coefficient du monôme en ![]() , on écrit d’une part
, on écrit d’une part
![Rendered by QuickLaTeX.com \[(X-1)^n = \sum_{j=0}^n \binom{n}j (-1)^j X^{n-j} \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-44914ca85ff54bd7006ba62ced209e95_l3.png)
donc la contribution de ![]() pour le monôme
pour le monôme ![]() est
est
![]()
On en déduit que le coefficient devant ![]() pour
pour ![]() vaut
vaut
![]()
6/ c/ On sait que ![]() est de degré
est de degré ![]() et on connait son coefficient dominant, donc en posant
et on connait son coefficient dominant, donc en posant ![]() ses racines (non nécessairement deux à deux distinctes), on peut écrire
ses racines (non nécessairement deux à deux distinctes), on peut écrire
![Rendered by QuickLaTeX.com \[P_n = (2n+1) \prod_{k=1}^n (X-z_k)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-01ac926b50f941ce8c25818cee9f3116_l3.png)
Si on développe cette expression, on s’aperçoit que le coefficient devant le monôme ![]() vaut
vaut
![Rendered by QuickLaTeX.com \[-(2n+1)\sum_{k=1}^n z_k \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2d850b57b0d3665faece51946a92e4cc_l3.png)
En effet, en développant, les termes facteurs de ![]() sont ceux pour lesquels on a choisi
sont ceux pour lesquels on a choisi ![]() fois
fois ![]() et une fois l’un des
et une fois l’un des ![]() et il y en a
et il y en a ![]() que l’on somme.
que l’on somme.
On identifie alors les coefficients devant le monôme ![]() et on obtient
et on obtient
![Rendered by QuickLaTeX.com \[-(2n+1)\sum_{k=1}^n z_k \ = \ - \frac{2}3 n(n+1)(2n+1) \ \Rightarrow \ \sum_{k=1}^n z_k \ = \ \frac{2}3 n(n+1)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-dc74558712a0d1c286cbb38bd7b1d709_l3.png)
7/ a/ Tout d’abord
![]()
donc on a bien
![]()
Ensuite, par le binôme de Newton, on écrit
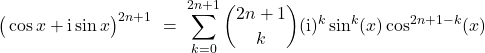
Or, on sait que (par une récurrence élémentaire par exemple)
![Rendered by QuickLaTeX.com \[(\operatorname{i})^k \ = \ \begin{cases}1 & \SI \exists j \in \Z, \ k = 4j \\\operatorname{i} & \SI \exists j \in \Z, \ k = 4j+1 \\-1 & \SI \exists j \in \Z, \ k = 4j+2 \\-\operatorname{i} & \SI \exists j \in \Z, \ k = 4j+3 \\\end{cases}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-39da789a69016890e9740cfea603af3f_l3.png)
donc si on prend la partie imaginaire de la somme, seuls les indices impairs restent. On obtient
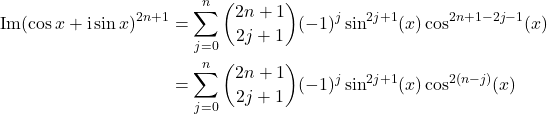
7/ b/ Soit ![]() (ce qui assure que
(ce qui assure que ![]() ), on a
), on a
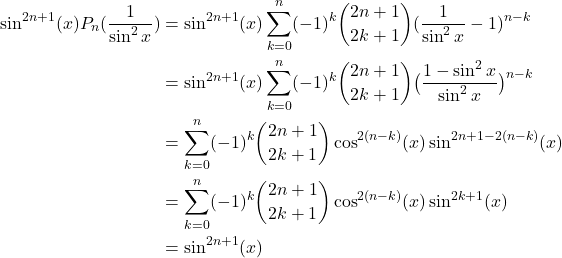
On peut donc conclure.
7/ c/ On remarque alors que pour tout ![]() , si on pose
, si on pose ![]() , on a
, on a
![]()
Or la fonction ![]() est strictement décroissante sur
est strictement décroissante sur ![]() (en effet, sa dérivée
(en effet, sa dérivée ![]() ) donc injective ce qui permet de dire si on pose pour tout
) donc injective ce qui permet de dire si on pose pour tout ![]() ,
, ![]() , que les
, que les ![]() sont deux à deux distincts. Ainsi, on a trouvé les
sont deux à deux distincts. Ainsi, on a trouvé les ![]() racines du polynôme
racines du polynôme ![]() , donc
, donc
![Rendered by QuickLaTeX.com \[\sum_{k=1}^n z_k = \frac{2}3 n(n+1) \Rightarrow \sum_{k=1}^n \frac 1 {\sin^2(k\pi/(2n+1))} = \frac{2}3 n(2n+1)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7e7591462df1534b2178c8eb89a667b0_l3.png)
8/ a/ On peut étudier les fonctions ![]() et
et ![]() sur
sur ![]() ou bien on peut remarquer que la fonction
ou bien on peut remarquer que la fonction ![]() est concave sur
est concave sur ![]() et la fonction
et la fonction ![]() est convexe (en effet, la dérivée seconde de
est convexe (en effet, la dérivée seconde de ![]() est la fonction
est la fonction ![]() qui est négative sur
qui est négative sur ![]() et la dérivée seconde de
et la dérivée seconde de ![]() est
est ![]() qui est positive sur
qui est positive sur ![]() ) de plus, la droite d’équation
) de plus, la droite d’équation
![]()
est la tangente en ![]() à la fois pour la courbe de la fonction sinus et de la fonction tangente donc par propriété de la convexité
à la fois pour la courbe de la fonction sinus et de la fonction tangente donc par propriété de la convexité
![]()
Ensuite, comme ![]() sur
sur ![]() , on peut écrire
, on peut écrire
![]()
ce qui est l’inégalité demandée.
8/ b/ On remarque que pour tout ![]() , on a
, on a
![Rendered by QuickLaTeX.com \[0 < \frac{k \pi}{2n+1} \leq \underbrace{\frac{n}{2n+1}}_{< 1/2} \pi < \frac{\pi}2\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-58b3c458e76e088fbea1c30bb0e9348b_l3.png)
En utilisant l’inégalité précédente, on obtient donc
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^n \frac 1 {\sin^2(k\pi/(2n+1))} \leq \sum_{k=1}^n ( \frac 1 {(k\pi/(2n+1))^2} + 1) = \frac{(2n+1)^2}{\pi^2} \sum_{k=1}^n \frac 1 {k^2} + n\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-96c518d9bd7284da6a6b229d3e594053_l3.png)
on a donc d’une part
![Rendered by QuickLaTeX.com \[\frac{(2n+1)^2}{\pi^2}\sum_{k=1}^n \frac 1 {k^2} \geq \sum_{k=1}^n \frac 1 {\sin^2(k\pi/(2n+1))} - n = \frac{2}3 n^2 - \frac 1 3 n = \frac{1}3 n(2n-1)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-97e8a8cb960f5c3c29705f5eb70afe21_l3.png)
et d’autre part, par l’inégalité précédente
![Rendered by QuickLaTeX.com \[ \frac{2}3 n(n+1) = \sum_{k=1}^n \frac 1 {\sin^2(k\pi/(2n+1))} \geq \sum_{k=1}^n \frac 1 {(k\pi/(2n+1))^2} = \frac{(2n+1)^2}{\pi^2} \sum_{k=1}^n \frac 1 {k^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-dc66599fab13702a31aa3a38dea1a25b_l3.png)
On obtient donc
![Rendered by QuickLaTeX.com \[\frac 1 3 n (2n-1) \leq \frac{(2n+1)^2}{\pi^2} \sum_{k=1}^n \frac 1 {k^2} \leq \frac{2}3 n(n+1)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-67e439de7692af31b73c99d5098fe728_l3.png)
8/ c/ On a donc, pour tout ![]()
![Rendered by QuickLaTeX.com \[\frac{\pi^2}{3} \frac{n(2n-1)}{(2n+1)^2} \leq \sum_{k=1}^n \frac 1 {k^2} \leq \frac{2\pi^2}3 \frac{n(n+1)}{(2n+1)^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a0a5321f5942f8a6bc933cefa18fc0f5_l3.png)
or
![]()
donc par encadrement, on en déduit que
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{+\infty} \frac 1 {k^2} = \limn \sum_{k=1}^n \frac 1 {k^2} = \frac{\pi^2}6\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-01600b0b15fc79c2dee6c019a8cadd3b_l3.png)
9/ a/ On rappelle que ![]() donc par la formule de Koenig-Huygens
donc par la formule de Koenig-Huygens
![]()
Notamment, l’intégrale ![]() converge en
converge en ![]() .
.
Pour tout ![]() , on a par intégration par partie (la fonction
, on a par intégration par partie (la fonction ![]() est bien de classe
est bien de classe ![]() sur
sur ![]() et sa dérivée est
et sa dérivée est ![]() )
)
![]()
or, par croissance comparée
![]()
donc en passant à la limite lorsque ![]() , on obtient que non seulement que l’intégrale
, on obtient que non seulement que l’intégrale ![]() converge bien mais on a aussi
converge bien mais on a aussi
![Rendered by QuickLaTeX.com \[\int_0^{+\infty} \frac{xe^{-x}}{1+e^{-x}}dx = \frac 1 2 \int_0^{+\infty} \underbrace{x^2 \frac{e^{-x}}{(1+e^{-x})^2}}_{\text{fct paire}}dx = \frac 1 4 \int_{-\infty}^{+\infty} x^2 \frac{e^{-x}}{(1+e^{-x})^2} dx = \frac 1 4 V(X)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-77a4c67ada151cfb7a68317ea381e2e2_l3.png)
9/ b/ Soit ![]() et soit
et soit ![]() , on a par linéarité de l’espérance
, on a par linéarité de l’espérance
![Rendered by QuickLaTeX.com \begin{align*}\sum_{k=0}^n (-1)^k \int_0^A x e^{-(k+1)x}dx & = & \int_0^A xe^{-x} \big( \sum_{k=0}^n (-e^{-x})^k \big) dx \\(\forall x \in [0,A], \ -e^{-x} \neq 1), \quad & = & \int_0^A xe^{-x} \frac{1-(-e^{-x})^{n+1}}{1+e^{-x}} dx \\&=& \int_0^A \frac{xe^{-x}}{1+e^{-x}}dx + (-1)^{n+1} \int_0^A \frac{xe^{-(n+2)x}}{1+e^{-x}}dx\end{align*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-14a3778059ca50be0219975c2ec56dfe_l3.png)
On justifie maintenant que les intégrales présentes convergent en ![]() en précisant qu’au voisinage de
en précisant qu’au voisinage de ![]()
![]()
on conclut par le critère de comparaison d’intégrales de fonctions positives. On peut donc passer à la limite lorsque ![]() et on obtient exactement ce qui est attendu.
et on obtient exactement ce qui est attendu.
9/ c/ On a, pour tout ![]() ,
,
![]()
donc par croissance de l’intégrale
![]()
or, si on considère ![]() , alors
, alors
![]()
On en déduit que ![]() donc par encadrement, on obtient
donc par encadrement, on obtient
![]()
On en déduit que lorsqu’on passe à la limite quand ![]() dans l’égalité de 9.c), on obtient
dans l’égalité de 9.c), on obtient
![Rendered by QuickLaTeX.com \[\int_0^{+\infty} \frac{xe^{-x}}{1+e^{-x}}dx = \sum_{k=0}^{+\infty} (-1)^k \int_0^{+\infty} x e^{-(k+1)x}dx = \sum_{k=0}^{+\infty} (-1)^k \frac 1 {(k+1)^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-109d20a0ccd75e912e96dfbd394f26ff_l3.png)
On rappelle que l’intégrale ![]() se calcule en passant par l’espérance d’une variable aléatoire suivant la loi
se calcule en passant par l’espérance d’une variable aléatoire suivant la loi ![]() .
.
9/ d/ On sait que
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{+\infty} \frac 1 {n^2} \ = \ \frac{\pi^2}6\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c3b4ef063d629a0830e0e1ea5495be18_l3.png)
on souhaite déterminer la valeur de la somme suivante
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{+\infty} \frac{(-1)^{k}}{(k+1)^2} = \sum_{n=1}^{+\infty} \frac{(-1)^{n-1}}{n^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2c3f872c041e6e5259e54be704cdb5a2_l3.png)
Pour tout ![]() , on pose
, on pose
![Rendered by QuickLaTeX.com \[S_n \ = \ \sum_{k=1}^{2n} \frac{(-1)^{k-1}}{k^2} \text{ et } T_n \ = \ \sum_{k=1}^{2n} \frac{1}{k^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1c5c9bc6d73fe9f0620bb32ad8b58370_l3.png)
On sait donc que ![]() . De plus, on remarque que
. De plus, on remarque que
![Rendered by QuickLaTeX.com \[T_n-S_n = \sum_{k=1}^{2n} \underbrace{\frac{1 - (-1)^{k-1}}{k^2}}_{=0 \: si \: k \text{ impair}} = \sum_{j=1}^n \frac{1 - (-1)^{2j-1}}{(2j)^2} = \frac 1 2 \sum_{j=1}^n \frac 1 {j^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-75762976350ac8bc3afa33b805a7e9be_l3.png)
donc ![]() . On en déduit que
. On en déduit que
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{+\infty} \frac{(-1)^k}{(k+1)^2} = \limn S_n = \limn ( T_n - (T_n -S_n)) = \frac{\pi^2}{12}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-693a2e6c36fc37d2421eca515f2f8ff2_l3.png)
On en déduit que
![Rendered by QuickLaTeX.com \[V(Z) = 4 \int_0^{+\infty} \frac{x e^{-x}}{1+e^{-x}}dx = 4 \sum_{k=0}^{+\infty} \frac{(-1)^k}{(k+1)^2} = \frac{\pi^2}3\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-bb85e587948a4d1e0ae940a1802cbdb6_l3.png)
10/ a/ Les fonctions ![]() et
et ![]() sont continues et positives sur
sont continues et positives sur ![]() . De plus, en
. De plus, en ![]() , on a par croissance comparée
, on a par croissance comparée
![]()
donc ![]() et
et ![]() donc comme
donc comme ![]() converge (intégrale de Riemann avec
converge (intégrale de Riemann avec ![]() ), on en déduit par comparaison d’intégrale de fonctions positives que
), on en déduit par comparaison d’intégrale de fonctions positives que
![]()
convergent.
Enfin, en ![]() , on a par croissance comparée
, on a par croissance comparée
![]()
on en déduit que ![]() et
et ![]() donc comme
donc comme ![]() converge, par comparaison d’intégrales de fonctions positives,
converge, par comparaison d’intégrales de fonctions positives,
![]()
convergent.
On en déduit que ![]() converge (car converge absolument) et que
converge (car converge absolument) et que ![]() converge.
converge.
10/ b/ Si on considère ![]() , alors par théorème de transfert
, alors par théorème de transfert
![]()
et donc par la formule de Koenig Huygens : ![]() .
.
Or, par la question 5.a), on sait que si ![]() et
et ![]() sont deux variables indépendantes de loi exponentielle de paramètre
sont deux variables indépendantes de loi exponentielle de paramètre ![]() , alors
, alors
![]()
suit une loi logistique standard. Ainsi, par indépendance
![]()
Or ![]() donc
donc ![]() .
.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie III. Estimation à partir de données binaires
11/ Comme ![]() est continue, on en déduit que
est continue, on en déduit que ![]() est de classe
est de classe ![]() sur
sur ![]() et admet pour dérivée
et admet pour dérivée ![]() . Comme
. Comme ![]() est strictement positive, on en déduit que
est strictement positive, on en déduit que ![]() est strictement croissante. De plus, par propriété d’une fonction de répartition
est strictement croissante. De plus, par propriété d’une fonction de répartition
![]()
et comme ![]() est continue et strictement croissante, on en déduit qu’elle réalise une bijection de
est continue et strictement croissante, on en déduit qu’elle réalise une bijection de ![]() dans
dans ![]() .
.
12/ Les variables aléatoires ![]() sont mutuellement indépendantes, de même loi de Bernoulli qui admet une variance, donc par le théorème limite central, on sait que
sont mutuellement indépendantes, de même loi de Bernoulli qui admet une variance, donc par le théorème limite central, on sait que
![Rendered by QuickLaTeX.com \[\frac{\overline{Y_n} - \mathbb{E}(\overline{Y_n})}{\sqrt{V(\overline{Y_n})}} \ \underset{n\to \infty}{\longrightarrow} Z \text{ o\`u } Z \hookrightarrow \mathcal{N}(0,1)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f319b842c3974b485e7fbb83cf0c64bb_l3.png)
Or par linéarité de l’espérance ![]() et par indépendance
et par indépendance
![Rendered by QuickLaTeX.com \[ V(\overline{Y_n}) = \frac 1 {n^2} \sum_{k=1}^n V(Y_k) = \frac{F(\theta)(1-F(\theta))}{n}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-035e85e2a06fb390b1741e87028d5ec4_l3.png)
donc
![]()
donc ![]() converge en loi vers une variable aléatoire suivant une loi normale centrée de variance
converge en loi vers une variable aléatoire suivant une loi normale centrée de variance ![]() .
.
13/ a/ Les variables ![]() sont à valeurs dans
sont à valeurs dans ![]() donc
donc ![]() est à valeurs dans
est à valeurs dans ![]() donc
donc
![Rendered by QuickLaTeX.com \[P_\theta (E_n) = 1 - P_\theta(\overline{Y_n} = 0) - P_\theta(\overline{Y_n} = 1) = 1 - P_\theta(\sum_{k=1}^n Y_k =0) - P_\theta(\sum_{k=1}^n Y_k = n)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-45fe33b2096dc18516bc9da00118dffd_l3.png)
or par indépendance des ![]() , on sait que
, on sait que ![]() donc
donc
![]()
Comme ![]() est à valeurs dans
est à valeurs dans ![]() , on en déduit que
, on en déduit que ![]() et
et ![]() donc
donc
![]()
donc ![]()
13/ b/ i) On commence par remarquer que
![]()
Si ![]() , alors
, alors ![]() et donc
et donc ![]() par stricte croissance de
par stricte croissance de ![]() donc
donc
![]()
Montrons maintenant que pour tout ![]() ,
, ![]() . Tout d’abord, comme
. Tout d’abord, comme ![]() est une variable aléatoire (en tant que somme de variables aléatoires), on sait que
est une variable aléatoire (en tant que somme de variables aléatoires), on sait que ![]() et
et ![]() sont éléments de la tribu
sont éléments de la tribu ![]() . De plus
. De plus
![]()
(en notant ![]() le complémentaire de
le complémentaire de ![]() ). Or, si
). Or, si ![]() alors
alors ![]() et donc
et donc
![Rendered by QuickLaTeX.com \[[T_n \leq x] \cap \overline{E_n} = \begin{cases}\emptyset & \SI x <0 \\\overline{E_n} & \SI x \geq 0\end{cases}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2d1e22ffaaf2d88622cf0137f224f9c4_l3.png)
donc dans tous les cas ![]() . De plus, par la question précédente
. De plus, par la question précédente ![]() par propriété sur les tribus donc
par propriété sur les tribus donc ![]() est bien élément de
est bien élément de ![]() .
.
13/ b/ ii) D’une part
![]()
donc par croissance de ![]() , on a
, on a
![]()
d’autre part, par la formule des probabilités totales, on a
![Rendered by QuickLaTeX.com \begin{align*}P_\theta(T_n \leq x) = P_\theta ([T_n \leq x] \cap E_n) +P_\theta (\underbrace{[T_n \leq x] \cap \overline{E_n}}_{\subset \overline E_n}) &\leq P_\theta ([T_n \leq x] \cap E_n) +P_\theta(\overline E_n) \\ & \leq P_\theta ([T_n \leq x] \cap E_n) + 1 - P_\theta (E_n)\end{align*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b869efeed8c2e2df2aad2dda68011d8f_l3.png)
13/ c/ Soit ![]() . Par la loi faible des grands nombres (les
. Par la loi faible des grands nombres (les ![]() sont i.i.d. et admettent une variance), on sait que
sont i.i.d. et admettent une variance), on sait que
![]()
autrement dit, pour tout ![]()
![]()
![]() Si
Si ![]() : alors
: alors ![]() donc
donc ![]() et donc
et donc
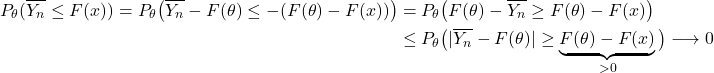
donc comme ![]() , on en déduit par encadrement que
, on en déduit par encadrement que ![]() . Comme
. Comme
![]()
on en déduit que ![]() .
.
![]() Si
Si ![]() , dans ce cas
, dans ce cas ![]() , alors
, alors
![]()
On en déduit que ![]() . Or par la formule du crible
. Or par la formule du crible
![]()
et comme ![]() et
et ![]() , on en déduit que
, on en déduit que ![]() et donc
et donc
![]()
De plus, ![]() , on en déduit par encadrement que
, on en déduit par encadrement que ![]() admet la même limite que
admet la même limite que ![]() donc
donc
![Rendered by QuickLaTeX.com \[\limn P_\theta (T_n \leq x) = \begin{cases}0 & \SI x < \theta \\1 & \SI x > \theta \end{cases}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3d33c84a2ecfb52fe54d1860bb8dc67b_l3.png)
13/ d/ Tout d’abord ![]() est bien une variable aléatoire qui ne dépend pas du paramètre inconnu
est bien une variable aléatoire qui ne dépend pas du paramètre inconnu ![]() : c’est donc bien un estimateur de
: c’est donc bien un estimateur de ![]() .
.
Ensuite, on écrit que pour tout ![]()
(1) ![]()
Comme ![]() , on en déduit que
, on en déduit que ![]() donc par la question précédente
donc par la question précédente
![]()
De plus, ![]() donc
donc
![]()
par la question précédente (![]() ) donc par encadrement
) donc par encadrement
![]()
et donc
![]()
On en déduit que la suite ![]() est une suite d’estimateurs convergente de
est une suite d’estimateurs convergente de ![]() .
.
Remarque : Le résultat précédent nous fait dire que ![]() mais ce n’est pas au programme de pouvoir conclure directement que cela implique la convergence en probabilité dans le cas d’une limite en loi déterministe.
mais ce n’est pas au programme de pouvoir conclure directement que cela implique la convergence en probabilité dans le cas d’une limite en loi déterministe.
14/ a/ i) La fonction ![]() est continue et strictement positive (donc ne s’annule pas). On en déduit que la fonction
est continue et strictement positive (donc ne s’annule pas). On en déduit que la fonction ![]() est continue sur
est continue sur ![]() . Ainsi, par définition de la continuité en
. Ainsi, par définition de la continuité en ![]() , on sait que pour tout
, on sait que pour tout ![]() (en particulier pour celui qu’on a fixé),
(en particulier pour celui qu’on a fixé),
![]()
ii) Si ![]() , alors
, alors ![]() donc si
donc si ![]()
![]()
On voit donc apparaître un taux d’accroissement de la fonction ![]() . Par le théorème des accroissements finis, on sait que pour tout
. Par le théorème des accroissements finis, on sait que pour tout ![]() avec
avec ![]() , il existe
, il existe ![]() tel que
tel que
![]()
Donc, en particulier, comme ![]() , on a par 14.a.i
, on a par 14.a.i
![]()
soit
![]()
De plus, on rappelle que ![]() , donc
, donc
![]()
14/ b/ On en déduit que pour tout ![]()
![]()
Or
![]()
avec
![]()
et
![]()
donc
![]()
On en déduit que
![]()
donc ![]() . (en probabilité)
. (en probabilité)
Remarque : Dans la définition de la convergence en probabilité, on regarde la limite de ![]() plutôt que
plutôt que ![]() . Cependant, en remarquant que
. Cependant, en remarquant que
![]()
on en déduit facilement que c’est en fait équivalent.
14/ c/ On écrit
![]()
or ![]() (en loi) où
(en loi) où ![]() et
et ![]() (en probabilité) donc par le théorème de Slutsky
(en probabilité) donc par le théorème de Slutsky
![]()
et donc ![]() converge en loi vers une variable aléatoire suivant une loi normale centrée et de variance
converge en loi vers une variable aléatoire suivant une loi normale centrée et de variance ![]() .
.
Partie IV. Régression logistique
15/ a/ Soit ![]() tel que
tel que ![]() . Alors
. Alors
![]()
par séparation de la norme. Or l’application ![]() est injective car la matrice
est injective car la matrice ![]() est de rang
est de rang ![]() (on rappelle que
(on rappelle que ![]() et
et ![]() ont même rang) et par le théorème du rang
ont même rang) et par le théorème du rang
![]()
On en déduit que ![]() et donc que
et donc que ![]() . On en déduit que
. On en déduit que ![]() est de rang
est de rang ![]() donc est inversible.
donc est inversible.
15/ b/ Soit ![]() . Pour cette question, on cherche à minimiser la quantité dépendant de
. Pour cette question, on cherche à minimiser la quantité dépendant de ![]() suivante
suivante
![]()
On pose ![]() . Par le théorème de projection orthogonale, on sait que la fonction
. Par le théorème de projection orthogonale, on sait que la fonction
![]()
admet un minimum global uniquement atteint pour ![]() , projeté orthogonal de
, projeté orthogonal de ![]() sur
sur ![]() .
.
Or, par injectivité de ![]() , on en déduit qu’il existe un unique vecteur
, on en déduit qu’il existe un unique vecteur ![]() tel que
tel que ![]() . Par propriété de la projection orthogonale, on sait que pour tout
. Par propriété de la projection orthogonale, on sait que pour tout ![]() , on a
, on a
![]()
En particulier, pour tout ![]() , comme
, comme ![]() , on a
, on a
![]()
En particulier, pour ![]() , on obtient
, on obtient
![]()
On a donc bien ce qui est demandé.
15/ c/ Supposons que l’on connaisse les lois des variables ![]() donc cela signifie que l’on connait la valeur de
donc cela signifie que l’on connait la valeur de ![]() et par bijectivité de la fonction
et par bijectivité de la fonction ![]() , cela signifie que l’on connait les valeurs de
, cela signifie que l’on connait les valeurs de ![]() , autrement dit, il existe
, autrement dit, il existe ![]() réels connus tel que
réels connus tel que
![Rendered by QuickLaTeX.com \[\begin{cases}<\alpha,{x^{(1)}}> & = \ \beta_1 \\<\alpha},{x^{(2)}}> & = \ \beta_2 \\\vdots \\<\alpha},{x^{(k)}}> & = \ \beta_k \\\end{cases} \Leftrightarrow ^{t}\hspace{-0.1cm}M A = B \text{ o\`u } B = \bpm \begin{pmatrix} \beta_1 \\ \vdots \\ \beta_k \end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5a0dc2ded092a4f75f69d531d245e38c_l3.png)
Dans le cas où ![]() n’est pas de rang
n’est pas de rang ![]() (donc
(donc ![]() n’est pas injective), l’équation matricielle
n’est pas injective), l’équation matricielle ![]() d’inconnue
d’inconnue ![]() admet potentiellement plusieurs solutions donc on ne peut pas déterminer
admet potentiellement plusieurs solutions donc on ne peut pas déterminer ![]() .
.
16/ a/ On rappelle que la fonction ![]() est la réciproque de la fonction de répartition
est la réciproque de la fonction de répartition ![]() . Ainsi, d’après la partie III, question 13, on sait que
. Ainsi, d’après la partie III, question 13, on sait que
![]()
(ici, les ![]() sont des variables de Bernoulli de paramètre
sont des variables de Bernoulli de paramètre ![]() donc c’est bien
donc c’est bien ![]() qui joue le rôle de
qui joue le rôle de ![]() ).
).
On en déduit que
![]()
Maintenant il faudrait utiliser un résultat hors programme pour justifier que la somme de suites de variables qui convergent en probabilités est une suite qui converge en probabilité. On démontre donc le lemme suivant :
Lemme : Soit ![]() et soit
et soit ![]() ,
, ![]() suites de variables aléatoires toutes définies sur un même espace probabilisé
suites de variables aléatoires toutes définies sur un même espace probabilisé ![]() tel qu’il existe
tel qu’il existe ![]() ,
, ![]() réels vérifiant :
réels vérifiant :
![]()
alors
![Rendered by QuickLaTeX.com \[\sum_{i=1}^k X_n^{(i)} \ \underset{n\to \infty}{\longrightarrow} \ \sum_{i=1}^k a_i\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3f050e519ece3c70227557a28f44e59f_l3.png)
Ce lemme permet de conclure que
![Rendered by QuickLaTeX.com \[\sum_{i=1}^k c_i T_{i,n} \ \underset{n\to \infty}{\longrightarrow} \ \sum_{i=1}^k c_i <\alpha},{x^{(i)}}>\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-93141f375f6f347dfff9f26db0328c48_l3.png)
Preuve du lemme :
On commence pour le cas de deux suites de variables : soit ![]() et
et ![]() tel que
tel que ![]() et
et ![]() .
.
Soit ![]() . Montrons que
. Montrons que
![]()
On commence par écrire que par inégalité triangulaire
![]()
donc, on a l’inclusion d’événements suivante
![]()
Ensuite, on remarque que
![]()
donc en passant au complémentaire et par De Morgan
![]()
On en déduit que
![]()
or
![Rendered by QuickLaTeX.com \begin{align*}P \Big(\big[ |X_n - a | \geq \epsilon /2 \big] \cup \big[ |Y_n - b| \geq \epsilon/2 \big]\Big) &= P(|X_n-a| \geq \epsilon/2) + P(|Y_n-b| \geq \epsilon/2) - \underbrace{P \Big(\big[ |X_n - a | \geq \epsilon /2 \big] \cap \big[ |Y_n - b| \geq \epsilon/2 \big]\Big)}_{\geq 0} \\ &\leq P(|X_n-a| \geq \epsilon/2) + P(|Y_n-b| \geq \epsilon/2) \\\end{align*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-df081fa3f94524e7e51a1ca75a1edac4_l3.png)
Finalement
![]()
par hypothèse ![]() et
et ![]() donc par encadrement, on en déduit que
donc par encadrement, on en déduit que
![]()
donc ![]() .
.
Dans le cas de plusieurs suites de variables aléatoires, on fait une récurrence sur ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*}HR_k &: Pour toutes suites de variables aléatoires \suites {X^{(1)}},..,\suites{ X^{(k)}} \text{ telles que } \\& \forall i \in [\![1,n]\!], \ \ X_n^{(i)} \underset{n\to \infty}{\longrightarrow} a_i \\&\text{on a } \quad \sum_{i=1}^k X^{(i)}_n \ \underset{n\to \infty}{\longrightarrow} \ \sum_{i=1}^k a_i\end{align*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ff0cb6335ad0468e572944ec35a77522_l3.png)
![]() La proposition est évidente dans le cas d’une suite de variables.
La proposition est évidente dans le cas d’une suite de variables.
![]() Soit
Soit ![]() tel que
tel que ![]() est vérifiée. Alors soit
est vérifiée. Alors soit ![]() suites de variables aléatoires telles que
suites de variables aléatoires telles que
![]()
alors par ![]() , si on pose
, si on pose ![]() , on a
, on a ![]() et comme
et comme ![]() , on a grâce au cas de deux suites
, on a grâce au cas de deux suites
![Rendered by QuickLaTeX.com \[Z_n + X_n^{(k+1)} \underset{n\to \infty}{\longrightarrow} \sum_{i=1}^k a_i + a_{k+1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7ef31576ae7c9b090c1429360b63fe2a_l3.png)
16/ b/ On note
![]()
Soit ![]() . Alors
. Alors
![Rendered by QuickLaTeX.com \[A_{i,n} = \sum_{j=1}^k c_{i,j} T_{j,n}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2920f25a498f8b60cac915d63e859a05_l3.png)
D’après la question précédente, on a
![Rendered by QuickLaTeX.com \[A_{i,n} \ \underset{n\to \infty}{\longrightarrow} \ A_i \ = \ \sum_{j=1}^k c_{i,j} <\alpha}{x^{(j)}}>\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-bb250129ff78ab13f294b76cc42270f0_l3.png)
On note 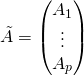 .
.
On rappelle que  donc
donc
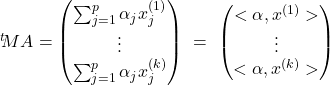 . On en déduit que
. On en déduit que
![]()
On peut donc conclure que
![]()

