Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EM Lyon Maths ECS 2019
Revenir à tous les corrigés des annales maths BCE
Partie A. Étude d’un endomorphisme de polynômes
1/ Pour tout polynôme ![]() de
de ![]() ,
, ![]() est une somme de polynômes donc c’est un polynôme, de plus
est une somme de polynômes donc c’est un polynôme, de plus ![]() donc
donc ![]() donc
donc ![]() en sommant on a :
en sommant on a : ![]() donc
donc ![]() .
.
Soit ![]() ,
, ![]()
![]()
Donc ![]() Donc
Donc ![]() est linéaire.
est linéaire.
Bilan : ![]() est un endomorphisme de
est un endomorphisme de ![]()
2/ On calcule ![]() et pour tout
et pour tout ![]() ,
,
![]()
Donc
![Rendered by QuickLaTeX.com \[\text{Mat}_{ {\cal B}}(\Psi_a)=\left( \begin{array}{ccccc}2& -a&0&\hdots & 0 \\0& 3 & -2a & 0& 0\\0& 0& 4 & \ddots & 0\\0 & \hdots & 0& \ddots& -na\\0 & \hdots & & 0& n+2\end{array} \right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4c3e893f2f6a33dfe1b755e191acc18d_l3.png)
3/ a/ ![]() est triangulaire donc les valeurs de sa diagonale sont ses valeurs propres c’est-à-dire :
est triangulaire donc les valeurs de sa diagonale sont ses valeurs propres c’est-à-dire : ![]() Il s’agit d’entiers consécutifs donc il y en a
Il s’agit d’entiers consécutifs donc il y en a ![]() or
or ![]() donc
donc ![]() est diagonalisable et son spectre est
est diagonalisable et son spectre est ![]()
Bilan : ![]() est diagonalisable et son spectre est
est diagonalisable et son spectre est ![]()
3/ b/ ![]() est un endomorphisme de
est un endomorphisme de ![]() et 0 n’est pas dans le spectre de
et 0 n’est pas dans le spectre de ![]() donc ce dernier est bijectif.
donc ce dernier est bijectif.
Bilan : ![]() est un automorphisme de
est un automorphisme de ![]()
3/ c/ On a ![]() Pour tout
Pour tout ![]() de
de ![]()
Bilan : Pour tout ![]() de
de ![]()
3/ d/ Pour tout ![]() de
de ![]() on voit que
on voit que ![]() n’est pas le polynôme nul donc
n’est pas le polynôme nul donc ![]() est vecteur propre de
est vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]()
Or le cardinal du spectre de ![]() est égal à la dimension de
est égal à la dimension de ![]() donc les sous-espaces propres de
donc les sous-espaces propres de ![]() sont tous de dimension 1 donc
sont tous de dimension 1 donc ![]() à lui seul forme une base de sous-espaces propres
à lui seul forme une base de sous-espaces propres ![]()
4/ a/ Pour tout polynôme ![]() de
de ![]() , on a
, on a
![]()
4/ b/ Pour tout polynôme ![]() de
de ![]() et pour tout réel
et pour tout réel ![]()
![]()
L’intégrale existe car on intègre une fonction continue sur un segment.
Or
![]()
Il reste le cas ![]() pour cela on voit que
pour cela on voit que ![]()
On a montré que les fonctions ![]() et
et ![]() coincident sur
coincident sur ![]() donc elles sont égales, en particulier
donc elles sont égales, en particulier ![]() est un polynôme de
est un polynôme de ![]()
Bilan : Pour tout polynôme ![]() de
de ![]() :
: ![]()
4/ c/ Soit ![]() est bien définie sur
est bien définie sur ![]() car les polynômes sont continues sur
car les polynômes sont continues sur ![]() donc on peut intégrer
donc on peut intégrer ![]() sur le segment
sur le segment ![]() pour tout réel
pour tout réel ![]()
De plus ![]() est bijective donc elle admet une fonction réciproque sur
est bijective donc elle admet une fonction réciproque sur ![]() Avec la question précédente, on peut écrire
Avec la question précédente, on peut écrire
![]()
Cela prouve que ![]() et
et ![]() coincident sur
coincident sur ![]() donc elles sont égales, en particulier cela prouve que
donc elles sont égales, en particulier cela prouve que ![]() est un endomorphisme bijectif de
est un endomorphisme bijectif de ![]() .
.
Bilan : ![]() est un automorphisme de
est un automorphisme de ![]() et
et ![]() donc
donc ![]()
4/ d/ Pour tout ![]() on a
on a ![]() , on peut diviser par
, on peut diviser par ![]() et
et ![]() donc
donc ![]()
Or ![]() est non nul et
est non nul et ![]() est bijective donc
est bijective donc ![]() est non nul donc
est non nul donc ![]() est vecteur propre de
est vecteur propre de ![]() associé à
associé à ![]()
La fonction ![]() est strictement décroissante sur
est strictement décroissante sur ![]() donc elle est injective donc
donc elle est injective donc ![]() est de cardinal
est de cardinal ![]() comme
comme ![]() donc
donc ![]() possède
possède ![]() valeurs propres sur
valeurs propres sur ![]() donc elle est diagonalisable.
donc elle est diagonalisable.
Bilan : ![]() est diagonalisable et son spectre est
est diagonalisable et son spectre est ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie B. Étude d’une fonction définie par une intégrale
5/ a/ On pose, pour tout ![]() de
de ![]() :
: ![]()
La fonction ![]() est continue sur
est continue sur ![]() donc par produit avec la fonction polynomiale
donc par produit avec la fonction polynomiale ![]() la fonction
la fonction ![]() est continue sur
est continue sur ![]() donc elle admet une primitive, notée
donc elle admet une primitive, notée ![]() sur
sur ![]() et
et
![]()
![]() est dérivable sur
est dérivable sur ![]() et sa dérivée est
et sa dérivée est ![]() Celle-ci est continue sur
Celle-ci est continue sur ![]() donc
donc ![]() est
est ![]() sur
sur ![]()
Donc ![]() est dérivable sur
est dérivable sur ![]() et, pour tout
et, pour tout ![]() de
de ![]()
![]()
Bilan : La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() et, pour tout
et, pour tout ![]() de
de ![]()
5/ b/ Soit ![]() Sur le segment
Sur le segment ![]()
![]() est continue donc elle admet un minimum atteint en un point noté
est continue donc elle admet un minimum atteint en un point noté ![]() et un maximum atteint en un point noté
et un maximum atteint en un point noté ![]() .
.
Ainsi, pour tout ![]() on a
on a ![]() , on multiplie par
, on multiplie par ![]() on a
on a
![]()
On intègre sur ![]() selon
selon ![]() avec
avec ![]() les fonctions en jeu sont bien continues, ainsi :
les fonctions en jeu sont bien continues, ainsi :
![Rendered by QuickLaTeX.com \[\underset{\text{\tiny{ind\'{e}pendant de $t$}}}{\underbrace{f\left(\alpha_x\right)}} \int_0^x t\; \text{d}t\leqslant \int_0^x tf(t)\text{d}t\leqslant \underset{\text{\tiny{ind\'{e}pendant de $t$}}}{\underbrace{f\left(\beta_x\right)}} \int_0^x t\; \text{d}t.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f8ebd54a72acf5cbd7151c4c34debf2b_l3.png)
5/ c/ On reprend ce qui précède et on calcule ![]()
Donc
![]()
Donc en divisant par ![]()
![]()
On a ![]() donc par encadrement
donc par encadrement ![]() , par continuité de
, par continuité de ![]() en 0 on a
en 0 on a ![]()
De façon analogue ![]()
Le théorème des gendarmes permet de conclure.
Bilan : ![]()
5/ d/ Soit ![]() Sur le segment
Sur le segment ![]()
![]() est continue donc elle admet un minimum atteint en un point noté
est continue donc elle admet un minimum atteint en un point noté ![]() et un maximum atteint en un point noté
et un maximum atteint en un point noté ![]() .
.
Ainsi, pour tout ![]() on a
on a ![]() , on multiplie par
, on multiplie par ![]() on a
on a
![]()
On intègre sur ![]() selon
selon ![]() avec
avec ![]() les fonctions en jeu sont bien continues, ainsi :
les fonctions en jeu sont bien continues, ainsi :
![Rendered by QuickLaTeX.com \[\underset{\text{\tiny{ind\'ependant de $t$}}}{\underbrace{f\left(\beta_x\right)}} \int_x^0 t\; \text{d}t\leqslant \int_x^0 tf(t)\text{d}t\leqslant \underset{\text{\tiny{ind\'ependant de $t$}}}{\underbrace{f\left(\alpha_x\right)}} \int_x^0 t\; \text{d}t.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-be4f372eac116fae236a3cd3b4b7990f_l3.png)
On inverse les bornes des intégrales en multipliant par ![]()
![]()
On reprend ce qui précède et on calcule ![]()
Donc
![]()
Donc en divisant par ![]()
![]()
On a ![]() donc par encadrement
donc par encadrement ![]() , par continuité de
, par continuité de ![]() en 0 on a
en 0 on a ![]()
De façon analogue ![]()
Le théorème des gendarmes permet de conclure.
Bilan : ![]()
6/ On a : 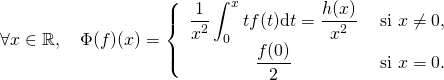
Donc pour ![]() or
or ![]() donc
donc ![]() Donc
Donc ![]() est continue en 0.
est continue en 0.
Sur ![]()
![]() or
or ![]() est
est ![]() sur
sur ![]() et
et ![]() est
est ![]() sur
sur ![]() donc par produit
donc par produit ![]() est
est ![]() donc continue sur
donc continue sur ![]()
De plus pour ![]()
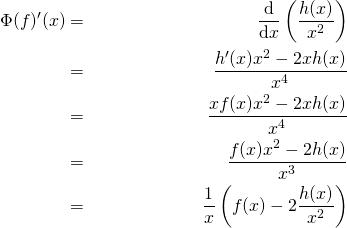
Bilan : ![]() est continue sur
est continue sur ![]() et de classe
et de classe ![]() sur
sur ![]() et sur
et sur ![]() et l’on a :
et l’on a :
![]()
7/ a/ Soit ![]() une fonction paire,
une fonction paire, ![]() est définie sur
est définie sur ![]() et pour tout
et pour tout ![]() on a
on a ![]()
Et, pour ![]()
![]()
On fait le changement de variable affine donc
Ainsi
![]()
Donc
De plus ![]() Donc
Donc ![]() est paire sur
est paire sur ![]()
Soit ![]() une fonction impaire,
une fonction impaire, ![]() est définie sur
est définie sur ![]() et pour tout
et pour tout ![]() on a
on a ![]()
Et, pour ![]()
![]()
On fait le changement de variable affine donc
Ainsi
![]()
Donc
De plus ![]() car
car ![]() est impaire donc
est impaire donc ![]()
Donc ![]() est impaire sur
est impaire sur ![]()
Bilan : si ![]() est une fonction paire (respectivement impaire), alors
est une fonction paire (respectivement impaire), alors ![]() est encore une fonction paire (respectivement impaire).
est encore une fonction paire (respectivement impaire).
7/ b/ Soit ![]() une fonction positive sur
une fonction positive sur ![]()
Pour ![]()
![]()
Pour tout
Pour ![]()
![]()
Pour tout
Enfin ![]()
Bilan : si ![]() est une fonction positive, alors
est une fonction positive, alors ![]() est encore une fonction positive.
est encore une fonction positive.
8/ a/ On admet le résultat suivant :
![]()
Or pour ![]() ,
,
![]()
= ![]()
= ![]()
= ![]()
Or ![]() donc
donc ![]()
Bilan :![]()
8/ b/ Soit ![]()
On suppose ![]() On pose
On pose ![]() donc
donc ![]() En appliquant le résultat précédent,
En appliquant le résultat précédent, ![]()
Or pour ![]() ,
, ![]()
On refait le changement de variable ![]()
![]()
Or ![]() donc
donc ![]() donc
donc ![]()
Bilan :![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie C. Une application en probabilité
9/ Soit ![]() on sait que
on sait que ![]() est une fonction de répartition de loi à densité donc elle est continue, croissante et positive sur
est une fonction de répartition de loi à densité donc elle est continue, croissante et positive sur ![]() donc, pour tout
donc, pour tout ![]() on a
on a ![]() on multiplie par
on multiplie par ![]() et
et ![]()
On intègre sur ![]() selon
selon ![]() avec
avec ![]() les fonctions en jeu sont bien continues ainsi
les fonctions en jeu sont bien continues ainsi
![Rendered by QuickLaTeX.com \[0\leqslant \int_0^x tF(t)\text{d}t \leqslant \underset{\text{\tiny{ind\'ependant de $t$}}}{\underbrace{F(x)}}\int_0^x t\text{d}t=F(x)\left[\frac{t^2}{2}\right]_0^x= \frac{x^2F(x)}{2}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3720d4a67a3665bb18010057513f7ba5_l3.png)
On multiplie par
Soit ![]() on sait déjà que
on sait déjà que ![]() est continue, croissante sur
est continue, croissante sur ![]() donc, pour tout
donc, pour tout ![]() on a
on a ![]() on multiplie par
on multiplie par ![]() et
et ![]()
On intègre sur ![]() selon
selon ![]() avec
avec ![]() ainsi
ainsi
![Rendered by QuickLaTeX.com \[\int_x^0 tF(t)\text{d}t \leqslant \underset{\text{\tiny{ind\'ependant de $t$}}}{\underbrace{F(x)}}\int_x^0 t\text{d}t = -\frac{x^2F(x)}{2}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-36256fed4804713da7790f5abde955a7_l3.png)
On multiplie par ![]() le signe – est utilisé pour inverser les bornes de l’intégrale
le signe – est utilisé pour inverser les bornes de l’intégrale ![]() et on a bien
et on a bien ![]() .
.
Bilan : ![]() et
et ![]()
10/ On sait que ![]() et
et ![]() sont continues sur
sont continues sur ![]() donc par produit
donc par produit ![]() est continue sur
est continue sur ![]() donc elle admet une primitive que l’on note
donc elle admet une primitive que l’on note ![]() qui est donc
qui est donc ![]() sur
sur ![]() . Ainsi pour tout
. Ainsi pour tout ![]() on a
on a ![]()
Les fonctions ![]() et
et ![]() sont
sont ![]() sur
sur ![]() donc
donc ![]() l’est aussi et
l’est aussi et
![]()
Bilan : ![]() est de classe
est de classe ![]() sur
sur ![]() et sur
et sur ![]() et, pour tout
et, pour tout ![]() de
de ![]()
11/ On considère la fonction ![]() définie sur
définie sur ![]() par :
par : ![]()
[
Soit ![]() on a vu que
on a vu que ![]() donc
donc ![]() on multiplie par
on multiplie par ![]() et
et ![]()
Soit ![]() on a vu que
on a vu que ![]() donc
donc ![]() on multiplie par
on multiplie par ![]() et
et ![]()
Enfin ![]() donc
donc ![]() est bien positive sur
est bien positive sur ![]()
[![]() ] Il reste à établir que
] Il reste à établir que ![]() converge et vaut 1.
converge et vaut 1.
Prenons ![]() , la fonction
, la fonction ![]() est continue sur le segment
est continue sur le segment ![]() et
et ![]() Or la fonction
Or la fonction ![]() (avec
(avec ![]() continue sur
continue sur ![]() ) est continue sur
) est continue sur ![]() donc en particulier en 0 donc
donc en particulier en 0 donc ![]() converge et vaut
converge et vaut ![]() .
.
Comme ![]() est une fonction de répartition, on sait que
est une fonction de répartition, on sait que ![]() , ainsi d’après ce qui précède,
, ainsi d’après ce qui précède,
![]()
donc ![]() converge et vaut
converge et vaut ![]() .
.
Prenons ![]() , la fonction
, la fonction ![]() est continue sur le segment
est continue sur le segment ![]() et
et ![]() Or selon la question, la fonction
Or selon la question, la fonction ![]() (avec
(avec ![]() continue sur
continue sur ![]() ) est continue sur
) est continue sur ![]() donc en particulier en 0 donc
donc en particulier en 0 donc ![]() converge et vaut
converge et vaut ![]() .
.
Comme ![]() est une fonction de répartition, on sait que
est une fonction de répartition, on sait que ![]() , ainsi d’après ce qui précède
, ainsi d’après ce qui précède
![]()
donc ![]() converge et vaut
converge et vaut ![]() .
.
Par la relation de Chasles des intégrales convergentes, ![]() converge et vaut
converge et vaut
![]()
Donc ![]() est bien une densité de probabiité.
est bien une densité de probabiité.
Dans le raisonnement qui précède il est vu que ![]() est
est ![]() sur
sur ![]() que
que ![]() est continue sur
est continue sur ![]() . De plus
. De plus ![]() est positive sur
est positive sur ![]() donc
donc ![]() est croissante sur
est croissante sur ![]() , de même
, de même ![]() est croissante sur
est croissante sur ![]() donc, par continuité en 0,
donc, par continuité en 0, ![]() est croissante sur
est croissante sur ![]() Il a été vu aussi que
Il a été vu aussi que ![]() et
et ![]() .
.
Donc ![]() peut être considérée comme une fonction de répartition d’une variable aléatoire
peut être considérée comme une fonction de répartition d’une variable aléatoire ![]() .
.
On remarque que ![]() et
et ![]() coincide sur
coincide sur ![]() donc
donc ![]() est une densité de probabilité de
est une densité de probabilité de ![]()
Bilan : ![]() est une densité de probabilité d’une variable aléatoire
est une densité de probabilité d’une variable aléatoire ![]() et
et ![]() est la fonction de répartition de
est la fonction de répartition de ![]()
12/ a/ On définit la fonction ![]() sur
sur ![]() par :
par : ![]()
[
Sur
[
![]()
Donc
Bilan : ![]() est une densité de probabilité.
est une densité de probabilité.
12/ b/ Soit ![]() une variable aléatoire admettant
une variable aléatoire admettant ![]() pour densité.
pour densité.
![]() est à densité donc
est à densité donc ![]() admet une espérance si et seulement si
admet une espérance si et seulement si ![]() converge absolument. Comme
converge absolument. Comme ![]() est nulle sur
est nulle sur ![]() cela revient à montrer que
cela revient à montrer que ![]() converge absolument. Cela équivaut encore à
converge absolument. Cela équivaut encore à ![]() converge absolument. La fonction sous cette intégrale est positive donc convergence absolue équivaut à convergence.
converge absolument. La fonction sous cette intégrale est positive donc convergence absolue équivaut à convergence.
On pense à exploiter le moment d’ordre 2 d’une loi normale centrée réduite d’une variable ![]() qui vaut
qui vaut ![]() autrement dit
autrement dit
![]()
La fonction
![]()
Cela suggère le changement de variable affine
Les bornes sont inchangées et ![]() donc
donc
![]()
Donc
![]()
Bilan : ![]() admet une espérance et
admet une espérance et ![]()
12/ c/ On note ![]() la fonction de répartition de
la fonction de répartition de ![]() et on pose
et on pose ![]()
D’après ce qui précède, ![]() est nulle sur
est nulle sur ![]() comme
comme ![]() Soit
Soit ![]()
![]()
Ensuite

Donc pour ![]() on a
on a ![]() donc
donc ![]() donc
donc ![]()
Puis ![]()
Enfin pour ![]() on a
on a ![]() donc
donc
![]()
Bilan : 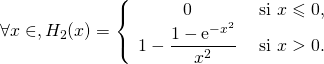
D’après la question 11/, ![]() est la fonction de répartition d’une variable aléatoire à densité que l’on note
est la fonction de répartition d’une variable aléatoire à densité que l’on note ![]()
Pour déterminer une densité ![]() de
de ![]() il suffit de dériver
il suffit de dériver ![]() là où elle est
là où elle est ![]() et d’imposer des valeurs là où elle n’est a priori pas
et d’imposer des valeurs là où elle n’est a priori pas ![]() .
.
Ici ![]() est
est ![]() sur
sur ![]() on propose
on propose
![Rendered by QuickLaTeX.com \[h_2(x)=\left\{\begin{array}{cl} 0 & \text{ si } x\leqslant 0,\\\displaystyle\displaystyle \frac{-2x^3\text{e}^{-x^2}-2x(\text{e}^{-x^2}-1)}{x^4} = \frac{-2x^2\text{e}^{-x^2}-2\text{e}^{-x^2}+2}{x^3}& \text{ si } x > 0.\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-70f31c1523a00a4f84cefb0e8fe87f6b_l3.png)
Montrer que ![]() admet une espérance revient à montrer que
admet une espérance revient à montrer que ![]() converge absolument. Comme
converge absolument. Comme ![]() est nulle sur
est nulle sur ![]() cela revient à montrer que
cela revient à montrer que ![]() converge absolument. La fonction sous cette intégrale est positive donc convergence absolue équivaut à convergence.
converge absolument. La fonction sous cette intégrale est positive donc convergence absolue équivaut à convergence.
On remarque que, pour ![]() on a
on a ![]() .
.
Avec le changement de variable ![]() on montre comme ci-dessus que
on montre comme ci-dessus que ![]() converge en faisant apparaître une densité de loi normale centrée réduite. Il reste à montrer que
converge en faisant apparaître une densité de loi normale centrée réduite. Il reste à montrer que ![]() converge.
converge.
La fonction ![]() est continue, positive sur
est continue, positive sur ![]() , avec
, avec ![]() on a
on a ![]() car
car ![]()
Donc ![]() est faussement impropre en 0.
est faussement impropre en 0.
On a aussi ![]() donc comme
donc comme ![]() on a
on a ![]() donc
donc ![]() .
.
Or l’intégrale de Riemann ![]() converge donc, par comparaison d’intégrale de fonctions psoitives, l’intégrale
converge donc, par comparaison d’intégrale de fonctions psoitives, l’intégrale ![]() converge.
converge.
Par somme ![]() converge et
converge et ![]() a une espérance.
a une espérance.
Partie D. Étude d’un espace vectoriel et d’un produit scalaire
13/ a/ Pour tout ![]() on a
on a ![]() donc
donc ![]() donc
donc ![]()
De même ![]() donc
donc ![]() donc
donc ![]()
Donc ![]()
![]() domine
domine ![]() et
et ![]() donc il domine
donc il domine ![]()
Bilan : ![]()
13/ b/ Soit ![]() et
et ![]() dans
dans ![]() on a, pour tout
on a, pour tout ![]()
Or ![]() et
et ![]() convergent donc par domination de fonctions positives et continues
convergent donc par domination de fonctions positives et continues ![]() converge donc
converge donc ![]() est absolument convergente.
est absolument convergente.
Bilan : Pour toutes fonctions ![]() et
et ![]() de
de ![]() l’intégrale
l’intégrale ![]() est absolument convergente.
est absolument convergente.
14/
[[
[
Bilan : ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]()
15/
[[
[
![]()
par linéarité des intégrales convergentes. Donc
[
![]()
car on intègre une fonction positive avec des bornes d’intégration dans l’ordre croissant.
[
Réciproquement si ![]() alors
alors ![]() .
.
La fonction ![]() est continue sur
est continue sur ![]() donc elle y admet une primitive qu’on note
donc elle y admet une primitive qu’on note ![]() on a alors
on a alors
![]()
Or ![]() est positive sur
est positive sur ![]() donc
donc ![]() est croissante sur
est croissante sur ![]() donc, pour tout
donc, pour tout ![]() on a
on a ![]() donc
donc ![]() est constante sur
est constante sur ![]() donc sa dérivée est nulle donc
donc sa dérivée est nulle donc ![]() est nulle sur
est nulle sur ![]()
Bilan : ![]() est un produit scalaire de
est un produit scalaire de ![]()
16/ a/ Il a été vu que ![]() La fonction carrée est continue sur
La fonction carrée est continue sur ![]() , donc par composition
, donc par composition 
Il a été vu que ![]() La fonction carrée est continue sur
La fonction carrée est continue sur ![]() , donc par composition
, donc par composition 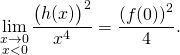
16/ b/ On fait une intégration par parties, on pose
![]()
Les fonctions ![]() et
et ![]() sont
sont ![]() sur
sur ![]() on fixe
on fixe ![]() et
et
on a
![Rendered by QuickLaTeX.com \[\forall X>0,\int_a^{X}\frac{\big(h(x)\big)^2}{x^4}\text{d}x= \left[ \frac{-1}{3}x^{-3}\left({h(x)}\right)^2\right]_a^X - \int_a^{X}\frac{-1}{3x^{3}} 2xf(x)h(x)\text{d}x\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-fae2266318ead57a73fe2de9fbf72d0a_l3.png)
![Rendered by QuickLaTeX.com \[=\frac{-1}{3X^{3}}\left({h(X)}\right)^2-\frac{-1}{3a^{3}}\left({h(a)}\right)^2+\frac23\int_a^{X}f(x)\frac{h(x)}{x^2}\text{d}x$ =$\frac{-1}{3X^{3}}\left({h(X)}\right)^2-\frac{-1}{3a^{3}}\left({h(a)}\right)^2+\frac23\int_a^{X}f(x)\Phi(f)(x)\text{d}x.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0e5238ec02dd34eb9b4d8a2d08fc26a7_l3.png)
Il reste à étudier la convergence lorsque ![]() On a
On a ![]()
La question 6. assure que ![]() est continue en 0 donc
est continue en 0 donc ![]() l’est aussi et
l’est aussi et ![]() converge ou existe.
converge ou existe.
Bilan :
![]()
16/ c/ Soit ![]() La fonction polynomiale
La fonction polynomiale ![]() est positive sur
est positive sur ![]() car une intégrale d’une fonction positive avec des bornes dans l’ordre croissant est positive. Elle peut s’écrire
car une intégrale d’une fonction positive avec des bornes dans l’ordre croissant est positive. Elle peut s’écrire
![]()
Si ![]() alors on a déjà vu que
alors on a déjà vu que ![]() est nulle sur
est nulle sur ![]() donc
donc
![Rendered by QuickLaTeX.com \[\int_0^{X}f(x)\Phi(f)(x)\text{d}x=0= \left(\int_0^{X}\big(f(x)\big)^2\text{d}x\right)^{1/2} \left(\int_0^{X}\big(\Phi(f)(x)\big)^2\text{d}x\right)^{1/2}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b7fdfc8e6a64adc9d1caeb8a4fcc55e5_l3.png)
Si ![]() , alors la fonction polynomiale
, alors la fonction polynomiale ![]() est de degré 2 et elle est de signe constant sur
est de degré 2 et elle est de signe constant sur ![]() donc elle ne peut pas avoir deux racines réelles distinctes sinon il y a changement de signe. Donc le discriminant est négatif ou nul donc
donc elle ne peut pas avoir deux racines réelles distinctes sinon il y a changement de signe. Donc le discriminant est négatif ou nul donc
![]()
Donc en divisant par 4>0,
![]()
On compose par racine carrée qui est croissante sur ![]() les deux intégrales
les deux intégrales ![]() sont positives.
sont positives.
![Rendered by QuickLaTeX.com \[\left\vert\int_0^{X}f(x)\Phi(f)(x)\text{d}x\right\vert \leqslant \left(\int_0^{X}f^2(x)\text{d}x\right)^{1/2}\left(\int_0^{X}\Phi(f)(x)^2(x)\text{d}x\right)^{1/2}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-45bb4855bfbc2707530a856e6eed5ac5_l3.png)
Bilan :
![Rendered by QuickLaTeX.com \[\int_0^{X}f(x)\Phi(f)(x)\text{d}x\leqslant \left(\int_0^{X}\big(f(x)\big)^2\text{d}x\right)^{1/2} \left(\int_0^{X}\big(\Phi(f)(x)\big)^2\text{d}x\right)^{1/2}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3d6f37ab0dfc2b3963d66fa46039eb35_l3.png)
16/ d/ Soit ![]() on multiplie ce qui précède par
on multiplie ce qui précède par ![]()
![Rendered by QuickLaTeX.com \[\frac23\int_0^{X}f(x)\Phi(f)(x)\text{d}x\leqslant \frac23\left(\int_0^{X}\big(f(x)\big)^2\text{d}x\right)^{1/2} \left(\int_0^{X}\big(\Phi(f)(x)\big)^2\text{d}x\right)^{1/2}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9a2ca5af87d8a37b2804b8eea6f46221_l3.png)
On reprend la question 16/b/, qui donne
![Rendered by QuickLaTeX.com \[\int_0^{X}\frac{\big(h(x)\big)^2}{x^4}\text{d}x= \int_0^{X}{\big(\Phi(f)(x)\big)^2}\text{d}x=\underset{ \leqslant 0}{\underbrace{-\frac{1}{3}\frac{\big(h(X)\big)^2}{X^3}}}+\frac23\int_0^{X}f(x)\Phi(f)(x)\text{d}x\leqslant \frac23\int_0^{X}f(x)\Phi(f)(x)\text{d}x.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-de9a80b72ac4bd88540a578d93c74fc8_l3.png)
Donc
![Rendered by QuickLaTeX.com \[\int_0^{X}\big(\Phi(f)(x)\big)^2\text{d}x\leqslant \frac23\int_0^{X}f(x)\Phi(f)(x)\text{d}x\leqslant\frac23\left(\int_0^{X}\big(f(x)\big)^2\text{d}x\right)^{1/2} \left(\int_0^{X}\big(\Phi(f)(x)\big)^2\text{d}x\right)^{1/2}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c4752843b2418b559263d808804a8fdb_l3.png)
Si  alors comme
alors comme 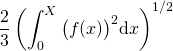 est positive, on pourra conclure.
est positive, on pourra conclure.
Si 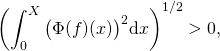 alors on pourra diviser ce qui précède par cette quantité et on pourra conclure aussi.
alors on pourra diviser ce qui précède par cette quantité et on pourra conclure aussi.
Bilan : 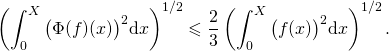
16/ e/ On compose ce qui précède par la fonction ![]() croissante sur
croissante sur ![]() et on a
et on a ![]()
Or ![]() donc
donc
![]()
et
![]()
La fonction ![]() est continue sur
est continue sur ![]() donc la fonction
donc la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() avec une dérivée
avec une dérivée ![]() positive donc
positive donc ![]() est croissante sur
est croissante sur ![]() . On a montré qu’elle est majorée sur
. On a montré qu’elle est majorée sur ![]() par
par ![]() (indépendant de
(indépendant de ![]() ) donc
) donc ![]() a une limite finie en
a une limite finie en ![]() Donc
Donc ![]() converge.
converge.
En faisant tendre ![]() vers
vers ![]() dans la relation du 16/d/, on a
dans la relation du 16/d/, on a
![Rendered by QuickLaTeX.com \[\displaystyle\left(\int_0^{+\infty}\big(\Phi(f)(x)\big)^2\text{d}x\right)^{1/2}\leqslant \frac23\left(\int_0^{+\infty}\big(f(x)\big)^2\text{d}x\right)^{1/2}\text{ donc } \sqrt{\langle \Phi(f),\Phi(f)\rangle}\leqslant\frac23 \sqrt{\langle f,f\rangle}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9703c109aa4b001c2b35cca990069277_l3.png)
Bilan : La fonction ![]() appartient à
appartient à ![]() et
et ![]()
16/ f/ Soit ![]() en utilisant la relation de la question 16.b, on a
en utilisant la relation de la question 16.b, on a
![]()
or les deux intégrales
Notons ![]() cette limite, elle est positive car
cette limite, elle est positive car ![]() positive sur
positive sur ![]() Si
Si ![]() est non nulle alors
est non nulle alors
![Rendered by QuickLaTeX.com \[\frac{X\Big(\Phi(f)(X)\Big)^2}{\alpha}\underset{X\to+\infty}{\longrightarrow} 1\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1719a1399793d24077ab56e84bdbc8d4_l3.png)
donc
Or ![]() diverge, cela contredit le fait que
diverge, cela contredit le fait que ![]() Donc
Donc ![]() est nulle.
est nulle.
Bilan : La limite de ![]() en
en ![]() est 0.
est 0.
16/ g/ Avec la question 16.b,
![]()
Donc en faisant tendre ![]() vers
vers ![]() on a
on a
![]()
Bilan : ![]()
Partie E. Etude d’une suite
17/ function v=suite_v(n)
S=0
for k=1:n
S=S+k*suite_u(k)
end
v = 1/(n*(n+1))*S
endfunction
18/ a/ La suite ![]() est positive, décroissante donc elle converge.
est positive, décroissante donc elle converge.
18/ b/ D’après les graphiques, ![]() semble décroissante, convergente avec une limite moitié moindre que celle de
semble décroissante, convergente avec une limite moitié moindre que celle de ![]() .
.
18/ c/ Pour tout ![]() de
de ![]() , on a, pour tout
, on a, pour tout ![]() donc
donc ![]() donc
donc ![]() donc
donc ![]() donc
donc ![]()
D’autre part
![Rendered by QuickLaTeX.com \[v_{2n} = \frac{1}{2n(2n+1)}\sum\limits_{k=1}^{2n}ku_k= \frac{1}{2n(2n+1)}\underset{= n(n+1)v_n}{\underbrace{\sum\limits_{k=1}^{n}ku_k}} + \frac{1}{2n(2n+1)}\sum\limits_{k=n+1}^{2n}ku_k.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-eeff953abd4b0ae29403e015e6d548d1_l3.png)
Donc
![Rendered by QuickLaTeX.com \[v_{2n} = \frac{1}{2n(2n+1)}\times\Big(n(n+1)v_n\Big)+\frac{1}{2n(2n+1)}\sum\limits_{k=n+1}^{2n}ku_k.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a95d73a62754a0d8c8670d11dd80a05e_l3.png)
Comme la suite
Or ![]()
= ![]()
= ![]()
= ![]()
Cela permet de conclure
![]()
18/ d/ Pour tout ![]() de
de ![]() :
:
![Rendered by QuickLaTeX.com \[(n+2)v_{n+1}= (n+2)\frac{1}{(n+1)(n+2)}\sum\limits_{k=1}^{n+1}ku_k = \frac{1}{n+1}\left(\sum\limits_{k=1}^{n}ku_k+(n+1)u_{n+1}\right) =\frac{1}{n+1} \sum\limits_{k=1}^{n}ku_k+ u_{n+1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-749cb040294c1f2d3eec848774e71481_l3.png)
![Rendered by QuickLaTeX.com \[=n\frac{1}{n(n+1)} \sum\limits_{k=1}^{n}ku_k+ u_{n+1}=nv_n+u_{n+1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f6d58327736a5e710e5b74e238062ac0_l3.png)
D’autre part
![Rendered by QuickLaTeX.com \[v_{n+1}-v_n= v_{n+1} -\frac{1}{(n+1)n}\sum\limits_{k=1}^{n}ku_k = v_{n+1} -\frac{1}{(n+1)n}\Big(\underset{=(n+1)(n+2)v_{n+1}}{\underbrace{\sum\limits_{k=1}^{n+1}ku_k}}-(n+1)u_{n+1}\Big)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-17d0c3621e758dd31e8f6fff6ea1f71e_l3.png)
![]()
18/ e/ Soit ![]() on a
on a ![]() donc
donc ![]() donc
donc ![]() donc la suite
donc la suite ![]() est décroissante. Chaque
est décroissante. Chaque ![]() est une somme de réels positifs donc la suite est minorée par 0 donc elle converge.
est une somme de réels positifs donc la suite est minorée par 0 donc elle converge.
On pose ![]() et
et ![]() , la relation
, la relation ![]() vraie pour tout
vraie pour tout ![]() donne
donne ![]()
On utilise ensuite la relation ![]()
On sait qu’un polynôme est équivalent à son terme dominant en ![]() donc
donc ![]() et
et ![]()
Donc par passage à la limite ![]() donc
donc ![]() donc
donc ![]() .
.
Enfin ![]() .
.
19/ a/ Pour tout ![]() on pose
on pose ![]()
Au rang 1, on a ![]() Donc
Donc ![]() est vraie.
est vraie.
Supposons ![]() vraie à un rang
vraie à un rang ![]()
on a
![Rendered by QuickLaTeX.com \[\sum\limits_{n= 1}^{N+1} v_n = v_{N+1} +\sum\limits_{n= 1}^N v_n =v_{N+1}+\sum\limits_{k=1}^N u_k-Nv_N\text{ selon } {\cal H}_N.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a923d193f62b8b1f9270e0b898a21802_l3.png)
On exploite la question 18/d/, pour obtenir
Ainsi
![Rendered by QuickLaTeX.com \[\sum\limits_{n= 1}^{N+1} v_n =v_{N+1}+\sum\limits_{k=1}^N u_k-(N+2)v_{N+1}+u_{N+1}=\sum\limits_{k=1}^{N+1} u_k-(N+1)v_{N+1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4915257e6a1b6fd00f8ecd4df252c5d4_l3.png)
Donc
Bilan : Pour tout ![]()
![]() est vraie et
est vraie et ![]()
19/ b/ La série ![]() est à terme général positif donc ses sommes partielles forment une suite croissante. Celle-ci converge donc si et seulement elle est majorée.
est à terme général positif donc ses sommes partielles forment une suite croissante. Celle-ci converge donc si et seulement elle est majorée.
Or, pour tout ![]()
![]() car
car ![]()
Comme ![]() est à terme positif, on a
est à terme positif, on a ![]()
Donc, pour tout ![]()
![]() , ce dernier terme est indépendant de
, ce dernier terme est indépendant de ![]() donc il domine les sommes partielles de la série
donc il domine les sommes partielles de la série ![]()
Bilan : ![]() converge.
converge.
19/ c/ Pour tout ![]()
![]() .
.
Or les séries ![]() et
et ![]() convergent donc la suite
convergent donc la suite ![]() converge.
converge.
Donc ![]() tend vers une limite finie
tend vers une limite finie ![]() lorsque l’entier
lorsque l’entier ![]() tend vers
tend vers ![]() .
.
La suite ![]() est à terme positif donc
est à terme positif donc ![]()
Si ![]() alors
alors ![]() donc
donc ![]() Or la série
Or la série ![]() diverge comme combinaison linéaire de série harmonique avec
diverge comme combinaison linéaire de série harmonique avec ![]() . Par comparaison des séries à terme général positif,
. Par comparaison des séries à terme général positif, ![]() diverge aussi, cela contredit ce qui précède. Donc
diverge aussi, cela contredit ce qui précède. Donc ![]()
19/ d/ Au 19.a, il est vu que, pour tout ![]()
![]() Comme
Comme ![]() on peut conclure
on peut conclure![]()
20/ a/ On reprend ce qui précède, avec pour tout ![]() et
et ![]() Donc les conditions sont réunies pour affirmer qu’avec
Donc les conditions sont réunies pour affirmer qu’avec ![]() on a, pour tout
on a, pour tout ![]() et
et ![]() c’est-à-dire
c’est-à-dire ![]()
Bilan : Il existe une variable aléatoire ![]() à valeurs dans
à valeurs dans ![]() telle que :
telle que :
![Rendered by QuickLaTeX.com \[\forall n\in\N^*, {\bf P}(Z=n)=\frac{1}{n(n+1)}\sum\limits_{k=1}^nk{\bf P}(Y=k).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6e55e967501d3e2046b79ad8addefc0c_l3.png)
20/ b/ On suppose dans cette question que ![]() admet une espérance, notée
admet une espérance, notée ![]() Cette espérance est strictement positive car
Cette espérance est strictement positive car ![]() est à support dans
est à support dans ![]()
Donc comme ![]() , on a
, on a
![Rendered by QuickLaTeX.com \[\frac{\sum\limits_{k=1}^nk{\bf P}(Y=k)}{ {\bf E}(Y)}\underset{n\to +\infty}{\longrightarrow} 1\text{ donc } \sum\limits_{k=1}^nk{\bf P}(Y=k)\underset{n\to +\infty}{\sim} {\bf E}(Y).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d610d91737b4f9cc7821d93ef227aa04_l3.png)
D’autre part ![]() donc par produit
donc par produit ![]()
Cela entraîne ![]()
La série ![]() diverge donc la série
diverge donc la série ![]() diverge car
diverge car ![]()
Donc par comparaison des séries à terme général positif, la série ![]() diverge donc la variable aléatoire
diverge donc la variable aléatoire ![]() n’a pas d’espérance.
n’a pas d’espérance.

