Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet HEC-ESCP Maths 2 ECS 2018
Revenir à tous les corrigés des annales maths BCE
Partie I : Séries téléscopiques
1/ a/ La série ![]() est convergente car son terme général est positif et équivalent au terme général d’une série de Riemann convergente
est convergente car son terme général est positif et équivalent au terme général d’une série de Riemann convergente ![]()
En écrivant, pour tout ![]() :
: ![]()
On obtient une somme télescopique :
![]()
La somme de la série ![]() est donc égale à 1.
est donc égale à 1.
b/ Avec la décomposition de fractions trouvée, on reconnaît pour ![]() la loi certaine égale à 1.
la loi certaine égale à 1.
2/ a/ La fonction ![]() est positive lorsque
est positive lorsque ![]() et continue sur
et continue sur ![]() privé d’un nombre fini de points
privé d’un nombre fini de points
Calculons l’intégrale de ![]() sur
sur ![]() :
:
![]()
= ![]()
![]()
= ![Rendered by QuickLaTeX.com \dfrac1{n+1}+\left[\dfrac{n+1}2x^2\right]_{-\tfrac1{n+1}}^0](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-518eb17ae2032f686f84edfc4abf97ea_l3.png)
= ![]()
![]()
![]()
= ![Rendered by QuickLaTeX.com (n+1)\left[x-\dfrac{x^2}2\right]_{\tfrac n{n+1}}^1](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-af9695c4ebfc0701c8c503862edbc254_l3.png)
= ![]()
= ![]()
On a donc :
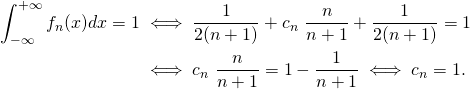
La fonction ![]() est donc une densité de probabilité si et seulement si
est donc une densité de probabilité si et seulement si ![]() .
.
Pour ![]() :
:
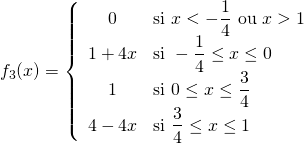 .
.
b/ Puisque ![]() est nulle en dehors de
est nulle en dehors de ![]() , la fonction de répartition
, la fonction de répartition ![]() de
de ![]() est :
est :
nulle sur ![]() ,
,
égale à 1 sur ![]() .
.
pour ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*}F_n(x)& = \int_{-\tfrac1{n+1}}^x\big(1+(n+1)t\big)dt = \left[t+\dfrac{n+1}2t^2\right]_{-\tfrac1{n+1}}^x\\ &= x+\dfrac{n+1}2x^2-\left(-\dfrac1{n+1}+\dfrac{n+1}2\left(-\dfrac1{n+1}\right)^2\right)\\ &=\dfrac1{2(n+1)}+x+\dfrac{n+1}2x^2 \end{align*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cd6ce5ced14142e063eab3179111c41f_l3.png)
pour ![]() :
:
![]()
pour ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*}F_n(x)&=F_n\left(\dfrac n{n+1}\right) + \int_{\tfrac n{n+1}}^x (n+1)(1-t)dt = \dfrac{1+2n}{2(1+n)} + \left[(n+1)\left(t-\dfrac{t^2}2\right)\right]_{\tfrac n{n+1}}^x\\ &=\dfrac{1+2n}{2(1+n)} +(n+1)\left(\left(x-\dfrac{x^2}2\right)-\dfrac n{n+1}\left(1-\dfrac n{2(n+1)}\right)\right)\\ &=\dfrac{1-n}2+(n+1)x-\dfrac{n+1}2x^2. \end{align*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-42e284593dfcb5dabcaeb05fc39f0c83_l3.png)
Conclusion :
![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},~ F_n(x)=\left\{\begin{array}{clrcl} 0&\text{si }&&x&\leq-\dfrac1{n+1}\\[0.75em] \dfrac1{2(n+1)}+x+\dfrac{n+1}2x^2&\text{si }&-\dfrac1{n+1}\leq &x&\leq 0\\[0.75em] \dfrac1{2(n+1)}+x&\text{si }&0\leq &x&\leq \dfrac n{n+1}\\[0.75em] \dfrac{1-n}2+(n+1)x-\dfrac{n+1}2x^2&\text{si }&\dfrac n{n+1}\leq &x& \leq 1\\[0.75em] 1&\text{si }&1\leq&x\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0e35c3b0e25080e0a330a5ee05267e64_l3.png)
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() car
car ![]() est continue sur
est continue sur ![]() .
.
c/ Si ![]() , alors, comme
, alors, comme ![]() :
:
![]()
Si ![]() alors de même :
alors de même :
![]()
Si ![]() , alors :~
, alors :~ ![]() .
.
Conclusion :
![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},~ F_n(x)\tendinf \xrightarrow n\left\{\begin{array}{cl} 0& \text{si }0\leq x\\ x&\text{si }0\leq x \leq 1\\ 1&\text{si }x\geq 1 \end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7b159610179f71d75fdbe5be7758452e_l3.png)
ce qui prouve la convergence en loi de ![]() vers une variable aléatoire
vers une variable aléatoire ![]() .
.
3/ a/ Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\P\left(\left|\dfrac{X_{n+1}}{n+1}\right|\geq \varepsilon\right) = 1-\underbrace{F\big(\varepsilon(n+1)\big)}_{\displaystyle\tendinf \xrightarrow n 0} + \underbrace{F\big(-\varepsilon(n+1)\big)}_{\displaystyle\tendinf n1}\tendinf \xrightarrow n 0.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-90c46d3890bffd2232657f12b709e5eb_l3.png)
(où ![]() est la fonction de répartition de
est la fonction de répartition de ![]() (donc aussi celle de
(donc aussi celle de ![]() ))\\
))\\
ce qui prouve la convergence en probabilité de ![]() vers 0.
vers 0.
b/ Comme ![]() et
et ![]() , le théorème de Slutsky donne la convergence en loi de la suite de variables aléatoires
, le théorème de Slutsky donne la convergence en loi de la suite de variables aléatoires ![]() vers
vers ![]() .
.
c/ En remarquant que :
![]()
on obtient une densité de la variable aléatoire ![]() :
:
![]()
L’indépendance des variables ![]() et
et ![]() permet alors d’utiliser le produit de convolution pour obtenir une densité
permet alors d’utiliser le produit de convolution pour obtenir une densité ![]() de
de ![]() en notant que,
en notant que, ![]() étant bornée, la fonction
étant bornée, la fonction ![]() ci-dessous est bien définie et continue sauf en un nombre fini de points:
ci-dessous est bien définie et continue sauf en un nombre fini de points:
![]()
d/ Supposons que ![]() suive la loi uniforme sur
suive la loi uniforme sur ![]() . On peut choisir la densité :
. On peut choisir la densité :
![Rendered by QuickLaTeX.com \[f:\left\{\begin{array}{rcl} \mathbb{R}&\to&\mathbb{R} \\ x&\mapsto&\left\{\begin{array}{cl} 1&\text{si }x\in[0,1]\\ 0&\text{sinon} \end{array}\right. \end{array}\right..\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-58942eddba1a2fd641e1f1b4541fc13f_l3.png)
qui est bornée
La question (c) donne une densité de ![]() ; or :
; or :
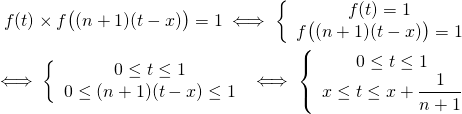
et ![]() sinon.\\
sinon.\\
On est donc amené à déterminer l’intersection
![]()
qui est un intervalle borné (comme intersection de deux intervalles bornés), éventuellement vide, et dont on note ![]() la longueur (différence entre les deux bornes si l’intervalle est d’intérieur non vide ; nulle s’il est vide ou réduit à un point).
la longueur (différence entre les deux bornes si l’intervalle est d’intérieur non vide ; nulle s’il est vide ou réduit à un point).
On aura alors :
![]()
Il s’agit de la densité ![]() de la question 2.
de la question 2.
D’après (b), ![]() converge en loi vers la variable
converge en loi vers la variable ![]() .
.
On a donc retrouvé le résultat de la question 2.(c).
4/ a/ Les deux variables aléatoires ![]() et
et ![]() vérifient une loi normale (chacune transformée affine d’une variable aléatoire suivant une loi normale).\\ Elles sont de plus indépendantes, donc par stabilité additive de la loi normale,
vérifient une loi normale (chacune transformée affine d’une variable aléatoire suivant une loi normale).\\ Elles sont de plus indépendantes, donc par stabilité additive de la loi normale, ![]() suit une loi normale, de paramètres :
suit une loi normale, de paramètres :
![]()
![]()
b/ Avec les notations de la question 3.:
![Rendered by QuickLaTeX.com \[\sum_{n=1}^N U_n=X_1-\dfrac{X_{N+1}}{N+1}=D_N\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7a67b80cc38c987ad7ab8b4f310c1295_l3.png)
La variable aléatoire ![]() possède une densité bornée, donc d’après 3.(b), la suite
possède une densité bornée, donc d’après 3.(b), la suite ![]() converge en loi vers
converge en loi vers ![]() .\\ La série
.\\ La série ![]() converge donc en loi vers
converge donc en loi vers ![]() .
.
c/ Par indépendance des variables aléatoires ![]() (
(![]() ) et par stabilité additive de la loi normale :
) et par stabilité additive de la loi normale :
![Rendered by QuickLaTeX.com \[T_n^\prime\hookrightarrow \mathcal N\left(0,{\sigma_n}^2\right) \quad\text{ avec }\sigma_n=\sqrt{\sum_{k=1}^n \dfrac1{k^2}+\dfrac1{(k+1)^2}}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-05d19d0189008a953410fca5666d0413_l3.png)
La fonction de répartition de ![]() est donnée par :
est donnée par :
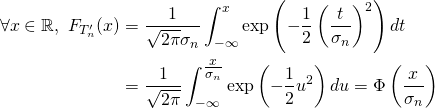
(avec le changement de variable ![]() ).\\
).\\
Par ailleurs:
![Rendered by QuickLaTeX.com \[{\sigma_n}^2= 2\sum_{k=1}^{n+1} \dfrac1{k^2} - 1 \xrightarrow[n\to+\infty]{} \zeta(2)-1=\dfrac{\pi^2}3-1.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7d8c4f855115cd9c57410d37ba81d611_l3.png)
Par continuité de ![]() (sur
(sur ![]() ):
):
![]()
ce qui prouve que la suite ![]() converge en loi vers une variable aléatoire de loi normale
converge en loi vers une variable aléatoire de loi normale ![]() .
.
Contrairement à la convergence d’une {suite} de variables aléatoires ![]() , la convergence d’une {série} de variables aléatoires
, la convergence d’une {série} de variables aléatoires ![]() ne dépend pas que des lois des variables
ne dépend pas que des lois des variables ![]() (
(![]() ) ; elle est liée à la loi de la somme partielle
) ; elle est liée à la loi de la somme partielle ![]() qui elle-même ne peut se déduire de la seule connaissance des lois des variables
qui elle-même ne peut se déduire de la seule connaissance des lois des variables ![]() (
(![]() ), sauf en cas d’indépendance.\\
), sauf en cas d’indépendance.\\
Or dans cet exemple les variables aléatoires ![]() (
(![]() ) sont indépendantes, mais les variables
) sont indépendantes, mais les variables ![]() (
(![]() ) ne le sont pas.\\
) ne le sont pas.\\
Précisément, pour tout ![]() , les variables
, les variables ![]() et
et ![]() ne sont pas indépendantes puisque :
ne sont pas indépendantes puisque :
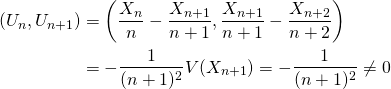
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie II : Séries harmoniques « lacunaires »
5/ a/ ![]()
b/ Comme ![]() (ce que l’on déduit de l’inégalité
(ce que l’on déduit de l’inégalité ![]() ):
):
![]()
c/ Si ![]() avec
avec ![]() , alors
, alors ![]() et
et ![]() .
.
Réciproquement, supposons que ![]() est à la fois un carré et un cube:
est à la fois un carré et un cube:
![]()
En posant ![]() (
(![]() ), on a :~
), on a :~ 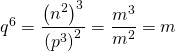 .\\
.\\
De plus, ![]() (car
(car ![]() ) donc
) donc ![]() est entier.\\
est entier.\\
Avec la propriété admise dans l’énoncé, comme ![]() n’est pas irrationnel et
n’est pas irrationnel et ![]() est entier,
est entier, ![]() est entier.
est entier.
d/ En distinguant chacun des quatre cas { \og ![]() et
et ![]() \fg{}}, {\og
\fg{}}, {\og ![]() et
et ![]() \fg{}}, { \og
\fg{}}, { \og ![]() et
et ![]() \fg{}} et {{purple}\og
\fg{}} et {{purple}\og ![]() et
et ![]() \fg{}}, on vérifie que :
\fg{}}, on vérifie que :
![]()
et on obtient alors, avec la même explication qu’en (a) :
![Rendered by QuickLaTeX.com \[h_n(\mathcal D\cup \mathcal T)=\sum_{\substack{k\in\{1,\dots,n\}\\ k\in\mathcal D}} \dfrac1k+\sum_{\substack{k\in\{1,\dots,n\}\\ k\in\mathcal T}} \dfrac1k-\sum_{\substack{k\in\{1,\dots,n\}\\ k\in\mathcal D\cap T}} \dfrac1k \tendinf{n} \zeta(2)+\zeta(3)-\zeta(6).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b52a9beb9ab5dd3bf0ee85bbd267c941_l3.png)
6/ a/ Pour tout ![]() :
:
![]()
On obtient donc l’encadrement demandé par croissance de l’intégrale.
b/
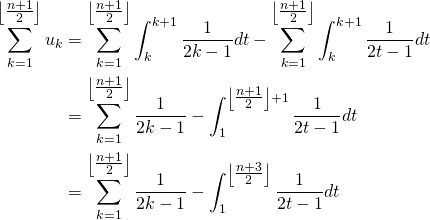
et donc :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{\left\lfloor\tfrac{n+1}2\right\rfloor} u_k +\int_1^{\left\lfloor\tfrac{n+3}2\right\rfloor}\dfrac1{2t-1}dt = \sum_{k=1}^{\left\lfloor\tfrac{n+1}2\right\rfloor}\dfrac1{2k-1} = \sum_{\substack{\ell\in\{1,\dots,n\}\\ \ell \text{ impair}}} \dfrac1\ell = h_n(\mathcal I).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c50e6ebe9168cd9f7195c7d9d749a509_l3.png)
En effet, ![]() est le plus grand entier impair inférieur ou égal à
est le plus grand entier impair inférieur ou égal à ![]() (il vaut
(il vaut ![]() si
si ![]() est pair ;
est pair ; ![]() si
si ![]() est impair) :
est impair) :
si ![]() (
(![]() ) :~
) :~ ![]() ;
;
si ![]() :~
:~ ![]() .
.
c/
![]()
{(que l’on retrouve par exemple en étudiant la fonction \og différence des deux membres \fg{})} donne :
![Rendered by QuickLaTeX.com \[\forall n\in\N^*,~ \ln\Bigg(\dfrac1n\left(2\left\lfloor \dfrac{n+3}2\right\rfloor-1\right)\Bigg) \leq \dfrac2n \underbrace{\left\lfloor \dfrac{n+3}2\right\rfloor}_{\geq 1}\overbrace{-\dfrac1n-1}^{\leq 0} \leq \dfrac2n.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6dde98f2852eff54c4e85760a794aafb_l3.png)
d/ La série ![]() est convergente car son terme général (positif) est équivalent à
est convergente car son terme général (positif) est équivalent à ![]() et la série de Riemann
et la série de Riemann ![]() converge.\\
converge.\\
L’encadrement établi en (a) donne donc la convergence de la série ![]() .\\
.\\
Avec l’égalité de la question (b):
![Rendered by QuickLaTeX.com \begin{align*}h_n(\mathcal I)-\ln(\sqrt n) &= \sum_{k=1}^{\left\lfloor\tfrac{n+1}2\right\rfloor}u_k + \int_1^{\left\lfloor \tfrac{n+3}2\right\rfloor} \dfrac1{2t-1}dt-\ln(\sqrt n)\\ &=\sum_{k=1}^{\left\lfloor\tfrac{n+1}2\right\rfloor}u_k + \left[\dfrac12\ln(2t-1)\right]_1^{\left\lfloor \tfrac{n+3}2\right\rfloor} -\ln(\sqrt n)\\ &=\sum_{k=1}^{\left\lfloor\tfrac{n+1}2\right\rfloor}u_k + \dfrac12\ln\Bigg(2\left\lfloor \dfrac{n+3}2\right\rfloor-1\Bigg) \underbrace{-\ln(\sqrt n)}_{=\tfrac12\ln\left(\tfrac1n\right)}\\ &=\underbrace{\sum_{k=1}^{\left\lfloor\tfrac{n+1}2\right\rfloor}u_k}_{\mathclap{\substack{\tendinf \xrightarrow n \delta\\ \text{car } \left\lfloor\tfrac{n+1}2\right\rfloor\mathop{\longrightarrow}\limits_{n\to+\infty} +\infty}}} ~~+~~ \underbrace{\dfrac12\ln\Bigg(\dfrac1n\left(2\left\lfloor \dfrac{n+3}2\right\rfloor-1\right)\Bigg)}_{\substack{\tendinf \xrightarrow n 0\text{ d'après (c) et}\\ \text{le théorème d'encadrement}}}~~\tendinf \xrightarrow n \delta. \end{align*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e646b3a9953d4fd4c464d68c6a3d85d3_l3.png)
e/ D’après la majoration de ![]() établie en question (a), il suffirait de prouver que :
établie en question (a), il suffirait de prouver que :
![Rendered by QuickLaTeX.com \[\forall n\in\N^*,~ \sum_{k=n+1}^{+\infty} \dfrac2{(2k-1)^2} \leq \dfrac1{2n-1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d06b5b45ce3cbaed917d4c1e44ada70d_l3.png)
On peut utiliser la technique suivante assez classique.\\
La fonction 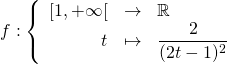 étant décroissante, on a :
étant décroissante, on a :
![]()
donc en sommant ces inégalités pour ![]() et avec la relation de Chasles:
et avec la relation de Chasles:
![Rendered by QuickLaTeX.com \[\sum_{k=n+1}^{+\infty} \dfrac2{(2k-1)^2} \leq \int_n^{+\infty} \dfrac2{(2t-1)^2} dt = \dfrac1{2n-1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b1fb6a66df84e017b095786a47ad5b10_l3.png)
f/ On utilise le calcul fait en question (d):
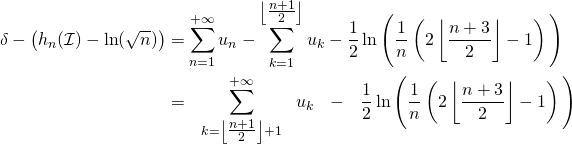
Cette dernière somme étant positive, la question (c) donne immédiatement :
![]()
De même {le logarithme dans l’égalité ci-dessus} étant positif, la question (e) donne:
![Rendered by QuickLaTeX.com \[\delta-\big(h_n(\mathcal I)-\ln(\sqrt n)\big) \leq ~~\sum_{\mathclap{k=\left\lfloor\tfrac{n+1}2\right\rfloor+1}}^{+\infty} ~~u_k~~ \leq \dfrac1{2\left\lfloor\dfrac{n+1}2\right\rfloor-1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-770039bdde5deaede75bfbe4dec4edc0_l3.png)
En utilisant l’inégalité ![]() , valable pour tout
, valable pour tout ![]() , on a:
, on a:
![Rendered by QuickLaTeX.com \[\dfrac1{2\left\lfloor\dfrac{n+1}2\right\rfloor-1} \leq \dfrac1{2\left(\dfrac{n+1}2-1\right)-1} = \dfrac1{n-2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f843ccdc3f188ea3976b302134cc3d72_l3.png)
et donc :
![]()
g/ On a :
![]()
Pour eps=0.2, le programme affectera à s successivement les valeurs de :
![]()
~~
function s=delta(eps)
n = 3
s = 1+1/3-log(3)/2
while 1/(n-2) > eps
n = n+2
s = s+1/n+log((n-2)/n)/2
end
endfunction
L’encadrement de la question (f) donne :
![]()
Il existe donc un entier ![]()
![]() ) tel que
) tel que ![]() , ce qui assure la précision souhaitée.
, ce qui assure la précision souhaitée.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie III : Séries de Riemann alternées
7/ a/
![]()
on a, pour tout ![]() :
:
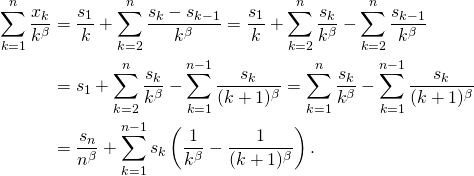
Prouvons la convergence (pour ![]() ) de chacun des deux termes ci-dessus :
) de chacun des deux termes ci-dessus :
![Rendered by QuickLaTeX.com \[\dfrac{s_n}{n^\beta} \quad\text{ et }\quad \sum_{k=1}^{n-1} s_k\left(\dfrac1{k^\beta}-\dfrac1{(k+1)^\beta}\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1f46a6f8f8e113da8991953fa06da992_l3.png)
Avec la majoration de ![]() supposée dans l’énoncé, on a:
supposée dans l’énoncé, on a:
![Rendered by QuickLaTeX.com \[\forall n\in\N^*,~ 0 \leq \left|\dfrac{s_n}{n^\beta}\right| \leq \underbrace{M n^{\alpha-\beta}}_{\substack{\tendinf \xrightarrow n 0\\\text{ car }\alpha-\beta<0}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cdcd0d80ee9412de0071bc8f9ddce327_l3.png)
donc par le théorème d’encadrement :
![]()
La question est donc de prouver la convergence de la série :
![]()
On va en montrer la convergence absolue (qui implique la convergence).\\
Avec l’hypothèse de l’énoncé sur ![]() :
:
![Rendered by QuickLaTeX.com \[\forall n\in\N^*,~ |s_n|\overbrace{\left(\dfrac1{n^\beta}-\dfrac1{(n+1)^\beta}\right)}^{(\geq 0)} \leq M~n^\alpha\left(\dfrac1{n^\beta}-\dfrac1{(n+1)^\beta}\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3aa9ee803714649e48dd08d65e104135_l3.png)
Déterminons un équivalent de ce majorant :
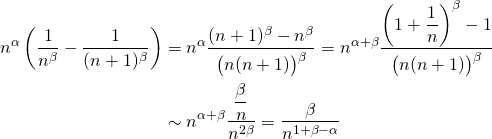
La série géométrique ![]() est convergente car
est convergente car ![]() (
(![]() ), donc par critères de comparaisons des séries à terme général positif, on obtient la convergence annoncée.
), donc par critères de comparaisons des séries à terme général positif, on obtient la convergence annoncée.
Conclusion : la série ![]() est convergente {(mais peut-être pas absolument!)}.
est convergente {(mais peut-être pas absolument!)}.
b/ En prenant ![]() , on a:
, on a:
![Rendered by QuickLaTeX.com \[\forall n\in\N^*,~ s_n=\sum_{k=1}^n x_k = -1+1-1+1-\dots(-1)^n= \left\{\begin{array}{c} 0\\\text{ou}\\-1\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f0d421c9710a4ef0df669b34d71e3a61_l3.png)
et en prenant ![]() et
et ![]() un réel vérifiant
un réel vérifiant ![]() (par exemple
(par exemple ![]() ):
):
![Rendered by QuickLaTeX.com \[\forall \in\N^*,~ |s_n| = \left\{\begin{array}{c} 0\\\text{ou}\\1\end{array}\right\} \leq \underbrace{M~n^\alpha}_{\substack{=1 \text{ pour }n=1\\ \geq 1 \text{ pour tout }n}}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0f601d1d0abbaa50183ece3dc26b22a0_l3.png)
On choisit bien sûr ![]() (
(![]() ), et la question précédente nous donne la convergence de la série
), et la question précédente nous donne la convergence de la série ![]() pour tout
pour tout ![]() .
.
8/ a/ Déterminons d’abord la loi de ![]() :
:
Comme ![]() est somme de
est somme de ![]() nombres valant chacun 1 ou
nombres valant chacun 1 ou ![]() :
:
![]()
{(Mais il ne s’agit pas d’une égalité ; en effet ![]() ne prend parmi les valeurs de cet intervalle que celles de même parité que
ne prend parmi les valeurs de cet intervalle que celles de même parité que ![]() .)}
.)}
Pour tout ![]() , la variable aléatoire
, la variable aléatoire ![]() suit la loi
suit la loi ![]() .\\
.\\
Les variables aléatoires ![]() (
(![]() ) étant indépendantes, la stabilité additive de la loi binomiale donne :
) étant indépendantes, la stabilité additive de la loi binomiale donne :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^n Y_k =\dfrac12 S_n+\dfrac n2\hookrightarrow \mathcal B\left(n,\dfrac12\right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d90a86a865435c6f1f213a729de283a1_l3.png)
c’est-à-dire :
![]()
Appliquons le théorème de transfert :
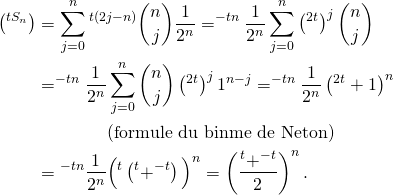
b/ Soit ![]() . Travaillons avec les sommes partielles des séries exponentielles intervenant ici ; pour
. Travaillons avec les sommes partielles des séries exponentielles intervenant ici ; pour ![]() :
:
![Rendered by QuickLaTeX.com \[\dfrac12\left(\sum_{k=0}^n \dfrac{t^k}{k!}+\sum_{k=0}^n \dfrac{(-t)^k}{k!}\right) =\overbrace{\dfrac12 \sum_{k=0}^n \dfrac{t^k+(-t)^k}{k!} = \sum_{\substack{k\in\{0,\dots,n\}\\ k\text{ pair}}} \dfrac{t^k}{k!}}^{\displaystyle t^k+(-t)^k=\left\{\begin{array}{cl}2t^k&\text{ si $k$ est pair}\\ 0&\text{sinon} \end{array}\right.} = \sum_{\ell=0}^{\left\lfloor \tfrac n2\right\rfloor} \dfrac{t^{2\ell}}{(2\ell)!}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6645c8478c10e42c470839d940dc0296_l3.png)
Or:~ ![]() ; en effet, il y a égalité pour
; en effet, il y a égalité pour ![]() , et pour
, et pour ![]() :
:
![Rendered by QuickLaTeX.com \[(2\ell)! = \ell!~\overbrace{\underbrace{(\ell+1)}_{\geq2}\dots\underbrace{(\ell+\ell)}_{\geq2}}^{\ell \text{ facteurs}}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-93972221656164c262519f5b2629693d_l3.png)
On a donc l’inégalité :
![Rendered by QuickLaTeX.com \[\dfrac12\left(\sum_{k=0}^n \dfrac{t^k}{k!}+\sum_{k=0}^n \dfrac{(-t)^k}{k!}\right) \leq \sum_{\ell=0}^{\left\lfloor \tfrac n2\right\rfloor} \dfrac{\left(t^2\right)^\ell}{2^\ell~ \ell!} = \sum_{\ell=0}^{\left\lfloor \tfrac n2\right\rfloor} \dfrac{\left(\dfrac{t^2}2\right)^\ell}{\ell!}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a611bc7da0349e6a13ee47e90da66b57_l3.png)
Par passage à la limite quand ![]() :
:
![]()
c/ Appliquons l’inégalité de Markov à la variable aléatoire positive ![]() :
:
![Rendered by QuickLaTeX.com \[\overbrace{\P(S_n>s) = \P\left(\e^{tS_n} > \e^{ts}\right) }^{\text{croissance de }\exp ~;~ t>0}\leq \underbrace{\dfrac{\E\left(\e^{tS_n}\right)}{\e^{ts}} \leq \dfrac{\left(\e^{\tfrac{t^2}2}\right)^n}{\e^{ts}}}_{\text{avec les questions (a) et (b)}}=\exp\left(\dfrac{nt^2}2-ts\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9c945d08458a56447791b88a2df46dd8_l3.png)
d/ L’inégalité prouvée en question précédente est vraie pour tout ![]() mais le membre de gauche ne dépend pas de
mais le membre de gauche ne dépend pas de ![]() . Or le membre de droite est minimal pour
. Or le membre de droite est minimal pour ![]() (il suffit de faire le tableau de variations de
(il suffit de faire le tableau de variations de ![]() ). Donc :
). Donc :
![Rendered by QuickLaTeX.com \[\P(S_n>s) \leq \exp\left(\dfrac{n{{\left(\dfrac sn\right)}}^2}2-{\left(\dfrac sn\right)}s\right) = \exp\left(-\dfrac{s^2}{2n}\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-caa67cca2bd52749d643695b3845c452_l3.png)
Par ailleurs :
![]()
et on vérifie que les deux probabilités ![]() et
et ![]() sont égales en utilisant la loi de
sont égales en utilisant la loi de ![]() déterminée en (a) :
déterminée en (a) :
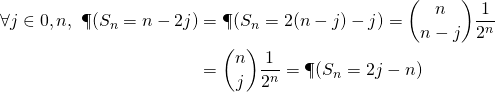
![]()
On conclut :
![]()
9/ a/ La stabilité d’une tribu par unions et intersections dénombrables justifie l’appartenance de ![]() à
à ![]() .
.
b/ Supposons ![]() . D’après 8.(d):
. D’après 8.(d):
![Rendered by QuickLaTeX.com \[\forall n\geq 1,~ \P(|S_n| > n^\alpha) \leq 2\exp\left(-\dfrac12n^{2\alpha-1}\right)=2\left(\dfrac1{\sqrt\e}\right)^{\displaystyle n^{2\alpha-1}}=2~q^{\displaystyle n^{\beta}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-416bb0bf9af78b7926bb36d645a916bc_l3.png)
avec ![]() et
et ![]() .
.
Par croissances comparées :
![Rendered by QuickLaTeX.com \[\dfrac{q^{\displaystyle n^{\beta}}}{n^2} = \left(\dfrac{q^n}{n^{\tfrac 2\beta}}\right)^\beta \tendinf \xrightarrow n 0.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b9f6d1f08baa2c8ab8ac9ba576737972_l3.png)
Par comparaison avec la série de Riemann convergente ![]() , la série à terme général positif
, la série à terme général positif ![]() est convergente et, avec l’inégalité ci-dessus, il en est donc de même de la série à terme général positif
est convergente et, avec l’inégalité ci-dessus, il en est donc de même de la série à terme général positif ![]() .
.
c/ La suite d’événements ![]() est décroissante :
est décroissante :
![Rendered by QuickLaTeX.com \[\forall n\geq1,~ \mathop{\bigcup}\limits_{k=n+1}^{+\infty} \big(|S_k|>k^\alpha\big) \subset \mathop{\bigcup}\limits_{k=n}^{+\infty} \big(|S_k|>k^\alpha\big).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b7ab4443b3676b42381c9ebdd0391e76_l3.png)
Le théorème de la limite monotone donne donc :
![Rendered by QuickLaTeX.com \[\P(C_\alpha)=\lim_{n\to+\infty} \P\left(\mathop{\bigcup}\limits_{k=n}^{+\infty} \big(|S_k|>k^\alpha\big)\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ab1b8ba09bb80d981b388ced90e60b27_l3.png)
De plus :
![Rendered by QuickLaTeX.com \[0\leq \P\left(\mathop{\bigcup}\limits_{k=n}^{+\infty} \big(|S_k|>k^\alpha\big)\right) \leq \underbrace{\sum_{k\geq n}\P\Big(\big(|S_k|>k^\alpha\big)\Big)}_{\substack{\tendinf \xrightarrow n0\\ \text{(reste d'une série convergente)}}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5dc00171d2739b588a79dcb7aa6e9322_l3.png)
et on conclut avec le théorème d’encadrement que ![]() est de probabilité nulle.
est de probabilité nulle.
10/ a/ Soit ![]() .\\
.\\
On remarque que :
![]()
Soit ![]() . Écrivons la négation de l’assertion précédente :
. Écrivons la négation de l’assertion précédente :
![]()
En posant, pour tout ![]() :
:
![]()
les hypothèses de la question 7. sont vérifiées.\\
On en déduit avec 7.(a)ii. la convergence de la série ![]() .\\ Autrement dit :~
.\\ Autrement dit :~ ![]() .
.
b/ Soit ![]() (par exemple
(par exemple ![]() ).\\
).\\
D’après la question 9., ![]() donc
donc ![]() .\\
.\\
Donc avec l’inclusion prouvée en question 10.(a) et par croissance de ![]() :~
:~ ![]() .
.
c/ Si ![]() , par définition de
, par définition de ![]() , on a
, on a ![]() c’est-à-dire:
c’est-à-dire:
![]()
Or par définition de ![]() :
:
![]()
ce qui est exactement la négation de l’assertion précédente.\\
Par conséquent :
![]()
et on en déduit :
![]()
Comme pour la question 9.(c), le théorème de la limite monotone donne :
![Rendered by QuickLaTeX.com \[\lim_{N\to+\infty} \P\left(\mathop{\bigcup}\limits_{n=N}^{+\infty} \big(|K-K_n|>\varepsilon\big)\right)=\P\big(E(\varepsilon)\big)=0.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3a9c4e113c1584edf173c20bcc1c26d5_l3.png)
En écrivant, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[0\leq \P\big(|K-K_N|>\varepsilon\big) \leq \P\left(\mathop{\bigcup}\limits_{n=N}^{+\infty} \big(|K-K_n|>\varepsilon\big)\right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-66b5a4a2802932ffe9332cd97ba7d8ab_l3.png)
le théorème d’encadrement donne :
![]()
ce qui signifie que la suite de variable aléatoire ![]() converge en probabilité vers
converge en probabilité vers ![]() .
.
11/ a/ Pour tout ![]() , la variable
, la variable ![]() est d’espérance
est d’espérance ![]() et de variance
et de variance ![]() .\\
.\\
Par linéarité de l’espérance et propriété de la variance (utilisant l’indépendance des variables ![]() (
(![]() )):
)):
![Rendered by QuickLaTeX.com \[\E(H_n)=\sum_{k=1}^n\dfrac1{2k} \tendinf \xrightarrow n +\infty \quad ; \quad \V(H_n)=\sum_{k=1}^n \dfrac1{4k^2} \tendinf \xrightarrow n \dfrac{\zeta(2)}4=\dfrac{\pi^2}{24}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9c496e53043d125de43a2cdf4319d55a_l3.png)
b/ Soit ![]() . Comme
. Comme ![]() :
:
![]()
On peut alors utiliser l’inégalité de Bienaymé-Tchébychev :
![]()
ce qui donne :
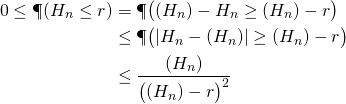
Avec les deux limites trouvées en (a) :
![]()
On conclut avec le théorème d’encadrement que :
![]()
c/ On peut proposer le programme suivant :
function y=simul (n,p)
y=zeros (p,1)
for i=1 : p
for k=1 : n
y (i,1) = y(i,1)+ (grand (i,1,’bin’,1,0.5) + ((-1)^k-1)/2) /k
end
end
endfunction
12/ Pour tout ![]() , :
, :
![Rendered by QuickLaTeX.com \[\hspace{-1cm}\sum_{k=1}^n \dfrac{B_k^\prime}k-h_n(\mathcal I) = \sum_{k=1}^n \dfrac{1+X_k}{2k}+\sum_{k=1}^n \dfrac{(-1)^k-1}{2k} = \dfrac12 \sum_{k=1}^n \dfrac{X_k}k + \sum_{k=1}^n \dfrac{(-1)^k}{2k} = \dfrac{K_n}2 + \sum_{k=1}^n \dfrac{(-1)^k}{2k}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-bdd4121e06f123505dd46e224c3a0d92_l3.png)
Les variables aléatoires ![]() (
(![]() ) suivent la loi de Bernoulli de paramètre
) suivent la loi de Bernoulli de paramètre ![]() {(astuce utilisée en question 8.(a))}, c’est-à-dire la même loi que
{(astuce utilisée en question 8.(a))}, c’est-à-dire la même loi que ![]() , et sont indépendantes (car les
, et sont indépendantes (car les ![]() le sont).\\
le sont).\\
Les lois des variables ![]() et
et ![]() sont donc les mêmes.
sont donc les mêmes.
La convergence en loi de ![]() vers
vers ![]() et le théorème de Slutsky donnent donc :
et le théorème de Slutsky donnent donc :
![Rendered by QuickLaTeX.com \[H_n-h_n(\mathcal I) \xrightarrow[]{~~\mathcal L~~} \dfrac K2+\dfrac12\sum_{n=1}^{+\infty} \dfrac{(-1)^n}n\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ac07523373ec4632b340b942075eba9c_l3.png)
Cette somme vaut ![]() ; en effet : pour tout réel
; en effet : pour tout réel ![]() , la série
, la série ![]() converge de somme
converge de somme ![]() .\\
.\\
On a donc :
![]()

