Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet ECRICOME Maths ECS 2018
Revenir à tous les corrigés des annales maths Ecricome
Exercice 1 : Caractérisation d’un projecteur
Partie 1 :
1/ On montre que ![]() et
et ![]() Pour cela on utilise l’interprétation matricielle des endomorphismes dans la base
Pour cela on utilise l’interprétation matricielle des endomorphismes dans la base ![]() .
.
![]()
![]()
Donc ![]() et
et
![]()
De façon analogue, on a ![]() donc
donc ![]() donc
donc ![]() et
et
![]()
2/ a/ On sait que ![]() Or la deuxième colonne de
Or la deuxième colonne de ![]() est égale à la première multipliée par
est égale à la première multipliée par ![]() donc le rang de
donc le rang de ![]() est
est ![]() car il s’agit d’une colonne non nulle.
car il s’agit d’une colonne non nulle.
Le rang de ![]() est celui de
est celui de ![]() , il est immédiat que le rang de
, il est immédiat que le rang de ![]() est 1 car les colonnes de
est 1 car les colonnes de ![]() sont non nulles et égales.
sont non nulles et égales.
Enfin ![]() après calculs. Là aussi, il y a des colonnes qui sont non nulles et égales. Donc
après calculs. Là aussi, il y a des colonnes qui sont non nulles et égales. Donc ![]() est aussi de rang 1.
est aussi de rang 1.
Bilan :
![]()
b/ On sait que ![]()
Ainsi
![]()
Donc ![]() . Remarquons que
. Remarquons que ![]()
Bilan :
![]()
c/ On sait que ![]() est de rang 1 et que
est de rang 1 et que ![]() est de dimension 2 donc
est de dimension 2 donc ![]() n’est pas bijectif donc 0 est valeur propre de
n’est pas bijectif donc 0 est valeur propre de ![]() .
.
On pense alors à résoudre ![]()
ce qui est équivalent à ![]()
3/ a/ Si ![]() alors
alors ![]() comme
comme ![]() est de dimension 2, il y a au plus deux valeurs propres. Donc nous les avons toutes déterminées.
est de dimension 2, il y a au plus deux valeurs propres. Donc nous les avons toutes déterminées.
Si ![]() alors
alors ![]() et
et ![]() et
et ![]() . Dans ce cas, le spectre est réduit à 0.
. Dans ce cas, le spectre est réduit à 0.
Remarque : il est immédiat que, dans les deux cas, ![]() est vecteur propre de
est vecteur propre de ![]() associé à 0.
associé à 0.
Bilan :
![Rendered by QuickLaTeX.com \[\boxed { \text{Le spectre de $u\circ v$ est $\left\{0,\frac{1+2a+a^2}{2(1+a^2)}\right\}$ si $a\ne -1$ et il vaut $\left\{0\right\}$ si $a=-1$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-44e12f3322206fef6bb0b1817cd3de2d_l3.png)
Si ![]() la réponse est immédiate.
la réponse est immédiate.
Si ![]() , alors il faut juste s’assurer que
, alors il faut juste s’assurer que ![]()
Il est clair que le calcul de la fraction est positif car des réels au carré le sont.
Calculons ![]() .
.
Donc ![]()
Bilan :
![]()
b/ Supposons que ![]() est un projecteur. Si
est un projecteur. Si ![]() , alors
, alors ![]() est la fonction nulle, c’est donc le projecteur sur
est la fonction nulle, c’est donc le projecteur sur ![]() parallèlement à
parallèlement à ![]()
Si ![]() , alors le spectre de
, alors le spectre de ![]() contient deux valeurs, il ne peut s’agir que de 0 et 1. Car tout projecteur a pour polyn\^ome annulateur
contient deux valeurs, il ne peut s’agir que de 0 et 1. Car tout projecteur a pour polyn\^ome annulateur ![]() de racines
de racines ![]() et
et ![]()
On en déduit que ![]() par conséquent
par conséquent
![]() donc
donc ![]() donc
donc ![]() donc
donc ![]()
Réciproquement si ![]() alors
alors ![]() donc
donc ![]() donc
donc ![]() et
et ![]() est un projecteur,
est un projecteur, ![]() l’est aussi.
l’est aussi.
Bilan :
![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie 2 : Matrice symétrique et valeurs propres
4/ On va utiliser la symétrie de ![]() sous la forme
sous la forme ![]() puis le fait que
puis le fait que ![]() car
car ![]() est un projecteur symétrique dont
est un projecteur symétrique dont ![]() est sa matrice dans la base canonique.
est sa matrice dans la base canonique.
Pour tout ![]() , on a
, on a
![]()
Bilan : pour tout ![]() :
:
![]()
On utilise l’inégalité de Cauchy-Schwarz pour écrire
![]()
Si ![]() alors on a bien
alors on a bien ![]()
Sinon on peut diviser par ![]() et on obtient
et on obtient
![]()
5/ On montre que ![]() est symétrique en remarquant
est symétrique en remarquant
![]()
En effet on a ![]() car
car ![]() est symétrique et
est symétrique et ![]() est sa matrice dans la base canonique.
est sa matrice dans la base canonique.
De plus ![]() est à coefficients réels.
est à coefficients réels.
Bilan :
![]()
6/ Soit ![]() une valeur propre de
une valeur propre de ![]() et un
et un ![]() un vecteur propre associé par conséquent
un vecteur propre associé par conséquent ![]() n’est pas la colonne nulle.
n’est pas la colonne nulle.
a/ On a
![]()
![]()
Bilan :
![]()
b/ Comme ![]() n’est pas nulle, on peut diviser par
n’est pas nulle, on peut diviser par ![]() De sorte que
De sorte que ![]()
Bilan :
![]()
7/ Soit ![]() une (éventuelle) valeur propre de
une (éventuelle) valeur propre de ![]() non nulle, et
non nulle, et ![]() un vecteur propre associé. On a donc
un vecteur propre associé. On a donc ![]()
a/ Dans un premier temps remarquons que ![]() car
car ![]() et
et ![]() sont non nuls. Par conséquent
sont non nuls. Par conséquent ![]() n’est pas la colonne nulle sinon
n’est pas la colonne nulle sinon ![]() serait nulle. Calculons
serait nulle. Calculons
![]()
Bilan :
![]()
b/ On a ![]() .
.
Or ![]() donc
donc ![]() . Comme
. Comme ![]() est non nul, on peut diviser par
est non nul, on peut diviser par ![]()
Bilan :
![]()
c/ On utilise ce qui précède
![]()
Bilan :
![]()
8/ Une éventuelle valeur propre nulle est bien dans ![]()
Soit ![]() une valeur propre non nulle de
une valeur propre non nulle de ![]() et
et ![]() un vecteur propre associé, avec la question 4., on a
un vecteur propre associé, avec la question 4., on a ![]() .
.
La question 7.c), donne ![]() donc
donc ![]() .
.
On utilise encore la question 4., cela donne ![]()
On divise par ![]() , on a alors
, on a alors ![]()
Donc ![]()
Bilan :
![]()
Exercice 2 : Théorème de Schwarz
1/ On utilise la stricte croissance de la racine carrée sur ![]()
![]()
Le discriminant de ![]() est
est ![]() On a alors deux racines réelles distinctes
On a alors deux racines réelles distinctes ![]() et
et ![]()
Or ![]()
Bilan :
![Rendered by QuickLaTeX.com \[\boxed { \text{$\varphi>1$ et les r\'eels $\varphi$ et $\frac{-1}{\varphi}$ sont les solutions de l'\'equation : $x^{2}-x-1=0$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-00aa9dce19ad127ffbef59680c298aa7_l3.png)
2/ a/ ![]() est de classe
est de classe ![]() sur
sur ![]() comme fonction de type polynomial en
comme fonction de type polynomial en ![]() et
et ![]() .
.
b/ ![]() étant de classe
étant de classe ![]() sur l’ouvert
sur l’ouvert ![]() les points critiques de
les points critiques de ![]() sont les solutions de
sont les solutions de ![]()
On calcule ![]() et
et ![]()
Ainsi ![]()
![]()
![]()
![]()
![]()
![]()
Or ![]() .
.
Et ![]()
Bilan : Les seuls points critiques de ![]() sont
sont ![]() et
et ![]() .
.
c/ On calcule la hessienne de ![]() , on a
, on a ![]() On a utilisé le théorème de Schwarz sachant
On a utilisé le théorème de Schwarz sachant ![]() de classe
de classe ![]()
![]()
La matrice est symétrique réelle, elle est diagonalisable dans ![]() On cherche les signes de ses valeurs propres lorsque
On cherche les signes de ses valeurs propres lorsque ![]() est un point critique. On peut étudier le spectre de
est un point critique. On peut étudier le spectre de ![]() car le spectre de
car le spectre de ![]() s’obtient en multipliant par 6 les valeurs propres de
s’obtient en multipliant par 6 les valeurs propres de ![]() .
.
On sait par ailleurs que ![]() est valeur propre de
est valeur propre de ![]() si et seulement si
si et seulement si ![]() est non inversible si et seulement si
est non inversible si et seulement si ![]()
On résout ![]()
On voit ![]() En effet les deux points critiques ont pour abscisses les racines de
En effet les deux points critiques ont pour abscisses les racines de ![]() donc dans les cas
donc dans les cas ![]()
Les racines sont donc ![]() et
et ![]()
Donc le spectre de ![]() est
est ![]() dans le cas où
dans le cas où ![]() est un point critique.
est un point critique.
Si ![]() , alors
, alors ![]() et
et ![]() sont strictement positifs donc
sont strictement positifs donc ![]() a un minimum local en
a un minimum local en ![]()
Si ![]() , alors
, alors ![]() et
et ![]() donc
donc ![]() n’a pas d’extremum en
n’a pas d’extremum en ![]() Il s’agit d’un point col.
Il s’agit d’un point col.
3/ On pose, pour tout entier ![]() ,
, ![]() .
.
Au rang 0, on a ![]() donc
donc ![]() Donc
Donc ![]() est vraie.
est vraie.
Supposons ![]() vraie pour un
vraie pour un ![]() alors
alors
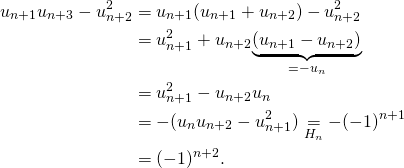
Donc
Bilan :
![]()
4/ a/
function u=suite(n)
v=0
w=1
for k=2:n // ici v vaut u(k-2) et w vaut u(k-1)
temporaire = v+w // temporaire vaut u(k-2) + u(k-1) = u(k)
v = w // v vaut u(k-1)
w = temporaire // w vaut u(k)
end // en sortie de boucle k=n et w vaut u(n)
u= w
endfunction
b/ On commence par résoudre
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l}\lambda\varphi^{0}+\mu\left(\frac{-1}{\varphi}\right)^{0} = u_0\\\lambda\varphi^{1}+\mu\left(\frac{-1}{\varphi}\right)^{1}=u_1\end{array}\right.\Longleftrightarrow \left\{\begin{array}{l}\lambda+\mu = 0\\\lambda\varphi+\mu\left(\frac{-1}{\varphi}\right)=1\end{array}\right. \Longleftrightarrow \left\{\begin{array}{l}\mu = - \lambda\\\lambda\left(\varphi+\left(\frac{1}{\varphi}\right)\right)=1\end{array}\right. \Longleftrightarrow \left\{\begin{array}{l}\mu = - \frac{\varphi}{\varphi^2+1}\\\lambda=\frac{\varphi}{\varphi^2+1}\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-676e47ab6fd948cb25452c61143d3896_l3.png)
On garde ces deux valeurs pour ![]() et
et ![]()
On pose ensuite :
![]()
Ce qui précède dit que ![]()
Il ne reste plus qu’à vérifier que la suite ![]() vérifie la même relation que
vérifie la même relation que ![]() , une récurrence double immédiate assurera que les deux suites sont égales.
, une récurrence double immédiate assurera que les deux suites sont égales.
Soit ![]()
![]()
![]()
Bilan :
![Rendered by QuickLaTeX.com \[\boxed { \text{$\forall n\in\mathbb{N},\quad u_{n}=\lambda\varphi^{n}+\mu\left(\frac{-1}{\varphi}\right)^{n}.$}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-84f7ed080b4b3d06b2f65b70c0fb29b6_l3.png)
c/ La suite ![]() a du sens car la suite
a du sens car la suite ![]() est non nulle à partir du rang 1. En effet, pour
est non nulle à partir du rang 1. En effet, pour ![]()
![]() On peut montrer facilement par récurrence double que
On peut montrer facilement par récurrence double que ![]() dès que
dès que ![]() La suite est strictement croissante à partir du rang 1 et
La suite est strictement croissante à partir du rang 1 et ![]()
On a 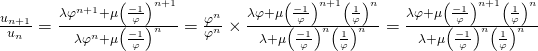
Il est clair que ![]() donc on peut diviser par
donc on peut diviser par ![]() , ainsi
, ainsi
![Rendered by QuickLaTeX.com \[\frac{u_{n+1}}{u_{n}}=\frac{\varphi+\frac{\mu}{\lambda}\left(\frac{-1}{\varphi}\right)^{n+1}\left(\frac{1}{\varphi}\right)^{n}}{1+\frac{\mu}{\lambda}\left(\frac{-1}{\varphi}\right)^{n}\left(\frac{1}{\varphi}\right)^{n}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0a6a85ffb894e85156315f468260d6ed_l3.png)
Or ![]() donc
donc ![]() donc
donc ![]()
Donc
![]()
5/ On considère pour tout ![]() :
: ![]()
a/ On montre d’abord que ![]() Pour cela on établit que le quotient converge vers 1.
Pour cela on établit que le quotient converge vers 1.
![]()
Ainsi on a ![]()
Or ![]() donc
donc ![]() donc
donc ![]() donc la série géométrique
donc la série géométrique ![]() converge.
converge.
Donc par comparaison des séries à terme général positif, la série de terme général ![]() converge.
converge.
b/ La série ![]() converge or
converge or ![]() donc la série
donc la série ![]() est absolument convergente donc convergente donc la suite
est absolument convergente donc convergente donc la suite ![]() de ses sommes partielles converge.
de ses sommes partielles converge.
c/ Pour tout ![]() :
:
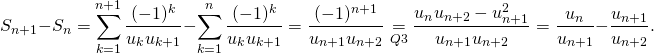
d/ Soit ![]() on somme ce qui précède de
on somme ce qui précède de ![]() à
à ![]() puis on réalise deux télescopages. Il est immédiat que
puis on réalise deux télescopages. Il est immédiat que ![]() , ces valeurs sont utilisées en fin de calcul.
, ces valeurs sont utilisées en fin de calcul.
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{N} \left( S_{n+1}-S_{n} \right)= \sum_{n=1}^{N} \left(\frac{u_{n}}{u_{n+1}}-\frac{u_{n+1}}{u_{n+2}}\right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b85f075a880643478e3b69bddd4e1e06_l3.png)
donc
![]()
donc
![]()
Donc
La question 4.c) a montré que ![]() Donc
Donc ![]()
Par conséquent, un passage à la limite dans la relation ![]() lorsque
lorsque ![]() indique que
indique que
![Rendered by QuickLaTeX.com \[\frac{1}{\varphi}=-\disp\sum_{k=1}^{+\infty}\frac{(-1)^{k}}{u_{k}u_{k+1}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-99f3af35d9931eda14c8c42e7cadc551_l3.png)
Pour conclure, il reste à établir que ![]()
En effet
![]()
Bilan :
![Rendered by QuickLaTeX.com \[\boxed { \text{$\varphi=1-\disp\sum_{k=1}^{+\infty}\frac{(-1)^{k}}{u_{k}u_{k+1}}$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-88076e1ce03074dd95cc9f5d49692c14_l3.png)
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Problème : Relation de Panjer
Partie 1 : Variables vérifiant une relation de Panjer
1/ a/ On a pour tout ![]() ,
, ![]() .
.
Montrons alors par récurrence que pour tout ![]() , la propriété
, la propriété ![]() : »
: » ![]() \fg\ est vraie. «
\fg\ est vraie. «
![]() , donc
, donc ![]() est vraie.
est vraie.
Soit ![]() . On suppose que
. On suppose que ![]() est vraie. Montrons que
est vraie. Montrons que ![]() est vraie.
est vraie.
![]()
La propriété est donc vraie au rang
Par axiome de récurrence, on en déduit que
![Rendered by QuickLaTeX.com \[\boxed { \text{$\forall k\in\mathbb{N} \qquad P(N=k)=\frac{b^k}{k!}P(N=0)$.}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f91782d076b809cb4e94276caa0af9e6_l3.png)
b/ La série de terme général ![]() est le multiple d’une série exponentielle. On en déduit qu’elle converge et on a
est le multiple d’une série exponentielle. On en déduit qu’elle converge et on a
![Rendered by QuickLaTeX.com \[\dis \sum_{k=0}^{+\infty}\frac{b^k}{k!}P(N=0)=P(N=0)\text{e}^{b}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d80648d942d50ee1eb07b1b99c8e650e_l3.png)
Or, la série de terme général ![]() coincide avec la série de terme général
coincide avec la série de terme général ![]() . Sa somme vaut donc aussi 1, car la famille
. Sa somme vaut donc aussi 1, car la famille ![]() est un système complet d’événements. On en déduit que
est un système complet d’événements. On en déduit que ![]() . Dès lors,
. Dès lors,
![]()
La variable aléatoire suit donc une loi de Poisson de paramètre ![]() . Par conséquent, elle admet une espérance et une variance égale à
. Par conséquent, elle admet une espérance et une variance égale à ![]() et
et ![]() .
.
2/ a/ Montrons par une récurrence rapide que pour tout ![]() ,
, ![]() .
.
![]() .
.
Soit ![]() . Supposons que
. Supposons que ![]() . Montrons que
. Montrons que ![]() .
.
![]()
par hypothèse de récurrence.
Par principe de récurrence, on a bien
![]()
b/ On déduit de la question précédente que ![]() . Par conséquent,
. Par conséquent, ![]() suit une loi de Bernouilli. De plus,
suit une loi de Bernouilli. De plus,
![]()
D’où, ![]() et comme
et comme ![]() ,
, ![]() . Par conséquent,
. Par conséquent,
![]() suit une loi de Bernoulli de paramètre
suit une loi de Bernoulli de paramètre ![]() .
.
3/ a/ Soit ![]() .
. ![]() . Or
. Or ![]() . D’où
. D’où
![]()
b/ On a déjà comme ![]() que
que ![]() . De plus, avec la relation précédente, en posant
. De plus, avec la relation précédente, en posant ![]() et
et ![]() , on a bien
, on a bien ![]() car
car ![]() et
et ![]() et
et
![]()
Enfin, ![]() . La relation précédente reste donc vraie pour
. La relation précédente reste donc vraie pour ![]() et par une récurrence immédiate du même type que celle effectuée à la question 2.a, elle reste vraie pour
et par une récurrence immédiate du même type que celle effectuée à la question 2.a, elle reste vraie pour ![]() car tous les termes sont nuls. On a donc bien
car tous les termes sont nuls. On a donc bien
![]()
La variable aléatoire ![]() vérifie donc une relation de Panjer.
vérifie donc une relation de Panjer.
4/ a/ ![]() .
.
Raisonnons par l’absurde et supposons ![]() . Alors, une récurrence immédiate du type de celle de la question 2.a montre que pour tout
. Alors, une récurrence immédiate du type de celle de la question 2.a montre que pour tout ![]()
![]() , ce qui est exclu. On en déduit que
, ce qui est exclu. On en déduit que ![]() . Or
. Or ![]() d’où
d’où
![]()
b/ Soit ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}\displaystyle \sum_{k=1}^{m}kP(N=k)&=&{\dis a\sum_{k=1}^mkP(N=k-1)+b\sum_{k=1}^{m}P(N=k-1)}\\&=&{\dis a\sum_{j=0}^{m-1}(j+1)P(N=j)+b\sum_{j=0}^{m-1}P(N=j)}\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f7f05c6ec28247597fd7ebc687d637a9_l3.png)
en faisant les changements de variables ![]() dans les deux sommes.
dans les deux sommes.
c/ Avec le résultat de la question précédente, on a donc pour tout ![]()
![Rendered by QuickLaTeX.com \[\dis (1-a)\sum_{k=1}^{m-1}kP(N=k)+mP(N=m)=(a+b)\sum_{k=0}^{m-1}P(N=k)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7cb0a3232feb5cf38ab3e6225357d864_l3.png)
D’où pour tout ![]() ,
,
![Rendered by QuickLaTeX.com \[\dis (1-a)\sum_{k=1}^{m}kP(N=k)+(m+1)P(N=m+1)=(a+b)\sum_{k=0}^{m}P(N=k)\qquad (\ast)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-798613e17e1fb53ba70dde2410c23bd6_l3.png)
Or, ![]() ,
, ![]() ,
, ![]() et
et ![]() . Dès lors,
. Dès lors,
![Rendered by QuickLaTeX.com \[\dis (1-a)\sum_{k=1}^{m}kP(N=k)\leq a+b \qquad \text{et} \qquad \dis \sum_{k=1}^{m}kP(N=k)\leq \frac{a+b}{1-a}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1c525ff029f3188c66eb5df895c0af49_l3.png)
La suite ![]() est donc majorée par
est donc majorée par ![]() .
.
De plus, la suite ![]() est croissante majorée par
est croissante majorée par ![]() . Par théorème de convergence monotone, elle converge.
. Par théorème de convergence monotone, elle converge.
La variable aléatoire ![]() admet une espérance si et seulement si la série de terme général
admet une espérance si et seulement si la série de terme général ![]() est absolument convergente ce qui équivaut ici à sa convergence car la variable aléatoire
est absolument convergente ce qui équivaut ici à sa convergence car la variable aléatoire ![]() est à valeurs dans
est à valeurs dans ![]() .
.
On en déduit donc que
![]()
Par conséquent, ![]() comme terme général d’une série convergente. Comme
comme terme général d’une série convergente. Comme ![]() , en faisant tendre
, en faisant tendre ![]() vers
vers ![]() dans la relation
dans la relation ![]() , on en déduit que
, on en déduit que
![]()
d/ On raisonne avec des calculs similaires à ceux menés dans la question 4.
On a alors pour tout ![]() ,
,
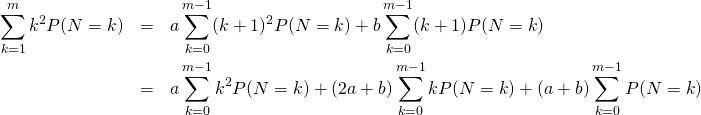
On a ainsi
![Rendered by QuickLaTeX.com \[{\dis (1-a)\sum_{k=1}^{m-1}k^2P(N=k)+m^2P(N=m)=(2a+b)\sum_{k=0}^{m-1}kP(N=k)+(a+b)\sum_{k=0}^{m-1}P(N=k)}\qquad\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1d3866693415994bb872ab3b8fbec956_l3.png)
On a déjà montré que ![]() .
.
Il reste à montrer que ![]() . On a
. On a ![]() .
.
Si ![]() , alors par une récurrence immédiate, on montre que pour tout
, alors par une récurrence immédiate, on montre que pour tout ![]() ,
, ![]() d’où
d’où ![]() , ce qui est exclu.
, ce qui est exclu.
On a donc ![]() et en fait même
et en fait même ![]() . Comme
. Comme ![]() , on en déduit que
, on en déduit que ![]() . Dès lors, pour tout
. Dès lors, pour tout ![]() , en appliquant la dernière égalité au rang
, en appliquant la dernière égalité au rang ![]() , il vient comme
, il vient comme ![]() ,
,
![Rendered by QuickLaTeX.com \[{\dis (1-a)\sum_{k=1}^mk^2P(N=k)\leq (2a+b)E(N)+(a+b)}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-89b7309d33de4cfaa79a0cc56ee66f92_l3.png)
car ![]() et
et ![]() . Ainsi,
. Ainsi, ![]() .
.
La suite ![]() est donc croissante majorée. Par théorème de convergence monotone, elle converge.
est donc croissante majorée. Par théorème de convergence monotone, elle converge.
La série de terme général ![]() est donc absolument convergente car convergente à termes positifs et
est donc absolument convergente car convergente à termes positifs et ![]() admet un moment d’ordre 2. De plus,
admet un moment d’ordre 2. De plus, ![]() . En faisant tendre
. En faisant tendre ![]() vers
vers ![]() dans l’égalité
dans l’égalité ![]() , on obtient
, on obtient
![]()
e/ La variable aléatoire ![]() admet un moment d’ordre 2 donc une variance. Avec la formule de Koenig-Huygens, il vient
admet un moment d’ordre 2 donc une variance. Avec la formule de Koenig-Huygens, il vient
![]()
f/ On a déjà que si ![]() suit une loi de Poisson alors
suit une loi de Poisson alors ![]() .
.
Réciproquement, supposons ![]() . Avec les résultats des question 4.c et 4.d, on a alors
. Avec les résultats des question 4.c et 4.d, on a alors
![]() ou
ou ![]()
Si ![]() , alors
, alors ![]() et par une récurrence immédiate, on en déduit que
et par une récurrence immédiate, on en déduit que ![]() pour tout
pour tout ![]() . D’où
. D’où ![]() ce qui est exclu.
ce qui est exclu.
On en déduit que ![]() d’où
d’où ![]() . D’après la question 1.b, on en déduit que
. D’après la question 1.b, on en déduit que ![]() suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre ![]() .
.
On a donc bien l’équivalence voulue.
Partie 2 : Fonction génératrice
5/ Soit ![]() . Pour tout
. Pour tout ![]() ,
, ![]() . La série de terme général
. La série de terme général ![]() est convergente de somme
est convergente de somme ![]() donc par théorème de comparaison pour les séries à termes positifs, la série de terme général
donc par théorème de comparaison pour les séries à termes positifs, la série de terme général ![]() converge.
converge.
6/ Soit ![]() ,
, ![]() car
car ![]() et
et ![]() . Par composition, la fonction
. Par composition, la fonction ![]() est donc de classe
est donc de classe ![]() sur
sur ![]() .
.
Montrons par récurrence que pour tout ![]() , la propriété
, la propriété ![]() : »
: » ![]() ,
, ![]() . »
. »
![]() Pour tout
Pour tout ![]() ,
, ![]() . Donc
. Donc ![]() est vraie.
est vraie.
![]() Soit
Soit ![]() . On suppose
. On suppose ![]() vraie. Montrons que
vraie. Montrons que ![]() est vraie.
est vraie.
Par hypothèse de récurrence, pour tout ![]() ,
, ![]() . Alors, pour tout
. Alors, pour tout ![]() ,
,
![]()
Or, ![]() et
et ![]() . On en déduit que
. On en déduit que
![]()
et ![]() est vraie.
est vraie.
Par axiome de récurrence, la propriété ![]() est vraie pour tout
est vraie pour tout ![]() .
.
7/ Soit ![]() .
.
a/ Soit ![]() . La fonction
. La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() donc par théorème de Taylor avec reste intégral à l’ordre
donc par théorème de Taylor avec reste intégral à l’ordre ![]() appliqué entre
appliqué entre ![]() et
et ![]() , on a
, on a
![Rendered by QuickLaTeX.com \[f(x)=\dis \sum_{k=0}^{n}\frac{f^{(k)}(0)}{k!}x^k+\int_{0}^{x}\frac{(x-t)^n}{n!}f^{(n+1)}(t)\text{d} t\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-21581f06c6eb533afa54025286f28738_l3.png)
D’où, avec les résultats de la question précédente,
![Rendered by QuickLaTeX.com \[f(x)=\dis \sum_{k=0}^{n}p_kx^k+(n+1)p_{n+1}\int_{0}^{x}(x-t)^n(1-at)^{\alpha-(n+1)}\text{d} t\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-71de53f10fc67bb1b852b8412dd56b71_l3.png)
b/ Soit ![]() .
.
![]()
Or,
![]()
car ![]() . Par croissance de l’intégrale, il vient
. Par croissance de l’intégrale, il vient
![]()
c/ Avec la question précédente, on a pour tout ![]() ,
,
![]()
Or,
![]()
Avec l’égalité de la question 7.a, en faisant tendre ![]() vers
vers ![]() , on obtient
, on obtient
![]() d’où
d’où ![]() .
.
![]() . De plus,
. De plus, ![]() . Par conséquent,
. Par conséquent, ![]() .
.
En outre, pour tout ![]() ,
, ![]() . D’où
. D’où ![]() . Ainsi par définition de
. Ainsi par définition de ![]() ,
,
![]()
Partie 3 : Formule de récursivité
9/ La famille ![]() est un système complet d’événements. Par conséquent, d’après la formule des probabilités totales,
est un système complet d’événements. Par conséquent, d’après la formule des probabilités totales,
![Rendered by QuickLaTeX.com \[P(S=0)=\dis \sum_{k=0}^{+\infty} P((S=0)\cap [N=k])\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8bb5aab6ab327976f04190d9457adf39_l3.png)
![]() et si
et si ![]() , les variables aléatoires
, les variables aléatoires ![]() étant à valeurs dans
étant à valeurs dans ![]() ,
,
![Rendered by QuickLaTeX.com \[(S=0)\cap [N=k]=\dis \bigcap_{i=1}^{k}[X_i=0]\cap [N=k]\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-00e2531a75386b2bf19800577cbd719e_l3.png)
Par mutuelle indépendance des variables aléatoires considérées, on a donc
![]()
car les variables aléatoires
En posant ![]() , il vient en utilisant les mêmes notations que celles de la partie 2 et les résultats de cette partie car
, il vient en utilisant les mêmes notations que celles de la partie 2 et les résultats de cette partie car ![]() (seule condition utile dans cette partie),
(seule condition utile dans cette partie),
![Rendered by QuickLaTeX.com \[P(S=0)=\dis \sum_{k=0}^{+\infty}p_k x^k=G(x)=\left(\frac{1-ax}{1-a}\right)^{\alpha}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-710ab3c5ef246c301f4fcc9f44506f34_l3.png)
10/ a/ Les calculs intermédiaires et le raisonnement de la question précédente restent vrais dans cette question. On a donc en posant ![]()
![Rendered by QuickLaTeX.com \[P(S=0)=\dis \sum_{k=0}^{+\infty}P(N=k)x^k=\text{e}^{-\lambda}\sum_{k=0}^{+\infty}\frac{(\lambda x)^k}{k!}=\text{e}^{-\lambda(1-x)}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-68d79c75e2d906ea92d837c42d388852_l3.png)
b/ La fonction simulX(n) simule une répétition de ![]() expériences identiques et indépendantes qui a deux issues et elle compte le nombre de succès, où un succès est de probabilité
expériences identiques et indépendantes qui a deux issues et elle compte le nombre de succès, où un succès est de probabilité ![]() . Par conséquent, simulX(n) simule une loi binomiale de paramètres
. Par conséquent, simulX(n) simule une loi binomiale de paramètres ![]() .
.
c/ Le programme est le suivant :
function s=simulS(lambda,n)
N=grand(1,1, »poi »,lambda)
s=0;
if N>=1 then
for k=1:N
s=s+simulX(n)
end
end
endfunction
11/ a/ Soit ![]() et
et ![]() . Dans toute cette question, on admet que
. Dans toute cette question, on admet que ![]() .
.
Sachant ![]() , pour tout
, pour tout ![]() ,
, ![]() prend ses valeurs dans
prend ses valeurs dans ![]() et admet donc une espérance. De plus, les variables aléatoires
et admet donc une espérance. De plus, les variables aléatoires ![]() suivent la même loi donc sachant
suivent la même loi donc sachant ![]() , elles admettent même espérance. Par conséquent,
, elles admettent même espérance. Par conséquent,
![Rendered by QuickLaTeX.com \[\dis \sum_{i=1}^{n+1}E(X_i|S_{n+1}=k)=(n+1)E(X_1|S_{n+1}=k)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e304f27e67e95edf4d6d886674c2ae04_l3.png)
De plus, par linéarité de l’espérance,
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}E(X_i|S_{n+1}=k)=E\left(\sum_{i=1}^{n+1}X_i|S_{n+1}=k\right)=E(S_{n+1}|S_{n+1}=k)=k\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5637776dfb7d327b49d111647ac3c223_l3.png)
On en déduit que pour tout
b/ Soit ![]() . Par définition des probabilités conditionnelles,
. Par définition des probabilités conditionnelles,
![]()
Or, par mutuelle indépendance des variables aléatoires
![]()
c/ Avec la question précédente,
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}{\dis \sum_{j=0}^k\left(a+\frac{bj}{k}\right)q_jP(S_n=k-j)}&=&{\dis P(S_{n+1}=k)\left[\sum_{j=0}^k\left(a+\frac{bj}{k}\right)P_{[S_{n+1}=k]}(X_{n+1}=j)\right]}\\&=& P(S_{n+1}=k)E\left(a+\frac{bX_{n+1}}{k} |S_{n+1}=k\right)\\&=&P(S_{n+1}=k)\left(a+\frac{b}{k}E(X_{n+1}|S_{n+1}=k)\right)\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-30862fdd6652c93ec21c7d37d39559a1_l3.png)
par linéarité de l’espérance et parce que sachant
Avec le résultat de la question 11.a,
![Rendered by QuickLaTeX.com \[{\dis \sum_{j=0}^k\left(a+\frac{bj}{k}\right)q_jP(S_n=k-j)}=P(S_{n+1}=k)\left(a+\frac{b}{n+1}\right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6768ddaf4d3b2ba302c9f00ae7e75ace_l3.png)
12/ a/ La famille ![]() est un système complet d’événements. D’après la formule des probabilités totales, pour tout
est un système complet d’événements. D’après la formule des probabilités totales, pour tout ![]() ,
,
![Rendered by QuickLaTeX.com \[P(S=k-j)=\dis \sum_{n=0}^{+\infty}P((S=k-j)\cap (N=n))=\sum_{n=0}^{+\infty}P((S_n=k-j)\cap (N=n))=\sum_{n=0}^{+\infty}P(S_n=k-j)p_n\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-047d6a9a0dcbf1a53d5759db9cfc8962_l3.png)
par indépendance des variables aléatoires ![]() et donc des
et donc des ![]() avec la variable aléatoire
avec la variable aléatoire ![]() .
.
b/ Avec le résultat de la question précédente,
![Rendered by QuickLaTeX.com \[\dis \sum_{j=0}^k\left(a+\frac{bj}{k}\right)q_jP(S=k-j)=\sum_{j=0}^k\sum_{n=0}^{+\infty}\left(a+\frac{bj}{k}\right)p_nq_jP(S_n=k-j)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f610d94f40068a7281bcf371184de377_l3.png)
Or, pour tout ![]() , la série de terme général
, la série de terme général ![]() converge d’après la question 12.a. On a donc
converge d’après la question 12.a. On a donc
![Rendered by QuickLaTeX.com \[\dis \sum_{j=0}^k\left(a+\frac{bj}{k}\right)q_jP(S=k-j)=\sum_{n=0}^{+\infty}p_n\left[\sum_{j=0}^k\left(a+\frac{bj}{k}\right)q_jP(S_n=k-j)\right]\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9798867ce06c27352be0782dada57a50_l3.png)
Or pour tout
![Rendered by QuickLaTeX.com \[\sum_{j=0}^k\left(a+\frac{bj}{k}\right)q_jP(S_n=k-j)=\left(a+\frac{b}{n+1}\right)P(S_{n+1}=k)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b2dbe367fac355a620c69bf99b1c2bd3_l3.png)
D’où, ![]() .
.
Or, pour tout ![]() ,
, ![]() car
car ![]() vérifie une relation de Panjer. On a donc bien
vérifie une relation de Panjer. On a donc bien
![Rendered by QuickLaTeX.com \[\dis \sum_{j=0}^k\left(a+\frac{bj}{k}\right)q_jP(S=k-j)=\sum_{n=0}^{+\infty}p_{n+1}P(S_{n+1}=k)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a4d268431b7f03637e96637b6993fd3d_l3.png)
c/ La famille ![]() est un système complet d’événements. D’après la formule des probabilités totales, en reprenant le raisonnement de la question 12.a,
est un système complet d’événements. D’après la formule des probabilités totales, en reprenant le raisonnement de la question 12.a,
![Rendered by QuickLaTeX.com \[P(S=k)=\dis \sum_{m=1}^{+\infty}P(S_m=k)P(N=m)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-abf72d02976b5154728f640bff4fc02b_l3.png)
car comme
![Rendered by QuickLaTeX.com \[P(S=k)=\dis \sum_{n=0}^{+\infty}p_{n+1}P(S_{n+1}=k)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5870a7f8ae0c447a6acf38d5579d5f8a_l3.png)
d/ Avec les résultats des deux question précédentes, on a
![Rendered by QuickLaTeX.com \[\dis \sum_{j=1}^k\left(a+\frac{bj}{k}\right)q_jP(S=k-j)=(1-aq_0)P(S=k)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-93995259b5591dc2c1f109a12d0d6682_l3.png)
Or ![]() et
et ![]() , par conséquent
, par conséquent ![]() . D’où
. D’où
![Rendered by QuickLaTeX.com \[P(S=k)=\frac{1}{1-aq_0}\sum_{j=1}^k\left(a+\frac{bj}{k}\right)q_jP(S=k-j)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f2a327ea3756dce57033adea8d7e49ae_l3.png)

