Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet ECRICOME Maths ECS 2019
Revenir à tous les corrigés des annales maths Ecricome
Exercice 1 : Intégrale de Wallis
1/ La fonction cosinus est continue sur ![]() ainsi que la fonction polynomiale
ainsi que la fonction polynomiale ![]() donc par composition la fonction
donc par composition la fonction ![]() est continue sur
est continue sur ![]() donc on peut l’intégrer sur le segment
donc on peut l’intégrer sur le segment ![]() et
et ![]() est bien définie.
est bien définie.
On a ![]() .
.
![]()
Pour la suite on utilise la relation ![]() vraie pour tout
vraie pour tout ![]() dans
dans ![]() On a en particulier
On a en particulier ![]()
Donc ![]()
Par conséquent ![]()
2/ a/ On calcule le signe de
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}I_{n+1}-I_n&=& \displaystyle \int_0^{\frac{\pi}{2}}(\cos t)^{n+1} \text{d}t-\int_0^{\frac{\pi}{2}}(\cos t)^{n} \text{d}t \\&=& \displaystyle \int_0^{\frac{\pi}{2}}\left((\cos t)^{n+1}-(\cos t)^{n}\right)\text{d}t = \int_0^{\frac{\pi}{2}}\left(\cos t-1\right)(\cos t)^{n}\text{d}t.\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6c4fffae89a22b9494d27243d54fa3b9_l3.png)
Pour tout
![]()
Donc la suite
en intégrant selon
![]()
Donc la suite
2/ b/ On remarque ![]()
On pose ![]() et
et ![]() puis
puis ![]() les fonctions
les fonctions ![]() sont
sont ![]() sur
sur ![]() et
et
![]()
![]()
Bilan : Pour tout ![]()
2/ c/ Ce qui précède assure que ![]() donc
donc ![]() donc
donc ![]()
On pose alors ![]()
Avec ![]() et
et ![]() , on voit que
, on voit que ![]() est vraie.
est vraie.
Supposons ![]() vraie, on a alors
vraie, on a alors ![]()
![]()
![]()
![]()
![]()
![]()
Puis
![]()
![]()
![]()
![]()
![]()
![]()
Donc ![]() est vraie.
est vraie.
Conclusion : pour tout ![]() est vraie.
est vraie.
2/ d/ function y=I(n)
u=zeros(1,2*n+2)
//u(0)= pi/2 ce terme n’existe pas dans le tableau
u(1) = 1
u(2) = pi/4
for k=1:n
u(2*k+1) = (2*k)*u(2*k-1)/(2*k+1)
u(2*k+2) = (2*k+1)*u(2*k)/(2*k+2)
end
y = u
endfunction
3/ a/ D’après le cours, ![]() et
et ![]()
3/ b/ Pour tout ![]() on a
on a ![]() donc
donc ![]() et on peut composer par
et on peut composer par ![]() . Ainsi
. Ainsi ![]() or
or ![]() donc
donc
![]()
On en déduit que ![]() , en composant cette limite par exponentielle, il vient
, en composant cette limite par exponentielle, il vient
![]()
3/ c/ Avec un raisonnement analogue,
![]()
donc
On en déduit que ![]() , en composant cette limite par exponentielle, il vient
, en composant cette limite par exponentielle, il vient
![]()
4/ a/ Soit ![]() sur
sur ![]() est dominé par 1 donc en intégrant avec
est dominé par 1 donc en intégrant avec ![]() on a
on a
![]()
4/ b/ Soit ![]() sur
sur ![]() est décroissante donc dominée par
est décroissante donc dominée par ![]() donc en intégrant avec
donc en intégrant avec ![]() on a
on a
![]()
4/ c/ On utilise la relation de Chasles, les questions 3(b), 4(a), 4(b) et le fait que ![]() est positive,
est positive,
![]()
Donc par encadrement
5/ a/ Soit ![]() On utilise la relation de Chasles
On utilise la relation de Chasles
![]()
Sur
Donc ![]() , on utilise une fois de plus le fait que
, on utilise une fois de plus le fait que ![]() est décroissante sur
est décroissante sur ![]() pour minorer,
pour minorer,
![]()
A la question 3(c), il est vu que ![]() donc
donc ![]()
Or ![]() donc la série de Riemann
donc la série de Riemann ![]() diverge donc par comparaison des séries à terme général positif, la série
diverge donc par comparaison des séries à terme général positif, la série ![]() diverge et par comparaison la série
diverge et par comparaison la série ![]() diverge.
diverge.
5/ b/ function S=somme(n)
S = pi/2
tableau = I(floor(n/2)) sinon on laisse I(n), tant pis pour les termes superflus
for j=1:n
S=S+tableau(j)
end
endfunction
6/ a/ Soit ![]()
6/ b/ La fonction ![]() est continue sur le segment
est continue sur le segment ![]() donc l’intégrale
donc l’intégrale ![]() est bien définie. On applique le changement de variables
est bien définie. On applique le changement de variables ![]() de classe
de classe ![]() avec
avec ![]()
Avec ![]() et avec
et avec ![]() donc
donc
![]()
6/ c/ Soit ![]() on utilise la linéarité de l’intégration,
on utilise la linéarité de l’intégration,
![Rendered by QuickLaTeX.com \[\sum_{k=0}^n(-1)^k I_k = \sum_{k=0}^n\int_{0}^{\pi/2}(-1)^k(\cos(t))^k \text{d}t = \int_{0}^{\pi/2} \sum_{k=0}^n (-\cos(t))^k \text{d}t.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-be993dced1bca01b1968c45c78d534f6_l3.png)
Or sur ![]() donc
donc ![]() De plus la fonction
De plus la fonction ![]() est continue sur le segment
est continue sur le segment ![]() , donc
, donc
![Rendered by QuickLaTeX.com \[\sum_{k=0}^n(-1)^k I_k = \int_{0}^{\pi/2}\frac{1}{1+\cos(t)} \text{d}t - \int_{0}^{\pi/2}\frac{-(-\cos(t))^{n+1}}{1+\cos(t)}\text{d}t\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5489c74f2263b48120a61499363212c5_l3.png)
6/ d/ On utilise la positivité de l’intégration avec le fait que ![]()
![Rendered by QuickLaTeX.com \[\left\vert \int_{0}^{\pi/2}\frac{-(-\cos(t))^{n+1}}{1+\cos(t)}\text{d}t\right\vert \le \int_{0}^{\pi/2}\left\vert\frac{-(-\cos(t))^{n+1}}{1+\cos(t)}\right\vert\text{d}t = \int_{0}^{\pi/2}\frac{\vert\cos(t)\vert^{n+1}}{1+\cos(t)}\text{d}t = \int_{0}^{\pi/2}\frac{\cos(t)^{n+1}}{1+\cos(t)}\text{d}t .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-56f6cc18fc8c6df553dfea944c3e12b3_l3.png)
On a
![Rendered by QuickLaTeX.com \[\left\vert \int_{0}^{\pi/2}\frac{-(-\cos(t))^{n+1}}{1+\cos(t)}\text{d}t\right\vert \le \int_{0}^{\pi/2}{\cos(t)^{n+1}}\text{d}t =I_{n+1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d32b8f3e047ec92d2314aa46243a805f_l3.png)
6/ e/ On en déduit avec 6(c) puis 6(b) que
![Rendered by QuickLaTeX.com \[\left\vert \int_{0}^{\pi/2}\frac{-(-\cos(t))^{n+1}}{1+\cos(t)}\text{d}t\right\vert =\left\vert \sum_{k=0}^n(-1)^k I_k - \int_{0}^{\pi/2}\frac{1}{1+\cos(t)} \text{d}t \right\vert = \left\vert \sum_{k=0}^n(-1)^k I_k -1 \right\vert \le I_{n+1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0d024f98683291f43f4e165fba443039_l3.png)
Or la suite ![]() converge vers 0 selon 4(c), donc par encadrement
converge vers 0 selon 4(c), donc par encadrement
![Rendered by QuickLaTeX.com \[\left\vert \sum_{k=0}^n(-1)^k I_k -1 \right\vert\underset{n\to +\infty}{\longrightarrow} 0 \text{ donc } \sum_{k=0}^n(-1)^k I_k\underset{n\to +\infty}{\longrightarrow} 1.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e4668358ca217cca50f0bef6433b965f_l3.png)
Conclusion : la série ![]() converge et sa somme vaut 1.
converge et sa somme vaut 1.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Diagonalisation de Matrices
1/ Le calcul donne ![]() Donc
Donc ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]() , les racines sont
, les racines sont ![]() et
et ![]() donc le spectre de
donc le spectre de ![]() est inclus dans
est inclus dans ![]()
On remarque que 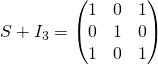 qui n’est pas inversible car il y a deux colonnes égales donc
qui n’est pas inversible car il y a deux colonnes égales donc ![]() est valeur propres de
est valeur propres de ![]()
On remarque que 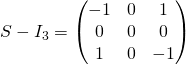 qui n’est pas inversible car il y a une colonne nulle donc
qui n’est pas inversible car il y a une colonne nulle donc ![]() est valeur propres de
est valeur propres de ![]()
Finalement le spectre de ![]() est
est ![]()
2/ On applique la définition de ![]()
![Rendered by QuickLaTeX.com \[\begin{pmatrix} a\\ b\\ c\end{pmatrix}\in F\Longleftrightarrow a=c\Longleftrightarrow\begin{pmatrix} a\\ b\\ c\end{pmatrix} = a\begin{pmatrix} 1\\ 0\\ 1\end{pmatrix}+b\begin{pmatrix} 0\\ 1\\0\\ \end{pmatrix}\Longleftrightarrow\begin{pmatrix} a\\ b\\ c\end{pmatrix}\in\text{Vect}\left( \begin{pmatrix} 1\\ 0\\ 1\end{pmatrix},\begin{pmatrix} 0\\ 1\\0\\ \end{pmatrix} \right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-35c35049eceb90632ac2d5d19dd45485_l3.png)
Donc 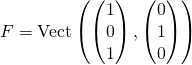 , par conséquent
, par conséquent 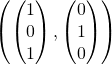 engendre
engendre ![]() et ces deux vecteurs ne sont pas colinéaires donc ils forment une famille libre et donc une base de
et ces deux vecteurs ne sont pas colinéaires donc ils forment une famille libre et donc une base de ![]()
On applique la définition de ![]()
![Rendered by QuickLaTeX.com \[\begin{pmatrix} a\\ b\\ c\end{pmatrix}\in G\Longleftrightarrow a=-c \text{ et } b=-b \Longleftrightarrow\begin{pmatrix} a\\ b\\ c\end{pmatrix} = a\begin{pmatrix} 1\\ 0\\ -1\end{pmatrix}\Longleftrightarrow\begin{pmatrix} a\\ b\\ c\end{pmatrix}\in\text{Vect}\left( \begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix} \right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-77f5d63859f4afb538eb5e920cd05532_l3.png)
Donc 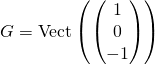 , par conséquent
, par conséquent 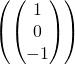 engendre
engendre ![]() et ce vecteur n’est pas nul donc il forme une famille libre et donc une base de
et ce vecteur n’est pas nul donc il forme une famille libre et donc une base de ![]()
Pour trouver une base du sous-espace propre de S associé à la valeur propre ![]() (noté
(noté ![]() ) , on caractérise l’appartenance par une combinaison linéaire,
) , on caractérise l’appartenance par une combinaison linéaire,


![]()
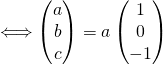
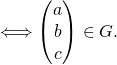
Donc ![]()
De même 
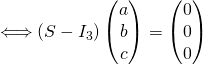
![]()
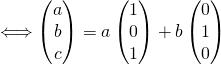
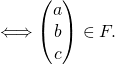
Donc ![]()
3/ En tant que sous-espaces propres associées à des valeurs propres distinctes, ![]() et
et ![]() sont en somme directe, la somme de leurs dimensions vaut 3 qui est celle de
sont en somme directe, la somme de leurs dimensions vaut 3 qui est celle de ![]() donc
donc ![]() et
et ![]() sont supplémentaires de
sont supplémentaires de ![]() .
.
4/ a/ Dans la colonne 1 de ![]() , tous les termes sont nuls sauf celui sur la ligne
, tous les termes sont nuls sauf celui sur la ligne ![]()
Dans la colonne 2 de ![]() , tous les termes sont nuls sauf celui sur la ligne
, tous les termes sont nuls sauf celui sur la ligne ![]()
Et ainsi de suite jusqu’à la colonne ![]() o\`u tous les termes sont nuls sauf celui sur la ligne
o\`u tous les termes sont nuls sauf celui sur la ligne ![]()
Donc
![Rendered by QuickLaTeX.com \[S= \begin{pmatrix} 0 &\hdots &0& 0&1\\ 0&\hdots &0&1&0\\\vdots & \iddots& \iddots & \iddots & \vdots \\ 0&1&0&\hdots &0\\ 1&0&\hdots &0& 0\end{pmatrix} .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-77921b93b7f86b2dfc785e8bb2168ec2_l3.png)
4/ b/  Cette question en apparence anodine présente un intérêt pour la suite si on remarque que
Cette question en apparence anodine présente un intérêt pour la suite si on remarque que ![]() est symétrique si et seulement si
est symétrique si et seulement si ![]() et que
et que ![]() est antisymétrique si et seulement si
est antisymétrique si et seulement si ![]()
4/ c/ Dans la suite, pour toute matrice ![]() , on note
, on note ![]() son coefficient en ligne
son coefficient en ligne ![]() et colonne
et colonne ![]()
On a alors ![]() .
.
Or les ![]() valent 0 ou 1 donc
valent 0 ou 1 donc ![]() vaut 0 ou 1, et
vaut 0 ou 1, et ![]() vaut 1 si et seulement si
vaut 1 si et seulement si ![]() si et seulement si
si et seulement si ![]() et
et ![]() si et seulement si
si et seulement si ![]() .
.
Par conséquent si ![]() alors
alors ![]()
Si ![]() alors
alors ![]() Dans cette somme tous les termes sont nuls sauf celui pour
Dans cette somme tous les termes sont nuls sauf celui pour ![]() et ce terme
et ce terme ![]() vaut 1 donc la somme vaut 1.
vaut 1 donc la somme vaut 1.
Bilan : ![]()
5/ a/ On s’inspire de la démonstration de cours par analyse-synthèse qui montre que toute matrice ![]() est somme d’une matrice symétrique :
est somme d’une matrice symétrique : ![]() et d’une matrice antisymétrique :
et d’une matrice antisymétrique : ![]()
Analyse : On suppose qu’il existe ![]() tel que
tel que ![]()
On utilise la remarque faite en 4(b), on multiplie par ![]() et
et ![]() car
car ![]() est symétrique et
est symétrique et ![]() est antisymétrique.
est antisymétrique.
Donc ![]() et
et ![]() donc, en cas d’existence,
donc, en cas d’existence, ![]() et
et ![]() sont uniques et valent respectivement
sont uniques et valent respectivement ![]() et
et ![]() .
.
Synthèse : Il est immédiat que ![]()
De plus ![]() donc
donc ![]()
Et ![]() donc
donc ![]()
Bilan : il existe un unique couple ![]() tel que
tel que ![]() et
et ![]()
5/ b/ Avec 4(c), on sait que ![]() donc
donc ![]() est annulateur de
est annulateur de ![]() donc le spectre de
donc le spectre de ![]() est inclus dans
est inclus dans ![]() On sait aussi que
On sait aussi que ![]() est diagonalisable. Si
est diagonalisable. Si ![]() n’a qu’une valeur propre
n’a qu’une valeur propre ![]() alors
alors ![]() ce qui est absurde car
ce qui est absurde car ![]() Donc
Donc ![]() a au moins deux valeurs propres donc le spectre de
a au moins deux valeurs propres donc le spectre de ![]() est
est ![]()
On utilise ensuite la remarque de la question 4(b) ainsi
![]()
et
![]()
Donc ![]() et
et ![]() sont les sous-espaces propres de
sont les sous-espaces propres de ![]() avec les valeurs propres respectives 1 et
avec les valeurs propres respectives 1 et ![]()
6/ a/ Soit ![]()
![]() car
car ![]() est nul sauf si
est nul sauf si ![]() et dans ce cas il vaut 1.
et dans ce cas il vaut 1.
D’autre part ![]() car
car ![]() est nul sauf si
est nul sauf si ![]() et dans ce cas il vaut 1.
et dans ce cas il vaut 1.
Or l’énoncé dit que ![]() donc
donc ![]() et cela pour tout
et cela pour tout ![]() Donc
Donc ![]()
6/ b/ On sait que ![]() donc
donc ![]() car
car ![]() est un réel.
est un réel.
Avec le calcul de 4(b), on voit que si ![]() est non nulle alors
est non nulle alors ![]() le sera aussi car on retrouve les mêmes coefficients dans l’ordre inversé donc comme
le sera aussi car on retrouve les mêmes coefficients dans l’ordre inversé donc comme ![]() est vecteur propre, il est non nul donc
est vecteur propre, il est non nul donc ![]() est aussi non nul.
est aussi non nul.
Bilan : ![]() est vecteur propre de
est vecteur propre de ![]() associé à
associé à ![]()
6/ c/ On calcule ![]()
6/ d/ Si ![]() est nul alors
est nul alors ![]() donc
donc ![]() est antisymétrique tout en étant un vecteur propre de
est antisymétrique tout en étant un vecteur propre de ![]() associé à
associé à ![]()
Si ![]() est non nul alors comme
est non nul alors comme ![]() ,
, ![]() est vecteur propre de
est vecteur propre de ![]() associé à
associé à ![]() et de plus
et de plus ![]() donc
donc ![]() est symétrique.
est symétrique.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Problème : Probabilités Discrètes
1/ Avant le deuxième tirage c’est-à-dire après le premier, il y a soit 2 blanches (B) et une noire (N) si on a pioché N au premier tour. Si on pioche B au premier tour, on aura 2 N et une B.
Donc ![]() On a
On a ![]() donc
donc ![]() On reconnaît une loi uniforme sur
On reconnaît une loi uniforme sur ![]() Ainsi
Ainsi ![]() et
et ![]()
2/ Lors de deux tirages, on peut extraire 2 N ou 2 B ou bien 1 N et 1 B donc ![]() peut valoir 3 ou 2 ou 1 donc
peut valoir 3 ou 2 ou 1 donc ![]()
![]() est réalisé si et seulement si
est réalisé si et seulement si ![]() est réalisé donc
est réalisé donc
![]()
De même ![]() est réalisé si et seulement si
est réalisé si et seulement si ![]() est réalisé donc
est réalisé donc
![]()
Donc ![]()
3/ Sachant qu’il y a une blanche et une noire au début, lors de ![]() tirages on peut extraire entre 0 et
tirages on peut extraire entre 0 et ![]() blanches donc après ceux-ci, l’urne peut contenir entre 1 blanche et
blanches donc après ceux-ci, l’urne peut contenir entre 1 blanche et ![]() blanches donc
blanches donc ![]()
4/ Soit ![]() Il est immédiat qu’après le
Il est immédiat qu’après le ![]() tirage, il y a
tirage, il y a ![]() boules dans l’urne car une ajoute une boule à chaque tirage. Donc après le
boules dans l’urne car une ajoute une boule à chaque tirage. Donc après le ![]() tirage, il y a
tirage, il y a ![]() boules dans l’urne. Le tirage
boules dans l’urne. Le tirage ![]() amène une B ou une N donc à son issue, le nombre de B est stable ou est augmenté de 1. Donc si
amène une B ou une N donc à son issue, le nombre de B est stable ou est augmenté de 1. Donc si ![]() et
et ![]() alors
alors ![]()
Selon le protocole, le nombre de B est stable après un tirage si et seulement si on sort une B donc ![]() est la probabilité de sortir une B dans une urne contenant
est la probabilité de sortir une B dans une urne contenant ![]() B et
B et ![]() boules donc
boules donc ![]()
Selon le protocole, le nombre de B est augmenté de 1 après un tirage si et seulement si on sort une N donc ![]() est la probabilité de sortir une N dans une urne contenant
est la probabilité de sortir une N dans une urne contenant ![]() B et
B et ![]() boules donc
boules donc ![]()
5/ Soit ![]() si
si ![]() alors
alors ![]() et comme
et comme ![]() on a aussi
on a aussi ![]() donc la formule
donc la formule ![]() est vraie.
est vraie.
Supposons ![]() alors
alors ![]() est réalisé si et seulement si
est réalisé si et seulement si ![]() est réalisé car le nombre maximal de B après
est réalisé car le nombre maximal de B après ![]() tirages est
tirages est ![]() Donc
Donc ![]() Or
Or ![]() donc
donc ![]() donc la formule
donc la formule
![]()
est vraie pour
Supposons ![]() On applique la formule des probabilités totales avec le système complet d’événements
On applique la formule des probabilités totales avec le système complet d’événements ![]() ce qui donne
ce qui donne
![Rendered by QuickLaTeX.com \[\mathbb{P}\left( \left[ X_{k+1}=i\right] \right) =\sum_{j=1}^{k+1} \mathbb{P}(X_k=j)\mathbb{P}_{[X_k=j]}( X_{k+1}=i)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4d911b2515746259d09507c9b5820b37_l3.png)
or
![]()
On a vu que
Si ![]() alors
alors ![]() et la formule
et la formule ![]() est valable pour
est valable pour ![]() , sinon la question précédente avec
, sinon la question précédente avec ![]() donne
donne ![]()
Finalement on a bien dans tous les cas
![]()
6/ On a ![]() et
et ![]()
puis
![]()
et
7/ a/ On reprend la question 5 avec ![]() et
et ![]() ainsi, pour tout
ainsi, pour tout ![]() , on a\\
, on a\\ ![]() Avec
Avec ![]() une récurrence simple donne
une récurrence simple donne ![]()
7/ b/ On reprend la question 5 avec ![]() et
et ![]() ainsi, pour tout
ainsi, pour tout ![]() , on a
, on a ![]() Avec
Avec ![]() une récurrence simple donne
une récurrence simple donne ![]()
7/ c/ Soit ![Rendered by QuickLaTeX.com k\in\mathbb{N}, a_{k+1}=(k+2)!\mathbb{P}(X_{k+1}=2) = (k+2)!\left(\frac{2}{k+2}{\ P}\left( \left[X_{k}=2\right] \right) +\frac{3+k-2}{k+2}\mathbb{\ }P\left( \left[ X_{k}=1\right] \right)\right)](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8263b01f0b317a095522e3b8683f7244_l3.png)
donc ![]()
![]()
![]()
![]() La suite
La suite ![]() est géométrique de raison 2 donc, pour tout
est géométrique de raison 2 donc, pour tout ![]()
![]() car
car ![]() Donc
Donc ![]() et
et ![]()
8/ La ligne 5 simule une loi uniforme sur ![]() en effet
en effet ![]() simule une loi uniforme sur
simule une loi uniforme sur ![]() donc
donc ![]() simule une loi uniforme sur
simule une loi uniforme sur ![]() donc
donc ![]() simule une loi uniforme sur
simule une loi uniforme sur ![]() en prenant la partie entière
en prenant la partie entière ![]() simule une loi uniforme sur
simule une loi uniforme sur ![]() . Donc
. Donc ![]() est un nombre entier choisi au hasard dans
est un nombre entier choisi au hasard dans ![]() , on peut considérer que les boules N ont les numéros 1 à
, on peut considérer que les boules N ont les numéros 1 à ![]() et que les blanches ont les numéros
et que les blanches ont les numéros ![]() à
à ![]() . Ainsi
. Ainsi ![]() est le nombre de N et
est le nombre de N et ![]() le nombre de B. Donc si
le nombre de B. Donc si ![]() , on a sorti une B et
, on a sorti une B et ![]() est augmenté de 1 sinon on a sorti une N et
est augmenté de 1 sinon on a sorti une N et ![]() augmenté de 1.
augmenté de 1.
![]() et
et ![]() sont initialisés à 1 ensuite on simule
sont initialisés à 1 ensuite on simule ![]() tirages et on retourne
tirages et on retourne ![]() le nombre de B à la fin des ces tirages. On a donc simuler
le nombre de B à la fin des ces tirages. On a donc simuler ![]()
9/ On calcule les effectifs de chaque valeur entre 1 et ![]() puis on divise par
puis on divise par ![]() pour avoir les fréquences. On passe sur le tiret du nom de la fonction qui n’est correct syntaxiquement.
pour avoir les fréquences. On passe sur le tiret du nom de la fonction qui n’est correct syntaxiquement.
function LE = loiExpo(k,N)
LE=zeros(1,k+1)
for j=1:N
valeur = mystere(k)
LE(valeur) = LE(valeur) + 1
end
LE = LE/N
endfunction
10/ La matrice ![]() est telle que
est telle que ![]() on retourne donc la n-ème ligne de
on retourne donc la n-ème ligne de ![]()
function LT=loiTheo(n)
M=zeros(n,n+1)
M(1,1)=1/2
M(1,2)=1/2
for k=1:n-1
M(k+1,1)=M(k,1)/(k+2)
for i=2:k+1
M(k+1,i)=(i/(k+2))*M(k,i)+(3+k-i)/(k+2)*M(k,i-1)
end
M(k+1,k+2)=M(k+1,1)
end
LT=M(n,:)
endfunction
11/ En théorie ![]() or dans le tableau les valeurs sont distinctes donc c’est un calcul expérimental avec
or dans le tableau les valeurs sont distinctes donc c’est un calcul expérimental avec ![]() .
.
12/ a/ ![]() a un support fini donc a une espérance. On utilisera le fait que si
a un support fini donc a une espérance. On utilisera le fait que si ![]() n’est pas dans le support de
n’est pas dans le support de ![]() alors
alors ![]() . On emploiera aussi le théorème de transfert. On a
. On emploiera aussi le théorème de transfert. On a
![Rendered by QuickLaTeX.com \noindent E(X_{k+1})=\sum_{i=1}^{k+2} i\mathbb{P}(X_{k+1}=i) = \sum_{i=1}^{k+2} i\left( \frac{i}{k+2}{\ P}\left( \left[X_{k}=i\right] \right) +\frac{3+k-i}{k+2}\mathbb{P}\left( \left[ X_{k}=i-1\right] \right) \right)](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f15f7594807ffebbad91cbe542307811_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
12/ b/ Pour tout ![]() on pose
on pose ![]()
![]() est vraie car
est vraie car ![]() constant de valeur 1 donc de moyenne 1.
constant de valeur 1 donc de moyenne 1.
Si ![]() vraie à un rang
vraie à un rang ![]() alors
alors ![]() donc
donc ![]() vraie.
vraie.
Bilan : Pour tout ![]()
![]()
12/ c/ Il y a autant de B que de N au début de l’expérience, on ajoute une B ou une N à chaque tirage, donc par symétrie, ![]() et
et ![]() ont la même loi et la même espérance. De plus on a toujours
ont la même loi et la même espérance. De plus on a toujours ![]() qui vaut le nombre de boules après
qui vaut le nombre de boules après ![]() tirages donc
tirages donc ![]() donc
donc ![]() donc
donc ![]()
13/ a/ La variable ![]() a une variance donc
a une variance donc ![]() en a une aussi et on peut appliquer la formule de Bienaymé-Tchebychev
en a une aussi et on peut appliquer la formule de Bienaymé-Tchebychev
![Rendered by QuickLaTeX.com \[\forall \alpha >0, \quad \mathbb{P}\left(\left\vert\frac{X_k}{k+2}-E\left(\frac{X_k}{k+2}\right)\right\vert\ge \alpha\right) \le \frac{V\left(\frac{X_k}{k+2}\right)}{\alpha^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7f8d2440cdb5f73539b4c3b06ffad82e_l3.png)
donc
![]()
en utilisant
Donc ![]() par
par
encadrement.
Donc ![]()
![]() représente la proportion de boules blanches dans l’urne après
représente la proportion de boules blanches dans l’urne après ![]() tirages, intuitivement cette proportion a tendance à être proche de
tirages, intuitivement cette proportion a tendance à être proche de ![]() quand
quand ![]() est grand.
est grand.
13/ b/ ![]() représente la proportion de boules blanches dans l’urne après
représente la proportion de boules blanches dans l’urne après ![]() tirages, intuitivement cette proportion a tendance à être proche de
tirages, intuitivement cette proportion a tendance à être proche de ![]() quand
quand ![]() est grand.
est grand.
14/ a/ Soit ![]() dans
dans ![]() et
et ![]() on a
on a
![]()
![]()
Donc ![]() est linéaire.
est linéaire.
14/ b/ Si ![]() est nul alors
est nul alors ![]() est nul aussi.
est nul aussi.
Si ![]() avec
avec ![]() alors
alors ![]() aura le même terme dominant que
aura le même terme dominant que ![]() car les autres termes sont tous de degrés inférieurs stricts à
car les autres termes sont tous de degrés inférieurs stricts à ![]() donc le terme dominant de
donc le terme dominant de ![]() est
est ![]() donc par somme
donc par somme
comme ![]() le terme dominant de
le terme dominant de ![]() sera
sera ![]() avec
avec ![]()
Donc ![]() et
et ![]() ont le même degré.
ont le même degré.
14/ c/ On voit donc que si ![]() n’est pas nul alors
n’est pas nul alors ![]() ne l’est pas non plus donc le noyau de
ne l’est pas non plus donc le noyau de ![]() ne contient que le polynôme nul et
ne contient que le polynôme nul et ![]() est injective.
est injective.
14/ d/ On a vu que l’unique antécédent de ![]() est
est ![]() lui-même.
lui-même.
Soit ![]() non nul de degré
non nul de degré ![]() on sait que les antécédents éventuels de
on sait que les antécédents éventuels de ![]() par
par ![]() sont de degré
sont de degré ![]() donc ils sont dans
donc ils sont dans ![]() . On a vu que
. On a vu que ![]() préserve le degré donc
préserve le degré donc ![]() est stable par
est stable par ![]() donc la restriction de
donc la restriction de ![]() à
à ![]() est un endomorphisme de
est un endomorphisme de ![]() qui est de dimension finie. Comme
qui est de dimension finie. Comme ![]() est injective sur
est injective sur ![]() , elle l’est aussi sur
, elle l’est aussi sur ![]() donc la restriction de
donc la restriction de ![]() à
à ![]() est bijective donc
est bijective donc ![]() a un antécédent par
a un antécédent par ![]() .
.
15/ a/ Par définition, ![]() or
or ![]() donc
donc ![]()
Et ![]() On remarquera que
On remarquera que ![]() en général est défini une somme de réels donc est un polynôme constant.
en général est défini une somme de réels donc est un polynôme constant.
15/ b/ On a ![]() or
or
![]()
![]()
![]()
donc ![]()
16/ a/ ![]() s’écrit :
s’écrit : ![]()
C’est vrai car on sait que ![]() et
et ![]()
16/ b/ Soit ![]() on suppose
on suppose ![]() vraie, soit
vraie, soit ![]()
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}\alpha_{k+1}&=&(k+2)!\mathbb{P}(X_{k+1}=i)-\sum\limits_{j=1}^{i-1}P_{i,j}(k+1)j^{k+1}\\&=& (k+2)!\left( \frac{i}{k+2}{\mathbb{P}}\left( X_{k}=i\right) +\frac{3+k-i}{k+2}\mathbb{P}\left( X_{k}=i-1\right)\right) -\sum\limits_{j=1}^{i-1}P_{i,j}(k+1)j^{k+1}\text{ avec $(*)$}\\&=& (k+1)!\left(i{\mathbb{P}}\left( X_{k}=i\right) + ({3+k-i} )\mathbb{P}\left( X_{k}=i-1\right)\right) -\sum\limits_{j=1}^{i-1}P_{i,j}(k+1)j^{k+1}\\&=& (k+1)!\left(i{\mathbb{P}}\left( X_{k}=i\right) + ({3+k-i} )\frac{1}{(k+1)!}\sum\limits_{j=1}^{i-1}P_{i-1,j}(k)j^k\right) -\sum\limits_{j=1}^{i-1}P_{i,j}(k+1)j^{k+1} \text{ avec ${\cal H}_{i-1}$}\\&=& (k+1)!i{\mathbb{P}}\left( X_{k}=i\right) + \sum\limits_{j=1}^{i-1}\left(\underbrace{({3+k-i} )P_{i-1,j}(k)}j^k -P_{i,j}(k+1)j^{k+1 }\right)\\&=& (k+1)!i{\mathbb{P}}\left( X_{k}=i\right) + \sum\limits_{j=1}^{i-1}\left(\underbrace{\varphi_{i,j}(P_{i,j}(X))(k)}j^k -P_{i,j}(k+1)j^{k+1 }\right)\\&=& (k+1)!i{\mathbb{P}}\left( X_{k}=i\right) + \sum\limits_{j=1}^{i-1}\left(\underbrace{(jP_{i,j}(X+1)-iP(X))(k)}j^k -P_{i,j}(k+1)j^{k+1 }\right)\\&=& (k+1)!i{\mathbb{P}}\left( X_{k}=i\right) + \sum\limits_{j=1}^{i-1}\left(j^{k+1}P_{i,j}(k+1)-iP_{i,j}(k)j^k -P_{i,j}(k+1)j^{k+1 }\right)\\&=& i\left((k+1)!{\mathbb{P}}\left( X_{k}=i\right) - \sum\limits_{j=1}^{i-1}P_{i,j}(k)j^k\right) = i \alpha_k.\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b4ac8635a330aa65e193b6ab2d19b040_l3.png)
Donc ![]() est géométrique de raison
est géométrique de raison ![]() donc, pour tout
donc, pour tout ![]()
![]()
Or ![]() car
car ![]() donc
donc ![]() .
.
Donc ![]() donc
donc ![]() car
car ![]() est un polynôme constant.
est un polynôme constant.
Donc ![]() .
.
Cela prouve que ![]() est vraie.
est vraie.
16/ c/ Le 16(a) initialise la récurrence, le 16(b) assure l’hérédité donc, pour tout ![]() on a, pour tout
on a, pour tout ![]()
![Rendered by QuickLaTeX.com \[\mathbb{P}\left( X_{k}=i\right) = \frac{1}{(k+1)!}\sum\limits_{j=1}^{i}P_{i,j}(k)j^k .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5ec7b88cfd1aa8bd15ed035275e6b1f4_l3.png)
17/ a/ Au 7(c), il est vu que, pour tout ![]()
![]() .
.
Le 15(a) donne ![]() donc avec la question 16, on a
donc avec la question 16, on a
![Rendered by QuickLaTeX.com \[\mathbb{P}\left( X_{k}=2\right) = \frac{1}{(k+1)!}\sum\limits_{j=1}^{2}P_{2,j}(k)j^k =\frac{1}{(k+1)!}\left( P_{2,1}(k)+P_{2,2}(k)2^k \right)= \frac{1}{(k+1)!}\left( -k-2+2^{k+1} \right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b637e96fdf0d9aec3b6dbdc653ef01c8_l3.png)
Les résultats sont identiques.
17/ b/ Soit ![]()
![Rendered by QuickLaTeX.com \[\mathbb{P}\left( X_{k}=3\right) = \frac{1}{(k+1)!}\sum\limits_{j=1}^{3}P_{3,j}(k)j^k = \frac{1}{(k+1)!}\left( P_{3,1}(k)+P_{3,2}(k)2^k+P_{3,3}(k)3^k \right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3becae09365222ff4e8d84480ff9659a_l3.png)
![]()

