Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet maths EDHEC 2015 ECS
Revenir à tous les corrigés des annales maths BCE
Exercice 1 : convergence de série et intégrales
1. ![]() est continue et positive sur
est continue et positive sur ![]() et
et ![]() . Comme
. Comme ![]() , l’intégrale de Riemann
, l’intégrale de Riemann ![]() converge.
converge.
Conclusion : ![]() converge pour tout
converge pour tout ![]() de
de ![]() .
.
2.a. Nous avons ![]() donc :
donc :
![]()
![]()
2.b. Pour tout ![]() de
de ![]() ,
,
![]()
![]()
![]()
![]() .
.
Comme ![]() et
et ![]() ,
,![]()
3.a. Soit ![]() . On a :
. On a : ![]() .
.
Par croissance de l’intégrale, on a :
![]()
Or ![]()
![]()
![]()
3.b. Comme ![]() , le théorème d’encadrement permet de conclure que
, le théorème d’encadrement permet de conclure que ![]() existe et vaut
existe et vaut ![]()
4.a. ![]()
![]()
![]() ,
,
Par calcul de l’intégrale de Riemann et par linéarité de l’intégrale, ![]()
4.b. Soit ![]() .
. ![]() car
car ![]() . Par croissance de l’intégrale,
. Par croissance de l’intégrale, ![]() . Donc la suite
. Donc la suite ![]() est décroissante.
est décroissante.
4.c. Par (b), pour tout ![]() ,
,
![]()
![]()
donc par d’après la question a, ![]() , et en multipliant par
, et en multipliant par ![]() :
:
![]() .
.
Par encadrement, ![]() ,
,
D’où ![]() .
.
La série de Riemann ![]() diverge, donc la série de terme général
diverge, donc la série de terme général ![]() diverge.
diverge.
5.a. Par un raisonnement analogue à précédemment, on démontre que ![]() .
.
Donc ![]() converge pour tout
converge pour tout ![]() de
de ![]()
5.b. ![]() .
.
![]()
6.a. Soit ![]() . Pour tout
. Pour tout ![]() ,
, ![]()
![]()
![]() , d’où par linéarité,
, d’où par linéarité, ![]()
6.b. Soit ![]()
![]()
![]()
![]()
![]()
![]() par télescopage.
par télescopage.
![]()
6.c. Soit ![]() . On a :
. On a : ![]() .
.
D’après un raisonnement analogue aux questions 3.a et 3.b, on a
![]() , et
, et ![]()
6.d. Par passage à la limite dans la question 6.b, on a
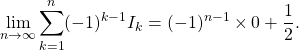
La série de terme général ![]() converge et sa somme vaut
converge et sa somme vaut ![]()
7. n = input(‘entrez une valeur de n supérieure ou égale à 2 :’)}
I= log(2) ; J = 1/2 ; J = I+J
for k = 2:n
I = 1/(k-1) – I ; J = I + J ; end
disp(I, ‘la valeur de I est :’)
disp(J, ‘la valeur de J est :’)
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : convergence d’intégrale
1.a. Soit ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
De plus, pour ![]() ,
, ![]() car
car ![]() .
.
Comme ![]() est de classe
est de classe ![]() sur
sur ![]() ,
, ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
De plus, ![]()
![]()
![]() puisque
puisque ![]() ,
, ![]() est continue sur
est continue sur ![]()
Ainsi ![]() est une variable à densité.
est une variable à densité.
Et par dérivation sur ![]() , une densité de
, une densité de ![]() est :
est :
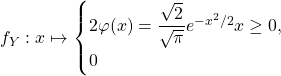
1.b. Soit ![]() .
.
![]()
![]()
![]() .
.
Donc par linéarité ![]() admet une espérance, égale à
admet une espérance, égale à ![]() .
.
1.c. On constate que ![]() . Or d’après la formule de Huygens,
. Or d’après la formule de Huygens, ![]() existe et vaut
existe et vaut ![]() et
et ![]() possède une variance, égale à
possède une variance, égale à ![]()
2.a. La fonction ![]()
![]() est de classe
est de classe ![]() et strictement croissante sur
et strictement croissante sur ![]() , c’est donc une bijection de classe
, c’est donc une bijection de classe ![]() . On va utiliser un changement de variable.
. On va utiliser un changement de variable.
![]() Comme
Comme ![]() ,
, ![]() et
et  .
.
![]() Enfin, pour
Enfin, pour ![]() ,
, ![]() , et pour
, et pour ![]() ,
, ![]() .
.
![]() Le théorème du changement de variable assure alors que
Le théorème du changement de variable assure alors que ![]() est de même nature que
est de même nature que 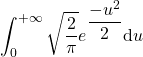 , et que ces intégrales sont égales en cas d’existence.
, et que ces intégrales sont égales en cas d’existence.
![]()
![]() étant une densité,
étant une densité,  existe. Donc les deux intégrales existent.
existe. Donc les deux intégrales existent.
Ainsi, ![]()
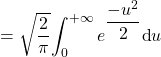
![]()
2.b. ![]() est une densité paire, donc :
est une densité paire, donc :
![]()
![]()
![]()
![]()
De plus, ![]() est positive sur
est positive sur ![]() et continue sur
et continue sur ![]() , donc
, donc ![]() peut être considérée comme une densité.
peut être considérée comme une densité.
3.a. Comme ![]() ,
, ![]() , donc pour
, donc pour ![]() ,
, ![]() .
.
Pour ![]() ,
,
![]() car
car ![]() est positive.
est positive.
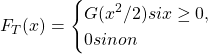
![]() étant de classe
étant de classe ![]() sur
sur ![]() , par composition
, par composition ![]() est de classe
est de classe ![]() sur
sur ![]() , et une densité de
, et une densité de ![]() est donnée par :
est donnée par :
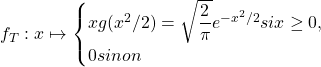
Les densités ![]() et
et ![]() étant identiques,
étant identiques, ![]() suit la même loi que
suit la même loi que ![]()
3.b. ![]() induit
induit ![]() , or
, or ![]() admet une espérance, égale à
admet une espérance, égale à ![]() , valant
, valant ![]() d’après la question 1.c. Par linéarité,
d’après la question 1.c. Par linéarité, ![]() possède une espérance égale à
possède une espérance égale à ![]()
4. x = grand(1,1,’norm’,0,1)} permet de simuler ![]() .
.
y = abs(x)} permet de simuler ![]() , donc
, donc ![]() qui suit la même loi.
qui suit la même loi.
z = y\^{}2/2} permet de simuler ![]() .
.
La valeur absolue ne sert à rien, puisqu’on élève au carré, on peut proposer :
z = (grand(1,1,’norm’,0,1))\^{}2/2}}
5.a. L’algorithme proposé simule ![]() variables
variables ![]() indépendantes de loi exponentielle de paramètre
indépendantes de loi exponentielle de paramètre ![]() , et calcule la moyenne des variables
, et calcule la moyenne des variables ![]() définies par
définies par ![]() . On sait que (d’après la loi faible des grands nombres), cette moyenne s’approche de leur espérance commune
. On sait que (d’après la loi faible des grands nombres), cette moyenne s’approche de leur espérance commune ![]()
Donc pour ![]() grand, s contient une valeur proche de
grand, s contient une valeur proche de ![]() .
.
Or par transfert : ![]()
![]()
![]()
5.b. Par le théorème du transfert et les questions précédentes,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 3 : base orthonormale et algèbre bilinéaire
1. D’après le cours, ![]() est un endomorphisme symétrique de l’espace euclidien
est un endomorphisme symétrique de l’espace euclidien ![]() donc il est diagonalisable et il existe une base orthonormale
donc il est diagonalisable et il existe une base orthonormale ![]() de
de ![]() formée de vecteurs propres de
formée de vecteurs propres de ![]() .
.
2.a. Soit ![]() un vecteur de
un vecteur de ![]()
![]() , décomposition de
, décomposition de ![]() dans
dans ![]() . Notons
. Notons ![]() la valeur propre associée à
la valeur propre associée à ![]() , ainsi pour tout
, ainsi pour tout ![]() de
de ![]() ,
, ![]() .
.
![]()
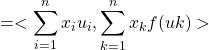
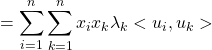 ,par bilinéarité.
,par bilinéarité.
Or ![]() si
si ![]() et
et ![]() sinon. Donc
sinon. Donc ![]() puisque pour tout
puisque pour tout ![]() ,
, ![]() .
.
Donc ![]() .
.
2.b. En reprenant les notations précédentes, ![]()
![]()
![]()
(car ![]() )
)
Donc ![]()
La réciproque est évidente puisque ![]() .
.
Ainsi : ![]() si, et seulement si,
si, et seulement si, ![]()
2.c. ![]() ,
, ![]() et
et ![]() désignent des vecteurs de
désignent des vecteurs de ![]() ,
,![]() un réel.
un réel.
![]() est symétrique car
est symétrique car
![]()
![]() par symétrie de
par symétrie de ![]()
![]()
![]() car
car ![]() est symétrique.
est symétrique.
![]() est linéaire à gauche car
est linéaire à gauche car
![]()
![]()
![]()
Par symétrie, ![]() est aussi linéaire à droite.
est aussi linéaire à droite.
![]() est positive par 2.(a) et définie par 2.(b).
est positive par 2.(a) et définie par 2.(b).
![]() est un produit scalaire sur
est un produit scalaire sur ![]()
3.a. Soit ![]() l’endomorphisme défini par :
l’endomorphisme défini par :
![]()
Pour tout ![]() de
de ![]() ,
,
![]()
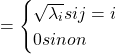
![]()
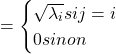
![]()
Ainsi ![]() est symétrique << sur la base
est symétrique << sur la base ![]() >>. Ce résultat s’étend à
>>. Ce résultat s’étend à ![]() par bilinéarité.
par bilinéarité.
![]() est une base orthonormale formée de vecteurs propres de
est une base orthonormale formée de vecteurs propres de ![]() , et que ses valeurs propres sont les
, et que ses valeurs propres sont les ![]() , strictement positives.
, strictement positives.
De plus, pour tout ![]() de
de ![]() ,
, ![]()
![]()
![]() .
.
Les endomorphismes ![]() et
et ![]() coïncident sur la base
coïncident sur la base ![]() , donc ils sont égaux.
, donc ils sont égaux.
Il existe un endomorphisme ![]() , symétrique, tel que
, symétrique, tel que ![]() et
et ![]()
3.b. ![]() n’admet pas
n’admet pas ![]() pour valeur propre,
pour valeur propre, ![]() est injectif. Et comme
est injectif. Et comme ![]() est un endomorphisme d’un espace de dimension finie,
est un endomorphisme d’un espace de dimension finie, ![]() est bijectif.
est bijectif.
3.c. Soit ![]() dans
dans ![]() .
.
![]()
![]()
![]() car
car ![]()
![]() ,
,
![]()
![]() car
car ![]() est symétrique,
est symétrique,
![]()
![]()
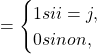 puisque la base canonique est orthonormale pour le produit calaire canonique
puisque la base canonique est orthonormale pour le produit calaire canonique ![]() .
.
Ainsi,![]()

![]() est une base orthonormale pour le produit scalaire
est une base orthonormale pour le produit scalaire ![]()
Problème
Partie 1 : reste d’une série
1. Pour ![]() :
:
![]()
![]() ,
,
or ![]()
Donc ![]()
2.a. Puisque ![]() , nous avons par croissance comparée
, nous avons par croissance comparée ![]()
2.b. ![]() , donc
, donc ![]() en
en ![]() .
.
Comme ![]() est une série de Riemann convergente,
est une série de Riemann convergente, ![]() est convergente.
est convergente.
3.a. 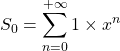 … Il s’agit d’une série géométrique
… Il s’agit d’une série géométrique
Donc : ![]()
3.b. 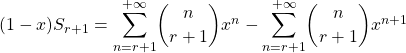

![Rendered by QuickLaTeX.com =x {\displaystyle\sum_{#n=#r}^{\borne{#+\infty}}} [\dbinom {n+1}{r+1} - \dbinom n{r+1}]x^{n}+\dbinom{r}{r+1}x^{r+1}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cefef984f9c93f6b4685e70926fb0787_l3.png)
Or ![]() par la formule de Pascal et
par la formule de Pascal et ![]() , d’où
, d’où ![]()
3.c. Par une itération (on pourrait également le montrer par récurrence) :
![]()
![]()
![]() , ainsi
, ainsi ![Rendered by QuickLaTeX.com \forall x\in ]0;1[, r\in\N, {\displaystyle\sum_{#n=#r}^{\borne{#+\infty}}} \dbinom r{n}x^{n} =\dfrac{x^r}{(1-x)^{r+1}}.](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b9825c1038b73e1c381fd5a5510b4108_l3.png)
3.d. Et en divisant par ![]() (
(![]() ),
),
![Rendered by QuickLaTeX.com \forall x\in ]0;1[, r \in \mathbb{N}, {\displaystyle\sum_{#n=#r}^{\borne{#+\infty}}} \dbinom nrx^{n-r}=\dfrac{1}{(1-x)^{r+1}}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f629e0d9328b8198d63efd75c59daa5a_l3.png)
Partie 2 : loi géométrique
1.a. Comme le joueur peut ne jamais jouer, ![]() .
.
![]() , et pour
, et pour ![]() ,
,
![]() ,
,
D’après la formule des probabilités composées :
![]()
=![]()
![]() , formule encore valable si
, formule encore valable si ![]() .
.
Donc :
![]() ,
,
et ![]()
1.b. Comme ![]() ,
, ![]() , et pour tout
, et pour tout ![]() de
de ![]() ,
, ![]()
![]()
![]() , donc
, donc ![]() suit la loi géométrique de paramètre
suit la loi géométrique de paramètre ![]()
Comme ![]() et
et ![]() , on a, par linéarité,
, on a, par linéarité, ![]() possède une espérance, et
possède une espérance, et ![]()
![]()
1.c. De même, ![]() entraine
entraine ![]() existe et
existe et ![]()
![]()
2.a. ![]() Si
Si ![]() , l’évènement
, l’évènement ![]() entraine
entraine ![]() puisque le joueur ne joue jamais (100\% des gagnants ont tenté leur chance …).
puisque le joueur ne joue jamais (100\% des gagnants ont tenté leur chance …).
Sachant ![]() ,
, ![]() est constante (ou dégénérée), égale à
est constante (ou dégénérée), égale à ![]()
![]() Si
Si ![]() , l’évènement
, l’évènement ![]() entraine que le joueur participe à
entraine que le joueur participe à ![]() partie(s) indépendante(s) avec une même probabilité de succès
partie(s) indépendante(s) avec une même probabilité de succès ![]() . Son nombre de succès
. Son nombre de succès ![]() suit alors la loi binomiale de paramètres
suit alors la loi binomiale de paramètres ![]() et
et ![]() .
.
Sachant ![]() avec
avec ![]() , la loi conditionnelle de
, la loi conditionnelle de ![]() est
est ![]()
2.b. ![]() , et le système complet d’évènements
, et le système complet d’évènements ![]() permet d’écrire, à l’aide de la formule des probabilités totales, pour tout
permet d’écrire, à l’aide de la formule des probabilités totales, pour tout ![]() de
de ![]() ,
, ![Rendered by QuickLaTeX.com P(Y=k)= {\displaystyle\sum_{#n=#0}^{\borne{#+\infty}}} P(X=n)P_{[X=n]}(Y=k)](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-79774c1b6e1eda0f614a4e243fdecfce_l3.png)
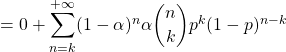
![Rendered by QuickLaTeX.com =\alpha(\dfrac{p}{1-p})^k\times {\displaystyle\sum_{#n=#k}^{\borne{#+\infty}}} \dbinom nk[(1-\alpha)(1-p)]^n](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-30f927f49b840d2e4a493e2914098b33_l3.png) , soit, en reconnaissant
, soit, en reconnaissant ![]() de la partie 1 avec
de la partie 1 avec ![]() ,
,
![]()
![]()
![]()
Soit ![]() .
.
Alors ![]()
![]()
Ainsi : ![]() , et,
, et, ![]() avec
avec ![]()
3. En s’inspirant de la démarche de 1.(b), ![]() suit la loi géométrique de paramètre
suit la loi géométrique de paramètre ![]() ,
, ![]() existe et vaut
existe et vaut ![]()
Et de même, ![]()
![]()
![]()
4.a. Le joueur gagnant ![]() parties et en perdant
parties et en perdant ![]() ,
, ![]()
4.b. Par linéarité, ![]()
![]()
![]()
4.c.
![]() Soit
Soit ![]() . Sachant
. Sachant ![]() ,
, ![]() suit
suit ![]() donc
donc ![]() existe et vaut
existe et vaut ![]() . Par linéarité,
. Par linéarité, ![]() existe et vaut
existe et vaut ![]() puisque
puisque ![]() .
.
Notons que, pour ![]() , on a encore
, on a encore ![]()
![]()
![]()
![]() est le terme général d’une série convergente puisque
est le terme général d’une série convergente puisque ![]() admet un moment d’ordre
admet un moment d’ordre ![]()
![]() D’après le théorème de l’espérance totale, avec le système complet d’évènements
D’après le théorème de l’espérance totale, avec le système complet d’évènements ![]() ,
, ![]() possède une espérance et
possède une espérance et ![Rendered by QuickLaTeX.com \mathbb{E}(XY)= {\displaystyle\sum_{#n=#0}^{\borne{#+\infty}}} P(X=n)\E(XY|[X=n]).](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4642e10199933781619a2a22e390d305_l3.png)
Par transfert

![]()
![]()
![]()
![]() , d’où
, d’où
![]() existe et vaut
existe et vaut ![]()
4.d. ![]()
![]() , et
, et ![]()
![]()
![]()
![]()
![]()
![]()
5.a. alpha = input(‘entrez la valeur de alpha :’)
p = input(‘entrez la valeur de p :’)
X = grand(1,1,’geom’,alpha) – 1
Y = grand(1,1,’bin’,X,p)
disp(X) ; disp(Y)
5.b. Que l’on peut compléter par :
G = 2*Y – X
disp(G)

