Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EDHEC Maths ECS 2016
Revenir à tous les corrigés des annales maths BCE
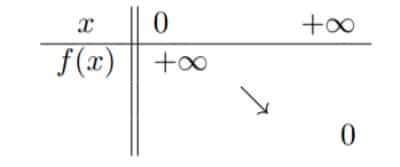
Exercice 1 : Scilab, dérivation et variation de suite
1/ a/ La fonction ![]() est dérivable sur
est dérivable sur ![]() comme quotient de deux fonctions dérivables dont le dénominateur ne s’annule pas sur
comme quotient de deux fonctions dérivables dont le dénominateur ne s’annule pas sur ![]() , et on a :
, et on a :
![]() sur
sur ![]()
Donc la fonction ![]() est strictement décroissante sur
est strictement décroissante sur ![]() .
.
De plus, ![]() et
et ![]() (pas des formes indéterminées)
(pas des formes indéterminées)
b/ Par récurrence immédiate de la propriété
![]() est bien défini et
est bien défini et ![]()
function y=f(x,n)
if x==1 then y=n
else y=(1-x^(n+1))/(1-x)-1
endfunction
2/ Les script calculent les termes successifs de la suite, mais le premier script s’arrête lorsque u<=0.00001 et le second lorsque u>=100000, n sert de compteur, il indique l’indice du dernier terme calculé.
Conclusion : ![]() et
et ![]() et ce sont les premiers termes de la suite à vérifier ces inégalités.
et ce sont les premiers termes de la suite à vérifier ces inégalités.
De telles écarts peuvent nous faire conjecturer que la suite n’admet pas de limite (et même que la suite des termes de rang pair tend vers ![]() et celle des termes de rang impair tend vers
et celle des termes de rang impair tend vers ![]() ).
).
3/ a/ ![]() est évidemment dérivable sur
est évidemment dérivable sur ![]() et
et ![]() sur
sur ![]() .
.
La fonction ![]() est donc continue et strictement décroissante sur
est donc continue et strictement décroissante sur ![]() , elle réalise alors une bijection de
, elle réalise alors une bijection de ![]() sur
sur ![]()
b/ Sur ![]() ,
, ![]() ssi
ssi ![]()
ssi ![]() ssi
ssi ![]() .
.
Or d’après la question précédente ![]() possède un unique antécédent dans
possède un unique antécédent dans ![]() par
par ![]() . On le note alors
. On le note alors ![]() .
.
c/ Déterminons le signe de ![]() et
et ![]() :
:
On a : ![]() ,
,
or ![]()
donc par croissance de la fonction exponentielle ![]() ,
,
donc en inversant ![]()
et donc ![]() .
.
Plus simplement, ![]() , puisque
, puisque ![]() .
.
En conclusion : ![]() , or comme
, or comme ![]() est strictement décroissante
est strictement décroissante
on a donc : ![]() .
.
4/ a/ On peut calculer : ![]() ,
, ![]() et
et
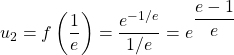 .
.
Or pour cette dernière, ![]() donc
donc ![]()
et on a alors bien ![]() donc
donc ![]() .
.
Pour l’autre inégalité, il suffit de remarquer que ![]() est décroissante de :
est décroissante de : ![]() on tire
on tire
![]() soit
soit ![]()
b/ Montrons que ![]() est croissante. Pour cela, on peut montrer par récurrence que, pour tout
est croissante. Pour cela, on peut montrer par récurrence que, pour tout ![]() :
:
![]()
L’initialisation a été faite en (a).
Supposons que ![]() pour un certain rang
pour un certain rang ![]() fixé, on a alors en composant par
fixé, on a alors en composant par ![]() (décroissante) :
(décroissante) :
![]()
et en composant encore une fois par ![]() (décroissante) :
(décroissante) :
![]()
La propriété est alors initialisée pour ![]() et elle est héréditaire, elle est donc vraie pour tout
et elle est héréditaire, elle est donc vraie pour tout ![]() .
.
Conclusion : ![]() est croissante.
est croissante.
Pour ![]() c’est plus simple : comme
c’est plus simple : comme ![]() est croissante on a pour tout
est croissante on a pour tout ![]() :
:
![]()
en composant par ![]() (décroissante), on a alors, pour tout
(décroissante), on a alors, pour tout ![]() :
:
![]()
et ![]() est alors bien décroissante.
est alors bien décroissante.
5/ a/ Pour ![]() ,
,
![]()
= 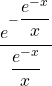
= 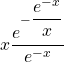
= ![]()
= ![]()
De plus, d’après la question 1., on a : ![]() et
et ![]() ,
,
donc par composition de limite : ![]() ,
,
donc ![]() est bien continue en
est bien continue en ![]() .
.
b/ Soit ![]() . On a :
. On a :
![]() ssi
ssi ![]()
ssi ![]()
L’équation ![]() n’admet donc que deux solutions sur
n’admet donc que deux solutions sur ![]() :
: ![]() et
et ![]() .
.
c/ ![]() est décroissante et minorée (par
est décroissante et minorée (par ![]() ) donc elle converge vers une limite
) donc elle converge vers une limite ![]() (d’après la question 3.(c)),
(d’après la question 3.(c)),
de plus ![]() , donc
, donc ![]() vérifie
vérifie ![]() .
.
Donc, compte tenu de ce qui précède et du fait que ![]() on a nécessairement
on a nécessairement ![]() .
.
d/ Si ![]() alors grâce à
alors grâce à ![]() continue sur
continue sur ![]() ,
,
on aurait ![]() , ou encore
, ou encore ![]() , d’après la question précédente.
, d’après la question précédente.
Ceci est absurde puisque ![]() n’a pas d’antécédent par
n’a pas d’antécédent par ![]() d’après la question 1.(a).
d’après la question 1.(a).
Conclusion : ![]() diverge, de plus, étant croissante, sa limite ne peut être que
diverge, de plus, étant croissante, sa limite ne peut être que ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Algèbre linéaire
1/ a/ ![]() et
et ![]() commutent, donc :
commutent, donc :
![]()
![]()
![]()
b/ D’après la question précédente, ![]() donc pour tout
donc pour tout ![]() , on a :
, on a :
![]()
soit : ![]()
c/ ![]()
donc, pour tout ![]() ,
, ![]() .
.
De plus, ![]() .
.
Donc, avec (b), tout vecteur ![]() de
de ![]() peut s’écrire comme somme d’un vecteur de
peut s’écrire comme somme d’un vecteur de ![]() et d’un vecteur de
et d’un vecteur de ![]() ,
,
on a alors ![]() .
.
Reste à montrer que ![]() pour avoir une somme directe :
pour avoir une somme directe :
Si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() et
et ![]() .
.
Développons alors ![]() , cela revient à :
, cela revient à : ![]() que l’on applique à
que l’on applique à ![]() pour obtenir :
pour obtenir :
![]()
Soit :
![]()
Conclusion : ![]()
2/ a/ On peut poser ![]() , puis on trouve en identifiant :
, puis on trouve en identifiant : ![]() et
et ![]() .
.
Conclusion : ![]() .
.
b/ Comme dans la question 1., on a cette fois-ci à partir de ![]()
![]()
Donc, pour tout ![]() :
:
![]()
Or l’énoncé nous dit que : ![]() ,
,
donc ![]()
de plus ![]() .
.
Donc ![]() .
.
De plus, de ![]() on a
on a ![]() est annulateur de
est annulateur de ![]()
et comme dans la question 1., si ![]()
alors ![]()
soit ![]() ,
,
donc ![]() .
.
3/ a/ ![]() , il existe donc
, il existe donc ![]() tels que
tels que ![]() .
.
De plus ![]() et
et ![]() .
.
Donc d’après l’énoncé, ![]() et
et ![]() .
.
b/ Si ![]() , comme précédemment, il existe
, comme précédemment, il existe ![]() tel que
tel que
![]() et
et ![]()
(remarque : et plus généralement ![]() pour tout entier
pour tout entier ![]() ).
).
![]() étant annulateur de
étant annulateur de ![]() , on a
, on a ![]() ,
,
soit : ![]()
et donc d’après la remarque précédente :
![]() .
.
Or, ![]() donc
donc ![]() .
.
Conclusion : ![]() .
.
De plus ![]() , donc
, donc ![]() ou encore :
ou encore :
![]()
On a aussi :
![]()
![]()
![]() .
.
Donc pour tout ![]() :
:
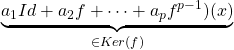
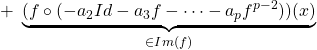
![]()
Donc ![]() et avec ce qui précède :
et avec ce qui précède : ![]() .
.
c/ C’est plutôt clair, avec dans la question 1. ![]()
et dans la question 2. ![]()
qui vérifient bien ![]() et
et ![]() .
.
Exercice 3 : fonction à 2 variables et matrice hessienne
1/ a/ On a :

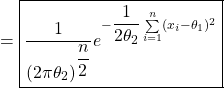
Donc :
![]()
= 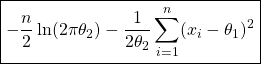
2/ a/ ![]() est bien de classe
est bien de classe ![]() , par la somme de la composée et de quotient de fonctions de classe
, par la somme de la composée et de quotient de fonctions de classe ![]() (polynômes) dont le dénominateur ne s’annule pas sur
(polynômes) dont le dénominateur ne s’annule pas sur ![]() et de la composée de la fonction
et de la composée de la fonction ![]() qui est bien
qui est bien ![]() sur
sur ![]() .
.
b/ On a :
 et :
et :
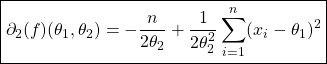
On cherche les points critiques donc :
![Rendered by QuickLaTeX.com \left\{ \begin{array}{l} \partial_1(f)(\theta_1,\theta_2)=0\\[7mm] \partial_2(f)(\theta_1,\theta_2)=0 \end{array} \right.](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6c2300b47ffba7a28a7de68335b64644_l3.png)
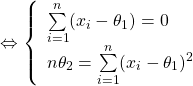
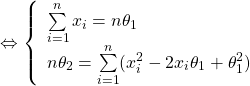
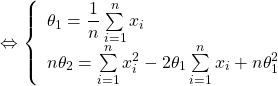
Or, d’après la première ligne ![]() donc en remplaçant dans la deuxième ligne, on a :
donc en remplaçant dans la deuxième ligne, on a :
![Rendered by QuickLaTeX.com \left\{ \begin{array}{l} \partial_1(f)(\theta_1,\theta_2)=0\\[7mm] \partial_2(f)(\theta_1,\theta_2)=0 \end{array} \right.](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6c2300b47ffba7a28a7de68335b64644_l3.png)
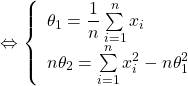
On remarque alors que ![]() est uniquement déterminé par les
est uniquement déterminé par les ![]()
et ![]() est lui aussi uniquement déterminé par les
est lui aussi uniquement déterminé par les ![]() et
et ![]() (qui est unique).
(qui est unique).
Conclusion : ![]() admet un unique point critique
admet un unique point critique ![]() sur
sur ![]() et
et ![]() vérifie :
vérifie :
![]() et
et ![]()
c/ Calculons les dérivées partielles d’ordre 2 de ![]() :
:
![]() ;
;
![]()
et ![]()
Donc en ![]() , avec par définition
, avec par définition
![]() et
et ![]()
(voir la question 2.(b)), on a :
![]()
![]()
et
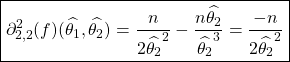
d/ La matrice hessienne de ![]() en
en ![]() est donc diagonale et ses valeurs propres :
est donc diagonale et ses valeurs propres : ![]() et
et ![]() sont strictement négatives,
sont strictement négatives, ![]() admet donc un maximum local en
admet donc un maximum local en ![]() .
.
e/ ![]() admet donc un maximum local en
admet donc un maximum local en ![]() signifie qu’il existe un voisinage
signifie qu’il existe un voisinage ![]() de
de ![]() tel que
tel que
![]()
![]() ,
,
or ![]() et la fonction exponentielle étant croissante, on a
et la fonction exponentielle étant croissante, on a
![]()
![]() .
.
Conclusion : ![]() admet bien un maximum local en
admet bien un maximum local en ![]() .
.
3/ On a :
![]()
![]()
![]()
![]() .
.
Donc ![]() est bien un estimateur sans biais de
est bien un estimateur sans biais de ![]() .
.
4/ Rappelons que pour tout ![]() ,
, ![]() .
.
On a alors :
![]()
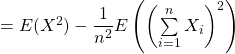
Or, ![]()
donc : 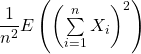
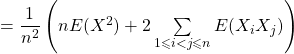
mais par indépendance avec ![]() :
: ![]() donc :
donc :
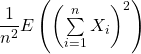
![]()
La dernière somme compte ![]() termes,
termes,
donc : 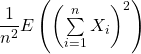
![]()
![]()
En revenant à ![]() on a alors :
on a alors :
![]()
![]()
Conclusion : ![]() est un estimateur asymptotiquement sans biais de
est un estimateur asymptotiquement sans biais de ![]() .
.
5/ a/ ![]() étant un estimateur sans biais de
étant un estimateur sans biais de ![]() , il suffit, pour qu’il soit convergent, que
, il suffit, pour qu’il soit convergent, que ![]() .
.
Or, on a : ![]() , donc
, donc ![]() converge bien en probabilité vers
converge bien en probabilité vers ![]() .
.
Puisque la fonction réelle ![]() est continue, on peut en déduire que la suite
est continue, on peut en déduire que la suite ![]() converge en probabilité vers
converge en probabilité vers ![]() .
.
b/ On a la loi de ![]() , une densité de
, une densité de ![]() est
est ![]() .
.
Pour que ![]() possède un moment d’ordre 4 il faut que l’intégrale
possède un moment d’ordre 4 il faut que l’intégrale ![]() soit absolument convergente (ou tout simplement converge, l’intégrale étant positive).
soit absolument convergente (ou tout simplement converge, l’intégrale étant positive).
Or, par croissance comparée, ![]() ,
,
donc ![]() ,
,
donc ![]() et
et ![]() convergent et
convergent et ![]() admet bien un moment d’ordre 4.
admet bien un moment d’ordre 4.
Par conséquent ![]() admet un moment d’ordre 2, on peut donc utiliser la loi faible des grands nombres avec
admet un moment d’ordre 2, on peut donc utiliser la loi faible des grands nombres avec ![]() (Koenig-Huygens) :
(Koenig-Huygens) :
![]() converge en probabilité vers
converge en probabilité vers ![]()
c/ ![]()
soit encore en ajoutant et retranchant ![]() :
:
![]()
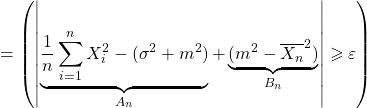
Or, si ![]() alors
alors ![]() ou
ou ![]() ,
,
car sinon, par inégalité triangulaire :
![]()
Donc :
![]()
et ![]()
Ce qu’il fallait démontrer.
5/ d/ Il suffit pour cela de montrer que ![]() converge en probabilité vers
converge en probabilité vers ![]() . Or, pour tout
. Or, pour tout ![]() , on a :
, on a :
![]()
![]()
mais, d’après la question 5. (b), ![]() converge en probabilité vers
converge en probabilité vers ![]()
ce qui revient à ![]()
et, d’après la question 5. (a), ![]() converge en probabilité vers
converge en probabilité vers ![]()
ce qui revient à ![]() .
.
On a alors bien :
![]()
et ![]() est bien un estimateur convergent de
est bien un estimateur convergent de ![]() .
.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Problème : Algèbre linéaire et probabilité avec les chaines de Markov
Partie 1 : Résultats préliminaires
1/ Pour tout ![]() et tout
et tout ![]() , le coefficient situé à l’intersection de la
, le coefficient situé à l’intersection de la ![]() ligne et de la
ligne et de la ![]() colonne de
colonne de ![]() est donné par :
est donné par :
![]() et par somme finie de limites, on a :
et par somme finie de limites, on a :
![]()
qui n’est rien d’autre que le coefficient situé à l’intersection de la ![]() ligne et de la
ligne et de la ![]() colonne de
colonne de ![]() .
.
Conclusion : on a donc bien ![]() .
.
2/ En considérant la matrice colonne
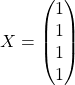 , on a dans ce cas
, on a dans ce cas ![]() .
.
![]() est donc bien une valeur propre de
est donc bien une valeur propre de ![]() .
.
3/ On utilise le résultat bien connu : pour toutes matrices ![]() et
et ![]() de
de ![]() ,
, ![]() que l’on redémontre ici :
que l’on redémontre ici :
![]()
![]()
![]()
Or, si ![]() est diagonalisable il existe une matrice diagonale
est diagonalisable il existe une matrice diagonale ![]() constituées des valeurs propres de
constituées des valeurs propres de ![]() et une matrice inversible
et une matrice inversible ![]() telles que :
telles que : ![]() . On a alors :
. On a alors :
![]()
![]()
![]() d’après le résultat redémontré précédemment.
d’après le résultat redémontré précédemment.
Conclusion : Si ![]() est diagonalisable alors
est diagonalisable alors ![]() est égal à la somme de ses valeurs propres.
est égal à la somme de ses valeurs propres.
Partie 2 : Étude de la matrice d’une chaîne de Markov
4/Tout d’abord, il faut remarquer que, les tirages étant des échanges, il y a toujours 3 boules dans chaque urnes.
De plus, si l’urne ![]() contient
contient ![]() boules blanches alors elle contient aussi
boules blanches alors elle contient aussi ![]() boules noires et dans ce cas l’urne
boules noires et dans ce cas l’urne ![]() contient
contient ![]() boules noires et
boules noires et ![]() boules blanches.
boules blanches.
- Si l’urne
 contient
contient  boule blanche alors un échange donnera nécessairement
boule blanche alors un échange donnera nécessairement  boules blanche dans l’urne
boules blanche dans l’urne  .
.
Donc : .
. - Si l’urne
 contient
contient  boule blanche alors un échange donnera nécessairement
boule blanche alors un échange donnera nécessairement  boules blanche dans l’urne
boules blanche dans l’urne  .
.
Donc : .
. - Dans les autres cas, si l’urne
 contient
contient  boules blanches alors au prochain tirage elle ne pourra en contenir que
boules blanches alors au prochain tirage elle ne pourra en contenir que  ,
,  ou
ou  .
.
Pour rester avec le même nombre ![]() de boules dans
de boules dans ![]() , il faut choisir une boule noire dans
, il faut choisir une boule noire dans ![]() et une boule noire dans
et une boule noire dans ![]() ou alors il faut choisir une boule blanche dans
ou alors il faut choisir une boule blanche dans ![]() et une boule blanche dans
et une boule blanche dans ![]() .
.
On a donc : ![]()
Soit : ![]()
Pour augmenter le nombre de boules blanches d’une unité il faut choisir une boule noire dans ![]() et une boule blanche dans
et une boule blanche dans ![]() .
.
Donc : 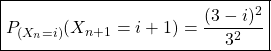
Pour diminuer le nombre de boules blanches d’une unité il faut choisir une boule blanche dans ![]() et une boule noire dans
et une boule noire dans ![]() .
.
Donc : 
5/ a/ La matrice ![]() est donnée par :
est donnée par :

Soit, d’après la question précédente :
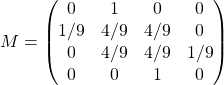
qui est bien la matrice donnée à la question 12.
b/ Pour tout ![]() , d’après la formule des probabilités totales avec le système complet d’événements
, d’après la formule des probabilités totales avec le système complet d’événements ![]() , on a :
, on a :
![]()
![]()
![]()
![]()
L’égalité demandée est donc vraie pour le ![]() coefficient de
coefficient de ![]() .
.
Or, ceci étant vrai pour tout ![]() , on bien :
, on bien :
Pour tout entier ![]() admis pour
admis pour ![]() et 2
et 2
c/ Par une récurrence immédiate
6/ a/ La somme des coefficients d’une ligne de ![]() vaut toujours 1, donc d’après la question 2., 1 est valeur propre de
vaut toujours 1, donc d’après la question 2., 1 est valeur propre de ![]() .
.
b/ Un simple calcul donne :
![]()
et ![]()
Donc ![]() est bien un vecteur propre de
est bien un vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() et
et ![]() est bien un vecteur propre de
est bien un vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() .
.
c/ Si ![]() est diagonalisable alors, d’après la question 3., la somme des valeurs propres de
est diagonalisable alors, d’après la question 3., la somme des valeurs propres de ![]() doit être égale à
doit être égale à ![]() .
.
On a déjà 3 valeurs propres de ![]() , la dernière
, la dernière ![]() vérifie donc :
vérifie donc :
![]() et donc
et donc ![]() .
.
Montrons que ![]() n’est pas inversible ou, ce qui revient au même, montrons que
n’est pas inversible ou, ce qui revient au même, montrons que ![]() n’est pas inversible :
n’est pas inversible :
On a :
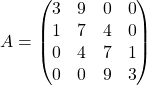 .
.
Les étapes successives suivantes :
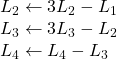
donnent la matrice :

qui n’est pas inversible, donc ![]() n’est pas inversible.
n’est pas inversible.
Conclusion : ![]() est bien valeur propre de
est bien valeur propre de ![]() qui possède alors 4 valeurs propres distinctes et est donc bien diagonalisable.
qui possède alors 4 valeurs propres distinctes et est donc bien diagonalisable.
Remarque : pour montrer que ![]() n’est pas inversible, on aurait pu aussi montrer que :
n’est pas inversible, on aurait pu aussi montrer que : ![]()
Partie 3 : Recherche d’une loi stationnaire
7/ D’après la question précédente, ![]() est diagonalisable.
est diagonalisable.
De plus un vecteur propre associé à la valeur propre ![]() est le vecteur ne contenant que des « 1 » (voir la question 2.).
est le vecteur ne contenant que des « 1 » (voir la question 2.).
Il existe donc une matrice inversible ![]() (constituée de vecteurs propres dont le premier peut être le vecteur propre ne contenant que des « 1 ») et une matrice diagonale
(constituée de vecteurs propres dont le premier peut être le vecteur propre ne contenant que des « 1 ») et une matrice diagonale ![]() telles que
telles que ![]() .
.
8/ Une récurrence immédiate montre que, pour tout ![]() ,
, ![]() .
.
Or, ![]() étant diagonale, on a
étant diagonale, on a ![]()
De plus ![]()
![]()
![]()
donc ![]() et d’après les résultats admis dans les préliminaires :
et d’après les résultats admis dans les préliminaires :
![]()
9/ a/ De ![]() on tire
on tire ![]() , soit :
, soit :
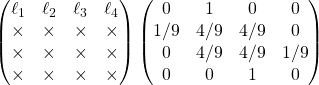
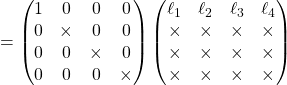
En identifiant chaque coefficient de la première ligne du résultat de ces produits, on obtient alors :
![Rendered by QuickLaTeX.com \left\{ \begin{array}{lllll} & \dfrac{1}{9}\times\ell_2 & & & = \ell_1\\ \ell_1 & + \dfrac{4}{9}\ell_2 & + \dfrac{4}{9}\ell_3 & & = \ell_2\\[2mm] & \dfrac{4}{9}\ell_2 & + \dfrac{4}{9}\ell_3 & + \ell_4 & = \ell_3\\ & & \dfrac{1}{9}\ell_3 & & = \ell_4 \end{array} \right.](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3df2f18a45ad04ebb6acf1150bbdf451_l3.png)
De ![]() et
et ![]() on tire :
on tire : ![]() et
et ![]()
et de ![]()
et on a alors bien :
![]() et
et ![]()
b/ On a ![]() et d’après la question 7., la première colonne de
et d’après la question 7., la première colonne de ![]() ne contient que des « 1 », donc :
ne contient que des « 1 », donc :

On a donc : ![]() , mais comme
, mais comme ![]() et
et ![]() cela revient alors à :
cela revient alors à : ![]() donc :
donc :
![]()
10/ ![]()
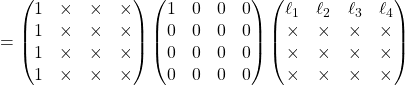
Soit :
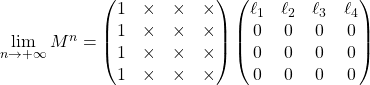
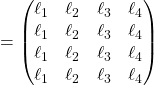
Or, ![]() et
et ![]() , donc :
, donc :
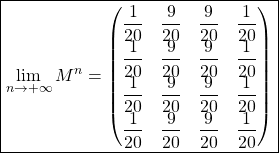
11/ a/ Tout d’abord, on a : ![]() . Utilisons les événements suggérés par l’énoncé :
. Utilisons les événements suggérés par l’énoncé :
![]() ,
,
donc par la formule des probabilités composées :
![]()
![]()
![]() .
.
De même : ![]()
![]()
et par incompatibilité et par la formule des probabilités composées :
![]()
![]()
![]()
![]() .
.
Pour ![]() , on trouve alors
, on trouve alors ![]() et
et
![]()
![]()
![]() .
.
Conclusion : la loi de ![]() est donnée par :
est donnée par : ![]()
![]()
b/ On a :
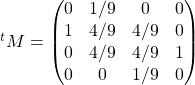
et
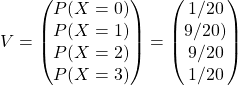 .
.
Un simple calcul donne : ![]() ,
, ![]() est donc bien un vecteur propre de
est donc bien un vecteur propre de ![]() associé à la valeur propre 1.
associé à la valeur propre 1.
c/ Pour cela il suffit de montrer que : ![]() .
.
Or, d’après la question 5.(c), on a, pour tout ![]() ;
;
![]() , avec
, avec ![]()
et grâce aux résultats admis dans les préliminaires,
![]()
mais d’après la question 10., 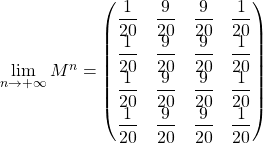
un simple calcul montrer alors bien que ![]() .
.
Conclusion : la suite X_n converge alors bien en loi vers X.
d/ Le programme renvoie la suite des ![]() premiers états suivants l’état initial
premiers états suivants l’état initial ![]() (pour avoir des valeurs comprises entre 1 et 4, puis on soustrait 1 à chaque coefficient du vecteur renvoyé).
(pour avoir des valeurs comprises entre 1 et 4, puis on soustrait 1 à chaque coefficient du vecteur renvoyé).
Autrement dit, le programme simule l’expérience et donne le nombre de boules blanches dans l’urne ![]() lors des
lors des ![]() premiers tirages.
premiers tirages.
Ensuite, le programme calcule la moyenne des nombres d’états où ![]() (l’urne
(l’urne ![]() n’a pas de boule blanche),
n’a pas de boule blanche),
on peut donc supposer que ![]() sera proche de
sera proche de ![]() lorsque
lorsque ![]() est assez grand.
est assez grand.

