Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EDHEC Maths ECS 2017
Revenir à tous les corrigés des annales maths BCE
Exercice 1 : Scilab et variation de suite
1/ a/ On peut compléter le programme comme suit :
function y=f(x,n)
y=sum(x.^(1:n))
endfunction
b/ Pour ![]() , on a :
, on a : ![]() et pour
et pour ![]() ,
, ![]() . Le programme peut alors s’écrire :
. Le programme peut alors s’écrire :
function y=f(x,n)
if x==1 then y=n
else y=(1-x^(n+1))/(1-x)-1
endfunction
2/ ![]() est continue et dérivable (c’est un polynôme) et sa dérivée, donnée par l’expression
est continue et dérivable (c’est un polynôme) et sa dérivée, donnée par l’expression ![]() , est strictement positive sur
, est strictement positive sur ![]() .
. ![]() réalise donc une bijection croissante de
réalise donc une bijection croissante de ![]() sur
sur ![]() . Le nombre
. Le nombre ![]() possède donc un unique antécédent dans
possède donc un unique antécédent dans ![]() par
par ![]() .
.
Conclusion : Pour tout ![]() , l’équation
, l’équation ![]() possède une unique solution
possède une unique solution ![]() dans
dans ![]()
3/ a/ Pour tout ![]() , on a :
, on a :
![Rendered by QuickLaTeX.com \[f_{n+1}(\alpha_n)=\sum\limits_{k=1}^{n+1}\alpha_n^k=f_n(\alpha_n)+\alpha_n^{n+1}=1+\alpha_n^{n+1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b6ddce69cb1852e268c32aeaeca52749_l3.png)
Or, ![]() , donc
, donc ![]() .
.
On a donc, pour tout ![]() ,
,
![]()
et comme ![]() est strictement croissante, on peut alors conclure que :
est strictement croissante, on peut alors conclure que : ![]() .
.
Conclusion : La suite ![]() est décroissante.
est décroissante.
b/ La suite ![]() est décroissante et minorée par
est décroissante et minorée par ![]() .
.
Conclusion : La suite ![]() converge vers une limite
converge vers une limite ![]() .
.
4/ a/ Par définition, ![]() est l’unique solution de l’équation
est l’unique solution de l’équation ![]() dans
dans ![]() . Un simple calcul de discriminant donne alors
. Un simple calcul de discriminant donne alors ![]() . De plus
. De plus ![]() donne directement les inégalités demandées.
donne directement les inégalités demandées.
Conclusion : ![]() et on a bien
et on a bien ![]() .
.
4/ b/ ![]() étant décroissante, on a pour tout entier
étant décroissante, on a pour tout entier ![]() :
:
![]()
![]()
Or, puisque
Conclusion : ![]() .
.
4/ c/ D’après 1.(b), ![]() est l’unique solution, dans
est l’unique solution, dans ![]() , de l’équation
, de l’équation ![]() . Donc, pour tout
. Donc, pour tout ![]() :
:
![]()
Or, d’après les questions précédentes,
![]()
La limite
Conclusion : ![]() .
.
5/ Fixons ![]() . On sait déjà que
. On sait déjà que ![]() est croissante sur
est croissante sur ![]() et
et ![]() . Le programme va alors tester toutes les valeurs de
. Le programme va alors tester toutes les valeurs de ![]() à partir de
à partir de ![]() et avec un pas de 0,001 tant que
et avec un pas de 0,001 tant que ![]() . La valeur affichée par le programme est alors le premier de ces nombres pour lequel
. La valeur affichée par le programme est alors le premier de ces nombres pour lequel ![]() . Le résultat affiché est donc le plus petit nombre du type
. Le résultat affiché est donc le plus petit nombre du type ![]() (
(![]() ) supérieur ou égal à
) supérieur ou égal à ![]() .
.
Conclusion : Le résultat affiché est donc une valeur approchée par excès à 0,001 près de ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Variable aléatoire et fonction de répartition
1/ a/ Soit ![]() . Par indépendance des variables
. Par indépendance des variables ![]() , on a :
, on a :
![Rendered by QuickLaTeX.com \[F_{M_n}(x)=P\left(\bigcap\limits_{i=1}^{n}(X_i\leqslant x)\right)=\prod\limits_{i=1}^{n}P(X_i\leqslant x)=\left\{\begin{array}{ll}0 & \mbox{, si } x<0\\x^n & \mbox{, si } 0\leqslant x\leqslant 1\\1 & \mbox{, si } x> 1\\\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-315d60d57522583bcd5de0faad0f03a7_l3.png)
Les limites à gauches et à droites de la fonction de répartition
Conclusion : ![]() est une variable à densité et sa fonction de répartition est définie pour tout
est une variable à densité et sa fonction de répartition est définie pour tout ![]() par
par 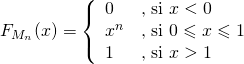
1/ b/ Une densité de ![]() est alors obtenue en dérivant
est alors obtenue en dérivant ![]() là où elle est dérivable et en prenant des valeurs arbitraires en
là où elle est dérivable et en prenant des valeurs arbitraires en ![]() et en
et en ![]() .
.
Conclusion : Une densité ![]() de
de ![]() est définie pour tout
est définie pour tout ![]() par :
par : 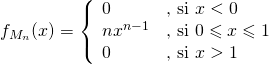
1/ c/ Les intégrales suivantes sont absolument convergentes :
![]()
car ![]() est nulle en dehors de
est nulle en dehors de ![]() et les intégrandes sont continues sur le segment
et les intégrandes sont continues sur le segment ![]() .
. ![]() et
et ![]() admettent donc bien une espérance que l’on calcule :
admettent donc bien une espérance que l’on calcule :
![]()
![]()
Conclusion : ![]() et
et ![]() admettent donc bien une espérance,
admettent donc bien une espérance, ![]() et
et ![]()
1/ d/ ![]() admettant un moment d’ordre 2,
admettant un moment d’ordre 2, ![]() admet une espérance et est positive, on peut donc appliquer l’inégalité de Markov à
admet une espérance et est positive, on peut donc appliquer l’inégalité de Markov à ![]() :
:
![]()
Or, par linéarité de l’espérance,
![]()
Conclusion : ![]()
1/ e/ Pour tout ![]() ,
, ![]() , donc par encadrement
, donc par encadrement
![]()
Conclusion : ![]() et ce résultat signifie que la suite
et ce résultat signifie que la suite ![]() converge en probabilité vers la variable certaine égale à 1.
converge en probabilité vers la variable certaine égale à 1.
2/ a/ Dans le programme proposé, X est une réalisation de ![]() variables indépendantes de loi uniforme sur
variables indépendantes de loi uniforme sur ![]() .
. ![]() peut alors être simulée à l’aide de la fonction max :
peut alors être simulée à l’aide de la fonction max :
function Y=f(n)
X = grand(1,n,’unf’,0,1)
Y = n*(1-max(X))
endfunction
2/ b/ Les deux histogrammes sont très proches, les simulations de ![]() sont donc prochent des simulations d’une loi exponentielle de paramètre 1.
sont donc prochent des simulations d’une loi exponentielle de paramètre 1.
Conclusion : On peut conjecturer que ![]() converge en loi vers une variable de loi exponentielle de paramètre 1.
converge en loi vers une variable de loi exponentielle de paramètre 1.
3/ a/ Pour tout ![]() ,
,
![]()
La dernière égalité étant vraie car ![]() est à densité.
est à densité.
Et avec 1.(a), on conclut :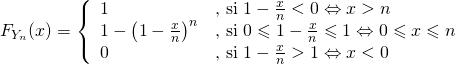
3/ b/ Soit ![]() . Pour
. Pour ![]() , on a d’après 3.(a),
, on a d’après 3.(a),
![]()
Or, ![]() . En effet,
. En effet, ![]() , donc
, donc ![]() , ou encore
, ou encore ![]() . Reste alors à utiliser la continuité de la fonction exponentielle pour obtenir ce qui était annoncé.
. Reste alors à utiliser la continuité de la fonction exponentielle pour obtenir ce qui était annoncé.
Conclusion : Pour tout ![]() ,
, ![]() .
.
3/ c/ Pour tout ![]() ,
, ![]() et avec 3.(b), on peut conclure que pour tout
et avec 3.(b), on peut conclure que pour tout ![]() ,
, ![]() tend, quand
tend, quand ![]() , vers la fonction de répartition d’une loi exponentielle de paramètre 1.
, vers la fonction de répartition d’une loi exponentielle de paramètre 1.
Conclusion : ![]() converge en loi vers une variable de loi exponentielle de paramètre 1.
converge en loi vers une variable de loi exponentielle de paramètre 1.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 3 : Norme et algèbre bilinéaire
1/ a/ On a évidemment ![]() et donc, puisque
et donc, puisque ![]() et
et ![]() commutent :
commutent :
![]()
Or, un calcul simple donne : ![]() . Donc :
. Donc :
![]()
Conclusion : ![]() et
et ![]()
1/ b/ Avec ce qui précède, on a :
![]()
Donc :
![]()
Et ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]() et les valeurs propres possibles de
et les valeurs propres possibles de ![]() sont les racines de
sont les racines de ![]() .
.
Conclusion : Un polynôme annulateur de ![]() est
est ![]() et les valeurs propres possibles de
et les valeurs propres possibles de ![]() sont
sont ![]() et
et ![]() .
.
1/ c/ ![]() n’est pas une valeur propre possible.
n’est pas une valeur propre possible.
Conclusion : ![]() est inversible.
est inversible.
2/ On a : 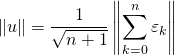 et
et ![]() étant orthonormale,
étant orthonormale,  .
.
Conclusion : ![]() est unitaire :
est unitaire : ![]() .
.
3/ a/ Soit ![]() . Par linéarité du produit scalaire et
. Par linéarité du produit scalaire et ![]() étant orthonormale,
étant orthonormale,
![Rendered by QuickLaTeX.com \[\langle\varepsilon_i,u\rangle=\frac{1}{\sqrt{n+1}}\sum\limits_{k=0}^n\langle\varepsilon_i,\varepsilon_k\rangle=\frac{1}{\sqrt{n+1}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a2e35c0e506ca033dec1f4ec6a3ca61b_l3.png)
Donc,
![Rendered by QuickLaTeX.com \[\|e_i\|=\sqrt{\frac{n+1}{n}}\left\|\varepsilon_i - \frac{1}{\sqrt{n+1}}u\right\|=\sqrt{\frac{n+1}{n}}\left\|\varepsilon_i - \frac{1}{n+1}\sum\limits_{k=0}^n\varepsilon_k\right\|\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b8b93666a4053f12da5a535ab112d307_l3.png)
Ou encore :
![Rendered by QuickLaTeX.com \[\|e_i\|=\sqrt{\frac{n+1}{n}}\left\|\frac{n}{n+1}\varepsilon_i - \frac{1}{n+1}\sum\limits_{\substack{0\leqslant k\leqslant n\\ k\neq i}}\varepsilon_k\right\|\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-24f5ee9da8b19df88ebb62bda7cae922_l3.png)
et toujours avec ![]() orthonormale,
orthonormale,
![Rendered by QuickLaTeX.com \[\|e_i\|=\sqrt{\frac{n+1}{n}}\times\sqrt{\left(\frac{n}{n+1}\right)^2 + n\times\frac{1}{(n+1)^2}} =\sqrt{\frac{n+1}{n}}\times\sqrt{\frac{n(n+1)}{(n+1)^2}}=1\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e1ee3b973504b679750504909669b356_l3.png)
Conclusion : Pour tout ![]() , on a :
, on a : ![]() .
.
3/ b/ Soient ![]() un couple d’entiers distincts de
un couple d’entiers distincts de ![]() , on a :
, on a :
![]()
et par linéarité du produit scalaire :
![]()
Or, ![]() est orthonormale et nous avons vu dans 3.(a) que, pour tout
est orthonormale et nous avons vu dans 3.(a) que, pour tout ![]() ,
, ![]() , donc :
, donc :
![]()
Conclusion : Pour tout ![]() un couple d’entiers distincts de
un couple d’entiers distincts de ![]() , on a :
, on a : ![]()
3/ c/ Montrons que, pour tout ![]() ,
, ![]() , on aura alors le résultat démandé.
, on aura alors le résultat démandé.
Soit ![]() , on a :
, on a :
![]()
Conclusion : Pour tout ![]() ,
, ![]()
3/ d/ On a : ![]() (car
(car ![]() ). Il suffit alors de montrer que les
). Il suffit alors de montrer que les ![]() vecteurs
vecteurs ![]() de
de ![]() forment une famille libre. Considérons une combinaison linéaire égale à
forment une famille libre. Considérons une combinaison linéaire égale à ![]() :
:
![]()
On a alors, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\langle\sum\limits_{i=1}^{n}\alpha_i e_i,e_j\rangle=\sum\limits_{i=1}^{n}\alpha_i\langle e_i,e_j\rangle=0_E\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e432e8da9dea540c80dcae3de10a881c_l3.png)
Ou encore avec les conclusions de 3. (a) et (b) :
![Rendered by QuickLaTeX.com \[\sum\limits_{\substack{1\leqslant i\leqslant n\\i\neq j}}\frac{-\alpha_i}{n}+\alpha_j=\frac{-1}{n}\left( \sum\limits_{\substack{1\leqslant i\leqslant n\\i\neq j}}\alpha_i -n\alpha_j\right)=0_E\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-33608adda78fe348e297f5982a3522f9_l3.png)
Donc, pour tout
![Rendered by QuickLaTeX.com \[\sum\limits_{\substack{1\leqslant i\leqslant n\\i\neq j}}\alpha_i -n\alpha_j=0_E\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0074f271d33f883aad02ab13d3bd03cf_l3.png)
et
Conclusion : ![]() est une base de
est une base de ![]() .
.
4/ a/ Pour tout ![]() et tout
et tout ![]() , on a :
, on a :
![]() et
et ![]() ,
, ![]() est donc une forme symétrique.
est donc une forme symétrique.
![Rendered by QuickLaTeX.com \[f(\lambda x+y,z)=\sum\limits_{k=0}^{n} \langle \lambda x+y,e_k\rangle\langle z,e_k\rangle -\frac{n+1}{n}\langle \lambda x+y,z\rangle\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3fe4835460064c49018c72ed7a678f61_l3.png)
![Rendered by QuickLaTeX.com \[f(\lambda x+y,z)=\sum\limits_{k=0}^{n} \left(\lambda\langle x,e_k\rangle\langle z,e_k\rangle + \langle y,e_k\rangle\langle z,e_k\rangle\right) -\frac{n+1}{n}\left(\lambda\langle x,z\rangle+\langle y,z\rangle\right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b610d2583aa420612ad4a6392fe1d151_l3.png)
![Rendered by QuickLaTeX.com \[f(\lambda x+y,z)=\lambda\left(\sum\limits_{k=0}^{n} \langle x,e_k\rangle\langle z,e_k\rangle -\frac{n+1}{n}\langle x,z\rangle\right) + \sum\limits_{k=0}^{n} \langle y,e_k\rangle\langle z,e_k\rangle -\frac{n+1}{n}\langle y,z\rangle\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b0b5c585e44ec3d46df6c75051ef47a4_l3.png)
ou encore, ![]() , et
, et ![]() étant symétrique,
étant symétrique, ![]() est alors bien bilinéaire.
est alors bien bilinéaire.
Conclusion : ![]() est une forme bilinéaire et symétrique.
est une forme bilinéaire et symétrique.
4/ b/ Pour tout ![]() ,
,  .
.
Or, d’après les questions précédentes, pour ![]() ,
, ![]() et
et ![]() , donc :
, donc :
D’une part avec ![]() ,
,
![Rendered by QuickLaTeX.com \[f(e_i,e_i)=\langle e_i,e_i\rangle^2+\sum\limits_{\substack{0\leqslant k\leqslant n\\k\neq i}} \langle e_i,e_k\rangle^2- \frac{n+1}{n}\langle e_i,e_i\rangle\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-28e5682b89179920d4fe9063c7df595e_l3.png)
![]()
D’autre part avec ![]() ,
,
![Rendered by QuickLaTeX.com \[f(e_i,e_j)=\langle e_i,e_i\rangle\langle e_j,e_i\rangle+\langle e_i,e_j\rangle\langle e_j,e_j\rangle+\sum\limits_{\substack{0\leqslant k\leqslant n\\k\neq i,k\neq j}} \langle e_i,e_k\rangle^2- \frac{n+1}{n}\langle e_i,e_j\rangle\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5131239badc5ccc52434603c12b60537_l3.png)
![]()
Conclusion : Pour tout ![]() ,
, ![]() .
.
4/ c/ D’après 3.(d), ![]() est une base de
est une base de ![]() et pour tout
et pour tout ![]() ,
, ![]() , donc
, donc ![]() est nulle sur
est nulle sur ![]() . Donc :
. Donc :
![Rendered by QuickLaTeX.com \[\forall (x,y)\in F^2, f(x,y)=\sum\limits_{k=0}^{n}\langle x,e_k\rangle\langle y,e_k\rangle - \frac{n+1}{n}\langle x,y\rangle = 0\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-341981c8345eb0714746d162ae13899a_l3.png)
Conclusion : Pour tout ![]() ,
,  .
.
4/ d/ Soit ![]() . En appliquant la conclusion précédente avec
. En appliquant la conclusion précédente avec ![]() , on obtient :
, on obtient :
![Rendered by QuickLaTeX.com \[\frac{n+1}{n}\langle x,x\rangle=\sum\limits_{k=0}^{n}\langle x,e_k\rangle\langle x,e_k\rangle\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-66f680341ab76112e2cc7a40c4565fa9_l3.png)
Soit encore :
![Rendered by QuickLaTeX.com \[\frac{n+1}{n}\|x\|^2=\sum\limits_{k=0}^{n}\langle x,e_k\rangle^2\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0686d43cfac532332d718534e8305760_l3.png)
Conclusion : Pour tout ![]() ,
, 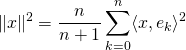 .
.
Problème 1 : Applications définies sur ![]()
Partie 1 : Étude d’une application définie sur ![Rendered by QuickLaTeX.com \mathbb{R}_n[ X ]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2046%2018%22%3E%3C/svg%3E)
1/ Pour tout ![]() et tout
et tout ![]() ,
, ![]() ,
, ![]() est donc bien une application de
est donc bien une application de ![]() dans
dans ![]() . De plus, pour tout
. De plus, pour tout ![]() et tout
et tout ![]() , on a:
, on a:
![Rendered by QuickLaTeX.com \[\varphi(\lambda P+Q)=\sum\limits_{k=0}^{n}(\lambda P+Q)^{(k)}=\sum\limits_{k=0}^{n}\left(\lambda P^{(k)}+Q^{(k)}\right)=\lambda \sum\limits_{k=0}^{n}P^{(k)}+\sum\limits_{k=0}^{n}Q^{(k)}=\lambda\varphi(P)+\varphi(Q)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-965168a9fec30c40fc9fffff31270d08_l3.png)
Conclusion : ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
2/ a/ ![]() est le polynôme constant égal à 1, donc pour tout
est le polynôme constant égal à 1, donc pour tout ![]() ,
, ![]() est nul. Donc :
est nul. Donc :
![Rendered by QuickLaTeX.com \[\varphi(e_0)=\sum\limits_{k=0}^{n}(e_0)^{(k)}=e_0\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e15daddf18acfe263d824949c29b9c1f_l3.png)
De plus, ![]() n’est pas le polynôme nul.
n’est pas le polynôme nul.
Conclusion : ![]() et
et ![]() est une valeur propore de
est une valeur propore de ![]() .
.
2/ b/ Soit ![]() . On a :
. On a :
![Rendered by QuickLaTeX.com \[\varphi(e_j)-e_j=e_j+\sum\limits_{k=1}^{n}(e_j)^{(k)}-e_j=\sum\limits_{k=1}^{n}(e_j)^{(k)}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0d66426a065ccaefd48457c27224f4fa_l3.png)
Or,
Conclusion : ![]() .
.
2/ c/ D’après les questions précédentes, ![]() et pour tout
et pour tout ![]() , il existe
, il existe ![]() tel que
tel que ![]() . La matrice de
. La matrice de ![]() dans la base
dans la base ![]() s’écrit donc :
s’écrit donc :
![Rendered by QuickLaTeX.com \[\mathrm{Mat}_{\mathscr{B}}(\varphi)=\begin{pmatrix}1 & \times & \cdots & \times\\0 & \ddots & \ddots & \vdots\\\vdots & \ddots & \ddots & \times\\0 & \dots & 0 & 1\end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8dd8e7a564580c23eed2063a63dfadf9_l3.png)
Cette matrice étant triangulaire, les valeurs propres de ![]() sont alors les coeffcients diagonaux.
sont alors les coeffcients diagonaux.
Conclusion : La matrice de ![]() dans la base
dans la base ![]() est donc triangulaire supérieure, l’unique valeur propre de
est donc triangulaire supérieure, l’unique valeur propre de ![]() est
est ![]() .
.
2/ d/ ![]() est triangulaire supérieure à coeffcients diagonaux non nul, elle est donc inversible et
est triangulaire supérieure à coeffcients diagonaux non nul, elle est donc inversible et ![]() est alors un endomorphisme bijectif.
est alors un endomorphisme bijectif.
Conclusion: ![]() est un automorphisme de
est un automorphisme de ![]() .
.
3/ a/ Soit ![]() . On a
. On a ![]() et par télescopage :
et par télescopage :
![Rendered by QuickLaTeX.com \[\varphi(P-P')=\sum\limits_{k=0}^{n}\left(P-P'\right)^{(k)}=\sum\limits_{k=0}^{n}\left(P^{(k)}-P^{(k+1)}\right)=P-P^{(n+1)}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-176540edf344b962bd6b2efbecd1ed93_l3.png)
Or, ![]() , donc
, donc ![]() est nul.
est nul.
Conclusion : Pour tout ![]() ,
, ![]() .
.
3/ b/ Posons ![]() définie pour tout
définie pour tout ![]() par
par ![]() .
. ![]() est un endomorphisme de
est un endomorphisme de ![]() et d’après la question précédente :
et d’après la question précédente :
![]()
On a alors ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
Conclusion : ![]() est définie pour tout
est définie pour tout ![]() par
par ![]() et la matrice de
et la matrice de ![]() dans la base
dans la base ![]() est :
est :
![Rendered by QuickLaTeX.com \[\mathrm{Mat}_{\mathscr{B}}(\varphi^{-1})=\begin{pmatrix}1 & -1 & 0 &\cdots & 0\\0 & 1 & -2 & \ddots & \vdots\\\vdots & \ddots & \ddots & \ddots & 0\\\vdots & & \ddots & \ddots & -k\\0 & \dots & \dots & 0 & 1\end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-87d3388eefa33fd6dd24bfe395cb221f_l3.png)
3/ c/ La deuxième ligne du programme crée ![]() , la matrice identité d’ordre
, la matrice identité d’ordre ![]() , puis la boucle change les coefficents au dessus de la diagonale pour que
, puis la boucle change les coefficents au dessus de la diagonale pour que ![]() soit égale à
soit égale à ![]() . Pour obtenir
. Pour obtenir ![]() il suffit alors d’inverser
il suffit alors d’inverser ![]() .
.
n=input(‘entrez la valeur de n : ‘)
M=eye(n+1,n+1)
for k=1:n
M(k,k+1)=-k
end
A=inv(M)
disp(A)
Partie 2 : Étude d’une autre application définie sur ![Rendered by QuickLaTeX.com \mathbb{R}_n[ X ]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2046%2018%22%3E%3C/svg%3E)
4/ a/ Soit ![]() . Par croissance comparée,
. Par croissance comparée, ![]() et donc
et donc ![]() . Or, pour tout
. Or, pour tout ![]() ,
, ![]() converge et donc, par le critère de négligeabilité des intégrales de fonctions positives au voisinage de
converge et donc, par le critère de négligeabilité des intégrales de fonctions positives au voisinage de ![]() ,
, ![]() converge.
converge.
Conclusion : Pour tout ![]() et tout
et tout ![]() ,
, ![]() converge.
converge.
4/ b/ Si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() .
.
Or, d’après (a), pour tout ![]() ,
, ![]() converge, donc
converge, donc ![]() converge comme combinaison linéaire d’intégrales convergentes.
converge comme combinaison linéaire d’intégrales convergentes.
Conclusion : Pour tout ![]() et tout
et tout ![]() ,
, ![]() converge.
converge.
5/ a/ Calculons cette intégrale. Pour tout ![]() , on a :
, on a :
![]()
Or, ![]() , donc l’intégrale converge et vaut
, donc l’intégrale converge et vaut ![]() .
.
Conclusion : Pour tout ![]() ,
, ![]() .
.
5/ b/ Par récurrence sur ![]() . Pour
. Pour ![]() c’est la question précédente.
c’est la question précédente.
Supposons que, pour un certain rang ![]() on ait :
on ait : 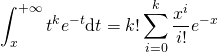 . Effectuons alors une intégration par parties pour calculer
. Effectuons alors une intégration par parties pour calculer ![]() .
.
![]() et
et ![]() sont bien de classe
sont bien de classe ![]() sur
sur ![]() ,
,![]() et
et ![]() , et pour tout
, et pour tout ![]() :
:
![]()
![]()
Or, par croissance comparée, ![]() et la convergence de l’intégrale étant déjà acquise, on en déduit :
et la convergence de l’intégrale étant déjà acquise, on en déduit :
![]()
Soit encore, d’après l’hypothèse de récurrence :
![Rendered by QuickLaTeX.com \[\int_x^{+\infty}t^{k+1}e^{-t}\mathrm{d}t=x^{k+1}e^{-x}+(k+1)k!\sum\limits_{i=0}^{k}\frac{x^i}{i!}e^{-x}=(k+1)!\sum\limits_{i=0}^{k+1}\frac{x^i}{i!}e^{-x}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ff46be04b24b40d6142e39c3cb01527c_l3.png)
L’hypothèse étant initialisée pour ![]() et héréditaire, elle est alors vraie pour tout
et héréditaire, elle est alors vraie pour tout ![]() .
.
Conclusion : Pour tout ![]() et tout
et tout ![]() ,
, 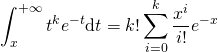 .
.
6/ a/ D’après l’énoncé, p=prod(1:k) est égal à ![]()
k=input(‘entrez la valeur de k : ‘)
x=input(‘entrez la valeur de x : ‘)
p=prod(1:k)
u=x.^(1:k)./cumprod(1:k)
s=p*(1+sum(u))*exp(-x)
disp(s)
u est le vecteur dont les coordonnées sont ![]()
6/ b/ ![]() étant fixé dans
étant fixé dans ![]() , posons
, posons ![]() qui est bien un changement de variable de classe
qui est bien un changement de variable de classe ![]() sur
sur ![]() . On a alors, pour
. On a alors, pour ![]() :
:
![]()
et la convergence quand ![]() étant déjà acquise, on a bien le résultat demandé.
étant déjà acquise, on a bien le résultat demandé.
Conclusion : Pour tout ![]() ,
, ![]() .
.
On sait, grâce au théorème de transfert et les intégrales étant convergentes, que : ![]() est l’espérance d’une variable
est l’espérance d’une variable ![]() où
où ![]() suit la loi exponentielle de paramètre
suit la loi exponentielle de paramètre ![]() . Pour obtenir une valeur approchée de cette intégrale avec la méthode de Monte-Carlo, il suffit de simuler un grand nombre (ici
. Pour obtenir une valeur approchée de cette intégrale avec la méthode de Monte-Carlo, il suffit de simuler un grand nombre (ici ![]() ) de réalisations indépendantes de variables
) de réalisations indépendantes de variables ![]() et donc :
et donc :
x=input(‘entrez la valeur de x : ‘)
k=input(‘entrez la valeur de k : ‘)
Z=grand(1,100000,’exp’,1)
s=exp(-x)*mean((Z+x).^k)
disp(s)
7/ a/ Soient ![]() et
et ![]() .
. ![]() et donc, d’après 4.(b), les intégrales suivantes sont, pour tout
et donc, d’après 4.(b), les intégrales suivantes sont, pour tout ![]() , toutes convergentes et :
, toutes convergentes et :
![]()
et donc, en multipliant par ![]() , on obtient :
, on obtient :
![]()
Autrement dit, ![]() et
et ![]() est linéaire.
est linéaire.
Montrons maintenant que, pour tout ![]() ,
, ![]() . Pour cela, il suffit de le vérifier pour les polynômes de la base canonique de
. Pour cela, il suffit de le vérifier pour les polynômes de la base canonique de ![]() , la linéarité fera le reste. Soit alors
, la linéarité fera le reste. Soit alors ![]() . D’après 5.(b) et la définition de
. D’après 5.(b) et la définition de ![]() , pour tout
, pour tout ![]() :
:
 = e^x\times\left(k!\sum\limits_{i=0}^{k}\frac{x^i}{i!}e^{-x}\right)=\sum\limits_{i=0}^{k}\frac{k!}{i!}x^i \in \mathbb{R}_n[X]\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b831a4d02d501597d1159fb091cd07cf_l3.png)
et donc, par linéarité de ![]() , pour tout
, pour tout ![]() .
.
Conclusion : ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
7/ b/ D’après la question précédente, ![]() est un polynôme et est donc bien de classe
est un polynôme et est donc bien de classe ![]() sur
sur ![]() . De plus, la convergence permet d’écrire la relation de Chasles, valable pour tout
. De plus, la convergence permet d’écrire la relation de Chasles, valable pour tout ![]() :
:
![]()
![]() est alors une constante, donc de dérivée nulle par rapport à
est alors une constante, donc de dérivée nulle par rapport à ![]() et d’après le théorème fondamental du calcul,
et d’après le théorème fondamental du calcul, ![]() est dérivable de dérivée :
est dérivable de dérivée : ![]() .
.
En dérivant, par rapport à ![]() la fonction produit
la fonction produit ![]() , on a :
, on a :
![]()
Conclusion : ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]() .
.
7/ c/ Notons ![]() le polynôme nul et soit
le polynôme nul et soit ![]() . On a alors
. On a alors ![]() . Donc
. Donc ![]() et d’après la question précédente :
et d’après la question précédente : ![]() , mais comme
, mais comme ![]() on a immédiatement
on a immédiatement ![]() . On en déduit que
. On en déduit que ![]() et l’inclusion réciproque étant evidente,
et l’inclusion réciproque étant evidente, ![]() et
et ![]() est injective. De plus
est injective. De plus ![]() est de dimension finie, l’endomorphisme
est de dimension finie, l’endomorphisme ![]() est alors, par corollaire du théorème du rang, bijectif.
est alors, par corollaire du théorème du rang, bijectif.
Conclusion : ![]() est un automorphisme de
est un automorphisme de ![]() .
.
8/ a/ Avec les donnée de l’énoncé, on a ![]() et, d’après 7.(b),
et, d’après 7.(b), ![]() . Donc :
. Donc : ![]() . Reste alors à diviser par
. Reste alors à diviser par ![]() .
.
Conclusion : Pour ![]() vecteur propre associé à une valeur propre
vecteur propre associé à une valeur propre ![]() , on a :
, on a : ![]() .
.
8/ b/ Remarquons tout d’abord que ![]() ne peut pas être valeur propre puisque
ne peut pas être valeur propre puisque ![]() est un automorphisme.
est un automorphisme.
Posons ![]() . Si
. Si ![]() est constant (
est constant (![]() ) alors
) alors ![]() et comme
et comme ![]() , on a
, on a ![]() . Si
. Si ![]() n’est pas constant (
n’est pas constant (![]() ) alors
) alors ![]() ce qui est impossible car
ce qui est impossible car ![]()
Conclusion : ![]() est la seule valeur propre possible de
est la seule valeur propre possible de ![]() .
.
8/ c/ D’après 5.(a), pour tout ![]() ,
, ![]() . Donc,
. Donc, ![]() . Autrement dit,
. Autrement dit, ![]() et le polynôme constant égal à
et le polynôme constant égal à ![]() est un vecteur propre de
est un vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() . Avec la question précédente, on sait que c’est la seule.
. Avec la question précédente, on sait que c’est la seule.
Conclusion : ![]() est la seule valeur propre de
est la seule valeur propre de ![]() .
.
9/ a/ ![]() et
et ![]() sont tous les deux des automorphismes de
sont tous les deux des automorphismes de ![]() . Pour montrer que
. Pour montrer que ![]() et
et ![]() sont égaux il suffit de montrer qu’ils coïncident sur la base canonique. Soit
sont égaux il suffit de montrer qu’ils coïncident sur la base canonique. Soit ![]() , on a :
, on a :
D’une part
![]()
et donc :
![Rendered by QuickLaTeX.com \[\varphi(X^k)=\sum\limits_{i=0}^{n}(X^k)^{(i)}=\sum\limits_{i=0}^{k}\frac{k!}{(k-i)!}X^{k-i}=\sum\limits_{j=0}^{k}\frac{k!}{j!}X^{j}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-22711e420df1dff79c817f0e57d2ed17_l3.png)
La dernière éaglité étant obtenue par le renversement d’indice ![]() .
.
D’autre part, d’après 5.(b),
![Rendered by QuickLaTeX.com \[\Psi(X^k)=e^{x}\int_x^{+\infty}t^ke^{-t}\mathrm{d}t = e^x\left(k!\sum\limits_{i=0}^{k}\frac{x^i}{i!}e^{-x}\right)=\sum\limits_{i=0}^{k}\frac{k!}{i!}x^{i}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-472150480e1d3ed8b059ddbe90dbf4a3_l3.png)
Donc :
Conclusion : Les endomorphismes ![]() et
et ![]() sont égaux.
sont égaux.
9/ b/ Soient ![]() et
et ![]() tels que, pour tout
tels que, pour tout ![]() . Dans ce cas,
. Dans ce cas, ![]() est positive sur
est positive sur ![]() et par positivité de l’intégrale, on a :
et par positivité de l’intégrale, on a :
![]()
Mais comme ![]() et
et ![]() sont égaux, on a alors :
sont égaux, on a alors :
![]()
ce qui est exactement le résultat recherché.
Conclusion : ![]()

