Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EDHEC Maths ECS 2018
Revenir à tous les corrigés des annales maths BCE
Exercice 1 : Comparaison série-intégrale et étude de fonction
1/ Étudions la parité de ![]() . Pour tout
. Pour tout ![]() , on voit que :
, on voit que :
![]()
Par conséquent, on en déduit que :
![]()
2/ Montrons que ![]() peut être considérée comme une densité d’une certaine variable aléatoire
peut être considérée comme une densité d’une certaine variable aléatoire ![]() . Pour ce faire, il suffit de vérifier que
. Pour ce faire, il suffit de vérifier que ![]() est positive et continue sur
est positive et continue sur ![]() et que
et que ![]() converge et vaut
converge et vaut ![]() :
:
![]() Première étape :
Première étape : ![]() est positive et continue sur
est positive et continue sur ![]() .
.
Comme l’exponentielle est strictement positive sur ![]() , on voit que
, on voit que ![]() pour tout
pour tout ![]() . En particulier, la fonction
. En particulier, la fonction ![]() est positive et continue sur
est positive et continue sur ![]() comme inverse d’une fonction positive et continue sur
comme inverse d’une fonction positive et continue sur ![]() , dont le dénominateur ne s’annule pas sur
, dont le dénominateur ne s’annule pas sur ![]() .
.
Par conséquent :
![]()
![]() Deuxième étape : l’intégrale
Deuxième étape : l’intégrale ![]() converge et vaut
converge et vaut ![]() .
.
Fixons deux réels ![]() tels que
tels que ![]() . Alors on trouve par des calculs simples que :
. Alors on trouve par des calculs simples que :
![]()
Comme ![]() tend vers
tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() et que
et que ![]() tend vers
tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() , ceci entraine que :
, ceci entraine que :
![]()
Dès lors, il s’ensuit que :
![Rendered by QuickLaTeX.com \[ \boxed{\text{l'int\'egrale } \int_{-\infty} ^{+\infty} f(t)dt \text{ converge et vaut }1.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cd2f31bbdf6e2656bcc4262e718b21b6_l3.png)
Par conséquent, on en déduit que :
![]()
3/ a/ Montrons que ![]() possède une espérance et donnons sa valeur. Par définition, la variable aléatoire
possède une espérance et donnons sa valeur. Par définition, la variable aléatoire ![]() admet une espérance si et seulement si l’intégrale
admet une espérance si et seulement si l’intégrale ![]() converge absolument, c’est-à-dire converge. Comme la fonction
converge absolument, c’est-à-dire converge. Comme la fonction ![]() est paire d’après la question
est paire d’après la question ![]() , la fonction
, la fonction ![]() est impaire et il suffit de vérifier que l’intégrale
est impaire et il suffit de vérifier que l’intégrale ![]() converge. De plus, comme la fonction
converge. De plus, comme la fonction ![]() est continue sur
est continue sur ![]() comme produit de fonctions continues sur
comme produit de fonctions continues sur ![]() , l’intégrale
, l’intégrale ![]() présente juste une impropreté en
présente juste une impropreté en ![]() . Par des calculs simples, on trouve que, pour tout
. Par des calculs simples, on trouve que, pour tout ![]() :
:
![]()
Comme l’expression de droite ci-dessus tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() par croissances comparées, le théorème d’encadrement entraine que
par croissances comparées, le théorème d’encadrement entraine que ![]() tend vers
tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() , et donc :
, et donc :
![]()
Comme l’intégrale de Riemann ![]() converge d’après le cours et qu’il s’agit de l’intégrale d’une fonction positive, l’intégrale
converge d’après le cours et qu’il s’agit de l’intégrale d’une fonction positive, l’intégrale ![]() converge d’après le critère de négligeabilité. D’après la relation de Chasles, l’intégrale
converge d’après le critère de négligeabilité. D’après la relation de Chasles, l’intégrale ![]() converge, et donc :
converge, et donc :
![]()
Comme de plus la fonction ![]() est impaire, on en déduit que
est impaire, on en déduit que ![]() , et donc :
, et donc :
![]()
3/ b/ Montrons que ![]() possède une variance. Par définition, la variable aléatoire
possède une variance. Par définition, la variable aléatoire ![]() admet une variance si et seulement si l’intégrale
admet une variance si et seulement si l’intégrale ![]() converge absolument, c’est-à-dire converge. Comme la fonction
converge absolument, c’est-à-dire converge. Comme la fonction ![]() est paire d’après la question
est paire d’après la question ![]() , la fonction
, la fonction ![]() est paire et il suffit de vérifier que l’intégrale
est paire et il suffit de vérifier que l’intégrale ![]() converge. De plus, comme la fonction
converge. De plus, comme la fonction ![]() est continue sur
est continue sur ![]() comme produit de fonctions continues sur
comme produit de fonctions continues sur ![]() , l’intégrale
, l’intégrale ![]() présente juste une impropreté en
présente juste une impropreté en ![]() . Par des calculs simples, on trouve que, pour tout
. Par des calculs simples, on trouve que, pour tout ![]() :
:
![]()
Comme l’expression de droite ci-dessus tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() par croissances comparées, le théorème d’encadrement entraine que
par croissances comparées, le théorème d’encadrement entraine que ![]() tend vers
tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() , et donc :
, et donc :
![]()
Comme l’intégrale de Riemann ![]() converge d’après le cours et qu’il s’agit de l’intégrale d’une fonction positive, l’intégrale
converge d’après le cours et qu’il s’agit de l’intégrale d’une fonction positive, l’intégrale ![]() converge d’après le critère de négligeabilité. D’après la relation de Chasles, l’intégrale
converge d’après le critère de négligeabilité. D’après la relation de Chasles, l’intégrale ![]() converge, et donc :
converge, et donc :
![]()
4/ On note ![]() la fonction de répartition de
la fonction de répartition de ![]() . Montrons que
. Montrons que ![]() est une bijection de
est une bijection de ![]() sur
sur ![]() . Comme
. Comme ![]() est la fonction de répartition d’une variable à densité, elle est continue sur
est la fonction de répartition d’une variable à densité, elle est continue sur ![]() . De plus, comme la fonction
. De plus, comme la fonction ![]() est continue et strictement positive sur
est continue et strictement positive sur ![]() , la fonction
, la fonction ![]() est dérivable sur
est dérivable sur ![]() et de plus, on a pour tout
et de plus, on a pour tout ![]() :
:
![]()
En particulier, la fonction ![]() est continue et strictement croissante sur
est continue et strictement croissante sur ![]() . D’après le théorème de la bijection, la fonction
. D’après le théorème de la bijection, la fonction ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() . Comme
. Comme ![]() est continue sur l’intervalle
est continue sur l’intervalle ![]() , son image
, son image ![]() est un intervalle d’après le théorème des valeurs intermédiaires. Comme
est un intervalle d’après le théorème des valeurs intermédiaires. Comme ![]() est strictement croissante sur
est strictement croissante sur ![]() , qu’elle tend vers
, qu’elle tend vers ![]() en
en ![]() et vers
et vers ![]() en
en ![]() (en tant que fonction de répartition), il s’ensuit que
(en tant que fonction de répartition), il s’ensuit que ![]() . Par conséquent, on en déduit que :
. Par conséquent, on en déduit que :
![]()
5/ On considère la variable aléatoire ![]() définie par
définie par ![]() .
.
a/ Déterminons la loi de ![]() . Pour ce faire, on note
. Pour ce faire, on note ![]() sa fonction de répartition. Comme
sa fonction de répartition. Comme ![]() est à valeurs dans
est à valeurs dans ![]() , la variable aléatoire
, la variable aléatoire ![]() est à support dans
est à support dans ![]() , et donc
, et donc ![]() si
si ![]() et
et ![]() si
si ![]() . De plus, comme
. De plus, comme ![]() est la fonction de répartition de
est la fonction de répartition de ![]() et que c’est une bijection strictement croissante de
et que c’est une bijection strictement croissante de ![]() sur
sur ![]() , on voit que, pour tout
, on voit que, pour tout ![]() :
:
![]()
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{G(x)=\left \{\begin{array}{lll}0 & \text{si} & x\leq 0 \\x & \text{si} & x\in ]0,1[ \\1 & \text{si} & x\geq 1\end{array}\right. .}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-94a4ce0682301c1b20eaa35bc4664f2c_l3.png)
Au vu de cette fonction de répartition, on en déduit aussi que :
![]()
b/ Déterminons explicitement ![]() pour tout réel
pour tout réel ![]() . Par des calculs simples, on a pour tout
. Par des calculs simples, on a pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{array}{lll}F(x) & =& \displaystyle \int_{-\infty} ^x f(t)dt \\& & \\& = & \displaystyle \lim_{y\to -\infty} \int_y ^x f(t)dt \\& & \\& = & \displaystyle \lim_{y\to -\infty} \int_y ^x \frac{2}{\left(e^t + e^{-t}\right)^2}dt \\& & \\& = & \displaystyle \lim_{y\to -\infty} \int_y ^x \frac{2e^{2t} }{\left(e^{2t} + 1\right)^2}dt \\& & \\& = & \displaystyle \lim_{y\to -\infty} \left [ - \frac{1}{\left(e^{2t} + 1\right)}\right ]_y ^x \\& & \\& = & \displaystyle \lim_{y\to -\infty} - \frac{1}{\left(e^{2x} + 1\right)}+\frac{1}{\left(e^{2y} + 1\right)} \\& & \\& = & \displaystyle 1-\frac{1}{e^{2x} + 1}.\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3e11e5f823c3c3490d1c6709a9b5f1df_l3.png)
Par conséquent, on en déduit que, pour tout ![]() :
:
![]()
c/ Établissons que la fonction ![]() , bijection réciproque de
, bijection réciproque de ![]() , est définie par :
, est définie par :
![]()
Fixons un réel ![]() . Par définition, le réel
. Par définition, le réel ![]() est l’unique antécédent de
est l’unique antécédent de ![]() par
par ![]() , c’est-à-dire l’unique réel
, c’est-à-dire l’unique réel ![]() tel que
tel que ![]() . D’après la question précédente, on trouve que :
. D’après la question précédente, on trouve que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}x=F(y) &\Longleftrightarrow & \displaystyle x=1-\frac{1}{e^{2y} + 1} \\& & \\& \Longleftrightarrow & \displaystyle \frac{1}{e^{2y}+1}=1-x \\& & \\& \Longleftrightarrow & \displaystyle e^{2y}+1=\frac{1}{1-x} \\& & \\& \Longleftrightarrow & \displaystyle e^{2y}=\frac{1}{1-x}-1=\frac{x}{1-x} \\& & \\& \Longleftrightarrow & \displaystyle 2y=\ln \left (\frac{x}{1-x}\right )\\& & \\& \Longleftrightarrow & \displaystyle y=\frac12 \ln \left (\frac{x}{1-x}\right ).\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2d3f65a8b32fcc2b6ea67b29f67f0e86_l3.png)
Par conséquent, on en déduit que la bijection réciproque de ![]() est donnée pour tout
est donnée pour tout ![]() par :
par :
![Rendered by QuickLaTeX.com \[ \boxed{F^{-1}(x)=\frac12 \ln \left (\frac{x}{1-x}\right ).}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a26e7cc302969d7daa49c01d1adda61b_l3.png)
d/ Écrivons un script Scilab permettant de simuler la variable aléatoire ![]() . Pour ce faire, on part du principe que, d’après les questions précédentes, la variable aléatoire
. Pour ce faire, on part du principe que, d’après les questions précédentes, la variable aléatoire ![]() suit la loi uniforme sur
suit la loi uniforme sur ![]() (laquelle peut se simuler à l’aide de la commande « rand ») et que
(laquelle peut se simuler à l’aide de la commande « rand ») et que ![]() . Dès lors, pour simuler la variable aléatoire
. Dès lors, pour simuler la variable aléatoire ![]() , on pourra utiliser l’instruction suivante :
, on pourra utiliser l’instruction suivante :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{l}Y=\text{rand}\; ; \\X=0.5*\text{log}(Y/(1-Y)) \\\end{array}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b6bcc49d18b9c48490c89db27377aece_l3.png)
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : norme, variables aléatoires, loi de Bernouilli
Partie 1 :
1/ Calculons ![]() en fonction de
en fonction de ![]() . Pour ce faire, on pose
. Pour ce faire, on pose ![]() . Par des calculs simples, on trouve que :
. Par des calculs simples, on trouve que :
![Rendered by QuickLaTeX.com \[\qquad \qquad\begin{array}{lll}M & = & \displaystyle A^2-(a+d)A \\& & \\& = & \displaystyle \begin{pmatrix}a & c \\b & d\end{pmatrix}\begin{pmatrix}a & c \\b & d\end{pmatrix} -(a+d) \begin{pmatrix}a & c \\b & d\end{pmatrix} \\& & \\& = & \displaystyle \begin{pmatrix}a^2+bc & ac+cd \\ab+bd & bc+d^2\end{pmatrix} -\begin{pmatrix}a^2+ad & ac+cd \\ab+bd & ad+d^2\end{pmatrix} \\& & \\& = & \displaystyle \begin{pmatrix}bc -ad& 0\\0& bc-ad\end{pmatrix} \quad = \quad (bc-ad)\begin{pmatrix}1& 0\\0& 1\end{pmatrix}.\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3d74bc89eace682e5940415a0b672e9f_l3.png)
Par conséquent, on en déduit que :
![]()
2/ On suppose dans cette question que ![]() est nilpotente d’indice
est nilpotente d’indice ![]() .
.
a/ Établissons l’égalité : ![]() . En multipliant l’égalité de la question précédente par
. En multipliant l’égalité de la question précédente par ![]() , on obtient que :
, on obtient que :
![]()
Comme ![]() par définition de l’indice de nilpotence, on voit que
par définition de l’indice de nilpotence, on voit que ![]() , ce qui entraine que
, ce qui entraine que ![]() , et donc :
, et donc :
![]()
Mais comme ![]() , on en déduit que le réel
, on en déduit que le réel ![]() est nul, et donc :
est nul, et donc :
![]()
b/ Montrons que ![]() est supérieur ou égal à
est supérieur ou égal à ![]() . Pour ce faire, on raisonne par l’absurde et on suppose que
. Pour ce faire, on raisonne par l’absurde et on suppose que ![]() . Alors on voit que
. Alors on voit que ![]() , ce qui entraine que la matrice
, ce qui entraine que la matrice ![]() est nulle, d’où contradiction avec les hypothèses de la partie
est nulle, d’où contradiction avec les hypothèses de la partie ![]() . Par conséquent, on en déduit que :
. Par conséquent, on en déduit que :
![]()
c/ Montrons que ![]() . Comme
. Comme ![]() d’après la question précédente, on obtient en multipliant l’égalité de la question
d’après la question précédente, on obtient en multipliant l’égalité de la question ![]() par
par ![]() que :
que :
![]()
Comme ![]() par définition de l’indice de nilpotence et que
par définition de l’indice de nilpotence et que ![]() d’après la question
d’après la question ![]() , on trouve que :
, on trouve que :
![]()
Mais comme ![]() , on en déduit que le réel
, on en déduit que le réel ![]() est nul, et donc :
est nul, et donc :
![]()
3/ Montrons que : ![]() nilpotente
nilpotente ![]() . Pour ce faire, supposons que
. Pour ce faire, supposons que ![]() soit nilpotente. Alors on sait d’après les questions
soit nilpotente. Alors on sait d’après les questions ![]() et
et ![]() que
que ![]() et
et ![]() . D’après la relation de la question
. D’après la relation de la question ![]() , on obtient que :
, on obtient que :
![]()
et donc ![]() . Réciproquement, si
. Réciproquement, si ![]() , alors la matrice
, alors la matrice ![]() est manifestement nilpotente d’indice
est manifestement nilpotente d’indice ![]() .
.
Par conséquent, on en déduit que :
![]()
Partie 2 :
1/ a/ Montrons que, si ![]() , alors on a :
, alors on a : ![]() . Pour ce faire, considérons un élément
. Pour ce faire, considérons un élément ![]() de
de ![]() . Alors
. Alors ![]() appartient à
appartient à ![]() par définition. Comme
par définition. Comme ![]() , il s’ensuit que
, il s’ensuit que ![]() appartient à
appartient à ![]() , et donc
, et donc ![]() . Mais comme ceci est vrai pour tout
. Mais comme ceci est vrai pour tout ![]() , on en déduit que
, on en déduit que ![]() . Par conséquent :
. Par conséquent :
![]()
b/ On suppose que ![]() . Montrons tout d’abord que
. Montrons tout d’abord que ![]() . Pour ce faire, considérons un élément
. Pour ce faire, considérons un élément ![]() de
de ![]() . Alors il existe un vecteur
. Alors il existe un vecteur ![]() tel que
tel que ![]() . Comme
. Comme ![]() , on a :
, on a :
![]()
et donc ![]() appartient à
appartient à ![]() . Mais comme ceci est vrai pour tout
. Mais comme ceci est vrai pour tout ![]() , on en déduit que :
, on en déduit que :
![]()
A présent, établissons que ![]() , puis que
, puis que ![]() . Comme
. Comme ![]() , on obtient en passant aux dimensions que :
, on obtient en passant aux dimensions que :
![]()
Comme ![]() d’après le théorème du rang, ceci entraine avec l’inégalité ci-dessus que
d’après le théorème du rang, ceci entraine avec l’inégalité ci-dessus que ![]() , et donc
, et donc ![]() . Mais comme
. Mais comme ![]() est un endomorphisme non nul de
est un endomorphisme non nul de ![]() par hypothèse, on voit que
par hypothèse, on voit que ![]() , et donc :
, et donc :
![]()
De plus, comme ![]() d’après le théorème du rang, il s’ensuit que
d’après le théorème du rang, il s’ensuit que ![]() . Mais comme
. Mais comme ![]() d’après ce qui précède, on en déduit par égalité des dimensions que :
d’après ce qui précède, on en déduit par égalité des dimensions que :
![]()
c/ Montrons, à l’aide de la partie 1, l’équivalence : ![]() . Pour ce faire, supposons que
. Pour ce faire, supposons que ![]() . Alors on sait d’après la question
. Alors on sait d’après la question ![]() que
que ![]() , et donc
, et donc ![]() est nilpotent. Réciproquement, supposons que
est nilpotent. Réciproquement, supposons que ![]() soit nilpotent (d’indice
soit nilpotent (d’indice ![]() ). Fixons une base
). Fixons une base ![]() de
de ![]() et soit
et soit ![]() la matrice de
la matrice de ![]() dans cette base. Comme
dans cette base. Comme ![]() , on voit que
, on voit que ![]() , et donc
, et donc ![]() est nilpotente. De plus, comme
est nilpotente. De plus, comme ![]() est non nul, la matrice
est non nul, la matrice ![]() est non nulle. D’après la question
est non nulle. D’après la question ![]() de la partie
de la partie ![]() , on voit que
, on voit que ![]() , ce qui entraine que
, ce qui entraine que ![]() , et donc
, et donc ![]() d’après la question précédente. Par conséquent, on en déduit que :
d’après la question précédente. Par conséquent, on en déduit que :
![]()
On suppose dans toute la suite que ![]() est nilpotent et on en étudie quelques propriétés.
est nilpotent et on en étudie quelques propriétés.
2/ Montrons qu’il existe une base de ![]() dans laquelle la matrice
dans laquelle la matrice ![]() de
de ![]() est :
est :
![]()
Comme ![]() est nilpotent, on voit d’après les questions
est nilpotent, on voit d’après les questions ![]() ,
, ![]() et
et ![]() d’abord que
d’abord que ![]() , puis que
, puis que ![]() et enfin que
et enfin que ![]() .
.
Fixons un vecteur ![]() tel que
tel que ![]() (il en existe un car
(il en existe un car ![]() ) et posons
) et posons ![]() . Montrons tout d’abord que
. Montrons tout d’abord que ![]() est libre.
est libre.
Pour ce faire, on raisonne par l’absurde et on suppose que ![]() est liée. Comme
est liée. Comme ![]() , les vecteurs
, les vecteurs ![]() et
et ![]() sont non nuls et il existe un réel
sont non nuls et il existe un réel ![]() tel que
tel que ![]() . Comme
. Comme ![]() , on voit que
, on voit que ![]() par linéarité de
par linéarité de ![]() , ce qui entraine que
, ce qui entraine que ![]() , et donc
, et donc ![]() , d’où une contradiction.
, d’où une contradiction.
Dès lors, comme la famille ![]() est libre et que
est libre et que ![]() , la famille
, la famille ![]() est une base de
est une base de ![]() . Comme
. Comme ![]() et que
et que ![]() , il s’ensuit que :
, il s’ensuit que :
![]()
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{\text{il existe une base de } E \text{ dans laquelle la matrice } A \text{ de } f \text{ est : }A = \begin{pmatrix} 0 &1 \\ 0 & 0\end{pmatrix}.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d1a93623b8b7d67b0d54627b13d60d2c_l3.png)
3/ On souhaite montrer par l’absurde qu’il est impossible de trouver deux endomorphismes ![]() et
et ![]() de
de ![]() , nilpotents et tels que
, nilpotents et tels que ![]() . On suppose donc que ces deux endomorphismes existent.
. On suppose donc que ces deux endomorphismes existent.
a/ Montrons les inclusions : ![]() et
et ![]() . Pour ce faire, considérons un élément
. Pour ce faire, considérons un élément ![]() de
de ![]() . Alors il existe un vecteur
. Alors il existe un vecteur ![]() tel que
tel que ![]() . Comme
. Comme ![]() , on voit que
, on voit que ![]() , ce qui entraine que
, ce qui entraine que ![]() appartient à
appartient à ![]() . Mais comme ceci est vrai pour tout
. Mais comme ceci est vrai pour tout ![]() , on en déduit que :
, on en déduit que :
![]()
A présent, considérons un élément ![]() de
de ![]() . Alors on voit que
. Alors on voit que ![]() . Comme
. Comme ![]() , ceci entraine que
, ceci entraine que ![]() car
car ![]() est linéaire, et donc
est linéaire, et donc ![]() appartient à
appartient à ![]() . Mais comme ceci est vrai pour tout
. Mais comme ceci est vrai pour tout ![]() , on en déduit que :
, on en déduit que :
![]()
b/ Etablissons les égalités : ![]() et
et ![]() . Comme
. Comme ![]() est un endomorphisme non nul et que
est un endomorphisme non nul et que ![]() , on voit que
, on voit que ![]() et
et ![]() sont non nuls. Dès lors, comme
sont non nuls. Dès lors, comme ![]() sont des endomorphismes non nuls et nilpotents de
sont des endomorphismes non nuls et nilpotents de ![]() , on obtient d’après la question
, on obtient d’après la question ![]() de la partie
de la partie ![]() que
que ![]() . Mais comme
. Mais comme ![]() et que
et que ![]() d’après la question précédente, il s’ensuit par égalité des dimensions que :
d’après la question précédente, il s’ensuit par égalité des dimensions que :
![]()
De même, comme ![]() , on obtient avec le théorème du rang que :
, on obtient avec le théorème du rang que :
![]()
Mais comme ![]() d’après la question précédente, il s’ensuit que :
d’après la question précédente, il s’ensuit que :
![]()
c/ Montrons l’égalité : ![]() . Comme
. Comme ![]() est un endomorphisme non nul et que
est un endomorphisme non nul et que ![]() , on voit que
, on voit que ![]() et
et ![]() sont non nuls. Dès lors, comme
sont non nuls. Dès lors, comme ![]() sont des endomorphismes non nuls et nilpotents de
sont des endomorphismes non nuls et nilpotents de ![]() , on obtient d’après la question
, on obtient d’après la question ![]() de la partie
de la partie ![]() que
que ![]() ,
, ![]() et
et ![]() . Mais comme
. Mais comme ![]() et
et ![]() d’après la question précédente, il s’ensuit que :
d’après la question précédente, il s’ensuit que :
![]()
Par conséquent, on en déduit que :
![]()
d/ Montrons qu’il est impossible de trouver deux endomorphismes ![]() et
et ![]() de
de ![]() , nilpotents et tels que
, nilpotents et tels que ![]() . Pour ce faire, on raisonne par l’absurde et on suppose que de tels endomorphismes
. Pour ce faire, on raisonne par l’absurde et on suppose que de tels endomorphismes ![]() existent. D’après la question précédente, on sait que
existent. D’après la question précédente, on sait que ![]() . Dès lors, pour tout
. Dès lors, pour tout ![]() , le vecteur
, le vecteur ![]() appartient à
appartient à ![]() , et donc :
, et donc :
![]()
Comme ceci est vrai pour tout ![]() , il s’ensuit que
, il s’ensuit que ![]() est l’endomorphisme nul, ce qui contredit l’hypothèse de départ. Par conséquent, on en déduit que :
est l’endomorphisme nul, ce qui contredit l’hypothèse de départ. Par conséquent, on en déduit que :
![]()
Exercice 3 : Somme Harmonique
1/ a/ Déterminons tout d’abord le rang de ![]() . Comme la matrice
. Comme la matrice ![]() a tous ses coefficients non nuls, on voit que
a tous ses coefficients non nuls, on voit que ![]() . De plus, comme tous ses coefficients sont égaux à
. De plus, comme tous ses coefficients sont égaux à ![]() , toutes les colonnes de
, toutes les colonnes de ![]() sont proportionnelles entre elles, et donc
sont proportionnelles entre elles, et donc ![]() . Par conséquent, on en déduit que :
. Par conséquent, on en déduit que :
![]()
Comme ![]() , on en déduit aussi que :
, on en déduit aussi que :
![]()
Enfin, déterminons la dimension du sous-espace propre associé. Pour ce faire, on désigne par ![]() l’endomorphisme de
l’endomorphisme de ![]() canoniquement associé à
canoniquement associé à ![]() . Comme
. Comme ![]() est valeur propre de
est valeur propre de ![]() ,
, ![]() est aussi valeur propre de
est aussi valeur propre de ![]() et de plus
et de plus ![]() . D’après le théorème du rang, on trouve que :
. D’après le théorème du rang, on trouve que :
![]()
Par conséquent, on en déduit que :
![]()
b/ Vérifions que le vecteur ![]() élément de
élément de ![]() , dont toutes les composantes sont égales à
, dont toutes les composantes sont égales à ![]() , est vecteur propre de
, est vecteur propre de ![]() . Par des calculs simples, on trouve que :
. Par des calculs simples, on trouve que :
![Rendered by QuickLaTeX.com \[J_n V_n=\begin{pmatrix}1 & ... & 1 \\\vdots & & \vdots \\1 & ... & 1 \\\end{pmatrix}\begin{pmatrix}1 \\\vdots \\1 \\\end{pmatrix}= \begin{pmatrix}n \\\vdots \\n \\\end{pmatrix}=n\begin{pmatrix}1 \\\vdots \\1 \\\end{pmatrix}=nV_n.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-242c8e556ed6465fe52421624042f222_l3.png)
Comme ![]() , on en déduit que :
, on en déduit que :
![]()
c/ Donnons les valeurs propres de ![]() . Comme
. Comme ![]() est vecteur propre de
est vecteur propre de ![]() pour la valeur propre
pour la valeur propre ![]() , on voit que
, on voit que ![]() . Comme de plus
. Comme de plus ![]() d’après la question
d’après la question ![]() , on obtient que :
, on obtient que :
![]()
Mais comme la somme des dimensions des sous-espaces propres est ![]() pour toute matrice carrée de taille
pour toute matrice carrée de taille ![]() , ceci entraine que :
, ceci entraine que :
![]()
En particulier, la matrice ![]() est diagonalisable et n’admet pas d’autre valeur propre que
est diagonalisable et n’admet pas d’autre valeur propre que ![]() et
et ![]() . Par conséquent, on en déduit que :
. Par conséquent, on en déduit que :
![]()
Dans toute la suite, on considère la fonction ![]() définie sur
définie sur ![]() par :
par :
![Rendered by QuickLaTeX.com \[\forall x = (x_1,x_2,\dots,x_n) \in \mathbb{R}^n,\quad f_n(x) = \left(\sum_{k=1}^n x_k\right) \exp\left(-\sum_{k=1}^n x_k^2\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0d24aeb3396b9f92ec3dc9bf2180070d_l3.png)
1/ Montrons que ![]() est de classe
est de classe ![]() sur
sur ![]() . Comme les fonctions
. Comme les fonctions ![]() et
et ![]() sont polynomiales sur
sont polynomiales sur ![]() , elles sont de classe
, elles sont de classe ![]() sur
sur ![]() . Mais comme la fonction exponentielle est de classe
. Mais comme la fonction exponentielle est de classe ![]() sur
sur ![]() , il s’ensuit par composition et produit que :
, il s’ensuit par composition et produit que :
![]()
2/ a/ Montrons que, pour tout ![]() , on a :
, on a :
![Rendered by QuickLaTeX.com \[\partial_i(f_n)(x) = \left(1-2x_i \displaystyle\sum_{k=1}^n x_k\right)\exp\left(-\displaystyle\sum_{k=1}^n x_k^2\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3f35c100678d692f733e93794025ed5d_l3.png)
Par des calculs simples, on trouve que, pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\partial_i(f_n)(x) &= & \displaystyle \partial_i \left(\sum_{k=1}^n x_k\right) \exp\left(-\sum_{k=1}^n x_k^2\right) +\left(\sum_{k=1}^n x_k\right)\partial_i \left (\exp\left(-\sum_{k=1}^n x_k^2\right)\right ) \\& & \\& = & \displaystyle 1.\exp\left(-\sum_{k=1}^n x_k^2\right) +\left(\sum_{k=1}^n x_k\right) \exp\left(-\sum_{k=1}^n x_k^2\right) \partial_i \left(-\sum_{k=1}^n x_k^2\right) \\& & \\& = & \displaystyle 1.\exp\left(-\sum_{k=1}^n x_k^2\right) +\left(\sum_{k=1}^n x_k\right) \exp\left(-\sum_{k=1}^n x_k^2\right) \left(-2x_i\right) \\& & \\& = & \displaystyle \left [1-2x_i\sum_{k=1}^n x_k\right ]\exp\left(-\sum_{k=1}^n x_k^2\right). \\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7494267c2a012b055f2d7fa139f0aed5_l3.png)
Par conséquent, on en déduit que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\partial_i(f_n)(x) = \left(1-2x_i \displaystyle\sum_{k=1}^n x_k\right)\exp\left(-\displaystyle\sum_{k=1}^n x_k^2\right).}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8b1c7fc9d7f3d93a41a2ddb57fc3bb28_l3.png)
b/ Montrons que ![]() possède deux points critiques
possède deux points critiques ![]() et
et ![]() . Pour ce faire, on désigne par
. Pour ce faire, on désigne par ![]() l’ensemble des points critiques de
l’ensemble des points critiques de ![]() . Par des calculs simples, on trouve que :
. Par des calculs simples, on trouve que :
![Rendered by QuickLaTeX.com \[\qquad \quadx\in \mathcal{C} \quad \Longleftrightarrow \quad \nabla(f)(x)=(0,...,0) \quad \Longleftrightarrow \quad\left \{\begin{array}{cll}\left(1-2x_1 \displaystyle\sum_{k=1}^n x_k\right)\exp\left(-\displaystyle\sum_{k=1}^n x_k^2\right) & = & 0 \\\vdots & & \\\left(1-2x_n \displaystyle\sum_{k=1}^n x_k\right)\exp\left(-\displaystyle\sum_{k=1}^n x_k^2\right) & = & 0\end{array}\right. .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9eab593af11ad2842256bf2a143a89e4_l3.png)
Comme toute exponentielle d’un nombre réel est ![]() (et donc non nulle), on obtient que :
(et donc non nulle), on obtient que :
![Rendered by QuickLaTeX.com \[x\in \mathcal{C} \quad \Longleftrightarrow \quad\left \{\begin{array}{cll}1-2x_1 \displaystyle\sum_{k=1}^n x_k & = & 0 \\\vdots & & \\1-2x_n \displaystyle\sum_{k=1}^n x_k & = & 0\end{array}\right. .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a8eb9b037e1c740ad2b04778d597ef27_l3.png)
Comme ![]() , la somme
, la somme ![]() est non nulle, et donc :
est non nulle, et donc :
![Rendered by QuickLaTeX.com \[x\in \mathcal{C} \quad \Longleftrightarrow \quad\left \{\begin{array}{clc}x_1 & = & \frac{1}{2\sum_{k=1}^n x_k} \\\vdots & & \vdots \\x_n & = & \frac{1}{2\sum_{k=1}^n x_k}\end{array}\right. .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-df8dc1d559434810c0c1e5d2220e7b1c_l3.png)
En effectuant les opérations élémentaires
![Rendered by QuickLaTeX.com \[x\in \mathcal{C} \quad \Longleftrightarrow \quad\left \{\begin{array}{clc}x_1 & = & \frac{1}{2\sum_{k=1}^n x_k} \\x_2 & = & x_1 \\\vdots & & \vdots \\x_n & = & x_1\end{array}\right. .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1b573eb95a2e73d8d5582a5714162b9c_l3.png)
En effectuant une substitution dans la première égalité, on trouve que :
![Rendered by QuickLaTeX.com \[x\in \mathcal{C} \quad \Longleftrightarrow \quad\left \{\begin{array}{clc}x_1 & = & \frac{1}{2nx_1} \\x_2 & = & x_1 \\\vdots & & \vdots \\x_n & = & x_1\end{array}\right. \quad \Longleftrightarrow \quad\left \{\begin{array}{clc}x_1 ^2 & = & \frac{1}{2n} \\x_2 & = & x_1 \\\vdots & & \vdots \\x_n & = & x_1\end{array}\right. .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b56e5b42107ba2f43af9332265e27353_l3.png)
Dès lors, on obtient par des calculs simples que :
![Rendered by QuickLaTeX.com \[x\in \mathcal{C} \quad \Longleftrightarrow \quad\left \{\begin{array}{clc}x_1 & = & \frac{1}{\sqrt{2n}} \\x_2 & = & \frac{1}{\sqrt{2n}} \\\vdots & & \vdots \\x_n & = & \frac{1}{\sqrt{2n}} \end{array}\right.\quad \text{ou} \quad\left \{\begin{array}{clc}x_1 & = & \frac{-1}{\sqrt{2n}} \\x_2 & = & \frac{-1}{\sqrt{2n}} \\\vdots & & \vdots \\x_n & = & \frac{-1}{\sqrt{2n}} \end{array}\right. .\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3159589fe4f8c251e9f8669f6e637139_l3.png)
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{f \text{ admet deux points critiques, à savoir les points } a = \frac{1}{\sqrt{2n}}(1,1,\dots,1) \text{ et } b = -a.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-fd46ca57b59c30c90952a83b0f0748a5_l3.png)
3/ a/ Déterminons les dérivées partielles d’ordre ![]() de
de ![]() . Pour ce faire, on distingue les cas »
. Pour ce faire, on distingue les cas » ![]() » et »
» et » ![]() « . Si
« . Si ![]() , alors on trouve par des calculs simples que, pour tout
, alors on trouve par des calculs simples que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\qquad \quad \begin{array}{lll}\partial_{i,i} ^2(f_n)(x) &= & \displaystyle \partial_{i} \left(\left [1-2x_i\sum_{k=1}^n x_k\right ]\exp\left(-\sum_{k=1}^n x_k^2\right)\right ) \\& & \\& = & \displaystyle \partial_{i} \left(1-2x_i\sum_{k=1}^n x_k\right ) \exp\left(-\sum_{k=1}^n x_k^2\right) + \left [1-2x_i\sum_{k=1}^n x_k\right ]\partial_{i} \left(\exp\left(-\sum_{k=1}^n x_k^2\right)\right )\\& & \\& = & \displaystyle \left(-2\sum_{k=1}^n x_k-2x_i\right ) \exp\left(-\sum_{k=1}^n x_k^2\right) + \left [1-2x_i\sum_{k=1}^n x_k\right ]\left [-2x_i\exp\left(-\sum_{k=1}^n x_k^2\right)\right ]\\& & \\& = & \displaystyle \left(-2\sum_{k=1}^n x_k-2x_i\right ) \exp\left(-\sum_{k=1}^n x_k^2\right) + \left (-2x_i +4x_i^2\sum_{k=1}^n x_k\right )\exp\left(-\sum_{k=1}^n x_k^2\right)\\& & \\& = & \displaystyle \left(-2\sum_{k=1}^n x_k-2x_i-2x_i +4x_i^2\sum_{k=1}^n x_k\right ) \exp\left(-\sum_{k=1}^n x_k^2\right) \\& & \\& = & \displaystyle \left(-4x_i +(4x_i^2 -2) \sum_{k=1}^n x_k\right ) \exp\left(-\sum_{k=1}^n x_k^2\right). \\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d6bc8bd6d97cae03bab3309b5a63624b_l3.png)
Si maintenant ![]() , alors on obtient de même que, pour tout
, alors on obtient de même que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\qquad \quad \begin{array}{lll}\partial_{i,j} ^2(f_n)(x) &= & \displaystyle \partial_{i} \left(\left [1-2x_j\sum_{k=1}^n x_k\right ]\exp\left(-\sum_{k=1}^n x_k^2\right)\right ) \\& & \\& = & \displaystyle \partial_{i} \left(1-2x_j\sum_{k=1}^n x_k\right ) \exp\left(-\sum_{k=1}^n x_k^2\right) + \left [1-2x_j\sum_{k=1}^n x_k\right ]\partial_{i} \left(\exp\left(-\sum_{k=1}^n x_k^2\right)\right )\\& & \\& = & \displaystyle -2x_j\exp\left(-\sum_{k=1}^n x_k^2\right) + \left [1-2x_j\sum_{k=1}^n x_k\right ]\left [-2x_i\exp\left(-\sum_{k=1}^n x_k^2\right)\right ]\\& & \\& = & \displaystyle -2x_j \exp\left(-\sum_{k=1}^n x_k^2\right) + \left (-2x_i +4x_ix_j\sum_{k=1}^n x_k\right )\exp\left(-\sum_{k=1}^n x_k^2\right)\\& & \\& = & \displaystyle \left(-2x_j-2x_i +4x_ix_j \sum_{k=1}^n x_k\right ) \exp\left(-\sum_{k=1}^n x_k^2\right). \\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b4b4945e28d491fea754aff36dbe39c4_l3.png)
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{\partial_{i,j} ^2(f_n)(x)=\left \{\begin{array}{lll}\displaystyle \left(-4x_i +(4x_i^2 -2) \sum_{k=1}^n x_k\right ) \exp\left(-\sum_{k=1}^n x_k^2\right) & \text{si} & i=j\\& & \\\displaystyle \left(-2x_j-2x_i +4x_ix_j \sum_{k=1}^n x_k\right ) \exp\left(-\sum_{k=1}^n x_k^2\right) & \text{si} & i\not=j\end{array}\right. .}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7d8dc62b84aa64aaf9958aadfdf3beec_l3.png)
b/ Vérifions que la hessienne de ![]() en
en ![]() est
est ![]() . Par définition, la hessienne en
. Par définition, la hessienne en ![]() est la matrice de terme général
est la matrice de terme général ![]() . Avec la question précédente et comme
. Avec la question précédente et comme ![]() , on trouve si
, on trouve si ![]() que :
que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\partial_{i,i} ^2(f_n)(a) & = & \displaystyle \left(-4a_i +(4a_i^2 -2) \sum_{k=1}^n a_k\right ) \exp\left(-\sum_{k=1}^n a_k^2\right) \\& & \\& = & \displaystyle \left(-\frac{4}{\sqrt{2n}} +\left (4\left ( \frac{1}{\sqrt{2n}}\right )^2 -2 \right ) \sum_{k=1}^n \frac{1}{\sqrt{2n}}\right ) \exp\left(-\sum_{k=1}^n \left (\frac{1}{\sqrt{2n}}\right )^2\right) \\& & \\& = & \displaystyle \left(-\frac{4}{\sqrt{2n}} +\left (\frac{2}{n} -2 \right ) \frac{n}{\sqrt{2n}}\right ) \exp\left(-\sum_{k=1}^n \frac{1}{2n}\right) \\& & \\& = & \displaystyle \left(-\frac{4}{\sqrt{2n}} +\left (2 -2n \right ) \frac{1}{\sqrt{2n}}\right ) \exp\left(-\frac{1}{2}\right) \\& & \\& = & \displaystyle -\frac{(2+2n)}{\sqrt{2n}}\exp\left(-\frac{1}{2}\right) \\& & \\& = & \displaystyle -\frac{(2+2n)}{\sqrt{2ne}}. \\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-dd61cf0c968dec0b3290c09101d619da_l3.png)
Si maintenant
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\partial_{i,j} ^2(f_n)(a) & = & \displaystyle \left(-2a_j-2a_i +4a_ia_j \sum_{k=1}^n a_k\right ) \exp\left(-\sum_{k=1}^n a_k^2\right) \\& & \\& = & \displaystyle \left(-\frac{2}{\sqrt{2n}}-\frac{2}{\sqrt{2n}} +4\left ( \frac{1}{\sqrt{2n}}\right )^2 \sum_{k=1}^n \frac{1}{\sqrt{2n}}\right ) \exp\left(-\sum_{k=1}^n \left ( \frac{1}{\sqrt{2n}}\right )^2\right) \\& & \\& = & \displaystyle \left(-\frac{4}{\sqrt{2n}}+\frac{2}{n} \times \frac{n}{\sqrt{2n}}\right ) \exp\left(-\sum_{k=1}^n \frac{1}{2n}\right) \\& & \\& = & \displaystyle \left(-\frac{4}{\sqrt{2n}}+\frac{2}{\sqrt{2n}}\right ) \exp\left(-\frac{1}{2}\right) \\& & \\& = & \displaystyle -\frac{2}{\sqrt{2n}} \exp\left(-\frac{1}{2}\right) \\& & \\& = & \displaystyle -\frac{2}{\sqrt{2ne}}. \\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ff398878c0473ce4edb9758b7ab46368_l3.png)
Dès lors, la matrice hessienne ![]() est donnée par la matrice :
est donnée par la matrice :
![Rendered by QuickLaTeX.com \[H_n(a)=\begin{pmatrix}-\frac{(2+2n)}{\sqrt{2ne}} & & (-\frac{2}{\sqrt{2ne}} )\\& \ddots & \\(-\frac{2}{\sqrt{2ne}} )& & -\frac{(2+2n)}{\sqrt{2ne}}\end{pmatrix}, \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-58b8cfc8f66bc8607981be68ca3dfb69_l3.png)
ce que l’on peut encore réécrire sous la forme :
![Rendered by QuickLaTeX.com \[H_n(a)=-\frac{2}{\sqrt{2ne}} \begin{pmatrix}1 & ... & 1 \\\vdots & & \vdots \\1 & ... & 1 \\\end{pmatrix}-\frac{2n}{\sqrt{2ne}} \begin{pmatrix}1 & & (0) \\& \ddots & \\(0) & & 1\end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1f0101f32d113c5686053b20ee64e30d_l3.png)
Par conséquent, on en déduit par définition de ![]() que :
que :
![Rendered by QuickLaTeX.com \[\boxed{H_n(a)=\frac{-2}{\sqrt{2ne}} (nI_n + J_n).}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a4d2c6d3fdfe804c297f340622dbc6d1_l3.png)
c/ Donnons les valeurs propres de ![]() . Pour ce faire, considérons un nombre complexe
. Pour ce faire, considérons un nombre complexe ![]() . Alors on trouve avec les questions précédentes que :
. Alors on trouve avec les questions précédentes que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\lambda \in \text{Sp}(H_n(a)) & \Longleftrightarrow & \rm{rg}(H_n(a)-\lambda I_n)<n \\& & \\& \Longleftrightarrow & \displaystyle \rm{rg}\left (\frac{-2}{\sqrt{2ne}} (nI_n + J_n) -\lambda I_n \right )<n \\& & \\& \Longleftrightarrow & \displaystyle \rm{rg}\left (nI_n + J_n +\frac{\lambda\sqrt{2ne}}{2} I_n \right )<n \\& & \\& \Longleftrightarrow & \displaystyle \rm{rg}\left (J_n -\left (-n-\frac{\lambda\sqrt{2ne}}{2} \right ) I_n \right )<n \\& & \\& \Longleftrightarrow & \displaystyle \left (-n-\frac{\lambda\sqrt{2ne}}{2} \right ) \in \text{Sp}(J_n) \\& & \\& \Longleftrightarrow & \displaystyle -n-\frac{\lambda\sqrt{2ne}}{2}=0 \; \; \text{ou} \; \; -n-\frac{\lambda\sqrt{2ne}}{2}=n \\& & \\& \Longleftrightarrow & \displaystyle \lambda = -\sqrt{\frac{2n}{e}} \; \; \text{ou} \; \; \lambda =-2\sqrt{\frac{2n}{e}}. \\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-809ca9634d357cab71751c603e7b290e_l3.png)
Par conséquent, on en déduit par définition de ![]() que :
que :
![Rendered by QuickLaTeX.com \[\boxed{\text{Sp}(H_n(a))=\left \{-2\sqrt{\frac{2n}{e}},-\sqrt{\frac{2n}{e}} \right \}.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e54747a16f4b472f84e95dbdde13e341_l3.png)
d/ Montrons que ![]() possède un extremum local en
possède un extremum local en ![]() . D’après les questions précédentes, on voit que
. D’après les questions précédentes, on voit que ![]() est un point critique de
est un point critique de ![]() et que la hessienne de
et que la hessienne de ![]() au point
au point ![]() n’admet que des valeurs propres
n’admet que des valeurs propres ![]() . D’après le cours, on en déduit que :
. D’après le cours, on en déduit que :
![]()
e/ Donnons une conclusion concernant le point critique ![]() . En procédant comme dans les questions précédentes, on peut vérifier que que la hessienne de
. En procédant comme dans les questions précédentes, on peut vérifier que que la hessienne de ![]() au point
au point ![]() n’admet que des valeurs propres
n’admet que des valeurs propres ![]() . Comme
. Comme ![]() est un point critique de
est un point critique de ![]() , on en déduit d’après le cours que :
, on en déduit d’après le cours que :
![]()
4/ a/ Étudions la fonction ![]() qui, à tout
qui, à tout ![]() de
de ![]() , associe
, associe ![]() . Par définition, la fonction
. Par définition, la fonction ![]() est dérivable sur
est dérivable sur ![]() comme produit et composée de fonctions dérivables sur
comme produit et composée de fonctions dérivables sur ![]() et de plus, on a pour tout
et de plus, on a pour tout ![]() :
:
![]()
Comme ![]() et que
et que ![]() , on constate que
, on constate que ![]() si et seulement si
si et seulement si ![]() , c’est-à-dire si
, c’est-à-dire si ![]() . Dès lors, la fonction
. Dès lors, la fonction ![]() est croissante sur
est croissante sur ![]() et décroissante sur
et décroissante sur ![]() . Comme de plus
. Comme de plus ![]() tend vers
tend vers ![]() quand
quand ![]() tend vers
tend vers ![]() par croissances comparées, on en déduit le tableau de variations suivant pour
par croissances comparées, on en déduit le tableau de variations suivant pour ![]() :
:
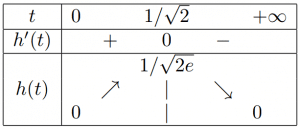
b/ En appliquant l’inégalité de Cauchy-Schwarz à deux vecteurs bien choisis de ![]() , muni de son produit scalaire canonique, montrer que :
, muni de son produit scalaire canonique, montrer que :
![Rendered by QuickLaTeX.com \[\forall (x_1,x_2,\dots,x_n) \in \mathbb{R}^n, \, \left(\sum_{k=1}^n x_k\right)^2 \leq n \sum_{k=1}^n x_k^2.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d2a7b5bcf58576862a00fc4c4a0dfc6e_l3.png)
Pour ce faire, on désigne par
![Rendered by QuickLaTeX.com \[\left(\sum_{k=1}^n x_k\right)^2=\left (\langle x,u\rangle\right )^2\leq \|x\|^2\|u\|^2=\left ( \sum_{k=1}^n x_k^2 \right )\left ( \sum_{k=1}^n 1^2\right )=n\left ( \sum_{k=1}^n x_k^2 \right ).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-92a5aeb12b69b6a119ae9ff15cd94d95_l3.png)
Par conséquent, on en déduit que, pour tout
![Rendered by QuickLaTeX.com \[\boxed{\left(\sum_{k=1}^n x_k\right)^2 \leq n \sum_{k=1}^n x_k^2.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-21231996c7c105d1e5af70e8eb498559_l3.png)
c/ Montrons que ![]() admet en
admet en ![]() un extremum global. D’après les questions précédentes, on trouve par des calculs simples que :
un extremum global. D’après les questions précédentes, on trouve par des calculs simples que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}f_n(a) &= & \displaystyle \left (\sum_{k=1}^n a_k\right )\exp\left(-\sum_{k=1}^n a_k^2\right) \\& & \\& = & \displaystyle \left (\sum_{k=1}^n \frac{1}{\sqrt{2n}} \right )\exp\left(-\sum_{k=1}^n \left ( \frac{1}{\sqrt{2n}} \right )^2\right) \\& & \\& = & \displaystyle \frac{n}{\sqrt{2n}}\exp\left(-\sum_{k=1}^n \frac{1}{2n}\right) \\& & \\& = & \displaystyle \frac{\sqrt{n}}{\sqrt{2}}\exp\left(-\frac{1}{2}\right) \quad = \quad \sqrt{\frac{n}{2e}}.\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5f3c3f0a7ce8235e519129de86baad5a_l3.png)
De plus, on trouve d’après la question précédente que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[f_n(x)=\left (\sum_{k=1}^n x_k\right )\exp\left(-\sum_{k=1}^n x_k^2\right)\leq \sqrt{n} \sqrt{\sum_{k=1}^n x_k ^2 }\exp\left(-\sum_{k=1}^n x_k^2\right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d369ff5f319c3cdffe61566956aed1b6_l3.png)
Si l’on pose ![]() , alors ceci nous donne que :
, alors ceci nous donne que :
![]()
Or on sait d’après son tableau de variations que la fonction ![]() admet un maximum sur
admet un maximum sur ![]() , lequel est atteint en
, lequel est atteint en ![]() et vaut
et vaut ![]() . En particulier, on voit que
. En particulier, on voit que ![]() pour tout
pour tout ![]() , ce qui entraine que :
, ce qui entraine que :
![]()
En résumé, on vient de montrer que ![]() pour tout
pour tout ![]() , avec égalité si
, avec égalité si ![]() , et donc :
, et donc :
![]()
De la même façon, on vérifie aussi que :
![]()
5/ Question d’informatique.
a/ Écrivons des commandes Scilab permettant de calculer et d’afficher ![]() pour une valeur de
pour une valeur de ![]() entrée par l’utilisateur. D’après les questions précédentes, on sait que :
entrée par l’utilisateur. D’après les questions précédentes, on sait que :
![]()
Dès lors, on pourra utiliser le script suivant :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{l}n=\text{input('entrez un entier n :')}\; ; \\A=(-2/\text{sqrt}(2*n*\exp(1)))*(\text{ones}(n,n)+n*\text{eye}(n))\; ; \\\text{disp}(A)\\\end{array}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-426149241d65f93529a1d8ebebb3fd55_l3.png)
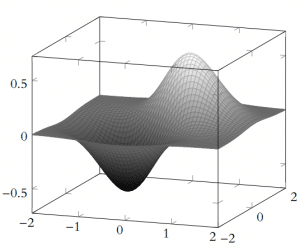
b/ Dans le cas ![]() , la nappe suivante est acceptable en tant que représentation graphique de la fonction
, la nappe suivante est acceptable en tant que représentation graphique de la fonction ![]() . En effet, comme cela a été montré aux questions précédentes, le graphe de
. En effet, comme cela a été montré aux questions précédentes, le graphe de ![]() (comme c’est le cas pour cette nappe) présente un maximum global et un minimum global, lesquels sont atteints en des points opposés par rapport à l’origine de
(comme c’est le cas pour cette nappe) présente un maximum global et un minimum global, lesquels sont atteints en des points opposés par rapport à l’origine de ![]() .
.
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Problème 1 : Intégrale de Wallis
Partie 1 : Simulations de  et
et 
1/ Complétons les lignes ![]() et
et ![]() du script Scilab suivant pour qu’il affiche la valeur prise par
du script Scilab suivant pour qu’il affiche la valeur prise par ![]() lorsque
lorsque ![]() et
et ![]() sont entrés par l’utilisateur :
sont entrés par l’utilisateur :
![Rendered by QuickLaTeX.com \[\boxed{\begin{tabular}{l}k = input('donnez une valeur pour k :') \\p = input('donnez une valeur pour p :') \\n = 0 \\c = 0 \\while c \operatorname{<} k \\\qquad n=n+1 \\\qquad if - - - then c = c+1 \\\qquad end \\end \\disp(- - -) \\\end{tabular}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ce7ed9f09ba3be7b154449074e34e775_l3.png)
Dans ce script, ![]() correspond au nombre de lancers effectués et
correspond au nombre de lancers effectués et ![]() au nombre de piles obtenus au cours des
au nombre de piles obtenus au cours des ![]() premiers lancers. Dans ce cas, pour que l’on passe de
premiers lancers. Dans ce cas, pour que l’on passe de ![]() à
à ![]() dans la boucle « while », il faut et il suffit que le résultat du
dans la boucle « while », il faut et il suffit que le résultat du ![]() -ème lancer soit un pile, ce qui peut se simuler par l’instruction «
-ème lancer soit un pile, ce qui peut se simuler par l’instruction « ![]() » (vu que la pièce a une probabilité
» (vu que la pièce a une probabilité ![]() de donner pile à chaque fois). Quant à la valeur de
de donner pile à chaque fois). Quant à la valeur de ![]() , elle correspond au nombre de fois que la boucle « while » aura tourné, c’est-à-dire à
, elle correspond au nombre de fois que la boucle « while » aura tourné, c’est-à-dire à ![]() . Dès lors, on pourra compléter le script ci-dessus comme suit :
. Dès lors, on pourra compléter le script ci-dessus comme suit :
![Rendered by QuickLaTeX.com \[\boxed{\begin{tabular}{l}k = input('donnez une valeur pour k :') \\p = input('donnez une valeur pour p :') \\n = 0 \\c = 0 \\while c \operatorname{<} k \\\qquad n=n+1 \\\qquad if rand \operatorname{<} p \: then c = c+1 \\\qquad end \\end \\disp(n) \\\end{tabular}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2cb7dbc7dd0677cd28698b4381429667_l3.png)
2/ On souhaite que le script précédent affiche la valeur prise par ![]() . Il s’agit alors de remplacer la ligne
. Il s’agit alors de remplacer la ligne ![]() du script précédent par la suivante, dûment complétée :
du script précédent par la suivante, dûment complétée :
![]()
Dans ce nouveau script, l’entier ![]() correspond toujours au nombre de lancers effectués. Par contre, l’entier
correspond toujours au nombre de lancers effectués. Par contre, l’entier ![]() est égal au nombre de piles de la dernière série de piles obtenus si le
est égal au nombre de piles de la dernière série de piles obtenus si le ![]() -ème lancer donne un pile, et à
-ème lancer donne un pile, et à ![]() sinon. Dans ce cas, pour que l’on passe de
sinon. Dans ce cas, pour que l’on passe de ![]() à
à ![]() dans la boucle « while », il faut et il suffit que le résultat du
dans la boucle « while », il faut et il suffit que le résultat du ![]() -ème lancer soit un pile, ce qui peut se simuler par l’instruction «
-ème lancer soit un pile, ce qui peut se simuler par l’instruction « ![]() » (vu que la pièce a une probabilité
» (vu que la pièce a une probabilité ![]() de donner pile à chaque fois). En revanche, si le
de donner pile à chaque fois). En revanche, si le ![]() -ème lancer donne un face, alors
-ème lancer donne un face, alors ![]() est réinitialisé à
est réinitialisé à ![]() , ce qui signifie que les
, ce qui signifie que les ![]() premiers lancers ne se terminent pas par une série de piles. Dans ces conditions, la boucle « while » s’interrompra si
premiers lancers ne se terminent pas par une série de piles. Dans ces conditions, la boucle « while » s’interrompra si ![]() , c’est-à-dire si les
, c’est-à-dire si les ![]() lancers se terminent par une série de
lancers se terminent par une série de ![]() piles consécutifs. Quant à la valeur de
piles consécutifs. Quant à la valeur de ![]() , elle correspondra au nombre de fois que la boucle « while » aura tourné, c’est-à-dire à
, elle correspondra au nombre de fois que la boucle « while » aura tourné, c’est-à-dire à ![]() . Dès lors, pour obtenir une simulation de
. Dès lors, pour obtenir une simulation de ![]() , il suffit de compléter la ligne
, il suffit de compléter la ligne ![]() ci-dessus comme suit :
ci-dessus comme suit :
![]()
Partie 2 : Calcul de l’espérance de 
1/ Donner la loi de ![]() ainsi que son espérance. Par définition, on sait que
ainsi que son espérance. Par définition, on sait que ![]() est le nombre de lancers qu’il faut réaliser pour obtenir pour la première fois un pile. Plus précisément, on répète indéfiniment et dans les mêmes conditions une expérience de Bernoulli, qui consiste à lancer la pièce de monnaie et où la probabilité du succès (à savoir l’obtention d’un pile) à chaque itération est égale à
est le nombre de lancers qu’il faut réaliser pour obtenir pour la première fois un pile. Plus précisément, on répète indéfiniment et dans les mêmes conditions une expérience de Bernoulli, qui consiste à lancer la pièce de monnaie et où la probabilité du succès (à savoir l’obtention d’un pile) à chaque itération est égale à ![]() . Comme
. Comme ![]() est le premier instant o\`u le succès est réalisé,
est le premier instant o\`u le succès est réalisé, ![]() est un temps d’arrêt et suit donc la loi géométrique de paramètre
est un temps d’arrêt et suit donc la loi géométrique de paramètre ![]() , c’est-à-dire :
, c’est-à-dire :
![]()
D’après le cours, comme ![]() , on a :
, on a :
![Rendered by QuickLaTeX.com \[ \boxed{E(X_1)= \frac{1}{p}.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5d9cbeeaba4306cacc5ee121ced5dcf1_l3.png)
2/ Soit ![]() un entier naturel
un entier naturel ![]() . Pour tout entier naturel
. Pour tout entier naturel ![]() , on note
, on note ![]() la variable aléatoire égale au nombre de piles obtenus lors des
la variable aléatoire égale au nombre de piles obtenus lors des ![]() premiers lancers.
premiers lancers.
a/ Donnons la loi de ![]() . Pour ce faire, on considère l’expérience aléatoire suivante « on lance la pièce », laquelle présente deux issues, à savoir
. Pour ce faire, on considère l’expérience aléatoire suivante « on lance la pièce », laquelle présente deux issues, à savoir ![]() : « on obtient pile » et
: « on obtient pile » et ![]() : « on obtient face ». On répète cette expérience
: « on obtient face ». On répète cette expérience ![]() fois de suite et dans les mêmes conditions. Comme la probabilité de l’issue
fois de suite et dans les mêmes conditions. Comme la probabilité de l’issue ![]() est égale à
est égale à ![]() à chaque lancer et que
à chaque lancer et que ![]() est le nombre de succès de l’issue
est le nombre de succès de l’issue ![]() , on en déduit que :
, on en déduit que :
![]()
b/ Donnons tout d’abord ![]() . Par définition,
. Par définition, ![]() est le nombre de lancers qu’il faut réaliser pour obtenir
est le nombre de lancers qu’il faut réaliser pour obtenir ![]() piles. Donc
piles. Donc ![]() ne peut prendre que des valeurs entières
ne peut prendre que des valeurs entières ![]() . De plus, on voit que
. De plus, on voit que ![]() ne peut prendre la valeur entière
ne peut prendre la valeur entière ![]() que si
que si ![]() (il faut réaliser au moins
(il faut réaliser au moins ![]() lancers pour avoir
lancers pour avoir ![]() piles) et l’événement
piles) et l’événement ![]() est réalisé si, par exemple, on n’obtient que des faces au cours des
est réalisé si, par exemple, on n’obtient que des faces au cours des ![]() premiers lancers, puis
premiers lancers, puis ![]() piles après. En d’autres termes,
piles après. En d’autres termes, ![]() peut prendre toute valeur entière
peut prendre toute valeur entière ![]() , et donc :
, et donc :
![]()
A présent, écrivons l’événement ![]() à l’aide de la variable
à l’aide de la variable ![]() . Par définition, l’événement
. Par définition, l’événement ![]() est réalisé si et seulement si l’on a obtenu
est réalisé si et seulement si l’on a obtenu ![]() piles au cours des
piles au cours des ![]() premiers lancers et pile au
premiers lancers et pile au ![]() -ème lancer, c’est-à-dire si les événements
-ème lancer, c’est-à-dire si les événements ![]() et
et ![]() sont simultanément réalisés, et donc :
sont simultanément réalisés, et donc :
![]()
c/ Montrons que la loi de ![]() est donnée par :
est donnée par :
![]()
D’après la formule des probabilités composées et la question précédente, on sait que ![]() et plus, on a pour
et plus, on a pour ![]() :
:
![]()
Comme
![]()
Comme tous les lancers sont indépendants les uns des autres, on voit que :
![]()
En réinjectant cette égalité dans la relation ![]() , il s’ensuit que, pour tout
, il s’ensuit que, pour tout ![]() :
:
![]()
Par conséquent, on en déduit que la loi de ![]() est donnée par :
est donnée par :
![Rendered by QuickLaTeX.com \[ \boxed{\forall n\geq k, \; \; P([S_k=n])=\binom{n-1}{k-1} p^{k}q^{n-k}.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a13995e56647d100c78a26f6a7af07a9_l3.png)
3/ Soit ![]() un entier
un entier ![]() . On pose
. On pose ![]() et, pour tout entier
et, pour tout entier ![]() , on pose
, on pose ![]() . On admet que
. On admet que ![]() est une suite de variables aléatoires mutuellement indépendantes.
est une suite de variables aléatoires mutuellement indépendantes.
a/ Donnons la loi des variables aléatoires ![]() . Par définition,
. Par définition, ![]() désigne le temps d’attente entre le
désigne le temps d’attente entre le ![]() -ème pile et le
-ème pile et le ![]() -ème pile (voire le temps d’attente du premier pile si
-ème pile (voire le temps d’attente du premier pile si ![]() ). Comme les résultats des lancers sont indépendants et que la probabilité d’obtenir pile est égale à
). Comme les résultats des lancers sont indépendants et que la probabilité d’obtenir pile est égale à ![]() à chaque lancer, on en déduit que, pour tout
à chaque lancer, on en déduit que, pour tout ![]() :
:
![]()
b/ Exprimons ![]() à l’aide de certaines des variables
à l’aide de certaines des variables ![]() . Comme
. Comme ![]() et que
et que ![]() pour tout entier
pour tout entier ![]() , on obtient par télescopage que :
, on obtient par télescopage que :
![Rendered by QuickLaTeX.com \[\sum_{i=1}^k Z_i=Z_1+\sum_{i=2}^k S_i - S_{i-1}=S_1+S_k-S_1=S_k.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-283c14d8860b2278fb323284b94e19b4_l3.png)
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{S_k=\sum_{i=1}^k Z_i.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-acd826e51803f0058acf0bd163e4b470_l3.png)
c/ Montrons que ![]() possède une espérance et donnons sa valeur. Comme les
possède une espérance et donnons sa valeur. Comme les ![]() suivent toutes la loi géométrique de paramètre
suivent toutes la loi géométrique de paramètre ![]() d’après la question
d’après la question ![]() , elles admettent toutes une espérance égale à
, elles admettent toutes une espérance égale à ![]() . Dès lors, comme
. Dès lors, comme ![]() d’après la question
d’après la question ![]() , la variable aléatoire
, la variable aléatoire ![]() admet aussi une espérance par linéarité et de plus, on obtient par linéarité de l’espérance que :
admet aussi une espérance par linéarité et de plus, on obtient par linéarité de l’espérance que :
![Rendered by QuickLaTeX.com \[E(S_k)=E\left ( \sum_{i=1}^k Z_i\right )=\sum_{i=1}^k E(Z_i)=\sum_{i=1}^k \frac{1}{p}=\frac{k}{p}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0f3b92fd3ab426cd26a00fa72e18094c_l3.png)
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{S_k \text{ admet une esp\'erance \'egale \`a } \frac{k}{p}.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-40e65723828161457de16c57c7e7b9ab_l3.png)
4/ Estimation. On suppose le paramètre ![]() inconnu et on souhaite trouver un estimateur de
inconnu et on souhaite trouver un estimateur de ![]() . On admet que, si une suite de variables aléatoires
. On admet que, si une suite de variables aléatoires ![]() converge en probabilité vers une variable aléatoire
converge en probabilité vers une variable aléatoire ![]() , alors pour toute fonction
, alors pour toute fonction ![]() continue sur un intervalle
continue sur un intervalle ![]() de
de ![]() tel que
tel que ![]() , la suite
, la suite ![]() converge en probabilité vers
converge en probabilité vers ![]() .
.
a/ Pour tout ![]() , on pose
, on pose ![]() . Montrons que la suite
. Montrons que la suite ![]() converge en probabilité. D’après la question
converge en probabilité. D’après la question ![]() , on sait que toutes les variables aléatoires
, on sait que toutes les variables aléatoires ![]() suivent la loi géométrique de paramètre
suivent la loi géométrique de paramètre ![]() , laquelle admet une espérance (égale à
, laquelle admet une espérance (égale à ![]() ) et une variance. Comme elles sont de plus indépendantes, la loi faible des grands nombres entraine que leur moyenne empirique
) et une variance. Comme elles sont de plus indépendantes, la loi faible des grands nombres entraine que leur moyenne empirique ![]() converge en probabilité vers l’espérance commune des
converge en probabilité vers l’espérance commune des ![]() , c’est-à-dire
, c’est-à-dire ![]() . Par conséquent, on en déduit que :
. Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[\boxed{\overline{Z_k} \overset{P}{\longrightarrow} \frac1p.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b32717090a5d10d59c14f20711e06d90_l3.png)
b/ Montrons que ![]() est un estimateur convergent de
est un estimateur convergent de ![]() . Pour ce faire, on considère l’application
. Pour ce faire, on considère l’application ![]() ,
, ![]() . Alors
. Alors ![]() est une fonction continue sur l’intervalle
est une fonction continue sur l’intervalle ![]() . Comme la variable aléatoire constante égale à
. Comme la variable aléatoire constante égale à ![]() vérifie la relation
vérifie la relation ![]() (vu que
(vu que ![]() ) et que la suite
) et que la suite ![]() converge en probabilité vers
converge en probabilité vers ![]() , ceci entraine avec le résultat donné plus haut que :
, ceci entraine avec le résultat donné plus haut que :
![]()
Mais comme
![]()
Par conséquent, on en déduit par définition de la convergence des estimateurs que :
![Rendered by QuickLaTeX.com \[\boxed{\frac{k}{S_k} \text{ est un estimateur convergent de }p.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0442633d817e1fa0212f9f9873c3cada_l3.png)
c/ Donnons tout d’abord la valeur de ![]() . Comme
. Comme ![]() d’après la question
d’après la question ![]() , la famille
, la famille ![]() est le système complet d’événements associé à
est le système complet d’événements associé à ![]() . En particulier, on obtient en passant aux probabilités que :
. En particulier, on obtient en passant aux probabilités que :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{j=k-1}^{+\infty} P(S_{k-1} = j)=1.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-216820baac9e7ec6e80e4af6aeb2dff9_l3.png)
A présent, montrons que la variable aléatoire
![]()
En particulier, la variable aléatoire ![]() est bornée par
est bornée par ![]() (en valeur absolue). Comme la variable aléatoire constante égale à
(en valeur absolue). Comme la variable aléatoire constante égale à ![]() admet une espérance, il s’ensuit par domination que :
admet une espérance, il s’ensuit par domination que :
![Rendered by QuickLaTeX.com \[\boxed{\frac{k-1}{S_k-1} \text{ admet une esp\'erance}.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cc45fd33eba4f9be0a45edab5e8c2bcf_l3.png)
Passons au calcul de ![]() . D’après le théorème de transfert et la question
. D’après le théorème de transfert et la question ![]() , on trouve que :
, on trouve que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\displaystyle E\left ( \frac{k-1}{S_k-1} \right ) & = & \displaystyle \sum_{n=k}^{+\infty} \frac{k-1}{n-1} P([S_k=n]) \\& & \\&=& \displaystyle \sum_{n=k}^{+\infty} \frac{k-1}{n-1} \binom{n-1}{k-1} p^{k}q^{n-k} \\& & \\&=& \displaystyle \sum_{n=k}^{+\infty} \frac{k-1}{n-1} \frac{(n-1)!}{(k-1)!(n-k)!}p^{k}q^{n-k} \\& & \\&=& \displaystyle \sum_{n=k}^{+\infty} \frac{(n-2)!}{(k-2)!(n-k)!}p^{k}q^{n-k} \\& & \\&=& \displaystyle \sum_{n=k}^{+\infty} \binom{n-2}{k-2}p^{k}q^{n-k} \\& & \\&=& \displaystyle \sum_{n=k}^{+\infty} \binom{n-1-1}{k-1-1}p^{k-1+1}q^{n-1-k+1} \\& & \\&=& \displaystyle p\sum_{n=k}^{+\infty} \binom{n-1-1}{k-1-1}p^{k-1}q^{n-1-k+1} \\& & \\& = & \displaystyle p\sum_{n=k}^{+\infty} P([S_{k-1}=n-1]).\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e699d00ccd5a3bdc6d9623e38e0c0f78_l3.png)
En effectuant le changement d’indices
![Rendered by QuickLaTeX.com \[E\left ( \frac{k-1}{S_k-1} \right )=p\sum_{j=k-1}^{+\infty} P([S_{k-1}=j])=p\times 1=p.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f09cb8aff4f130a67ba5b6f8e2c83673_l3.png)
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{E\left ( \frac{k-1}{S_k-1} \right )=p.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6e21049b2382409f7a4c31323e548d23_l3.png)
d/ Montrons que ![]() est un estimateur biaisé de
est un estimateur biaisé de ![]() (on ne cherchera pas à calculer la valeur de ce biais). Tout d’abord, on commence par remarquer que, comme la variable aléatoire
(on ne cherchera pas à calculer la valeur de ce biais). Tout d’abord, on commence par remarquer que, comme la variable aléatoire ![]() ne prend que des valeurs entières
ne prend que des valeurs entières ![]() d’après la question
d’après la question ![]() , on voit que
, on voit que ![]() , et donc :
, et donc :
![]()
En particulier, la variable aléatoire ![]() est bornée par
est bornée par ![]() (en valeur absolue). Comme la variable aléatoire constante égale à
(en valeur absolue). Comme la variable aléatoire constante égale à ![]() admet une espérance, il s’ensuit par domination que
admet une espérance, il s’ensuit par domination que ![]() admet une espérance, et donc cet estimateur admet bien un biais. Pour montrer qu’il est biaisé, il suffit de vérifier que
admet une espérance, et donc cet estimateur admet bien un biais. Pour montrer qu’il est biaisé, il suffit de vérifier que ![]() . D’après le théorème de transfert, on sait que l’espérance de
. D’après le théorème de transfert, on sait que l’espérance de ![]() est la somme de la série
est la somme de la série ![]() . Or, on trouve que, pour tout
. Or, on trouve que, pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\displaystyle \frac{k-1}{n-1} < \frac{k}{n} & \Longleftrightarrow & n(k-1) < (n-1)k \\& & \\& \Longleftrightarrow & nk -n < nk-k \\& & \\& \Longleftrightarrow & k < n.\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1d70bf5a86643a5d4bd1364ba90541c0_l3.png)
Comme cette inégalité est toujours vraie, on voit que, pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
Par multiplication par
![]()
Par sommation, on trouve que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{n=k+1}^{+\infty}\frac{k-1}{n-1} P([S_k=n]) < \sum_{n=k+1}^{+\infty} \frac{k}{n} P([S_k=n]),\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c749720bd5d17c89e4727632a57b2b4a_l3.png)
ce qui peut se réécrire avec le théorème de transfert sous la forme :
![]()
En particulier, ceci entraîne avec la question précédente que :
![]()
et donc ![]() . Par conséquent, on en déduit que :
. Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{\frac{k}{S_k} \text{ est un estimateur biais\'e de } p.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f7ae6ac6df025582f0f616b52dcb1715_l3.png)
Partie 3 : Calcul de l’espérance de 
1/ Comparons les variables aléatoires ![]() et
et ![]() . Par définition,
. Par définition, ![]() est le rang d’apparition du dernier pile de la première série d’un pile consécutif, c’est-à-dire le rang d’apparition du premier pile, et donc :
est le rang d’apparition du dernier pile de la première série d’un pile consécutif, c’est-à-dire le rang d’apparition du premier pile, et donc :
![]()
2/ Soit ![]() . On admet que
. On admet que ![]() possède une espérance que l’on se propose de déterminer.
possède une espérance que l’on se propose de déterminer.
a/ Justifions, en utilisant la variable aléatoire ![]() égale au rang du premier face lors de l’expérience décrite au début de ce problème, que les événements
égale au rang du premier face lors de l’expérience décrite au début de ce problème, que les événements ![]() et
et ![]() forment un système complet d’événements. Par définition, l’événement
forment un système complet d’événements. Par définition, l’événement ![]() correspond à l’événement « on obtient face au premier lancer », c’est-à-dire à
correspond à l’événement « on obtient face au premier lancer », c’est-à-dire à ![]() . De même, pour tout
. De même, pour tout ![]() , l’événement
, l’événement ![]() correspond à l’événement « on obtient le premier face au
correspond à l’événement « on obtient le premier face au ![]() -ème lancer », c’est-à-dire à
-ème lancer », c’est-à-dire à ![]() . Enfin, l’événement
. Enfin, l’événement ![]() correspond à l’événement « on obtient le premier face après le
correspond à l’événement « on obtient le premier face après le ![]() -ème lancer », c’est-à-dire à
-ème lancer », c’est-à-dire à ![]() . En d’autres termes, il s’agit de montrer que la famille
. En d’autres termes, il s’agit de montrer que la famille ![]() est un système complet d’événements. De toute évidence, ces événements sont deux à deux incompatibles (vu que
est un système complet d’événements. De toute évidence, ces événements sont deux à deux incompatibles (vu que ![]() ne peut pas prendre deux valeurs distinctes en même temps). De plus, comme la famille
ne peut pas prendre deux valeurs distinctes en même temps). De plus, comme la famille ![]() est le système complet d’événements associé à
est le système complet d’événements associé à ![]() , on obtient que :
, on obtient que :
![Rendered by QuickLaTeX.com \[\bigcup_{i=1}^k [W=i] \cup [W>k]=\bigcup_{i=1}^{k} [W=i] \cup \bigcup_{i=k+1}^{+\infty} [W=i]=\bigcup_{i=1}^{+\infty} [W=i]=\Omega. \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-66631cef7298963608ff22a323e46da6_l3.png)
Dès lors, il s’ensuit que la famille ![]() est bien un système complet d’événements, et donc :
est bien un système complet d’événements, et donc :
![Rendered by QuickLaTeX.com \[\boxed{\begin{tabular}{l}les \'ev\`enements $F_1,P_1 \cap F_2,P_1 \cap P_2 \cap F_3,P_1 \cap P_2 \cap P_3 \cap F_4,\dots,P_1\cap \dots \cap P_{k-1} \cap F_k$ \\ et $P_1 \cap \dots \cap P_{k-1} \cap P_k$ forment un syst\`eme complet d'\'ev\`enements. \end{tabular}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-68a22dbe13116fd9fa41e57cbd8e0031_l3.png)
b/ Montrons tout d’abord que, pour tout entier ![]() , on a
, on a ![]() . Pour ce faire, on considère l’événement
. Pour ce faire, on considère l’événement ![]() : « au cours des lancers
: « au cours des lancers ![]() , le rang d’apparition du dernier pile de la première série de
, le rang d’apparition du dernier pile de la première série de ![]() piles consécutifs est égal à
piles consécutifs est égal à ![]() « . Alors on voit que
« . Alors on voit que ![]() , ce qui entraîne que :
, ce qui entraîne que :
![]()
Comme les résultats des lancers sont indépendants et que ![]() est construit à partir des résultats des lancers
est construit à partir des résultats des lancers ![]() , les événements
, les événements ![]() et
et ![]() sont indépendants, et donc :
sont indépendants, et donc :
![]()
Enfin, comme ![]() est réalisé si et seulement si le rang d’apparition du dernier pile de la première série de
est réalisé si et seulement si le rang d’apparition du dernier pile de la première série de ![]() piles consécutifs est égal à
piles consécutifs est égal à ![]() au cours des lancers
au cours des lancers ![]() , tout se passe comme si l’on réalisait
, tout se passe comme si l’on réalisait ![]() lancers (à savoir les lancers
lancers (à savoir les lancers ![]() ) et que l’on s’intéressait au rang d’apparition du dernier pile de la première série de
) et que l’on s’intéressait au rang d’apparition du dernier pile de la première série de ![]() piles consécutifs. Avec ce phénomène de décalage, on obtient que
piles consécutifs. Avec ce phénomène de décalage, on obtient que ![]() , et donc :
, et donc :
![]()
A présent, montrons que l’espérance conditionnelle ![]() est égale à
est égale à ![]() . Par définition de l’espérance conditionnelle et avec la relation ci-dessus, on trouve que :
. Par définition de l’espérance conditionnelle et avec la relation ci-dessus, on trouve que :
![Rendered by QuickLaTeX.com \[E(T_k \vert F_1) = \sum_{n=k} ^{+\infty} n P_{F_1}([T_k=n]) =\sum_{n=k} ^{+\infty} n P([T_k=n-1]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1e94e51b5820ab8db95044187380bca3_l3.png)
En effectuant le changement d’indices ![]() dans la somme de droite ci-dessus, on obtient que :
dans la somme de droite ci-dessus, on obtient que :
![Rendered by QuickLaTeX.com \[E(T_k \vert F_1)=\sum_{n=k} ^{+\infty} n P([T_k=n-1])=\sum_{j=k-1} ^{+\infty} (j+1) P([T_k=j]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-470e5a6732b7850e84d2aa77c08b0875_l3.png)
Comme l’événement ![]() est impossible (vu qu’il faut au moins
est impossible (vu qu’il faut au moins ![]() lancers pour obtenir une série de
lancers pour obtenir une série de ![]() piles consécutifs), on voit que
piles consécutifs), on voit que ![]() , et donc :
, et donc :
![Rendered by QuickLaTeX.com \[E(T_k \vert F_1)=\sum_{j=k-1} ^{+\infty} (j+1) P([T_k=j])=\sum_{j=k} ^{+\infty} (j+1) P([T_k=j]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1be4fb134a9c14910e531c563edb4704_l3.png)
Par linéarité de la somme, ceci nous donne que :
![Rendered by QuickLaTeX.com \[E(T_k \vert F_1)=\sum_{j=k} ^{+\infty} (j+1) P([T_k=j])=\sum_{j=k} ^{+\infty} jP([T_k=j])+\sum_{j=k} ^{+\infty} P([T_k=j]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a6a8a6ccb7e5d8e0d801fe0bd5e9c7e5_l3.png)
Comme la famille ![]() est un système complet d’événements, on constate que la deuxième somme de droite dans l’égalité ci-dessus vaut
est un système complet d’événements, on constate que la deuxième somme de droite dans l’égalité ci-dessus vaut ![]() . Comme on reconnaît dans la première somme de droite l’espérance de
. Comme on reconnaît dans la première somme de droite l’espérance de ![]() , on en déduit que :
, on en déduit que :
![]()
c/ De la même façon, déterminons, pour tout ![]() , la valeur de
, la valeur de ![]() . On commence par montrer que, pour tout entier
. On commence par montrer que, pour tout entier ![]() , on a
, on a ![]() . Pour ce faire, on considère l’événement
. Pour ce faire, on considère l’événement ![]() : » au cours des lancers
: » au cours des lancers ![]() , le rang d’apparition du dernier pile de la première série de
, le rang d’apparition du dernier pile de la première série de ![]() piles consécutifs est égal à
piles consécutifs est égal à ![]() « . Comme
« . Comme ![]() , on voit que
, on voit que ![]() , ce qui entraîne que :
, ce qui entraîne que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}P_{P_1 \cap \dots \cap P_{i-1} \cap F_i}(T_k = n)&=&\displaystyle \frac{P([T_k=n]\cap P_1 \cap \dots \cap P_{i-1} \cap F_i)}{P(P_1 \cap \dots \cap P_{i-1} \cap F_i)} \\& & \\&=& \displaystyle \frac{P(A_{n,k,i}\cap P_1 \cap \dots \cap P_{i-1} \cap F_i)}{P(P_1 \cap \dots \cap P_{i-1} \cap F_i)} \\& & \\& = &\displaystyle P_{P_1 \cap \dots \cap P_{i-1} \cap F_i}(A_{n,k,i}).\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-294287e969420b9f0d7027d877e547e1_l3.png)
Comme les résultats des lancers sont indépendants et que ![]() est construit à partir des résultats des lancers
est construit à partir des résultats des lancers ![]() , les événements
, les événements ![]() et
et ![]() sont indépendants, et donc :
sont indépendants, et donc :
![]()
Enfin, comme ![]() est réalisé si et seulement si le rang d’apparition du dernier pile de la première série de
est réalisé si et seulement si le rang d’apparition du dernier pile de la première série de ![]() piles consécutifs est égal à
piles consécutifs est égal à ![]() au cours des lancers
au cours des lancers ![]() , tout se passe comme si l’on réalisait
, tout se passe comme si l’on réalisait ![]() lancers (à savoir les lancers
lancers (à savoir les lancers ![]() ) et que l’on s’intéressait au rang d’apparition du dernier pile de la première série de
) et que l’on s’intéressait au rang d’apparition du dernier pile de la première série de ![]() piles consécutifs. Avec ce phénomène de décalage, on obtient que
piles consécutifs. Avec ce phénomène de décalage, on obtient que ![]() , et donc :
, et donc :
![]()
A présent, montrons que l’espérance conditionnelle ![]() est égale à
est égale à ![]() . Par définition de l’espérance conditionnelle et avec la relation ci-dessus, on trouve que :
. Par définition de l’espérance conditionnelle et avec la relation ci-dessus, on trouve que :
![Rendered by QuickLaTeX.com \[E(T_k \vert P_1 \cap \dots \cap P_{i-1} \cap F_i) = \sum_{n=k} ^{+\infty} n P_{P_1 \cap \dots \cap P_{i-1} \cap F_i}([T_k=n]) =\sum_{n=k} ^{+\infty} n P([T_k=n-i]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f5d23da12dbccd1c41845bab5af937ec_l3.png)
En effectuant le changement d’indices ![]() dans la somme de droite ci-dessus, on obtient que :
dans la somme de droite ci-dessus, on obtient que :
![Rendered by QuickLaTeX.com \[E(T_k \vert P_1 \cap \dots \cap P_{i-1} \cap F_i)=\sum_{n=k} ^{+\infty} n P([T_k=n-i])=\sum_{j=k-i} ^{+\infty} (j+i) P([T_k=j]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1fd3616f49d27a0f74cc03e98f63420b_l3.png)
Comme les événements ![]() sont impossibles (vu qu’il faut au moins
sont impossibles (vu qu’il faut au moins ![]() lancers pour obtenir une série de
lancers pour obtenir une série de ![]() piles consécutifs), on voit que
piles consécutifs), on voit que ![]() , ce qui entraîne que :
, ce qui entraîne que :
![Rendered by QuickLaTeX.com \[E(T_k \vert P_1 \cap \dots \cap P_{i-1} \cap F_i)=\sum_{j=k-i} ^{+\infty} (j+i) P([T_k=j])=\sum_{j=k} ^{+\infty} (j+i) P([T_k=j]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-252a82841fe973e48efeddb0f4711e3a_l3.png)
Par linéarité de la somme, ceci nous donne que :
![Rendered by QuickLaTeX.com \[\qquad \qquadE(T_k \vert P_1 \cap \dots \cap P_{i-1} \cap F_i)=\sum_{j=k} ^{+\infty} (j+i) P([T_k=j])=\sum_{j=k} ^{+\infty} jP([T_k=j])+i\sum_{j=k} ^{+\infty} P([T_k=j]).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-11594f34eee0584d3057ce687f823299_l3.png)
Comme la famille ![]() est un système complet d’événements, on constate que la deuxième somme de droite dans l’égalité ci-dessus vaut
est un système complet d’événements, on constate que la deuxième somme de droite dans l’égalité ci-dessus vaut ![]() . Comme on reconna\^it dans la première somme de droite l’espérance de
. Comme on reconna\^it dans la première somme de droite l’espérance de ![]() , on en déduit que :
, on en déduit que :
![]()
d/ Justifions que ![]() . Pour ce faire, supposons que l’événement
. Pour ce faire, supposons que l’événement ![]() soit réalisé. Alors les
soit réalisé. Alors les ![]() premiers lancers ont donné des piles, ce qui entraine que l’on a une série de
premiers lancers ont donné des piles, ce qui entraine que l’on a une série de ![]() piles consécutifs au cours des
piles consécutifs au cours des ![]() premiers lancers, et donc
premiers lancers, et donc ![]() . En d’autres termes, la variable aléatoire
. En d’autres termes, la variable aléatoire ![]() est constante égale à
est constante égale à ![]() , ce qui entraine que :
, ce qui entraine que :
![]()
Par conséquent, on en déduit que :
![]()
3/ a/ Montrons la relation : ![]() . D’après la formule de l’espérance totale appliquée à la variable aléatoire
. D’après la formule de l’espérance totale appliquée à la variable aléatoire ![]() et au système complet d’événements :
et au système complet d’événements :
![]()
![]()
on trouve avec les résultats des questions précédentes que :
![Rendered by QuickLaTeX.com \[\qquad \qquad\begin{array}{lll}E(T_k)&=&P(F_1)E(T_k\vert F_1)+P(P_1 \cap F_2)E(T_k\vert P_1\cap F_2)+...+P(P_1\cap \dots \cap P_{k-1} \cap F_k) \\ & & \\& & E(T_k\vert P_1\cap \dots \cap P_{k-1} \cap F_k) +P(P_1 \cap \dots \cap P_{k-1} \cap P_k)E(T_k \vert P_1 \cap \dots \cap P_{k-1} \cap P_k)\\& & \\&=&\displaystyle P(F_1)\left [E(T_k)+1\right ]+P(P_1 \cap F_2)[E(T_k)+2]+...+P(P_1\cap \dots \cap P_{k-1} \cap F_k) \\ & & \\& & [E(T_k)+k] +P(P_1 \cap \dots \cap P_{k-1} \cap P_k)k \\& & \\&=&\displaystyle E(T_k) \left [ P(F_1)+P(P_1 \cap F_2)+...+P(P_1\cap \dots \cap P_{k-1} \cap F_k)\right ]+ \\ & & \\& & \left [ P(F_1)+2P(P_1 \cap F_2)+...+kP(P_1\cap \dots \cap P_{k-1} \cap F_k)\right ]+P(P_1 \cap \dots \cap P_{k-1} \cap P_k)k.\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-99ec5754967ec43eed29e0c1d58f79a3_l3.png)
Comme les résultats des lancers sont indépendants et que l’on obtient pile avec probabilité ![]() (et donc face avec probabilité
(et donc face avec probabilité ![]() ) à chaque lancer, on obtient que :
) à chaque lancer, on obtient que :
![Rendered by QuickLaTeX.com \[\qquad \qquad\begin{array}{lll}E(T_k) &=&\displaystyle E(T_k) \left [ q+pq+...+p^{k-1}q\right ]+ \left [ q+2pq+...+kp^{k-1} q\right ]+kp^k \\& & \\&=&\displaystyle E(T_k) \sum_{j=0}^{k-1} p^{j}q+ \sum_{j=0}^{k-1}(j+1)p^{j} q+kp^k. \\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ff5895df5e8bf6c6b87c460699373ee6_l3.png)
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[\boxed{E(T_k) = \sum_{j=0}^{k-1} (j+1)p^jq + E(T_k) \sum_{j=0}^{k-1} p^j q + kp^k.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cc87e1762863dc7474eed210129a92a2_l3.png)
b/ Établissons finalement que : ![]() D’après les résultats sur les sommes de suites géométriques, on trouve que :
D’après les résultats sur les sommes de suites géométriques, on trouve que :
![Rendered by QuickLaTeX.com \[\sum_{j=0}^{k-1} p^j q=q\left [\frac{1-p^k}{1-p}\right ]=q\left [\frac{1-p^k}{q}\right ]=1-p^k.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6ee4c843dcfd1ba133515b1c4031cd89_l3.png)
De la même façon, comme ![]() , on obtient par linéarité de la somme que :
, on obtient par linéarité de la somme que :
![Rendered by QuickLaTeX.com \[\sum_{j=0}^{k-1} (j+1)p^jq =\sum_{j=0}^{k-1} (j+1)(p^j-p^{j+1})=\sum_{j=0}^{k-1} (j+1)p^j- \sum_{j=0}^{k-1} (j+1) p^{j+1}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5d6c7dad5264862c58d0cba61343ae82_l3.png)
En effectuant le changement d’indices ![]() dans la deuxième somme de droite, on voit que :
dans la deuxième somme de droite, on voit que :
![Rendered by QuickLaTeX.com \[\sum_{j=0}^{k-1} (j+1)p^jq =\sum_{j=0}^{k-1} (j+1)p^j- \sum_{i=1}^{k} i p^{i}=\sum_{j=0}^{k-1} (j+1)p^j- \sum_{j=1}^{k} j p^{j}.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1b41a1fbc8ca0d2222a6935b4e522adc_l3.png)
Dès lors, on obtient en regroupant ces sommes que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\displaystyle \sum_{j=0}^{k-1} (j+1)p^jq & = & \displaystyle \sum_{j=0}^{k-1} (j+1)p^j- \sum_{j=1}^{k} j p^{j}\\& & \\& = & \displaystyle 1.p^0 + \sum_{j=1}^{k-1} (j+1)p^j- \sum_{j=1}^{k-1} j p^{j} -kp^k\\& & \\& = & \displaystyle 1.p^0 + \sum_{j=1}^{k-1} (j+1-j)p^j-kp^k\\& & \\& = & \displaystyle p^0 + \sum_{j=1}^{k-1} p^j-kp^k\\& & \\& = & \displaystyle \sum_{j=0}^{k-1} p^j-kp^k\\& & \\& = & \displaystyle \frac{1-p^k}{1-p}-kp^k\\& & \\& = & \displaystyle \frac{1-p^k}{q}-kp^k.\\\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9d9bd0a2481252ed5a98f896800b6ae4_l3.png)
D’après la question précédente, on a la relation :
![Rendered by QuickLaTeX.com \[E(T_k) = \sum_{j=0}^{k-1} (j+1)p^jq + E(T_k) \sum_{j=0}^{k-1} p^j q + kp^k,\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0a802d94b2044dc2323e8582133063fc_l3.png)
laquelle se réécrit avec les calculs ci-dessus sous la forme :
![]()
En particulier, ceci entraîne que :
![]()
Par conséquent, on en déduit que :
![Rendered by QuickLaTeX.com \[\boxed{E(T_k) = \frac{1-p^k}{q p^k}.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e73c02fd69adc21dccf5316d6914326d_l3.png)
4/ Justifions tout d’abord que ![]() . Par définition, on sait que
. Par définition, on sait que ![]() est le rang du
est le rang du ![]() pile et
pile et ![]() le rang d’apparition du dernier pile de la première série de
le rang d’apparition du dernier pile de la première série de ![]() piles consécutifs. Dès lors, si
piles consécutifs. Dès lors, si ![]() prend la valeur
prend la valeur ![]() , on a obtenu une série de
, on a obtenu une série de ![]() piles consécutifs qui s’arrête au rang
piles consécutifs qui s’arrête au rang ![]() . En particulier, il y a au moins
. En particulier, il y a au moins ![]() piles parmi les
piles parmi les ![]() premiers lancers, et donc
premiers lancers, et donc ![]() . En particulier,
. En particulier, ![]() prend toujours une valeur inférieure ou égale à celle de
prend toujours une valeur inférieure ou égale à celle de ![]() , et donc
, et donc ![]() . Par croissance de l’espérance, il s’ensuit que :
. Par croissance de l’espérance, il s’ensuit que :
![]()
A présent, établissons que :
![]()
Comme ![]() et que
et que ![]() d’après les questions précédentes, on obtient avec l’inégalité ci-dessus que :
d’après les questions précédentes, on obtient avec l’inégalité ci-dessus que :
![]()
Comme ![]() et que
et que ![]() , on trouve que :
, on trouve que :
![Rendered by QuickLaTeX.com \[\begin{array}{lll}\displaystyle \frac{k}{p} \leq \frac{1-p^k}{q p^k} & \Longleftrightarrow & \displaystyle kq p^{k-1}\leq 1-p^k \\& & \\& \Longleftrightarrow & \displaystyle kp^{k-1}(1-p)\leq 1-p^k \\& & \\& \Longleftrightarrow & \displaystyle kp^{k-1}-kp^k\leq 1-p^k \\& & \\& \Longleftrightarrow & \displaystyle kp^{k-1}-1\leq (k-1)p^k.\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d4e8276126252170121d7c078f3b9d86_l3.png)
Comme la première inégalité est toujours vraie, il s’ensuit que la dernière l’est aussi, et donc :
![]()

