Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet EDHEC Maths ECS 2019
Revenir à tous les corrigés des annales maths BCE
Exercice 1 : Polynome annulateur et généralisation
1/ a/ On a 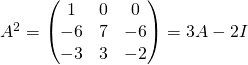 .
. ![]() est un polynôme de degré 2 annulateur de
est un polynôme de degré 2 annulateur de ![]() .
.
1/ b/ Par propriété, ![]() soit
soit ![]() .
.
Les valeurs propres possibles de ![]() sont
sont ![]() et
et ![]() .
.
1/ c/ Les valeurs propres de ![]() sont égales à celles de
sont égales à celles de ![]() .Pour
.Pour ![]() réel, on note
réel, on note ![]() . Avec le théorème du rang,
. Avec le théorème du rang, ![]() . On peut donc conjecturer que
. On peut donc conjecturer que ![]() et 2 sont effectivement valeurs propres de
et 2 sont effectivement valeurs propres de ![]() et que
et que ![]() et
et ![]() .
.
1/ d/ 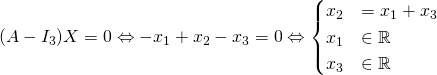 et l’espace propre associé à la valeur propre 1 est
et l’espace propre associé à la valeur propre 1 est 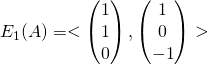 . Ces deux vecteurs ne sont pas colinéaires et forment une famille libre.
. Ces deux vecteurs ne sont pas colinéaires et forment une famille libre.![]() et
et ![]() est une base de
est une base de ![]() .
.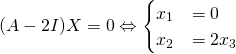 et
et 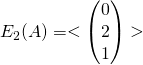 .
.
2 est valeur propre de ![]() et
et ![]() est une base de
est une base de ![]() .
.
2/ a/ Par la question 1., les valeurs propres de ![]() sont 1 et 2, et la somme des dimensions des espaces propres de
sont 1 et 2, et la somme des dimensions des espaces propres de ![]() vaut 3, soit
vaut 3, soit ![]() .
. ![]() est donc diagonalisable et
est donc diagonalisable et ![]() . La concaténation de bases de chacun des espaces propres est une base de
. La concaténation de bases de chacun des espaces propres est une base de ![]() .
.
Pour respecter les conditions imposées, changeons la base trouvée pour ![]() .
.
![Rendered by QuickLaTeX.com \[\vect<\begin{pmatrix}1\\1\\0\end{pmatrix},\begin{pmatrix}1\\0\\-1\end{pmatrix}>=\vect<\begin{pmatrix}1\\1\\0\end{pmatrix},\begin{pmatrix}1\\1\\0\end{pmatrix}-\begin{pmatrix}1\\0\\-1\end{pmatrix}>=\vect<\begin{pmatrix}1\\1\\0\end{pmatrix},\begin{pmatrix}0\\1\\1\end{pmatrix}>\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a6720fa710704123c33bf1693805593e_l3.png)
et la famille en jeu est encore libre. Prenons donc :
![]()
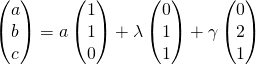 ssi
ssi 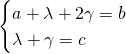 .
.
2/ b/ On trouve en résolvant ce système :
![Rendered by QuickLaTeX.com \[\begin{pmatrix}a\\b\\c\end{pmatrix}=a\begin{pmatrix}1\\1\\0\end{pmatrix}+(a-b+2c)\begin{pmatrix}0\\1\\1\end{pmatrix}+(-a+b-c) \begin{pmatrix}0\\2\\1\end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8bb1b7c5beb00500425c300634c078f5_l3.png)
3/ a/ Posons ![]() . On cherche à calculer
. On cherche à calculer ![]() .
.
Comme ![]() est une matrice diagonale, de coefficients diagonaux
est une matrice diagonale, de coefficients diagonaux ![]() , on a pour tout
, on a pour tout ![]() ,
, 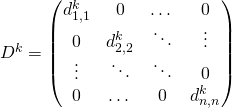 , et par règles de calcul matriciel, pour
, et par règles de calcul matriciel, pour ![]() réels :
réels :
![Rendered by QuickLaTeX.com \[a_0I+a_1D+\dots + a_pD^p=\begin{pmatrix}\sum\limits_{k=0}^pa_kd_{1,1}^k&0&\dots& 0\\0&\sum\limits_{k=0}^pa_kd_{2,2}^k&\ddots & \vdots\\\vdots & \ddots &\ddots & 0\\0&\dots & 0&\sum\limits_{k=0}^pa_kd_{n,n}^k\end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b92503b45798e1986dc7e425ad61a597_l3.png)
Il s’ensuit que
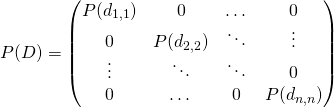 .
.
La matrice diagonale ![]() est une matrice qui comporte sur sa diagonale les valeurs propres de
est une matrice qui comporte sur sa diagonale les valeurs propres de ![]() : pour tout
: pour tout ![]() ,
, ![]() , donc tous les coefficients diagonaux de
, donc tous les coefficients diagonaux de ![]() sont des racines de
sont des racines de ![]() .
.
Finalement, ![]() .
.![]()
3/ b/ Le polynôme ![]() présenté en question précédente est donc annulateur de
présenté en question précédente est donc annulateur de ![]() et :
et :
![]()
4/a/ Pour ![]() fixé dans
fixé dans ![]() , les racines de
, les racines de ![]() sont
sont ![]() (on les a facilement car
(on les a facilement car ![]() est sous forme factorisée). Pour
est sous forme factorisée). Pour ![]() ,
, ![]() ,
, ![]() . Par produit de termes valant 1,
. Par produit de termes valant 1, ![]() .
.
![Rendered by QuickLaTeX.com \[\hbox{$L_k(\lambda_i)=\begin{cases}1&\text{ si }i=k\\0&\text{ si }i\neq k\end{cases}$\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3f83d8da25394e15ba247d791f985183_l3.png)
4/ b/
On a
Les réels sont tous nuls et la famille
Par ces trois points,
4/ c/ Soit
On a
4/ d/ On applique la question précédente au polynôme constant égal à 1, qui appartient à
5/ a/ Soit ![]() .
.
![]()
![]()
![]()
Donc pour tout
5/ b/ Par 4.d. en l’endomorphisme ![]() ,
, ![]() .
.
Soit ![]() . On applique l’endomorphisme précédent en
. On applique l’endomorphisme précédent en ![]() :
:
![Rendered by QuickLaTeX.com \[x=\id (x)=\sum\limits_{i=1}^p L_i(f)(x)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ab956d0c93cf0813741a12bed1b6c373_l3.png)
Par la question précédente, pour tout
6/ Ici ![]() , il y a deux polynômes :
, il y a deux polynômes : ![]() et
et ![]() . Soit
. Soit ![]() . Par 5.,
. Par 5.,
![]()
Comme
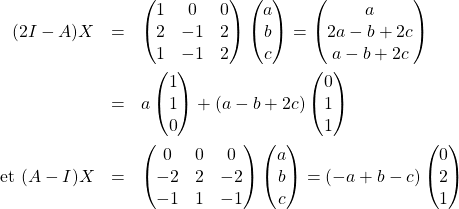
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Convergence suite de variables aléatoires
1/ a/ Pour tout réel ![]() ,
, ![]() .
.
1/ b/ ![]() .
.
Soit ![]() .
. ![]() est dérivable sur
est dérivable sur ![]() et
et
pour ![]() ,
, ![]() . Donc
. Donc ![]() est constante sur
est constante sur ![]() , égale à
, égale à ![]() .
.![]() ,
, ![]()
1/ c/ ![]() est de classe
est de classe ![]() sur
sur ![]() . Elle admet donc un développement limité à l’ordre 1 en 0 :
. Elle admet donc un développement limité à l’ordre 1 en 0 :
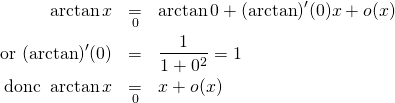
D’où :
2/ a/ ![]() est continue et positive sur
est continue et positive sur ![]() .
.
Soit ![]() .
. ![]() quand
quand ![]() . Donc l’intégrale
. Donc l’intégrale ![]() converge et vaut
converge et vaut ![]() . Par parité de l’intégrande,
. Par parité de l’intégrande, ![]() converge et vaut 1.
converge et vaut 1.![]() est une densité de probabilité.
est une densité de probabilité.
2/ b/ Soit ![]() réel.
réel.
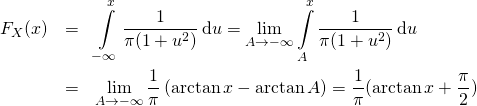
Pour
3/ a/ ![]() La fonction
La fonction ![]() est positive sur
est positive sur ![]() .
.![]() La fonction
La fonction ![]() est constante sur
est constante sur ![]() donc y est continue.
donc y est continue.
La fonction ![]() est continue sur
est continue sur ![]() et à valeurs dans
et à valeurs dans ![]() , où exp est continue. Donc
, où exp est continue. Donc ![]() est continue sur
est continue sur ![]() . Par produit avec
. Par produit avec ![]() continue sur
continue sur ![]() ,
, ![]() est continue sur cet intervalle.
est continue sur cet intervalle.![]() est donc continue sur
est donc continue sur ![]() sauf éventuellement en 0.
sauf éventuellement en 0.![]() L’intégrale
L’intégrale ![]() converge et vaut 0.
converge et vaut 0.
Soit ![]() .
.
![Rendered by QuickLaTeX.com \[\int\limits_A^1g(x)\,\mathrm{d}x=\left[e^{-1/x}\right]_A^1=e^{-1}-e^{-1/A}\underset{A\to 0^+}{\longrightarrow}e^{-1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4c7cebbad8ea6d20582ed7d067b8a1e3_l3.png)
Donc l’intégrale
Soit
![Rendered by QuickLaTeX.com \[\int\limits_1^Ag(x)\,\mathrm{d}x=\left[e^{-1/x}\right]_1^A=-e^{-1}+e^{-1/A}\underset{A\to +\infty}{\longrightarrow}1-e^{-1}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-535fbdd387d3fd536b42f2c0aab5aed9_l3.png)
Donc l’intégrale
Finalement, l’intégrale
Par ces trois points,
3/ b/ ![]() donc pour
donc pour ![]() ,
, ![]() . Soit
. Soit ![]() .
.

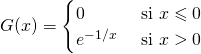
4/ a/ ![]() . Pour
. Pour ![]() réel,
réel, ![]() est réalisé ssi toutes les variables aléatoires
est réalisé ssi toutes les variables aléatoires ![]() ,
, ![]() , prennent une valeur inférieure ou égale à
, prennent une valeur inférieure ou égale à ![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*}P(M_n\leqslant x)&=&P\left( \bigcap\limits_{k=1}^n[X_k\leqslant x]\right)\\&=&\prod\limits_{k=1}^n P(X_k\leqslant x)\text{ par ind\'ependance de }X_1,\dots, X_n\\&=&[F_{X_1}(x)]^n \text{ car tous les $X_i$ suivent la m\^eme loi}\\&=&\left(\dfrac {1}{\pi}\arctan x+\dfrac 12 \right)^n\text{ par 2.b.}\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-dab8cf781274895182c84e23fcb5541d_l3.png)
Pour
4/ b/ ![]() et pour
et pour ![]() réel,
réel, ![]() .
.
Pour ![]() ,
, ![]() .
.
5/ a/ Soit ![]() .
. ![]() , donc
, donc ![]() puis
puis ![]() .
.
Comme ![]() , on a
, on a ![]() par le théorème d’encadrement.
par le théorème d’encadrement.
![]()
5/ b/ Soit ![]() . Par 1.b.
. Par 1.b. ![]() . Il s’ensuit :
. Il s’ensuit :
![]()
5/ c/ Soit ![]() .
.
![Rendered by QuickLaTeX.com \begin{eqnarray*}G_n(x)&=&\exp [n\ln \left( 1-\dfrac 1{\pi}\arctan \left( \frac{\pi}{nx}\right)\right)]\\\ln \left( 1-\dfrac 1{\pi}\arctan \left( \frac{\pi}{nx}\right)\right)&\sim& -\dfrac 1{\pi}\arctan \left( \frac{\pi}{nx}\right)\text{ d'apr\`es }\ln (1+u)\underset{0}{\sim}u\\-\dfrac 1{\pi}\arctan \left( \frac{\pi}{nx}\right)&\underset{\text{1.c.}}{\sim}&-\dfrac 1{nx}\\n\ln \left( 1-\dfrac 1{\pi}\arctan \left( \frac{\pi}{nx}\right)\right)&\sim& -\dfrac 1x\end{eqnarray*}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-afb38159ce69c6bb43900fd338da7205_l3.png)
Donc
Pour
5/ d/ En reprenant 3.b., l’ensemble des points de continuité de ![]() est
est ![]() . Par 5.a. et 5.c., pour tout
. Par 5.a. et 5.c., pour tout ![]() ,
, ![]() .
.
![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 3 : Les endomorphismes normaux
1/ a/ Par l’expression d’un vecteur dans la base orthonormée ![]() , on a :
, on a :
![Rendered by QuickLaTeX.com \[\forall x\in E,\quad x=\sum\limits_{i=1}^n \langle x, e_i\rangle e_i\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d3fcfb847c273c6105802b4786ad00cb_l3.png)
et en particulier, pour
Or
![Rendered by QuickLaTeX.com \[u^*(y)=\sum\limits_{i=1}^n \langle u(e_i),y\rangle e_i\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-102c959a33e03d9b4a1beafd9c21459d_l3.png)
1/ b/ Si ![]() existe,
existe, ![]() est parfaitement déterminé par la donnée de
est parfaitement déterminé par la donnée de ![]() , et des données de l’énoncé (
, et des données de l’énoncé (![]() et la base
et la base ![]() ).
).
Si ![]() existe,
existe, ![]() est unique.
est unique.
2/ a/ Soit ![]() .
. ![]() est une application de
est une application de ![]() dans
dans ![]() (pour
(pour ![]() ,
, ![]() est une combinaison linéaire des vecteurs de
est une combinaison linéaire des vecteurs de ![]() ).
).
Soient ![]() réel et
réel et ![]() et
et ![]() vecteurs de
vecteurs de ![]() . On a :
. On a :
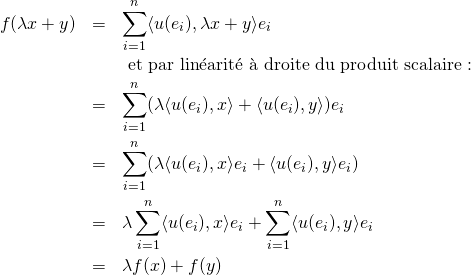
donc
L’application
2/ b/ Enfin, pour ![]() et
et ![]() dans
dans ![]() , avec la notation
, avec la notation ![]() de la question précédente, on a :
de la question précédente, on a :

Donc l’application
Par analyse-synthèse, nous avons montré l’existence et l’unicité de l’endomorphisme adjoint
![]()
3/ Quand ![]() est un endomorphisme symétrique, on a :
est un endomorphisme symétrique, on a :![]() , et par unicité de
, et par unicité de ![]() , on a
, on a ![]() .
.
De plus, ![]() dans ce cas.
dans ce cas.
Pour ![]() endomorphisme symétrique,
endomorphisme symétrique, ![]() et
et ![]() est normal.
est normal.
4/ a/ Pour ![]() ,
,
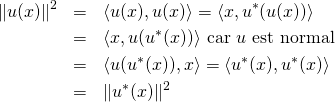
Comme les normes sont positives, ![]() .
.
4/ b/ On a :
![]()
![]() ,
,
d’où ![]()
5/ Soit ![]() un sous-espace vectoriel de
un sous-espace vectoriel de ![]() stable par
stable par ![]() . Soit
. Soit ![]() . Pour tout
. Pour tout ![]() , nous avons :
, nous avons :
![]()
Comme ![]() et que
et que ![]() est stable par
est stable par ![]() ,
, ![]() appartient à
appartient à ![]() . Et
. Et ![]() , donc
, donc ![]() .
.
Ainsi ![]() et
et ![]() .
.
Si ![]() est stable par
est stable par ![]() ,
, ![]() est stable par
est stable par ![]() .
.
6/ a/ Soit ![]() . On a
. On a ![]() . En composant par
. En composant par ![]() linéaire, on a
linéaire, on a ![]() , et comme
, et comme ![]() est normal,
est normal, ![]() . Ainsi
. Ainsi ![]() .
.
![]()
6/ b/ Soient ![]() et
et ![]() dans
dans ![]() . On a :
. On a :
![]()
soit, écrit autrement :
![]()
Par la définition d’un adjoint, on reconnaît, par unicité de l’adjoint, que
On applique 5. avec
![]()
Problème : Scilab, variable aléatoire et fonction génératrice
1/ ![]() car
car ![]() est à valeurs dans
est à valeurs dans ![]() .
.
2/ ![]() est une fonction polynomiale donc
est une fonction polynomiale donc ![]() est dérivable sur
est dérivable sur ![]() et pour
et pour ![]() réel,
réel,
![Rendered by QuickLaTeX.com \[G'(t)=\sum\limits_{k=1}^n P(X=k)kt^{k-1}\text{ et en particulier, }G'(1)=\sum\limits_{k=1}^n P(X=k)k=E(X)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-fad33b7330c8bc6c506d28376ab1de3e_l3.png)
3/ ![]() est deux fois dérivable sur
est deux fois dérivable sur ![]() comme fonction polynomiale.
comme fonction polynomiale.
Si ![]() ,
, ![]() et
et ![]() .
.
Si ![]() ,
, ![]() et pour
et pour ![]() réel :
réel :
![Rendered by QuickLaTeX.com \[G''(t)=\sum\limits_{k=2}^n k(k-1)P(X=k)t^{k-2} \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-df205a7182350d4cfe0f215f46612d9f_l3.png)
Pour tout
![]()
Nous avons donc :
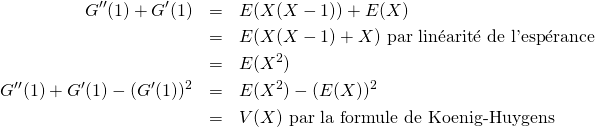
4/ a/ Soit un entier naturel ![]() non nul. Pour
non nul. Pour ![]() , on a
, on a ![]() . Par « croissance de l’intégrale » :
. Par « croissance de l’intégrale » :
![Rendered by QuickLaTeX.com \[\int\limits_k^{k+1}\frac 1{k+1}\,\mathrm{d}t\leqslant \int\limits_k^{k+1}\frac 1{t}\,\mathrm{d}t\leqslant \int\limits_k^{k+1}\frac 1{k}\,\mathrm{d}t \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9ca1323ea0135b299fd206079da27513_l3.png)
![]()
Pour tout
4/ b/ Soit ![]() ,
, ![]() . On somme les inégalités de a. pour
. On somme les inégalités de a. pour ![]() allant de 1 à
allant de 1 à ![]() :
:
![Rendered by QuickLaTeX.com \[\sum\limits_{k=1}^{n-1}\frac 1{k+1}\leqslant \sum\limits_{k=1}^{n-1}(\ln (k+1)-\ln k)\leqslant \sum\limits_{k=1}^{n-1}\frac 1k\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-08595bf030e48ad72f6ee3639718e5d8_l3.png)
et par télescopage :
Pour ![]() ,
, ![]() .
.
4/ c/ Pour ![]() ,
, ![]() , et l’encadrement précédent nous donne :
, et l’encadrement précédent nous donne :
![]()
Sans forme indéterminée, les deux suites encadrantes tendent vers 1. Par le théorème d’encadrement,
Un équivalent de
5/ ![]() est la suite des sommes partielles de la série de Riemann
est la suite des sommes partielles de la série de Riemann ![]() . Comme
. Comme ![]() , cette série converge, et donc
, cette série converge, et donc ![]() admet une limite finie.
admet une limite finie.
La suite ![]() est convergente.
est convergente.
6/ On peut compléter les lignes 6, 7 et 8 par : ![]() .
.
7/ a/ La boucle for programmée a pour effet d’attribuer à ![]() la plus grande valeur apparaissant dans
la plus grande valeur apparaissant dans ![]() . Comme
. Comme ![]() contient les entiers 1 à
contient les entiers 1 à ![]() ,
, ![]() vaut bien
vaut bien ![]() .
.
7/ b/ ![]() est la position du maximum, indice de
est la position du maximum, indice de ![]() en lequel figure la valeur
en lequel figure la valeur ![]() .
.
7/ c/ ![]()
8/ Lorsque ![]() vaut 1, la boucle
vaut 1, la boucle ![]() n’est pas exécutée, et il n’y a qu’une seule affectation concernant
n’est pas exécutée, et il n’y a qu’une seule affectation concernant ![]() , donc
, donc ![]() est la variable aléatoire certaine égale à 1.
est la variable aléatoire certaine égale à 1.
9/ a/ Le minimum du nombre d’affectations de ![]() a lieu ssi le maximum
a lieu ssi le maximum ![]() figure en première place, cas où il y a l’affectation
figure en première place, cas où il y a l’affectation ![]() et c’est tout (les tests de la boucle
et c’est tout (les tests de la boucle ![]() sont tous
sont tous ![]() ). La valeur minimale prise par
). La valeur minimale prise par ![]() est 1.
est 1.
Le maximum du nombre d’affectations de ![]() a lieu ssi le tableau est
a lieu ssi le tableau est ![]() , cas où il y a l’affectation
, cas où il y a l’affectation ![]() et une affectation par passage dans la boucle (les tests de la boucle
et une affectation par passage dans la boucle (les tests de la boucle ![]() sont tous
sont tous ![]() ). La valeur maximale prise par
). La valeur maximale prise par ![]() est
est ![]() .
.
Les situations intermédiaires sont toutes possibles ; par exemple, pour un tableau ![]() ,
, ![]() vaut 2 (il y a l’affectation initiale
vaut 2 (il y a l’affectation initiale ![]() et l’affectation lors du dernier passage en boucle
et l’affectation lors du dernier passage en boucle ![]() ).
).![]()
9/ b/ ![]() est réalisé ssi le tableau est
est réalisé ssi le tableau est ![]() , c’est-à-dire pour l’unique permutation
, c’est-à-dire pour l’unique permutation ![]() de
de ![]() , sur l’ensemble des
, sur l’ensemble des ![]() permutations équiprobables. Donc
permutations équiprobables. Donc ![]() .
.![]()
![]() est réalisé ssi le tableau débute par
est réalisé ssi le tableau débute par ![]() (soit
(soit ![]() si on utilise les notations de l’énoncé). Il y a
si on utilise les notations de l’énoncé). Il y a ![]() permutations de
permutations de ![]() débutant par
débutant par ![]() . Donc
. Donc ![]() .
.
![]() Loi de
Loi de ![]() :
: ![]() et
et ![]() .
. ![]() suit la loi uniforme sur
suit la loi uniforme sur ![]() .
.
![]() Loi de
Loi de ![]() : On a
: On a ![]() et
et ![]() et
et ![]() .
.
Ainsi ![]() , et on peut récapituler :
, et on peut récapituler :
![Rendered by QuickLaTeX.com \[\begin{center}\begin{tabular}{|l|c|c|c|c|}\hline$k$&1&2&3&4\\\hline&&&&\\$P(X_4=k)$& $\frac 14$ & $\frac {11}{24}$&$\frac 14 $& $\frac 1{24}$\\&&&&\\\hline\end{tabular}\end{center}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4018a01e9605103085760408408a56d3_l3.png)
9/ c/ Soit ![]() et
et ![]() .
.
Les événements ![]() et
et ![]() forment un système complet d’événements. Par la formule des probabilités totales :
forment un système complet d’événements. Par la formule des probabilités totales :
![]()
Intéressons-nous à
![]()
Enfin, il y a
Réfléchissons à
![]()
Enfin, ![]() . On a finalement :
. On a finalement :
![]()
9/ d/ On a vu que ![]() et
et ![]() et
et ![]() . Par c. :
. Par c. :
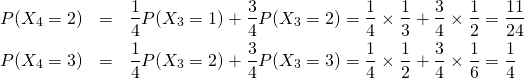
![Rendered by QuickLaTeX.com \[\begin{center}\begin{tabular}{|l|c|c|c|c|}\hline$k$&1&2&3&4\\\hline&&&&\\$P(X_4=k)$& $\frac 14$ & $\frac {11}{24}$&$\frac 14 $& $\frac 1{24}$\\&&&&\\\hline\end{tabular}\end{center}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4018a01e9605103085760408408a56d3_l3.png)
10/ a/ Pour ![]() ,
, ![]() car 0 n’est pas une valeur prise par
car 0 n’est pas une valeur prise par ![]() .
.
D’une part, ![]() par 9.b. ; d’autre part, toujours par 9.b.,
par 9.b. ; d’autre part, toujours par 9.b., ![]() , donc la relation de 9.c. est valable.
, donc la relation de 9.c. est valable.
9.c. reste valable pour ![]() .
.
10/ b/ Ainsi pour ![]() réel et
réel et ![]() ,
,
![]()
Sommons pour
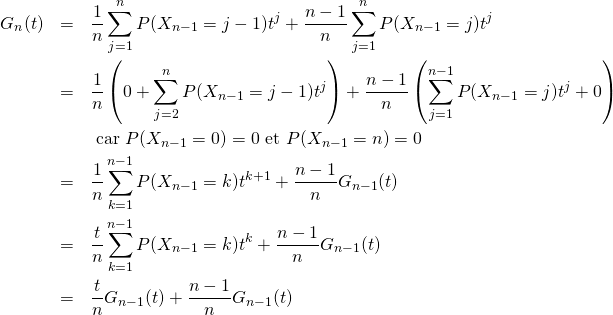
10/ c/ Soit ![]() la propriété : »
la propriété : » ![]() ,
, ![]() » qu’on montre par récurrence pour
» qu’on montre par récurrence pour ![]() .
.
Pour ![]() réel,
réel, ![]() par 8. Et
par 8. Et ![]() . Donc
. Donc ![]() est vraie.
est vraie.
Soit ![]() tel que
tel que ![]() est vraie. Soit
est vraie. Soit ![]() . Par la question précédente, appliquée avec
. Par la question précédente, appliquée avec ![]() qui est bien supérieur ou égal à 2 :
qui est bien supérieur ou égal à 2 :
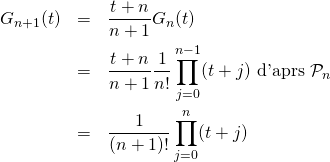
11/ La dérivation de ![]() donne :
donne :
![]()
On évalue en
![]()
Ainsi,
![Rendered by QuickLaTeX.com \[E_p-E_1=\sum\limits_{n=2}^p (E_n-E_{n-1})=\sum\limits_{n=2}^p\frac 1n=u_p-1\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-40c6e1d9808f5528b9486cb9b2946def_l3.png)
De plus, par 8.,
Pour tout
12/ a/ On dérive la relation obtenue en 11.
![]()
Avec 2., en évaluant en
![]()
et par 3. :
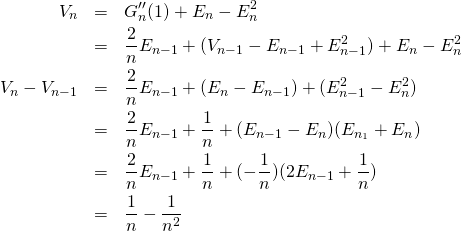
12/ b/ ![]() ,
, ![]() . Sommons ces égalités pour
. Sommons ces égalités pour ![]() allant de 2 à
allant de 2 à ![]() . Par télescopage :
. Par télescopage :
![Rendered by QuickLaTeX.com \[V_n-V_1=\sum\limits_{k=2}^n (V_k-V_{k-1})=\sum\limits_{k=2}^n (\frac 1k -\frac 1{k^2})=\sum\limits_{k=1}^n(\frac 1k -\frac 1{k^2})-0 \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5ffbfff803335c0b501ef9c0a531cc9b_l3.png)
Donc
12/ c/ Pour ![]() ,
, ![]() .
.
Comme ![]() admet une limite finie (question 5.), on a
admet une limite finie (question 5.), on a ![]() .
.
Et par 4.c., ![]() .
.
Donc ![]() .
.
On a ![]() .
.

