Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet ESSEC Maths ECS 2015
Revenir à tous les corrigés des annales maths BCE
Introduction en algèbre linéaire :
1/ a/
![]()
donc ![]()
- La fonction nulle est évidemment un élément de
 donc
donc 
Soit ![]()
![]() et
et ![]()
![]() On a
On a ![]()
![]()
![]()
![]()
= ![]()
Donc ![]()
Par suite, ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]()
1/ b/
- Soit
![Rendered by QuickLaTeX.com f\in \mathcal{C}^{0}( [ 0,1] ,\mathbb{R}) .](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20125%2020%22%3E%3C/svg%3E)
![]()
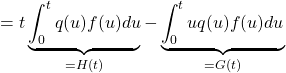
(par la linéarité de l’intégrale.)
![]() et
et
![]() sont continues sur
sont continues sur ![]()
![]() est la primitive de
est la primitive de ![]() qui s’annule en
qui s’annule en ![]() et
et ![]() celle de
celle de ![]() qui s’annule en
qui s’annule en ![]() donc
donc ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]()
Donc ![]() est de classe
est de classe ![]() sur
sur ![]() , donc continue sur
, donc continue sur ![]()
Donc ![]()
- Soit
 et
et  deux fonctions de
deux fonctions de ![Rendered by QuickLaTeX.com \mathcal{C}^{0}( [ 0,1] ,\mathbb{R})](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2087%2020%22%3E%3C/svg%3E) et
et 
![]()
![]()
![]()
![]()
![]()
+ ![]()
(par linéarité de l’intégrale)
Donc ![]()
![]()
donc
![]()
Donc ![]() est une application linéaire.
est une application linéaire.
Donc ![]() est un endomorphisme de
est un endomorphisme de ![]()
1/ c/ Soit ![]()
On a montré à la question précédente que ![]() était de classe
était de classe ![]() sur
sur ![]()
On garde alors les mêmes notations que dans la question ![]()
Donc ![]()
![]()
![]()
Donc ![Rendered by QuickLaTeX.com \boxed{\forall t\in [ 0,1] ,\,\,\,[ \Phi ( f) ] ^{\prime }( t) =\int_{0}^{t}q( u) f( u) du.}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8daf6fc79a6d45e26469a602e2ec2678_l3.png)
![]() donc
donc ![]() est de classe
est de classe ![]() sur
sur ![]() donc
donc
![]()
Et enfin, ![]() donc
donc
![]()
1/ d/ Soit ![]()
- Sens direct. Supposons que
 et que
et que 
![]() donc
donc ![]() donc d’après la question
donc d’après la question ![]()
![]()
Donc ![]()
![]() avec
avec ![]() réel.
réel.
Comme ![]() on en déduit que
on en déduit que ![]()
D’où ![]()
donc ![]()
![]() avec
avec ![]() réel.
réel.
Comme ![]() on en déduit que :
on en déduit que :
![]()
donc que ![]()
- Sens réciproque. Supposons que

Alors ![]() d’après la question
d’après la question ![]() et
et ![]()
Et d’après les expressions de ![]() et
et ![]() on a clairement :
on a clairement :
![]()
![]()
donc ![]()
Donc ![]() si et seulement si
si et seulement si ![]()
2/ a/ On pose, pour ![]() l’hypothèse de récurrence
l’hypothèse de récurrence ![]()
![]()
Au rang ![]()
![]()
et ![]()
car ![]()
Donc ![]() est vraie.
est vraie.
Soit ![]() On suppose
On suppose ![]() vraie.
vraie.
Pour ![]()
![]()
![]()
![]()
car les bornes sont en ordre croissant.
Or ![]()
![]() et
et ![]()
car pour ![]()
Et en utilisant ![]()
on a ![]()
![]()
![]()
Les bornes sont en ordre croissant, donc :
![]()
![]()
Or
![]()
donc
![]()
et ![]() est vraie.
est vraie.
Par principe de récurrence, on a montré que
![]()
2/ b/ Soit ![]() On a :
On a :
![]()
et ![]() (terme général d’une série exponentielle),
(terme général d’une série exponentielle),
donc, par le théorème d’encadrement,
![]()
Donc ![]()
2/ c/ Soit ![]() telle que
telle que ![]() Donc, d’après
Donc, d’après ![]() on a
on a ![]()
On pose alors, pour ![]() l’hypothèse de récurrence
l’hypothèse de récurrence ![]()
![]()
![]() est vraie par définition.
est vraie par définition.
Soit ![]() On suppose
On suppose ![]() vraie. Alors
vraie. Alors
![]()
Donc ![]() est vraie.
est vraie.
Donc, ![]()
Soit alors ![]() On a
On a ![]() et d’après la question
et d’après la question ![]()
![]()
Donc ![]()
Donc ![]()
2/d/ Soit ![]() et
et ![]()
![]()
Donc par linéarité de la dérivation,
![]()
![]()
![]()
Donc ![]()
Donc ![]()
Si ![]() alors
alors ![]() et
et ![]() et d’après la question
et d’après la question ![]()
![]() est nulle.
est nulle.
Comme la réciproque est claire, on a ![]() donc
donc ![]()
![]() :
:![]() est une application linéaire injective
est une application linéaire injective
donc l’application ![]() est linéaire bijective, i.e. est un isomorphisme d’espaces vectoriels,
est linéaire bijective, i.e. est un isomorphisme d’espaces vectoriels,
donc
![]()
Et enfin, donc F( q) est un espace vectoriel de dimension finie avec ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie I sur les espaces vectoriels.
3/ a/ ![]()
{ ![]()
![]()
![]() }
}
donc ![]()
La fonction nulle est clairement un élément de ![]() donc
donc ![]()
Soit ![]() et
et ![]()
![]() On a
On a ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
et de même ![]()
Donc ![]()
Donc ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]()
3/ b/ Soit ![]() Alors
Alors ![]() et
et ![]()
Donc ![]() et
et ![]()
![]() avec
avec ![]() et
et ![]() réels.
réels.
Or ![]() donc
donc ![]() et
et ![]() , donc
, donc ![]()
Donc ![]()
L’inclusion inverse étant claire, on a ![]()
4/ a/ On suppose ![]() et on note pour
et on note pour ![]()
![]() est de classe
est de classe ![]() sur
sur ![]()
Et, pour ![]()
![]() et
et ![]()
Donc ![]()
De même, ![]() est aussi dans
est aussi dans ![]()
![]()
{ ![]()
![]()
![]() }
}
![]()
Or d’après l’introduction,
![]()
De plus, en gardant les notations ci-dessus, ![]() et
et ![]() sont dans
sont dans ![]()
Et ces deux applications sont toutes deux non nulles, et elles ne sont pas colinéaires.
Donc ![]() est libre et
est libre et
![]()
On en déduit que ![]() et
et ![]()
Donc
![]()
![]()
![]()
![]()
et
![]()
Donc, d’après la résolution précédente,
![]()
4/b/ On suppose que ![]() et on note, pour
et on note, pour ![]() et
et ![]()
![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]()
Et pour ![]()
![]() et
et
![]()
Donc ![]()
De même, ![]()
Or d’après l’introduction, on a toujours
![]()
De plus, en gardant les notations ci-dessus, ![]() et
et ![]() sont dans
sont dans ![]()
Enfin, ![]() et
et ![]() sont deux applications non nulles et non colinéaires, donc la famille
sont deux applications non nulles et non colinéaires, donc la famille ![]() est libre
est libre
On en déduit que ![]() et
et ![]()
Donc ![]()
{ ![]()
![]()
![]() }
}
![]()
et ![]()
![]() avec
avec
![]()
![]()
![]() ou bien
ou bien ![]()
Alors ![]() et
et ![]()
![]()
![]()
![]() ou bien
ou bien ![]() Alors
Alors ![]() et
et ![]()
Conclusion : ![]() si
si ![]()
et ![]() si
si ![]() où
où ![]()
5/ Posons ![]()
On a donc ![]()
![]() étant une application linéaire,
étant une application linéaire, ![]() aussi.
aussi.
Soit ![]() On suppose que
On suppose que ![]() Alors
Alors ![]() donc
donc ![]() donc
donc ![]() car
car ![]() est injective.
est injective.
Donc ![]() et
et ![]() est injective.
est injective.
![]() donc d’après le théorème du rang :
donc d’après le théorème du rang :
![]()
![]()
donc ![]()
Or ![]()
![]()
car si ![]() alors
alors ![]()
Donc ![]() et
et ![]()
Donc ![]()
6/ On suppose que ![]()
D’après la question précédente, on a alors ![]() On pose alors
On pose alors ![]() où
où ![]()
![]() donc
donc ![]() est de classe
est de classe ![]()
sur ![]()
![]() et
et ![]()
![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() donc par le théorème d’intégration par parties,
donc par le théorème d’intégration par parties,
![]()
![]()
![]()
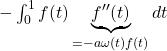
Donc
![]()
 est continue à valeurs strictement positives, et
est continue à valeurs strictement positives, et  est continue, positive et
est continue, positive et  par hypothèse,
par hypothèse,
donc ![]() est continue
est continue
positive et non identiquement nulle sur ![]()
Or les bornes sont en ordre croissant, donc ![]()
 est continue et positive sur
est continue et positive sur ![Rendered by QuickLaTeX.com [ 0,1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2032%2018%22%3E%3C/svg%3E) et les bornes sont en ordre croissant,
et les bornes sont en ordre croissant,
donc ![]()
Donc 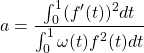
avec ![]() et
et
![]() donc
donc ![]()
Or ![]() d’après la question
d’après la question ![]() donc puisque
donc puisque ![]() on a
on a ![]()
7/ On note ![]() le temps de cette question.
le temps de cette question.
On a ![]()
![]()
- Soit
 Alors
Alors 
est continue sur![Rendered by QuickLaTeX.com [ 0,1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2032%2018%22%3E%3C/svg%3E) et
et  est bien définie.
est bien définie.
Donc ![]() est bien une
est bien une
application définie sur ![]() à valeurs dans
à valeurs dans ![]()
- Soit

![]()
![]()
![]()
Donc ![]() est symétrique.
est symétrique.
- Soit
 et
et 
Par linéarité de l’intégration :
![]()
![]()
![]()
![]()
![]()
Donc ![]() est linéaire par rapport
est linéaire par rapport
à sa première variable.
Et grâce à la symétrie, ![]() est bilinéaire.
est bilinéaire.
- Pour
 on a
on a
![]()
Or ![]() est continue positive sur
est continue positive sur ![]() et les bornes sont en ordre croissant,
et les bornes sont en ordre croissant,
donc ![]() donc
donc
![]()
D’où la positivité.
- Soit
 telle que
telle que 
![]() est continue de signe constant positif sur
est continue de signe constant positif sur ![]()
et ![]()
donc ![]()
Donc ![]() car
car
![]()
Donc ![]() est définie.
est définie.
![]() est une forme bilinéaire, symétrique, définie et positive, donc
est une forme bilinéaire, symétrique, définie et positive, donc
![]()
8/ Soit ![]()
- ou bien
 . Alors
. Alors  et
et 
- ou bien
 . Alors
. Alors  et
et 
- ou bien
 et
et 
Soit ![]() et
et ![]()
![]()
![]()
![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() donc par le théorème d’intégration par parties,
donc par le théorème d’intégration par parties,
![]()
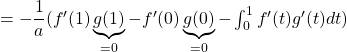
![]()
De même, en échangeant les rôles de ![]() et
et ![]() on a
on a ![]()
Donc
![]()
Donc ![]()
Comme ![]() on en déduit :
on en déduit : ![]() et
et ![]()
Donc ![]() ,
,
donc ![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie II : l’exemple ω = 1
9/ a/ Soit ![]()
 est de classe
est de classe  sur
sur ![Rendered by QuickLaTeX.com [0,1] .](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2038%2018%22%3E%3C/svg%3E)
![Rendered by QuickLaTeX.com \forall t\in [ 0,1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2072%2018%22%3E%3C/svg%3E) ,
,
![]()
![]()
Donc
![]()
Donc ![]()
et on a bien trouvé ![]() tel que
tel que ![]()
9/ b/ Soit ![]()
![]()
Or, pour ![]()
![]()
donc ![]()
![]()
donc ![]()
![]()
- ou bien
 Alors
Alors 
![]()
- ou bien
 Alors
Alors 
![]()
Donc, 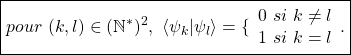
9/ c/ D’après a), ![]() est donc une famille orthonormée de
est donc une famille orthonormée de ![]()
![]() est une famille orthonormée de
est une famille orthonormée de ![]() , donc
, donc ![]() est une famille libre de
est une famille libre de ![]()
Comme, par définition, ![]() est une famille génératrice de
est une famille génératrice de ![]() on en déduit que
on en déduit que ![]() est une base de
est une base de ![]()
![]()
10/ a/ On a pour ![]()
![]()
![]()
![]()
- Soit
 et
et 
![]()
![]()
![]()
Donc par linéarité par rapport à la première variable du produit scalaire, on a :
![]()
![]()
![]()
Donc, ![]() ,
,
![]()
![]()
![]()
Donc ![]()
Donc ![]() est une application linéaire définie sur
est une application linéaire définie sur ![]()
- Soit
![Rendered by QuickLaTeX.com k\in [ \![ 1,p] \!] .](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2075%2018%22%3E%3C/svg%3E)
![]()
![]()
Or ![]()
ou bien ![]()
Alors, ![]()
![]()
Or, pour ![]()
![]()
donc ![]()
Donc ![]()
![]()
![]()
Donc ![]()
ou bien ![]()
Alors ![]()
![]()
Donc,
![]()
![]()
D’où : 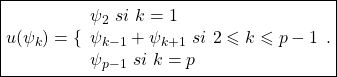
et ![]()
Soit alors ![]() Comme
Comme ![]() est une base de
est une base de ![]()
![]()
Par linéarité de ![]() on a donc
on a donc
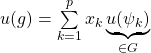 et
et ![]()
Donc ![]()
![]() est une application linéaire sur
est une application linéaire sur ![]() et
et ![]() donc
donc
![]()
10/ b/ On note ![]()
D’après les calculs effectués à la question précédente, on trouve ![]()

![]() est une matrice symétrique réelle, donc
est une matrice symétrique réelle, donc ![]()
11/ a/ Soit ![]()
![]()
![]()
donc par linéarité de l’intégrale, ![]()
![]()
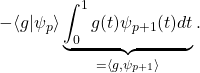
Or ![]() et
et ![]()
donc ![]()
Donc 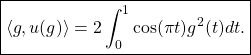
11/ b/ Soit ![]() une valeur propre de
une valeur propre de ![]() et
et ![]() un vecteur propre associé.
un vecteur propre associé.
donc ![]()
donc ![]()
Or ![]() est un vecteur propre, donc
est un vecteur propre, donc ![]() et
et ![]()
Donc 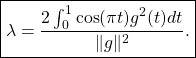
![]() et
et ![]() donc
donc ![]()
![]()
Les bornes étant en ordre croissant, on en déduit :
![]()
Donc,
![]()
et comme ![]()
Donc ![]()
- Supposons que

D’après le point précédent, on en déduit que
![]()
Or ![]() donc
donc
![]()
De plus, ![]() est {continue} et de signe constant positif sur
est {continue} et de signe constant positif sur ![]()
donc, par le caractère défini de l’intégrale, ![]()
Or ![]()
donc ![]()
donc ![]()
Comme ![]() est continue sur
est continue sur ![]()
![]()
Donc ![]()
![]()
On obtient une contradiction avec ![]() vecteur propre, donc
vecteur propre, donc ![]()
- On prouve de même que

12/ a/ On rappelle qu’on a noté ![]()
On note 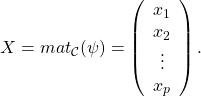
![]()

=
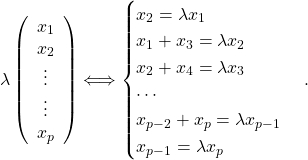
Donc 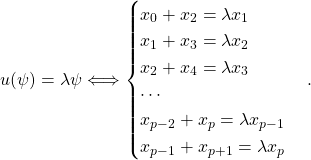
puisque ![]()
Donc ![]()
![]()
Donc ![]()
12/ b/ Soit ![]() définie par :
définie par :
![]() et
et ![]()
Donc ![]() est une suite récurrente linéaire double d’équation caractéristique
est une suite récurrente linéaire double d’équation caractéristique
![]()
![]() donc les solutions de
donc les solutions de ![]() sont
sont ![]() et
et ![]()
Et d’après le cours, il existe
![]()
![]()
donc il existe
![]()
![]() =
= ![]()
12/ c/ ![]() , donc
, donc ![]()
![]() donc
donc ![]()
Or ![]() car sinon
car sinon
![]() donc
donc ![]()
et on a une contradiction avec ![]() vecteur
vecteur
propre de ![]()
Donc on obtient ![]()
Or, ![]()
![]()
![]()
De plus, ![]()
![]()
![]()
Donc ![]()
12/ d/ On a montré dans les questions précédentes, que si ![]() est valeur propre de
est valeur propre de ![]()
alors ![]()
et alors en notant ![]() la matrice représentative dans
la matrice représentative dans ![]() d’un vecteur propre, on a
d’un vecteur propre, on a
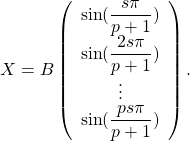
Réciproquement, prenons ![]()
On pose 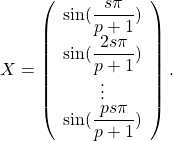
Alors 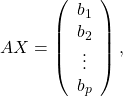 avec
avec
![]()
![]()
car pour ![]()
![]() et
et
pour ![]()
![]()
Donc, ![]()
![]()
![]()
+
![]()
![]()
Donc ![]()
donc ![]()
Comme ![]() on a
on a ![]() est une valeur propre de
est une valeur propre de ![]() et
et ![]() est un vecteur propre associé.
est un vecteur propre associé.
En rassemblant tous les résultats, on a donc montré que ![]()
![]()
et que pour ![]() le sous-espace propre associé à
le sous-espace propre associé à ![]() noté
noté ![]() est
est ![]() , où
, où
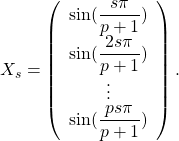
Donc ![]() forme une base de vecteurs propres de
forme une base de vecteurs propres de ![]()
13/ Lorsque ![]() , nous avons vu que
, nous avons vu que
![]()
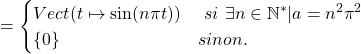
c’est-à-dire que les seuls réels ![]() pour lesquels
pour lesquels ![]() sont ceux qui s’écrivent
sont ceux qui s’écrivent ![]() pour
pour ![]() .
.
Par l’absurde, si ![]() était vérifiée, il existerait une suite
était vérifiée, il existerait une suite ![]() de réels deux à deux distincts tels que
de réels deux à deux distincts tels que ![]() ,
, ![]() .
.
Cette suite serait alors constituée d’une infinité de réels de la forme ![]() avec
avec ![]() , on aurait donc que
, on aurait donc que ![]() . La suite ne pourrait donc pas être bornée, ce qui contredit
. La suite ne pourrait donc pas être bornée, ce qui contredit ![]() .
.
On conclut que ![]() n’est pas vérifiée lorsque
n’est pas vérifiée lorsque ![]() .
.
14/ D’après ![]() ,
, ![]() ,
,![]() ,
,
donc ![]() tel que
tel que ![]() .
.
Le produit scalaire étant défini positif,
![]()
Donc ![]() vérifie
vérifie
![]() .
.
De plus,
![]()
car ![]() , espace vectoriel, est stable par multiplication par un réel.
, espace vectoriel, est stable par multiplication par un réel.
Donc ![]() convient.
convient.
On a montré : ![]()
![]()
15/ a/
- Remarquons que
 est une famille orthonormée :
est une famille orthonormée :
En effet, ![]() ,
,
donc ![]() .
.
De plus,![]() ,
, ![]() , donc d’après la question 8,
, donc d’après la question 8,
![]() , donc
, donc ![]() .
.
- Pour
 ,
, 
Donc, ![]() étant une base orthonormée de
étant une base orthonormée de ![]() , d’après l’expression du projeté orthogonal en fonction d’une base orthonormée de l’espace sur lequel on projette, comme
, d’après l’expression du projeté orthogonal en fonction d’une base orthonormée de l’espace sur lequel on projette, comme
![]()
![]() est le projeté orthogonal de
est le projeté orthogonal de ![]() sur
sur ![]() .
.
15/ b/ D’après l’expression de la norme dans une base orthonormée ,
![]() .
.
De plus, ![]() étant le projeté orthogonal de
étant le projeté orthogonal de ![]() sur
sur ![]() ,
,
il existe ![]() tel que
tel que
![]()
D’après Pythagore,
![]() ,
,
donc ![]()
15/ c/ La série ![]() est à termes positifs et ses sommes partielles sont majorées par
est à termes positifs et ses sommes partielles sont majorées par ![]() , cette série converge donc.
, cette série converge donc.
15/ d/
- Le terme général d’une série convergente a une limite nulle,
d’où ![]() ,
,
d’où ![]() .
.
 , donc
, donc  comme
comme  et que
et que  est à valeurs strictement positives
est à valeurs strictement positives  ,
,
donc ![]()
Donc ![]()
16/ a/ Soit ![]() et
et
![Rendered by QuickLaTeX.com \varphi _x: t\in [0,1]\mapsto \begin{cases} t(x - 1)&{ si~ } t\in [0,x]\\ x(t - 1)&{ si~ } t\in ]x,1] \end{cases}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-461fdb227b814b376a3cffcdb0a24ff7_l3.png)
![]() est affine sur chacun des intervalles
est affine sur chacun des intervalles ![]() et
et ![]() , donc continue (i.e. de classe
, donc continue (i.e. de classe ![]() ) sur
) sur ![]() .
.
De plus, ![]()
![]()
![]()
et ![]()
![]()
![]() .
.
Donc ![]() est continue sur
est continue sur ![]() .
.
16/ b/ ![]() est de classe
est de classe ![]() sur
sur ![]() , donc d’après la formule de Taylor-reste intégral à l’ordre
, donc d’après la formule de Taylor-reste intégral à l’ordre ![]() sur
sur ![]() , où
, où ![]() , on a :
, on a :
![]()
![]()
Donc ![]()
![]()
En particulier, pour ![]() , il vient :
, il vient :
![]() .
.
Comme ![]() car
car ![]() , on en déduit :
, on en déduit :
![]()
16/ c/
- D’après
 et
et  , pour tout
, pour tout ![Rendered by QuickLaTeX.com x\in [0,1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2065%2018%22%3E%3C/svg%3E) ,
,
![]()
![]()
D’après la relation de Chasles et la linéarité de l’intégrale,
![]()
![]()
![]()
Donc
![]()
![]()
D’où ![]()
![]()
Ceci s’écrit encore: ![]()
![]()
D’où ![]()
- D’après la question 16a,
 est continue sur
est continue sur ![Rendered by QuickLaTeX.com [0,1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2032%2018%22%3E%3C/svg%3E) , donc d’après la question 15d,
, donc d’après la question 15d, 
d’où ![]()
16/ d/
 , donc
, donc  , donc d’après la question 16c,
, donc d’après la question 16c,
![]()
![]()
- D’après l’inégalité de Cauchy-Schwarz,
![]()
![]()
![]()
![]() , donc
, donc ![]() .
.
16/ e/
- Calculons
 :
:
![]()
![]()
![]()
![]()
![]()
D’où ![]()
![]()
Donc en passant aux racines carrées,
![]()
D’où ![]()
D’après la question 16d,
![]()
16/ f/ Par définition du nombre dérivé,
![]()
![]()
![]()
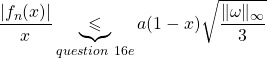
![]()
Par passage à la limite quand ![]() tend vers
tend vers ![]() il vient :
il vient : ![]()
16/ g/
 est continue sur
est continue sur ![Rendered by QuickLaTeX.com [0,1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2032%2018%22%3E%3C/svg%3E) , donc sur
, donc sur ![Rendered by QuickLaTeX.com [0,x]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2033%2018%22%3E%3C/svg%3E) , donc
, donc
![]() .
.
Mais ![]() , donc
, donc
![]() .
.
- Par inégalité triangulaire,
![]() (#)
(#)
- Majorons
 :
:
![]()
![]()
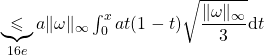
![]()
Or ![]() car
car
![]()
Par positivité de l’intégrale,
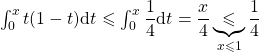
D’où
![]()
- En majorant
 à l’aide de la question 16f, (#) entraîne:
à l’aide de la question 16f, (#) entraîne:
![]()
D’où 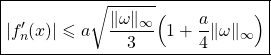
17/ ![]() est de classe
est de classe ![]() , donc en particulier dérivable sur
, donc en particulier dérivable sur ![]() , donc sur
, donc sur ![]() pour tout
pour tout ![]() .
.
De plus,
![]() .
.
D’après le théorème des accroissements finis,
![]()
![]()
18/ Soit ![]()
18/ a/ D’après la question 16c, Pour tout ![]() ,
, ![]() ,
,
donc pour tout ![]() ,
, ![]() .
.
Ceci se traduit par: ![]()
Notons ![]() , on a alors:
, on a alors:
![]() .
.
On a montré: ![]()
18/ b/
- Soit
 et
et  .
.
Par définition de la partie entière, ![]()
et ![]() ,
,
donc ![]() ,
,
donc ![]() .
.
D’après l’inégalité triangulaire, ![]()
![]()
Or d’après la question 17,
![]()
![]()
![]()
De plus, ![]() , donc d’après la question 18a,
, donc d’après la question 18a, ![]() .
.
On majore alors ![]() grâce à
grâce à ![]() :
:
![]() .
.
- Si
 , alors
, alors 
On a montré : ![]()
18/ c/ Ceci s’écrit encore: ![]()
ce qui traduit ![]() .
.
18/ d/ On a :
![]()
D’après la question 18c,
![]() ,
,
donc par encadrement, ![]()
![]()
![]() .
.
Mais nous avons raisonné par l’absurde en supposant, juste avant la question 14, que l’hypothèse (![]() ) était réalisée ;
) était réalisée ;
ceci impliquait, dans la question 14, l’existence de ![]() telle que
telle que ![]() ,
,
donc ![]() .
.
Le résultat ![]() est donc en contradiction avec la question 14, donc avec l’hypothèse (
est donc en contradiction avec la question 14, donc avec l’hypothèse (![]() ), qui est donc fausse.
), qui est donc fausse.
Nous concluons que l’hypothèse (![]() ) n’est jamais réalisée.
) n’est jamais réalisée.

