Mon parcours pour réussir en maths

Je révise en autonomie

Je progresse avec un prof

Je m’entraîne sur des annales corrigées

Avis Google France
★★★★★ 4,9 sur 5

Corrigé maths ESSEC ECS 2018

Revenir à tous les corrigés des annales de maths BCE

Partie 1 : Convergence de suite

1. Soient $x \in [-r,r]$ et $k \in \mathbb{N}$ . Pour tout $n \in \mathbb{N}$ , $0\leqslant n^k$ $|a_n|$ $|x|^n \leqslant n^k$ $|a_n|$ $r^n$ . Ceci implique la convergence de la série $\sum_n n^k$ $|a_n|$ $|x|^n$ par comparaison à la série numérique $\sum_n n^k$ $|a_n|r^n$ , convergente ( $(a_n)_n \in A(r)$ ).

Pour $0 < x = r'\leqslant r$ , le résultat au dessus montre que $(a_n)_n \in A(r')$ . Tout ceci justifie l’inclusion $A(r) \subset A(r')$ .

2. Soient deux réels r et r’ tels que $0 < r' \leqslant r$ . Soit une suite $(a_n)_n$ , l’inégalité de la question 1. écrite pour $k = 0$ et $x = r' \in [-r, r]$ met en évidence que la convergence de $(a_n r^n)_n$ vers 0 entraîne par encadrement celle de $(a_n r'^n)_n$ vers 0, ce qui justifie la première inclusion $B(r)\subset B(r')$ .

Enfin, puisque la convergence de la série $\sum_n n^k |a_n| r^n$ pour k = 0 entraîne la convergence de son terme général vers 0, on a l’inclusion $A(r) \subset B(r)$ .

3. Soit $r > 0$ . La suite nulle appartient de manière évidente à A(r). Soient deux suites $(a_n)_n$ , $(b_n)_n \in A(r)$ et un réel $\lambda$ , on a pour $k \in \mathbb{N}$ :

$\forall_n \in \mathbb{N}, 0\leqslant n^k |\lambda a_n+b_n|r^n$

$\leqslant |\lambda| n^k |a_n|r^n+ n^k |b_n| r^n,$

de sorte que la série $\sum_n n^k |\lambda a_n + b_n| r^n$ converge par comparaison aux séries convergentes $\sum_n n^k |a_n| r^n$ et $\sum_n |b_n| r^n$ : la suite $\lambda(a_n)_n + (b_n)_n$ appartient donc à A(r). Ainsi A(r) est-il un sous-espace vectoriel de $\mathbb{R}^\mathbb{N}$ .

4.a. Pour $k \in \mathbb{N}$ , on a $\forall_n \in \mathbb{N}, \dfrac{u_{n+1}(k)}{u_n(k)}= (1+\dfrac{1}{n})^{k+2} \dfrac{r}{n+1} \overrightarrow{n \longrightarrow \infty} 0<1,$ si bien qu’il existe un rang $n_0$ (dépendant de k) tel que pour tout $n \geq n_0$ , $\dfrac{u_{n+1}(k)}{u_n(k)} \leq \dfrac{1}{2}$ puis, par récurrence immédiate :

$\forall n \geq n_0, 0\leq u_n(k) \leq \dfrac{u_{n0}(k)}{2^{n-n_0}}$

d’où l’on déduit par encadrement que $u_n(k) = n^2 n^k \alpha_n r^n$ tend vers 0 lorsque $n \longrightarrow \infty$ . Il en ressort que $0 \leq n^k |\alpha_n| r^n = \circ(\dfrac{1}{n^2})$ lorsque $n \longrightarrow \infty$ , et donc que la série $\sum_n n^k |\alpha_n| r^n$ converge par comparaison à la série de Riemann convergente $\sum_{n\geq 1} \dfrac{1}{n^2}$ . La suite $\alpha$ appartient donc à A(r).

b. Soient deux réels $\lambda$ , $r > 0$ , la suite $\beta(\lambda)$ appartient à B(r) si, et seulement si, la suite géométrique $(\lambda^n r^n)_n$ converge vers 0 c’est-à-dire si, et seulement si, $|\lambda_r|< 1$ ou encore $0 < r < \dfrac{1}{\lambda}$ .

Lorsque $0 < r < \dfrac{1}{\lambda}$ , la suite $(n^{k+2} \lambda^n r^n)_n$ converge vers 0 pour tout $k \in \mathbb{N}$ par croissances comparées, et l’on en déduit comme en a. que la série $\sum_n n^{k} \lambda^n r^n$ converge : la suite numérique $\beta(\lambda)$ appartient alors à A(r).

Pour $r \geq \dfrac{1}{\lambda}$ en revanche, la série $\sum_n \lambda^n r^n$ est grossièrement divergente et la suite $\beta(\lambda)$ n’appartient pas à A(r). En conclusion, la suite $\beta(\lambda)$ appartient à A(r) si, et seulement si, $0 < r < \dfrac{1}{\lambda}$ .

5. Soit $r \in ]0, \varrho[$ . Pour $k \in \mathbb{N}$ ,

$0\leq n^k |a_n|r^n$

= $|a_n| \varrho^n. n^k (\dfrac{r}{\varrho})^n$

= $\circ(n^k(\dfrac{r}{\varrho})^n), n\longrightarrow \infty$

car le facteur $|a_n|$ $\varrho^n$ tend vers 0 lorsque $n\longrightarrow \infty$ , d’où l’on déduit la convergence de la série $\sum_n n^k |a_n|r^n$ par comparaison à la série $\sum_n n^k (\dfrac{r}{\varrho})^n$ , convergente d’après 4.b. puisque $0 < r <\varrho$ : la suite $(a_n)_n$ appartient donc à A(r).

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Partie 2 : convergence de série

6. La série $\sum_n a_n x^n$ est convergente pour x = 0. Pour $x \in ]-R, R[ \setminus {0},$ elle est absolument convergente d’après la question 5. appliquée à $r = |x| < R$ sachant que $(a_n) \in B(R)$ par hypothèse.

7.a. On applique sur $[x, x+h] \subset [-r, r]$ l’inégalité des accroissements finis à la fonction $\varphi_n: t\longrightarrow t^n$ , de classe $\ell^1$ sur [-r, r] telle que $|\varphi'_n(t)| = n |t|^{n-1} \leq nr^{n-1}$ pour tout $t \in [-r, r]$ , on obtient

$|(x + h)^n - x^n|$

= $|\varphi_n(x + h) -\varphi_n(x)| \leq nr^{n-1} |h|$ .

b. D’après a., pour $x \in [-r, r]$ et h tel que $x + h \in [-r, r]$ ,

$|f_a(x + h)- f_a(x)|$

$=|\sum_{n=0}^{\infty} a_n((x + h)^n - x^n)|$

$\leqslant \sum_{n=0}^{\infty} |a_n| |((x + h)^n - x^n)|$

$\leqslant \sum_{n=0}^{\infty} |a_n| n r^{n-1}|h|$

$=\dfrac{|h|}{r}\sum_{n=0}^{\infty} n|a_n|r^n,$

toutes séries convergentes d’après la question 5..

c. De l’inégalité établie à la question 7.b., on déduit par encadrement que $f_a(x + h) \longrightarrow f_a(x)$ lorsque $h \longrightarrow 0$ sous la contrainte $x + h \in [-r, r]$ . Ainsi la restriction à [-r, r] de $f_a$ est-elle continue $^ 1$ .

Soit un réel $x \in ]-R, R[$ , il existe alors $r \in ]0, R[$ tel que $x \in ]-r, r[$ . Comme la continuité est une notion locale, la continuité de la restriction $f_a|_[-r,r]$ au point intérieur x donne celle de la fonction $f_a$ au même point, et l’on justifie ainsi que $f_a$ est continue sur ]-R, R[.

8.a. Sachant que $(a_n) \in B(R)$ et que $0 < \varrho < R$ , la question 5. assure que $(a_n) \in A(\varrho)$ . Il en résulte en particulier que la série $\sum_n |a_n| \varrho^n$ converge et par conséquent que la suite $(n |a_n| \varrho^n)$ converge vers 0 : la suite $(n a_n)_n$ appartient donc à $B(\varrho)$ . D’après la remarque suivant la question 3., on peut alors appliquer les questions 6. et 7. à la suite $((n + 1)a_{n+1})_n$ , qui garantissent que la fonction

$x\longrightarrow \sum_{n=0}^{\infty} (n+1)a_{n+1}x^n$

$= \sum_{n=0}^{\infty} n a_n x^{n-1}=g_a(x)$

est bien définie et continue sur $]-\varrho, \varrho[$ . Puisque le réel $\varrho$ est un élément quelconque de l’intervalle [r, R[, il en ressort par un raisonnement analogue à celui mené en 7.c. que $g_a$ est bien définie et continue sur ]-R, R[.

b. Il s’agit d’une application directe du théorème fondamental à la fonction $S_n$ , polynomiale donc de classe $C^1$ sur $\mathhbb{R}$ : pour $n \in \mathbb{N}^\ast$ ,

$S_n(x) = S_n(0) + \int^{x}_{0}S'_n(t)dt$

$=a_0+\int^{x}_{0}S'_n(t)dt$

c. Pour $n \in \mathbb{N}^\ast$ et $x \in [0, r]$ ,

$|\int^{x}_{0}g_a(t)-S'_n(t)dt|$

$=|\int^{x}_{0}(\sum_{k=n+1}^{\infty}ka_kt^{k-1})dt|$

$\leq\int^{x}_{0}|\sum_{k=n+1}^{\infty}ka_kt^{k-1}|dt$

$\leq \int^{x}_{0}(\sum_{k=n+1}^{\infty}k|a_k| t^{k-1})dt$

$\leq \int^{x}_{0}(\sum_{k=n+1}^{\infty}k|a_k| r^{k-1})dt$

$= x \sum_{k=n+1}^{\infty}k|a_k| r^{k-1}$

$\leq \sum_{k=n+1}^{\infty}k|a_k| r^k$

Pour $x \in [-r, 0]$ , on procède de même après avoir pris soin de réordonner les bornes d’intégration par ordre croissant (derrière les valeurs absolues), afin de pouvoir utiliser l’inégalité triangulaire et la croissance de l’intégrale :

$|\int^{x}_{0}(g_a(t)-S'_n(t)dt|$

$\leq\int^{x}_{0}(\sum_{k=n+1}^{\infty}k|a_k| r^{k-1})dt$

$=|x| \sum_{k=n+1}^{\infty}k|a_k| r^{k-1}$

$\leq \sum_{k=n+1}^{\infty}k|a_k| r^k$

d. D’après la question 8.c.

$\forall n \in \mathbb{N}^\ast, |\int^{x}_{0}(g_a(t)-\int^{x}_{0} S'_n(t)dt|$

$\leq \sum_{k=n+1}^{\infty}k|a_k| r^k,$

où le membre de droite converge vers 0 lorsque $n \longrightarrow \infty$ comme reste d’une série convergente. Par encadrement, on en déduit que :

$\int^{x}_{0}(g_a(t)$

$= \lim_{n\longrightarrow\infty}\int^{x}_{0}S'_n(t)dt$

$=\lim_{n\longrightarrow\infty} \sum_{k=1}^{n}\int^{x}_{0}ka_k t^{k-1}dt$

$=\lim_{n\longrightarrow \infty} \sum_{k=1}^{n} a_k x^{k}=f_a(x)-a_0,$

e. Puisque la fonction $g_a$ est continue sur ]-R, R[ d’après a., la fonction $x \longrightarrow \int^{x}_{0}g_a(t)dt$ en est par théorème une primitive $C^1$ . Vu la formule établie en d., la fonction $f_a$ est donc de classe $C^ 1$ sur ]-R, R[, de dérivée $g_a$ .

9.a. Pour $k \in \mathbb{N}$ ,

$\forall n\geq k, {\begin{pmatrix} n\\ k \end{pmatrix}}$

$=\dfrac{n(n - 1)...(n- k + 1)}{k!} \sim \dfrac{n^k}{k!}, n\longrightarrow \infty$

On a donc

$0 \leq n^k |a_n| r^n \sim k!r^k.{\begin{pmatrix} n\\ k \end{pmatrix}}|a_n|r^{n-k}, n \longrightarrow \infty$

Par suite, les séries $\sum_n n^k |a_n| r^n$ et $\sum_n {\begin{pmatrix} n\\ k \end{pmatrix}}|a_n| r^{n-k}$ sont de même nature. Dans ces conditions,la suite $(a_n)_n$ appartient à A(r) si, et seulement si, la série $\sum_n {\begin{pmatrix} n\\ k \end{pmatrix}}|a_n| r^{n-k}$ converge pour tout $k \in \mathbb{N}$ .

b. On montre par récurrence sur $k \geqslant 0$ que pour toute suite $(a_n)_n \in B(R)$ , la fonction $f_a$ est de classe $C^k$ sur ]-R, R[ avec :

$\forall x \in ]-R, R[, f_a^{(k)}(x)$

$= k!\sum_{n=k}^{\infty} {\begin{pmatrix} n\\ k \end{pmatrix}}a_n x^{n-k}$

Le résultat a été établi au rang k = 0 dans la question 7.. S’il est prouvé à un rang k > 0 et si $(a_n)_n$ est une suite de B(R) alors, d’après l’hypothèse de récurrence appliquée (cf. remarque suivant la question 3.) à la suite $((n+1)a_{n+1})_n$ , la fonction

$g_a : x \longrightarrow \sum_{n=1}^{\infty}n a_n x^{n-1}$

$=\sum_{n=0}^{\infty}(n+1) a_{n+1} x^n$

est de classe $C^k$ sur ]-R, R[, avec :

$\forall x\in ]-R, R[,g_a^{(k)}(x)$

$=k!\sum_{n=k}^{\infty} {\begin{pmatrix} n\\ k \end{pmatrix}}(n+1)a_{n+1} x^{n-k}$

$=(k+1)!\sum_{n=k}^{\infty} {\begin{pmatrix} n+1\\ k+1 \end{pmatrix}}a_{n+1} x^{n-k}$

$=(k+1)!\sum_{n=k+1}^{\infty} {\begin{pmatrix} n\\ k+1 \end{pmatrix}}a_{n} x^{n-(k+1)},$

d’où le résultat d’après 8.e. : $f_a$ est de classe $C^{k+1}$ sur ]-R, R[ avec $f_a^{(k+1)} = g_a^{(k)}$ .

c. En évaluant en x = 0 la formule établie en b., on obtient :

$\forall k\in \mathbb{N}, a_k=\dfrac{f_a^{(k)}(0)}{k!}$

10.a. On a :

$\forall x\in \mathbb{R}, f_\alpha(x)=\sum_{n=0}^{\infty}\dfrac{x^n}{n!}=e^x$

et $f_\alpha^{(k)}(1) = e$ pour tout $k \in \mathbb{N}$ .

b. On a :

$\forall k\in ]-\dfrac{1}{\lambda}, \dfrac{1}{\lambda}[ f_\beta(x)$

$=\sum_{n=0}^{\infty}\lambda^n x^n$

$=\dfrac{1}{1 -\lambda x}$

Il apparaît que la fonction $f_\beta$ est de classe $C^\infty$ sur $]-\dfrac{1}{\lambda}, \dfrac{1}{\lambda}[$ avec, par récurrence immédiate :

$\forall x\in \mathbb{N}, \forall x\in ]-\dfrac{1}{\lambda}, \dfrac{1}{\lambda}[ f_\beta^(k) (x)$

$=\dfrac{k! \lambda^k}{(1 -\lambda x)^{k+1}}$

En appliquant, pour $0 < \varrho < \dfrac{1}{\lambda}$ , la question 9.b. à la suite $\beta \in B(\varrho)$ , on obtient donc :

$\forall x\in ]-\varrho, \varrho[, \sum_{n=k}^{\infty}{\begin{pmatrix} n\\ k \end{pmatrix}} (\lambda x)^{n-k}$

$=\dfrac{f_\beta^(k) (x)}{k!\lambda^k}$

$=\dfrac{1}{(1-\lambda x)^{k+1}}$

avec convergence de la série, puis le résultat s’étend à tout $x \in ]-\dfrac{1}{\lambda}, \fdrac{1}{\lambda}[$ puisque $\varrho$ est quelconque dans $]0, \dfrac{1}{\lambda}[$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Partie 3 : Formule de réciprocité

11.a. En appliquant la formule de Taylor avec reste intégral entre 1 et 0 à la fonction fa, de classe $C^{\infty}$ sur ]-R, R[ avec $R > 1$ d’après 9.b., il vient pour $N \in \mathbb{N}$ :

$f_a(0)=\sum_{k=0}^{N} \dfrac{f_a^{(k)} (1)}{k!}(-1)^k+ \int^{0}_{1}\dfrac{(-t)^N}{N!}f_a^{(N+1)}(t)dt$

= $\sum_{k=0}^{N}(-1)^k b_k +(-1)^{N+1} \int^{1}_{0}\dfrac{t^N}{N!}f_a^{(N+1)} (t)dt$

b. Toujours d’après la question 9.b., on a :

$\forall k\in \mathbb{N}, \forall x\in [0,R[, f_a^{(k)} (x)$

$=k! \sum_{n=k}^{\infty} {\begin{pmatrix} n\\ k \end{pmatrix}}a_n x^{n-k}\geq 0$

Par suite, les dérivées successives de $f_a$ sont positives et croissantes sur [0, R[. Dès lors,

$\forall N\in \mathbb{N}, 0\leq \int^{1}_{0}\dfrac{t^N}{N!}f_a^{(N+1)} (t)dt \leq$

$\int^{1}_{0}\dfrac{t^N}{N!}f_a^{(N+1)}(1)dt=$

$\dfrac{f_a^{(N+1)}(1)}{(N+1)!}=$

$b_{N+1}\leq b_{N+1}\varrho^{N+1}$

où le membre de droite converge vers 0 lorsque $N\longrightarrow \infty$ par hypothèse. Par conséquent,

$\lim_{N\longrightarrow \infty}\int^{1}_{0}\dfrac{t^N}{N!}f_a^{(N+1)} (t)dt=0$

c. D’après les questions a. et b., la série $\sum_k (-1)^k b_k$ converge avec :

$\sum_k ^{\infty}(-1)^k b_k=f_a(0)=a_0$

12.a. Il s’agit là encore d’une application directe de la formule de Taylor avec reste intégral, comme en 11.a., cette fois-ci à la fonction $f^(s)$

b. Comme en 11.b., la positivité et la croissance de $f_a ^{(N+s+1)}$ sur [0, R[ amènent :

$\forall N\in \mathbb{N}, 0\leq \int^{1}_{0}\dfrac{t^N}{N!}f_a^{(N+s+1)} (t)dt$

$\leq \dfrac{f_a^{N+s+1}(1)}{(N+1)!}$

$=b_{N+s+1}\varrho^{N+s+1}\dfrac{(N+s+1)!}{(N+1)!}\dfrac{1}{\varrho^{N+s+1}}$

c. Au second membre de l’inégalité établie en b., $b_{N+s+1}\varrho^{N+s+1}$ tend vers 0 lorsque $N \longrightarrow \infty$ par hypothèse, ainsi que

$\dfrac{(N+s+1)!}{(N+1)!}\dfrac{1}{\varrho^{N+s+1}}$

$=\dfrac{(N + s + 1) .... (N + 2)}{\varrho^{N+s+1}}$

$\sim \dfrac{N^s}{\varrho^{N+s+1}}, N \longrightarrow \infty$

car $\varrho > 1$ . Il en ressort par encadrement que

$\lim_{N\longrightarrow \infty}\int^{1}_{0}\dfrac{t^N}{N!}f_a^{(N+s+1)} (t)dt=0$

d. Des questions a. et c., on déduit la convergence de la série de terme général

$(-1)^k \dfrac{f_a ^{(k+s)}(1)}{k!}=$

$(-1)^k \dfrac{(k + s)!}{k!}b_{k+s}=$

$s!(-1)^k {\begin{pmatrix} k+s\\ s \end{pmatrix}}b_{k+s}, k \geq 0$

avec, d’après 9.c. :

$a_s=\dfrac{f_a ^{(s)}(0)}{s!}=$

$\dfrac{1}{s!} \sum_{k=0}^{\infty}(-1)^k \dfrac{f_a ^{(k+s)}(1)}{k!}=$

$\sum_{k=0}^{\infty}(-1)^k{\begin{pmatrix} k+s\\ s \end{pmatrix}}b_{k+s}=$

$\sum_{n=s}^{\infty}(-1)^{n-s}{\begin{pmatrix} n\\ s \end{pmatrix}}b_n$

13.a. Dans les conditions de l’énoncé, la fonction fa est polynomiale de degré inférieur ou égal à d.

b. D’après a., on a $f_a ^{(n)}= 0$ et donc $b_n = 0$ pour tout $n \geq d+1$ , si bien que la condition (H) est réalisée : la suite $(b_n \varrho^n)_n$ converge vers 0 pour tout réel $\varrho > 1$ .

c. La formule de la question 12.d. s’applique donc et devient :

$\forall N\in [0,d], a_s=$

$\sum_{n=s}^{d}(-1)^{n-s}{\begin{pmatrix} n\\ s \end{pmatrix}}b_n$

COURS A DOMICILE

Des cours sur mesure de qualité

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Partie 4 : Application aux variables aléatoires discrètes

14.a. La série $\sum_{n} a_n =\sum_{n}P(X = n)$ étant convergente, son terme général converge vers 0 : la suite $(a_n)_n$ appartient à B(1).

b. Dans ces conditions, la fonction $G_X = f_a$ est de classe $C^\infty$ sur ]-1, 1[ d’après la question 9.b.

15.a. On a :

$\forall x\in \mathbb{R}, G_X(x)= e^{-1}\sum_{n=0}^{\infty}\dfrac{x^n}{n!}$

$=e^{x-1}$

Il apparaît que la fonction $G_X$ est de classe $C^\infty$ sur R avec, pour tout $s \in \mathbb{N}, G_X^{(s)}(x)=e^{x-1}$ pour tout $x \in \mathbb{R}$ et en particulier $G_X^{(s)} (1) = 1$ .

b. Dans les conditions de l’énoncé, on a $b_n = \dfrac{1}{n!}$ pour tout $n \in \mathbb{N}$ si bien que $(b_n \varrho^n)_n$ converge vers 0 pour tout $\varrho > 1$ comme terme général d’une série exponentielle convergente : l’hypothèse (H) est donc satisfaite. Par suite, la formule de la question 12.d. s’applique et donne :

$\forall s \in \mathbb{N}, P(X=s)=a_s$

$= \sum_{n=s}^{\infty}{\begin{pmatrix} n\\ s \end{pmatrix}} \dfrac{1}{n!}$

$=\sum_{n=s}^{\infty}\dfrac{(-1)^{n-s}}{s!(n-s)!}$

$=\dfrac{1}{s!}\sum_{n=0}^{\infty}\dfrac{(-1)^{k}}{k!}$

$=\dfrac{e^{-1}}{s!}$

La variable X suit donc la loi de Poisson P(1).

16.a. Il vient pour tout $n \in \mathbb{N}$

$a_n = P(X = n) = P(X + 1 = n + 1) = pq^n$ et :

$\forall x \in ]-\dfrac{1}{q}, \dfrac{1}{q}[, G_X(x)$

$= p \sum_{n=0}^{\infty} q^n x^n$

$= \dfrac{p}{1-qx}$

Il apparaît que $G_X$ est de classe $C^\infty$ sur $]-\dfrac{1}{q}, \dfrac{1}{q}[$ avec :

$\forall s \in \mathbb{N}, \forall x\in ]-\dfrac{1}{q}, \dfrac{1}{q}[,G_X^{(s)}(x)$

$=\dfrac{pq^s s!}{(1-qx)^{s+1}}$

En particulier, $G_X^{(s)} (1) = s!(\dfrac{q}{p})^s$ pour tout $s \in \mathbb{N}$ .

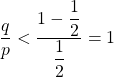b. La fonction $p \longrightarrow \dfrac{q}{p}=\dfrac{1}{p}-1$ est décroissante sur ]0, 1[ si bien que pour $p > \dfrac{1}{2}$ , on a $\dfrac{q}{p}<\dfrac{1-\dfrac{1}{2}}{\dfrac{1}{2}}=1$ . Sous les conditions de l’énoncé, on a $b_n =(\dfrac{q}{^p})^n$ pour tout $n \in \mathbb{N}$ , si bien que $(b_n\varrho^n)_n$ converge vers 0 pour tout $\varrho$ tel que $1 < \varrho < \dfrac{p}{q}$ : l’hypothèse (H) est donc vérifiée. La question 12.d. s’applique alors et donne :

$\forall s \in \mathbb{N}, P(X=s)=a_s$

$=\sum_{n=s}^{\infty}(-1)^{n-s}{\begin{pmatrix} n\\s \end{pmatrix}} (\dfrac{q}{p})^n$

$=(\dfrac{q}{p})^s \sum_{n=s}^{\infty} {\begin{pmatrix} n\\s \end{pmatrix}}(-\dfrac{q}{p})^{n-s}$

$=(\dfrac{q}{p})^s \dfrac{1}{(1+\dfrac{q}{p})^{s+1}}= pq^s$

d’après 10.b. sachant $|\dfrac{q}{p}| < 1$ . Il en ressort comme en a. que X + 1 suit la loi géométrique G(p).

17. On note $P_d$ le sous-espace vectoriel de $R^R$ constitué des fonctions polynomiales de degré inférieur ou égal à d.

a. Les polynômes $H_0$ , $H_1$ , …. , $H_d$ sont non nuls et de degrés deux-à-deux distincts : ils forment donc une famille libre de $P_d$ , formée de $d + 1 = dim P_d$ vecteurs, c’est-à-dire une base de $P_d$ .

b. C’est immédiat : $\Delta$ est clairement linéaire sur $P_d$ et à valeurs dans $P_d$ .

c. On a bien sûr $\Delta(H_0) = 0$ et, pour $s \in [1,d]$ ,

$\forall x \in \mathbb{R}, \Delta(H_s)(x)$

$=\dfrac{(x + 1)x... (x- s + 2)}{s!}$

$- \dfrac{(x + 1)x... (x- s + 1)}{s!}$

$=\dfrac{(x - 1)x... (x- s + 2)}{s!}((x + 1)$

$- (x - s + 1))$

$= \dfrac{(x - 1)x... (x- s + 2)}{(s-1)!}$

$=H_{s-1}(x)$

ainsi que $H_s(0) = 0$ .

d. On commence par vérifier la formule pour un polynôme $P = H_k$ , $k \in [0, d]$ . Or, en itérant le résultat obtenu en c., il vient :

$\forall s\in[0, d], \Delta^s(H_k)$

$=\begin{cases} H_{k-s} \qquad si \qquad s \leqslant k\\ 0 \qquad si \qquad s > k \end{cases}$

si bien que

$\forall s\in[0, d], \Delta^s(H_k)(0)$

$=\begin{cases} 1 \qquad si \qquad s = k\\ 0 \qquad sinon \end{cases}$

d’où finalement

$\sum_{s=0}^{\infty}[\Delta^s(H_s)(0)]H_s=H_k$

Puisque les applications $P\longrightarrow P$ et $P \longrightarrow \sum_{s=0}^{d}[\Delta^s(P)(0)]H_s$ sont linéaires sur $P_d$ et coïncident comme on vient de le voir sur les vecteurs de la base $(H_0,H_1,....,H_d)$ , elles sont donc égales :

$\forall P\in P_d, P$

$=\sum_{s=0}^{d} [\Delta^s(P)(0)]H_s$

e. Il sufit d’appliquer la formule de la question d. au polynôme $P=e_k$

$\forall k \in [0, d],\quad \forall n \in \mathbb{N}, \quad n^k$

$= e_k(n)$

$= \sum_{s=0}^{d}[\Delta^s(e_k)(0)]H_s(n)$

f. Pour $k \in [0, d]$ , il vient par transfert et d’après e.

$E(X^k)=\sum_{s=0}^{d}n^k a_n$

$=\sum_{n=0}^{d}\sum_{s=0}^{d}[\Delta^s(e_k)(0)]H_s(n)a_n$

$=\sum_{n=0}^{d}[\Delta^s(e_k)(0)](\sum_{n=0}^{d}H_s(n)a_n)$

où :

$\forall s \in [0, d], \sum_{n=0}^{d}[\Delta^s(e_k)(0)](H_s(n)a_n)$

$=\sum_{n=0}^{d}\dfrac{n(n - 1)....(n - s + 1)}{s!}a_n$

$=\dfrac{G_X^(s)(1)}{s!}=b_s$

ce qui conduit au résultat :

$E(X^k)=[\Delta^s(e_k)(0)]b_s$

g. En calculant les valeurs de $\Delta^s(e_k)(0)$ , $0\leqslant k$ , $s \leqslant 2$ , on explicite les relations de la question f. pour $k \in \lbrace{0, 1, 2}\rbrace$ , qui permettent d’accéder aux valeurs de $b_0, b_1, b_2$ :