Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet HEC Maths 1 ECS 2018
Revenir à tous les corrigés des annales maths BCE
Partie Préliminaire
1/ a/ Pour tout ![]() , la fonction
, la fonction ![]() définie sur
définie sur ![]() par :
par :
![]() est continue et positive sur
est continue et positive sur ![]() ,
,
et en ![]()
![]() ;
;
Par comparaison à l’intégrale de Riemann convergente
![]() ,
, ![]() converge
converge
donc ![]() converge.
converge.
b/ Soit ![]() une densité de la loi normale
une densité de la loi normale
![]() , et
, et ![]() une VAR suivant cette loi normale ;
une VAR suivant cette loi normale ;
![]()
=![]()
car ![]() est paire et
est paire et ![]() ;
;
![]()
=![]()
=![]()
car ![]() est paire
est paire
Donc ![]()
=![]()
=![]()
![]()
=![]()
=![]()
=![]() .
.
Ainsi, ![]()
=![]()
=![]()
et ![]()
2/ La fonction qui à ![]() associe
associe ![]() est continue, positive, et dominée par
est continue, positive, et dominée par ![]() ;
;
Ainsi ![]() converge absolument, donc converge ;
converge absolument, donc converge ;
De même ![]() converge absolument.
converge absolument.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie I. Calcul d’une fonction auxiliaire
3/ a/ D’après l’inégalité de Taylor-Lagrange à l’ordre 0 en 0, pour la fonction
![]() qui est de classe
qui est de classe ![]() sur
sur ![]() :
:
![]()
avec ![]()
=![]()
=![]() ,
,
donc : ![]()
b/ ![]()
=![]() ;
;
pour ![]() , prenons
, prenons
![]()
et ![]() ,
,
On a bien ![]()
et ![]() d’où :
d’où :
![]()
=![]()
c/ Soit ![]() ;
;
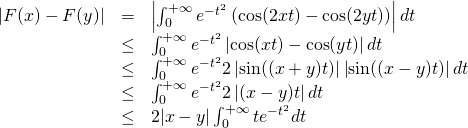
Ainsi ![]()
donc :
![]()
![]() est continue en
est continue en ![]()
et ceci pour tout ![]() .
.
4/ a/ Par l’inégalité de Taylor-Lagrange à l’ordre 1 en 0, pour la fonction ![]() qui est de classe
qui est de classe ![]() sur
sur ![]() :
:
![]()
avec ![]() , donc :
, donc :
![]()
b/ Soit ![]() ;
;
![]()
=![]()
avec :
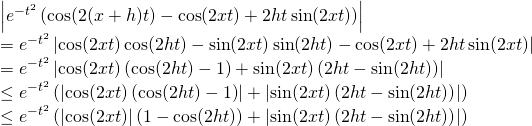
On remarque que ![]() qui est le terme général d’une intégrale convergente d’après la partie préliminaire ;
qui est le terme général d’une intégrale convergente d’après la partie préliminaire ;
![]()
Ainsi ![]() converge comme somme d’intégrales convergentes, donc :
converge comme somme d’intégrales convergentes, donc :
![]() est absolument convergente ;
est absolument convergente ;
D’après l’inégalité triangulaire :
![]()
c/ D’après les inégalités établies dans la question précédente,
![]()
et
![]()
donc :
![]()
Cette dernière intégrale converge de la même manière que la deuxième de la question 2), et ne dépend pas de ![]() , ce qui justifie de remplacer sa valeur par une constante
, ce qui justifie de remplacer sa valeur par une constante ![]() :
:
![]()
5/ a/ Soit ![]() ;
; ![]()
donc : ![]()
donc ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
Ceci étant vrai pour tout ![]() ,
, ![]() est dérivable sur
est dérivable sur ![]() et
et ![]()
b/ Soit ![]() ;
; ![]() .
.
Intégration par parties sur le segment ![]() (
(![]() ), avec
), avec
![]()
les fonctions ![]() et
et ![]() étant bien de classe
étant bien de classe ![]() sur
sur ![]() :
:
![Rendered by QuickLaTeX.com \begin{array}{lll} \ds \int_0^{A} -2te^{t^2}\sin(2xt)dt &=& \ds \left[ \sin(2xt)e^{-t^2} \right]_0^{A} -2x\int_0^{A} \cos(2xt)e^{-t^2}dt \\ &=& \ds \sin(2Ax)e^{-A^2} -2x \int_0^{A} \cos(2xt)e^{-t^2}dt \end{array}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ce20d4c1e457a556558b65cd05831a4a_l3.png)
donc :
![]()
donc : ![]()
c/ Soit ![]() la fonction définie sur
la fonction définie sur ![]() par :
par : ![]() .
.
![]() est dérivable et
est dérivable et ![]()
Ainsi, ![]() est constante donc :
est constante donc : ![]()
Ainsi, ![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
II. Fonction de Dirichlet
6/ a/ Sur ![]() :
: ![]() donc
donc ![]() ne s’annule pas, et
ne s’annule pas, et ![]() est continue comme quotient de fonctions continues avec un dénominateur non nul.
est continue comme quotient de fonctions continues avec un dénominateur non nul.
En 0 : ![]() ,
,
donc : ![]()
b/ 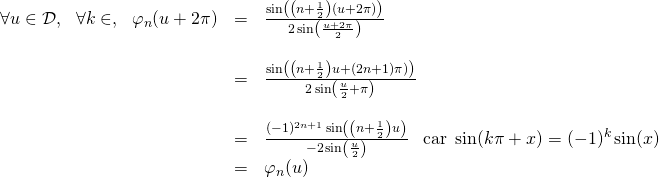
Ainsi ![]() est
est ![]() -périodique, donc :
-périodique, donc : ![]()
![]() est bien prolongeable par continuité sur
est bien prolongeable par continuité sur ![]() .
.
c/ ![]() est paire comme quotient de fonctions impaires.
est paire comme quotient de fonctions impaires.
7/ a/ ![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() , donc :
, donc :
si ![]() :
: ![]() donc
donc ![]() ;
;
si ![]() :
:
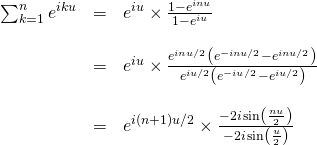
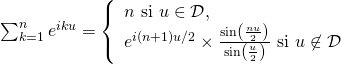
b/ Si ![]() :
: ![]() donc
donc ![]() ;
;
si ![]() :
:
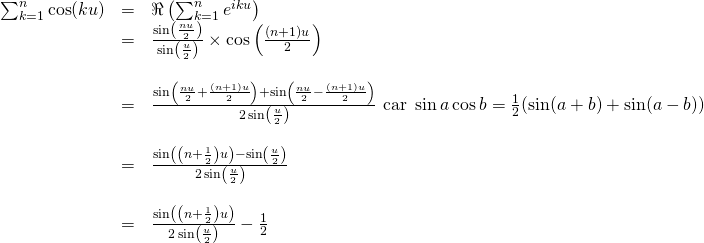
Dans tous les cas, ![]()
c/ ![]()
![]()
8/ Soit ![]() et
et ![]() ; alors
; alors ![]() , donc :
, donc :
![]()
La relation de Chasles donne :
![]()
Effectuons les deux changements de variables suivantes, affines donc licites :
Première intégrale : ![]() donne :
donne : ![]() .
.
Deuxième intégrale : ![]() donne :
donne : ![]() .
.
Ainsi ![]()
Partie III. Formule sommatoire de Poisson
9/ a/ Pour tout ![]() ,
,
![]()
or, lorsque ![]() ,
, ![]() , et
, et ![]() , donc :
, donc :
![]() donc :
donc : ![]()
donc : ![]() et par conséquent
et par conséquent ![]()
Par critère de comparaison à une série de Riemann convergente, ![]() converge et de même pour
converge et de même pour ![]() .
.
b/ ![]() étant paire,
étant paire,
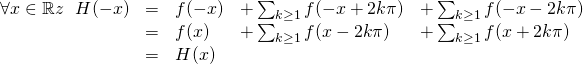
Ainsi, ![]() est paire et donc sa dérivée est impaire
est paire et donc sa dérivée est impaire
10/ a/ Pour ![]() ,
,
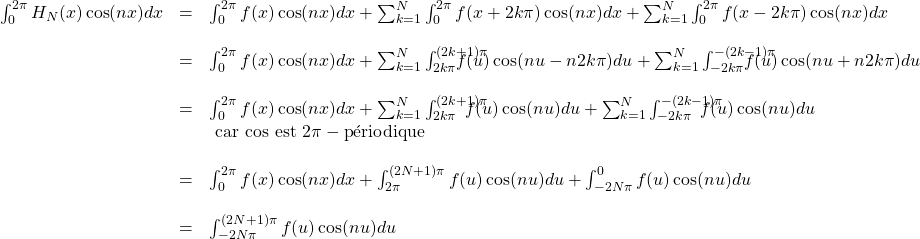
b/ ![]() ;
;
cette intégrale est donc absolument convergente d’après la partie préliminaire;
![]() est paire ;
est paire ;
donc ![]() converge et vaut
converge et vaut ![]() ;
;
donc ![]()
et ![]()
c/ Pour tout ![]() et
et ![]() :
:
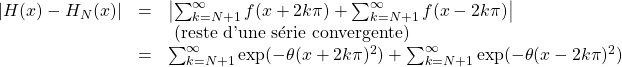
![]()
![Rendered by QuickLaTeX.com \[\begin{array}{ll} & 0 \leq x \leq 2\pi \\ \Rightarrow &\ds 2k\pi \leq x+2k\pi \leq (2k+1)\pi \\ \Rightarrow & \ds -\theta (2k+1)^2\pi^2 \leq -\theta (x+2k\pi)^2 \leq -\theta (2k\pi)^2 \\ \Rightarrow & \ds \exp(-\theta (2k+1)^2\pi^2 ) \leq f(x+2k\pi) \leq \exp(-\theta 4k^2\pi^2 ) \\ &\\ \Rightarrow & \ds ${0 \leq \sum_{k=N+1}^{\infty} f(x+2k\pi) \leq \sum_{k=N+1}^{\infty} \exp(-\theta 4k^2\pi^2 )}$ \\ \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-54e4d4ab4347f354774518d5abba0070_l3.png)
et
![Rendered by QuickLaTeX.com \[\begin{array}{ll} & 0 \leq x \leq 2\pi \\ \Rightarrow &\ds -2k\pi \leq x-2k\pi \leq -(2k-1)\pi <0 \\ \Rightarrow & \ds (2k-1)^2\pi^2 \leq (x-2k\pi)^2 \leq (2k\pi)^2 \\ \Rightarrow & \ds \exp(-\theta (2k)^2\pi^2 ) \leq f(x+2k\pi) \leq \exp(-\theta (2k-1)^2\pi^2 ) \\ \Rightarrow & \ds \sum_{k=N+1}^{\infty} f(x-2k\pi) \leq \sum_{k=N+1}^{\infty} \exp(-\theta (2k-1)^2\pi^2 ) \\ \Rightarrow & \ds \sum_{k=N+1}^{\infty} f(x-2k\pi) \leq \sum_{j=N}^{\infty} \exp(-\theta (2j+1)^2\pi^2 ) \\ &\\ \Rightarrow & \ds ${ 0\leq \sum_{k=N+1}^{\infty} f(x-2k\pi) \leq \sum_{j=N}^{\infty} \exp(-\theta 4j^2\pi^2 )}$ \\ \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-6dfc25be0d7a08e8612a14d979bfb591_l3.png)
Ainsi,
![]()
d/ D’après la question précédente,
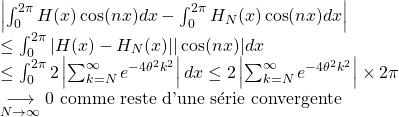
donc : ![]()
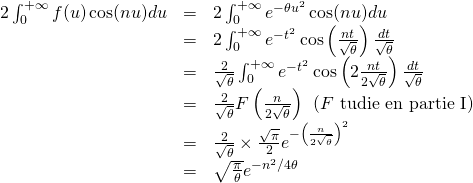
donc : ![]()
11/ ![]() .
.
a/ 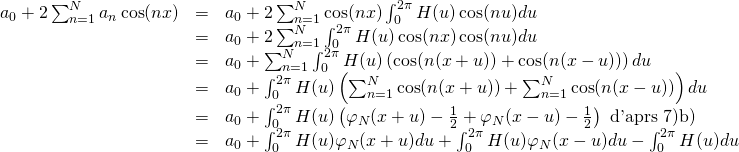
or ![]() , donc :
, donc :
![]()
b/ Transformons ![]() à l’aide du changement de variable affine
à l’aide du changement de variable affine ![]() :
:
![]()
Or ![]() est
est ![]() périodique, car
périodique, car
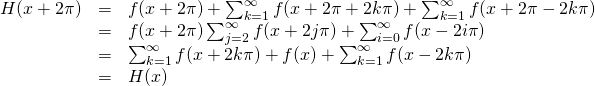
![]() est également
est également ![]() périodique d’après le résultat établi en 6)b), donc la fonction \\
périodique d’après le résultat établi en 6)b), donc la fonction \\ ![]() est
est ![]() périodique, et ainsi, d’après la question 8),
périodique, et ainsi, d’après la question 8),
![]()
et de même pour ![]() .
.
Par conséquent : ![]()
c/ Sur ![]() :
: ![]() est de classe
est de classe ![]() (admis) donc continue ;
(admis) donc continue ; ![]() est continue et ne s’annule pas, donc
est continue et ne s’annule pas, donc ![]() est continue par quotient.
est continue par quotient.
En 0 : ![]() étant de classe
étant de classe ![]() sur
sur ![]() , elle est notamment dérivable en
, elle est notamment dérivable en ![]() et y admet un DL d’ordre 1 :
et y admet un DL d’ordre 1 :
![]()
donc : ![]()
Par ailleurs, lorsque ![]() ,
, ![]() , donc :
, donc :
![]()
En ![]() :
:
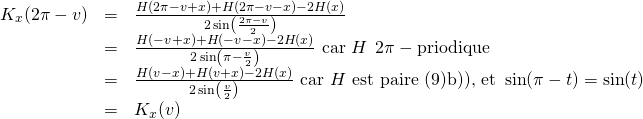
donc : ![]() donc
donc ![]() continue en
continue en ![]()
(par le changement de variable ![]() .)
.)
d/ D’après 7)c),
![]()
donc :
![]()
donc :
![Rendered by QuickLaTeX.com \[\begin{array}{l} \ds a_0+ 2\sum_{n=1}^N a_n\cos(nx)-2\pi H(x) \\ \ds = \int_0^{2\pi} \left( \frac{H(v+x)+H(v-x)}{2\sin(v/2)} \right) \times \sin \left( \left( N+\frac 12 \right)v\right) dv - 2H(x)\int_0^{2\pi} \frac{\sin \left( \left( N+\frac 12\right)v\right)}{2\sin \left(\frac v2\right)}dv \\ \ds = \int_0^{2\pi} \left( \frac{H(v+x)+H(v-x)-2H(x)}{2\sin(v/2)} \right) \times \sin \left( \left( N+\frac 12 \right)v\right) dv \\ \ds =\int_0^{2\pi} K_x(v) \sin \left( \left( N+\frac 12\right)v\right) dv \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-04ff1221df22809d2bdd7fc2c22d61d9_l3.png)
12/ a/
![]()
(Intégration par parties avec ![]() et
et ![]() )
)
![]() donc
donc ![]() ;
;
![]() ,
,
donc ![]() .
.
Par somme, ![]()
b/
![Rendered by QuickLaTeX.com \[\begin{array}{lll} \ds \frac{1}{\sqrt{\pi\theta}} \left(\frac 12 +\sum_{n=1}^{\infty} \exp \left( -\frac{n^2}{4\theta}\right)\cos(nx) \right) &=& \ds \frac{1}{2\sqrt{\pi\theta}} + \frac{1}{2\pi} \sum_{n=1}^{\infty} a_n \cos(nx) \\ &=& \ds \frac{1}{2\pi} \left( a_0 + 2 \sum_{n=1}^{\infty} a_n \cos(nx) \right) \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1f22e204b3b34ff3cb535e52fa9e7b25_l3.png)
Or, d’après 11)d),
![Rendered by QuickLaTeX.com \[a_0+2\sum_{n=1}^N a_n\cos(nx) -2\pi H(x) = \int_0^{2\pi} K_x(v)\sin \left( \left(N+\frac 12 \right) v \right) dv\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-aaca84f697fd24b4fb00d2e145a67339_l3.png)
d’après 11)c), ![]() est continue sur
est continue sur ![]() ;
;
d’après 12)a), ![]()
donc ![]()
donc : ![]()
Partie IV. Une application probabiliste de la formule sommatoire de Poisson
13/ ![]() s=s+2 ; j=1
s=s+2 ; j=1
![]() i est le nombre de lancers effectués depuis le début de la partie et jusqu’à l’arrêt du jeu.
i est le nombre de lancers effectués depuis le début de la partie et jusqu’à l’arrêt du jeu.
![]() v est un indicateur permettant de savoir quel est le joueur en cours (et donc qui gagne).
v est un indicateur permettant de savoir quel est le joueur en cours (et donc qui gagne).
Dans les initialisations ajouter : ![]()
Dans la boucle ![]() while, avant l’instruction if j>s …, ajouter :
while, avant l’instruction if j>s …, ajouter :
if v==1 then
k=k+1
end
Méthode de Monte-Carlo : une valeur approchée est la fréquence de l’événement « ![]() vainqueur » sur un grand nombre de simulations :
vainqueur » sur un grand nombre de simulations :
N=10000 ;
f=0 ;
p=input(‘entrez probabilité de Pile’) ;
for k=1:N
if jeu(p)==1 then
f=f+1
end
end
disp(f/N)
14/ a/ ![]() signifie qu’il y a un vainqueur (le jeu se termine) ;
signifie qu’il y a un vainqueur (le jeu se termine) ; ![]() signifie qu’il n’y a pas de vainqueur : le jeu continue indéfiniment, ce qui signifie que « Pile » ne sort jamais.
signifie qu’il n’y a pas de vainqueur : le jeu continue indéfiniment, ce qui signifie que « Pile » ne sort jamais.
Notons, pour ![]() ,
, ![]() l’événement : « il n’y a eu que des Face lors des
l’événement : « il n’y a eu que des Face lors des ![]() premiers lancers ».
premiers lancers ».
![]() est une suite décroissante d’événements, donc, par le théorème de limite monotone~:
est une suite décroissante d’événements, donc, par le théorème de limite monotone~:
![]()
donc :
![]()
![]() est le nombre total de lancers effectués jusqu’à l’arrêt du jeu (obtention du premier « Pile »). D’après ce qui précède,
est le nombre total de lancers effectués jusqu’à l’arrêt du jeu (obtention du premier « Pile »). D’après ce qui précède, ![]() a une valeur finie presque s\^urement et :
a une valeur finie presque s\^urement et :
![]()
b/ Notons ![]() l’événement : le joueur
l’événement : le joueur ![]() gagne dès le premier lancer (autrement dit, « Pile » sort au premier lancer). Alors
gagne dès le premier lancer (autrement dit, « Pile » sort au premier lancer). Alors
![Rendered by QuickLaTeX.com \[\begin{array}{lc} & A_1 \subset H \\ \mbox{donc } & P_p(A_1) \leq P_p(H) \leq 1 \\ \mbox{donc } & p \leq P_p(H) \leq 1 \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b4cdc0af0bf23aaf6b25fe4a12914cd9_l3.png)
Par théorème d’encadrement, ![]()
15/ a/ Les séquences sont de longueur impaire : 1,3,5 …
Ainsi, la séquence numéro ![]() est de longueur
est de longueur ![]() , avec les conventions suivantes :
, avec les conventions suivantes :
La première porte le numéro 0, elle ne comporte que le premier lancer (effectué par le joueur ![]() )
)
![]() joue les séquences de numéro
joue les séquences de numéro ![]() pair et
pair et ![]() les séquences de numéro
les séquences de numéro ![]() impair
impair
Lorsque la séquence numéro ![]() commence, le nombre total de lancers déjà effectués est donc :
commence, le nombre total de lancers déjà effectués est donc :
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{j-1} (2k+1) = 2 \sum_{k=0}^{j-1}k + j =j(j-1)+j = j^2\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-98be565ce77b3cd820af218619c7d1ec_l3.png)
Par conséquent, ![]()
Or, {![]() effectue les séquences de numéro pair :
effectue les séquences de numéro pair : ![]() } donc :
} donc :
Le premier lancer de la séquence est le lancer numéro ![]() ;
;
La séquence est de longueur ![]() donc le dernier lancer (s’il a lieu) porte le numéro
donc le dernier lancer (s’il a lieu) porte le numéro ![]()
Ainsi, les valeurs de ![]() sont incluses dans l’ensemble
sont incluses dans l’ensemble ![]() .
.
b/ Notons ![]() l’événement : «
l’événement : « ![]() gagne lors de la séquence numéro
gagne lors de la séquence numéro ![]() « .
« .
![Rendered by QuickLaTeX.com \[A_n= F_1\cap \cdots \cap F_{4n^2} \cap \left( \bigcup_{k=1}^{4n+1} (\underbrace{F\cdots F}_{\mbox{k-1 fois}}P) \right)\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3d192456a1fb7bf69e295e0a22bdb875_l3.png)
donc, la réunion étant disjointe et les lancers indépendants,
![Rendered by QuickLaTeX.com \[\begin{array}{ll} \ds P_p(A_n) &= \ds (1-p)^{4n^2} \times \left( \sum_{k=1}^{4n+1} (1-p)^{k-1}p \right) \\ &= \ds (1-p)^{4n^2} \times \frac{1-(1-p)^{4n+1}}{1-(1-p)} \\ &=\ds (1-p)^{4n^2}-(1-p)^{4n^2+4n+1} \\ \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-914a52bf30b7cc4cab3c054bb74bd9b7_l3.png)
![]() étant l’union disjointe des
étant l’union disjointe des ![]() ,
,
![]()
![]() prend ses valeurs dans l’ensemble complémentaire de celles de
prend ses valeurs dans l’ensemble complémentaire de celles de ![]() : les séries démarrent aux lancers
: les séries démarrent aux lancers ![]() et terminent aux lancers
et terminent aux lancers ![]() :
:
![]()
16/ a/ D’après 12)b),
![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{\pi\theta}} \left( \frac 12 +\sum_{n=1}^{\infty} \exp \left( -\frac{n^2}{4\theta}\right) \cos(nx) \right) = e^{-\theta x^2} +\sum_{k=1}^{\infty} e^{-\theta (x+2k\pi)^2} + \sum_{k=1}^{\infty} e^{-\theta (x-2k\pi)^2}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-1880cfd1b1e23f13eb9d4cf3de595195_l3.png)
Appliquons cette égalité avec :
![]() donc
donc ![]()
![]() donc
donc ![]() et
et ![]()
Ainsi,
![Rendered by QuickLaTeX.com \[\begin{array}{ll} \ds \sum_{n=0}^{\infty} (-1)^n (1-p)^{n^2} & \ds = 1 +\sum_{n=1}^{\infty} (-1)^n (1-p)^{n^2} \\ &\ds = \frac 12 + \left( \frac 12 + \sum_{n=1}^{\infty} \cos(nx) \exp \left( -\frac{n^2}{4\theta} \right) \right) \\ &\ds = \frac 12 +\frac{1}{\sqrt{\pi \theta}} \left( e^{-\theta \pi^2} +\sum_{k=1}^{\infty} \exp \left( -\theta (\pi + 2k\pi)^2\right) + \sum_{k=1}^{\infty} \exp \left( -\theta (\pi - 2k\pi)^2\right)\right) \\ & >\ds \frac 12 \mbox{ car sommes de séries à termes strictement positifs} \end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-4650a0d014354cdba49718230aee2645_l3.png)
b/ ![]()
Conclusion : le jeu est inéquitable car ![]() a plus de chance de gagner que
a plus de chance de gagner que ![]() .
.

