Mon parcours pour réussir en maths
Je révise en autonomie
Je progresse avec un prof
Je m’entraîne sur des annales corrigées
Avis Google France
★★★★★ 4,9 sur 5
Corrigé du sujet maths HEC 2017 ECS
Revenir à tous les corrigés des annales maths BCE
Partie 1 : Propriétés des polynômes de Bernstein
1.a ![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
donc
![]() =
=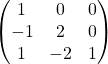
b. ![]() est inversible car il s’agit d’une matrice triangulaire inférieure et ne contient aucun 0 sur la diagonale ;
est inversible car il s’agit d’une matrice triangulaire inférieure et ne contient aucun 0 sur la diagonale ; ![]() est donc une base de
est donc une base de ![]() .
.
c.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
donc ![]() =
=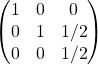
![]() étant une matrice triangulaire inférieure, ses valeurs propres sont les éléments sur la diagonale donc
étant une matrice triangulaire inférieure, ses valeurs propres sont les éléments sur la diagonale donc ![]()
![]() et
et ![]() donc
donc ![]() est inclus dans
est inclus dans ![]() ;
;
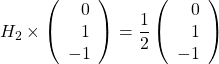
donc ![]() ;
;
La somme des dimensions des espaces propres ne peut pas dépasser 3,
![]()
![]()
![]()
et ![]()
2.a Pour ![]() [\![0\,;n]\!],
[\![0\,;n]\!], ![]() donc le terme non égal à zéro de plus faible degré de
donc le terme non égal à zéro de plus faible degré de ![]() est
est ![]() .
.
Donc, la matrice ![]() de la famille
de la famille ![]() dans la base
dans la base ![]() est une matrice triangulaire inférieure et ses coefficients diagonaux sont les
est une matrice triangulaire inférieure et ses coefficients diagonaux sont les ![]() . Ces coefficients diagonaux sont tous non nuls, donc
. Ces coefficients diagonaux sont tous non nuls, donc ![]() est inversible, d’où
est inversible, d’où ![]() est une base de
est une base de ![]() .
.
2.b. ![]() Pour tout
Pour tout ![]() ,
, ![]() est combinaison linéaire des
est combinaison linéaire des ![]() , donc
, donc ![]() :
: ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
![]() Injectivité : soit
Injectivité : soit ![]() tel que
tel que ![]() , alors
, alors ![]()
Or la famille des ![]() est libre, donc
est libre, donc
![]()
![]() possède alors
possède alors ![]() racines distinctes, or
racines distinctes, or ![]() est de degré inférieur ou égal à
est de degré inférieur ou égal à ![]() , donc
, donc ![]() est le polynôme nul : Ker
est le polynôme nul : Ker![]() donc
donc ![]() est injectif.
est injectif.
![]()
![]() étant un endomorphisme injectif d’un espace de dimension finie,
étant un endomorphisme injectif d’un espace de dimension finie, ![]() est alors un automorphisme de cet espace.
est alors un automorphisme de cet espace.
2.c. ![]() donc
donc ![]()
![]()
![]()
![]()
![]() :
:
![]()
![]() donc
donc
![]()
![]() en enlevant le premier terme nul
en enlevant le premier terme nul
![]()
![]()
![]()
![]()
donc ![]()
2.d. Montrons par récurrence finie sur ![]() :
: ![]() est de degré
est de degré ![]() .
.
![]() Initialisation :
Initialisation : ![]() donc
donc ![]() est vraie et
est vraie et ![]() donc
donc![]() est vraie également.
est vraie également.
![]() Hérédité : soit
Hérédité : soit ![]() tel que
tel que ![]() soit vraie, et notons
soit vraie, et notons ![]() le coefficient de son terme de degré
le coefficient de son terme de degré ![]() . D’après le résultat admis,
. D’après le résultat admis,
![]()
![]()
Le terme de plus haut degré de ![]() est :
est : ![]() ,celui de
,celui de ![]() est :
est : ![]()
Le terme de plus haut degré de ![]() est donc :
est donc : ![]() avec
avec
![]() car
car ![]() et
et ![]()
![]() est donc bien de degré
est donc bien de degré ![]() :
: ![]() est vraie.
est vraie.
2.e. D’après la question précédente, ![]() et
et
![]()
![]()
![]()
Il s’ensuit, par récurrence :
![]() et
et ![]()
![]()
![]()
Notons alors ![]() la matrice de
la matrice de ![]() dans la base
dans la base ![]() ; d’après la question d)
; d’après la question d) ![]() est triangulaire supérieure, elle a pour valeurs propres ses coefficients diagonaux, qui sont les
est triangulaire supérieure, elle a pour valeurs propres ses coefficients diagonaux, qui sont les ![]() .
.
Or ![]() , mais à partir du rang 1 on a :
, mais à partir du rang 1 on a : ![]() , donc tous les autres coefficients diagonaux sont distincts.
, donc tous les autres coefficients diagonaux sont distincts.
On a déjà ![]() donc
donc ![]() ; et pour
; et pour ![]() ,
, ![]() , donc
, donc ![]()
ainsi : ![]() est diagonalisable,
est diagonalisable, ![]() =Vect
=Vect![]() et
et ![]()
3.a ![]() peut être considérée comme la somme de
peut être considérée comme la somme de ![]() Variable Aléatoire Réelle de Bernoulli, indépendantes et de même paramètre
Variable Aléatoire Réelle de Bernoulli, indépendantes et de même paramètre ![]() ; ces variables étant d’espérance
; ces variables étant d’espérance ![]() et admettant une variance, par la loi faible des grands nombres
et admettant une variance, par la loi faible des grands nombres ![]() converge en probabilité vers
converge en probabilité vers ![]() .
.
3.b. ![]() est une fonction continue sur un segment, elle est donc bornée et atteint ses bornes.
est une fonction continue sur un segment, elle est donc bornée et atteint ses bornes.
3.c. Notons que ![]() , donc
, donc ![]() et de même
et de même ![]() . Raisonnons alors par disjonction de cas :
. Raisonnons alors par disjonction de cas :
![]() Si
Si ![]() est réalisé, alors
est réalisé, alors ![]() et
et ![]() , et :
, et :
![]()
![]()
![]()
![]() Si
Si ![]() n’est pas réalisé, alors
n’est pas réalisé, alors ![]() et
et ![]() , et :
, et :
![]()
![]()
3.d. Pour tout ![]() fixé :
fixé :
![]() (linéarité de l’espérance)
(linéarité de l’espérance)
![]() (inégalité triangulaire)
(inégalité triangulaire)
![]() (croissance de l’espérance)
(croissance de l’espérance)
![]()
![]() (car
(car ![]() est une VAR de Bernoulli de paramètre P(A))
est une VAR de Bernoulli de paramètre P(A))
![]() (car
(car ![]()
Or, puisque la suite ![]() converge en probabilité vers
converge en probabilité vers ![]() , et que
, et que ![]() est une fonction continue, alors la suite
est une fonction continue, alors la suite ![]() converge en probabilité vers
converge en probabilité vers ![]() . Ainsi :
. Ainsi : ![]()
Il existe donc un rang ![]() tel que :
tel que : ![]()
on a alors :
![]()
donc ![]() , donc :
, donc :
![]()
Il reste à faire le lien avec ![]() : pour tout
: pour tout ![]() , en remarquant que, pour tout
, en remarquant que, pour tout ![]() et tout
et tout ![]() ,
,
![]()
Ainsi,
![]() donc, par le théorème de transfert,
donc, par le théorème de transfert,
![]() d’où :
d’où :
![]()
4.a Z=grand(1,1, « bin » ,n,z)
4.b. Ce code simule 1000 VAR indépendantes suivant la loi de ![]() , puis calcule la moyenne des valeurs de
, puis calcule la moyenne des valeurs de ![]() prises sur ces variables.
prises sur ces variables.
Par la loi faible des grands nombres, la valeur affichée fournit une valeur approchée de ![]() .
.
Comme 100 peut sans doute être considéré comme un grand nombre, la valeur affichée est également une valeur approchée de ![]() .
.
La méthode utilisée ici est la méthode de Monte Carlo.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Partie 2 : Polynômes d’interpolation de Lagrange
5.a Linéarité évidente
![]() Injectivité : soit
Injectivité : soit ![]() tel que
tel que ![]() , alors
, alors ![]() ;
; ![]() possède alors
possède alors ![]() racines distinctes, or
racines distinctes, or ![]() est de degré inférieur ou égal à
est de degré inférieur ou égal à ![]() , donc
, donc ![]() est nul :
est nul :![]() donc
donc ![]() est injectif.
est injectif.
![]()
![]() étant une application linéaire injective entre deux espaces de même dimension,
étant une application linéaire injective entre deux espaces de même dimension, ![]() est un isomorphisme.
est un isomorphisme.
5.b. Pour tout ![]() ,
, ![]() .
.
![]() est un polynôme de degré inférieur ou égal à
est un polynôme de degré inférieur ou égal à ![]() , admettant
, admettant ![]() racines distinctes ; ainsi il existe un réel
racines distinctes ; ainsi il existe un réel ![]() tel que
tel que
![]()
De plus, ![]() ,
,
Donc ![]() d’où :
d’où :
![]()
5.c. ![]() Symétrie :
Symétrie :
![]()
![]()
![]()
![]() par commutativité du produit des réels.
par commutativité du produit des réels.
![]() Bilinéarité : soit
Bilinéarité : soit ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
![]() est linéaire à gauche, et à droite par symétrie.
est linéaire à gauche, et à droite par symétrie.
![]() Positivité : soit
Positivité : soit ![]() ,
, ![]() .
.
![]() Caractère défini : soit
Caractère défini : soit ![]() tel que
tel que ![]() , alors
, alors ![]() car une somme de termes positifs est nulle ssi ils sont tous nuls.
car une somme de termes positifs est nulle ssi ils sont tous nuls.
![]() admet donc
admet donc ![]() racines distinctes, or
racines distinctes, or ![]() est de degré inférieur ou égal à
est de degré inférieur ou égal à ![]() , donc
, donc ![]() est nul.
est nul.
![]()
![]() base orthonormée :
base orthonormée :
soit ![]() , tel que
, tel que ![]() ,
, ![]() car
car ![]() donc il y a toujours un facteur nul dans chaque terme de la somme.
donc il y a toujours un facteur nul dans chaque terme de la somme.
Soit ![]() ,
,
![]()
La famille ![]() est orthonormée, donc libre ; elle est de cardinal
est orthonormée, donc libre ; elle est de cardinal ![]() , c’est donc une base de
, c’est donc une base de ![]() .
.
5.d. Pour tout polynome ![]() de
de ![]() , de coordonnées
, de coordonnées ![]() dans la base
dans la base ![]() ,
, ![]() ;alors, pour tout
;alors, pour tout ![]() ,
,![]() .
.
![]() a donc pour coordonnées
a donc pour coordonnées ![]() .
.
Ainsi, pour tout ![]() ,
, ![]() a pour coordonnées dans la base
a pour coordonnées dans la base![]() :
: ![]() .
.
donc ![]() =
=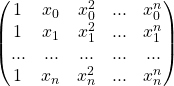
5.e. Si ![]() ,
, ![]()
![]()
![]() .
.
Or ![]() est un isomorphisme d’espaces vectoriels, il existe donc un unique antécédent
est un isomorphisme d’espaces vectoriels, il existe donc un unique antécédent ![]() .
.
D’après la question d,
![]()
6.a ![]() est un polynôme de degré
est un polynôme de degré![]() et
et ![]() de degré
de degré ![]() ,
, ![]() est donc un polynôme de degré
est donc un polynôme de degré![]() ;
; ![]() et
et ![]() ayant les mêmes valeurs en
ayant les mêmes valeurs en ![]() ,
, ![]() admet les
admet les ![]() réels
réels ![]() comme racines distinctes. Il existe donc un réel
comme racines distinctes. Il existe donc un réel ![]() tel que :
tel que :
![]()
et donc en particulier :
![]() .
.
6.b. ![]() Par définition du polynome d’interpolation,
Par définition du polynome d’interpolation, ![]() prend les mêmes valeurs que
prend les mêmes valeurs que ![]() en
en ![]() donc
donc ![]() s’annule en ces
s’annule en ces ![]() points.
points.
![]()
![]() est de classe
est de classe ![]() comme différence de telles fonctions.
comme différence de telles fonctions.
Pour la commodité des notations, on renomme ![]() en :
en : ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() , dérivable sur
, dérivable sur ![]() , et
, et ![]() ; par le théorème de Rolle,
; par le théorème de Rolle,
![]()
![]() est alors une fonction de classe
est alors une fonction de classe ![]() sur
sur ![]() , admettant
, admettant ![]() racines distinctes dans
racines distinctes dans ![]() (car situées dans des intervalles disjoints) :
(car situées dans des intervalles disjoints) : ![]() .
.
![]() Le procédé peut être répété, et ainsi, par récurrence sur
Le procédé peut être répété, et ainsi, par récurrence sur ![]() ,
, ![]() admet
admet ![]() racines distinctes
racines distinctes ![]() .
.
En particulier, ![]() admet une racine
admet une racine ![]() .
.
6.c. ![]() Puisque
Puisque ![]() prend, par définition, la même valeur que
prend, par définition, la même valeur que ![]() en
en ![]() ,
,
on a d’après la question 6.a
![]()
![]() Expression de
Expression de ![]() par les dérivées :
par les dérivées : ![]() est un polynôme de degré
est un polynôme de degré ![]() et son terme de plus haut degré est
et son terme de plus haut degré est ![]() , par conséquent
, par conséquent ![]() .
.
D’autre part, puisque ![]() est de degré
est de degré ![]() ,
, ![]() et donc
et donc
![]()
![]() Or
Or ![]() ,
,
donc ![]() et ainsi :
et ainsi :![]()
On obtient bien :![]()
![]()
![]()
6.d. ![]() Si
Si ![]() ,la question précédente s’applique en prenant
,la question précédente s’applique en prenant ![]() :
:
![]()
![]()
![]() Si
Si ![]() ,
, ![]() donc l’inégalité reste vraie.
donc l’inégalité reste vraie.
Ainsi :![]()
![]()
COURS A DOMICILE
Des cours sur mesure de qualité
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Partie 3 : Exemple d’interpolation et phénomène de Runge
7.a ![]() est de classe
est de classe ![]() sur
sur ![]() car c’est l’inverse d’une fonction polynomiale ne s’annule jamais.
car c’est l’inverse d’une fonction polynomiale ne s’annule jamais.
7.b. Posons ![]() .
.
D’une part, ![]() est paire donc
est paire donc ![]() et :
et :
![]()
![]()
D’autre part, par dérivation des fonctions composées :
![]()
![]()
Par identification, ![]()
![]() donc
donc ![]()
![]()
7.c. Pour tout ![]() tel que
tel que ![]() ,
,
![]()
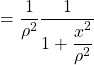 avec
avec ![]()
![]()
![]()
8.a ![]() conviennent.
conviennent.
8.b.![]() est une fonction paire donc, par le même raisonnement qu’à la question 7.b,
est une fonction paire donc, par le même raisonnement qu’à la question 7.b,![]()
8.c. ![]() D’après les égalités des questions 7.b et 8.b, il suffit d’établir l’inégalité demandée pour
D’après les égalités des questions 7.b et 8.b, il suffit d’établir l’inégalité demandée pour ![]() .
.
On constate le résultat suivant : ![]() donc
donc ![]()
![]() Le résultat admis par l’énoncé s’applique à la fonction
Le résultat admis par l’énoncé s’applique à la fonction ![]() , avec
, avec ![]() et
et ![]() ;
; ![]() est donc de classe
est donc de classe ![]() sur
sur ![]() , et
, et
![]()
![]()
Par inégalité triangulaire sur les séries absolument convergentes :
![]()
![]()
![]() D’autre part, pour
D’autre part, pour ![]() ,
,
![]()
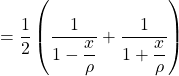
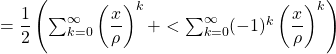
![]()
![]()
donc ![]() est de classe
est de classe ![]() sur
sur ![]() , et
, et ![]()
![]()
d’où :
![]()
![]()
On en déduit bien :
![]()
![]()
ce résultat étant valable, par parité, dans ![]() .
.
8.d. Une récurrence immédiate sur ![]() montre que :
montre que :
![]()
![]()
donc ![]()
![]()
8.e. Lorsque ![]() , et
, et ![]() , un dessin plaçant sur l’axe des réels les nombres suivants :
, un dessin plaçant sur l’axe des réels les nombres suivants : ![]() permet d’observer les inégalités suivantes :
permet d’observer les inégalités suivantes :
![]()
![]() donc
donc ![]() , d’où
, d’où ![]()
![]() ;
;
![]()
![]() donc
donc ![]() , d’où
, d’où ![]()
![]() ;
;
ainsi ![]()
![]()
9.a Là encore un dessin est recommandé, en remarquant que les ![]() forment une subdivision régulière de
forment une subdivision régulière de ![]() .
.
![]() Puisque
Puisque ![]() , on a :
, on a :
![]()
![]()
![]()
![]() Puisque
Puisque ![]() , on a :
, on a :
![]()
![]()
![]()
![]() Par conséquent,
Par conséquent,
![]()
![]()
![]()
![]()
![]()
![]() Il reste à montrer que, pour
Il reste à montrer que, pour ![]() ,
,![]()
![]() , ce qui équivaut à :
, ce qui équivaut à : ![]()
On peut démontrer par récurrence sur ![]() la propriété
la propriété ![]()
![]() est vraie car
est vraie car ![]() .
.
Si ![]() est vraie : pour
est vraie : pour ![]() , on a bien
, on a bien ![]() ; pour
; pour ![]() , ona bien
, ona bien ![]() ; et pour
; et pour ![]() , la formule du triangle de Pascal donne :
, la formule du triangle de Pascal donne :
![]()
![]() par hypothèse de récurrence;
par hypothèse de récurrence;
Ainsi, on obtient bien :
![]()
![]()
9.b. D’après la formule de Stirling, ![]() ; ainsi,
; ainsi,
![]()
![]()
Puisque ![]() , il existe un rang
, il existe un rang ![]() tel que, pour tout
tel que, pour tout ![]() ,
, ![]() ; on a alors :
; on a alors :
![]()
![]()
9.c. ![]() D’après la question 6.d,
D’après la question 6.d, ![]()
![]() .
.
![]() D’après la question 8.d, pour
D’après la question 8.d, pour ![]() ,
, ![]() .
.
![]() D’après la question 9.b, il existe un rang
D’après la question 9.b, il existe un rang ![]() à partir duquel :
à partir duquel : ![]() .
.
Il s’ensuit :
![]()
![]()
![]()
soit ![]()
![]()
Une condition suffisante pour que ![]() est que la suite géométrique figurant dans la majoration soit de raison strictement inférieure à 1, soit :
est que la suite géométrique figurant dans la majoration soit de raison strictement inférieure à 1, soit :
![]()
![]()
![]()
10.a La fonction ![]() est de classe
est de classe ![]() sur le segment
sur le segment ![]() ; nous pouvons donc effectuer une intégration par parties avec
; nous pouvons donc effectuer une intégration par parties avec ![]() ,
, ![]() et
et ![]() .
.
![]()
![]()
![]()
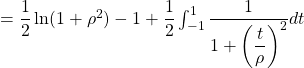
![]() par le changement de variable affine
par le changement de variable affine ![]()
![]()
![]()
Remarque : pour être cohérent avec la question 11, on peut remarquer que ![]() , et que donc :
, et que donc :
![]()
10.b. ![]() La fonction
La fonction ![]() est continue sur
est continue sur ![]() .
.
![]() Elle est strictement croissante sur cet intervalle, car elle est de classe
Elle est strictement croissante sur cet intervalle, car elle est de classe ![]() et
et ![]()

![]()
![]()
![]() , donc
, donc ![]() .
.
![]()
![]() , donc
, donc ![]() et
et ![]() .
.
![]()
![]() réalise donc une bijection strictement croissante de
réalise donc une bijection strictement croissante de ![]() sur
sur ![]() .
.
10.c. ![]() donc
donc ![]() ;
; ![]() admet donc un unique antécédent
admet donc un unique antécédent ![]() par
par ![]() dans
dans ![]() .
.
De plus, ![]()
![]()
![]() , donc
, donc ![]() d’où, par croissance stricte de
d’où, par croissance stricte de ![]() ,
, ![]()
10.d. ![]()
![]() n’ayant que des racines réelles,
n’ayant que des racines réelles, ![]() donc
donc ![]() et
et ![]() est bien défini.
est bien défini.
![]()
![]()
![]()
![]()
![]()
![]() et
et ![]() étant des réels,
étant des réels,
![]()
![]()
![]()
donc ![]()
![]()
Nous reconnaissons une somme de Riemann,
- pour la fonction continue
 ;
; - associée à la subdivision
 , de pas
, de pas  sur le segment
sur le segment ![Rendered by QuickLaTeX.com [-1,1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2045%2018%22%3E%3C/svg%3E) ;
;
donc ![]()
![]()
11.a ![]() La fonction
La fonction ![]() du programme correspond à la fonction
du programme correspond à la fonction ![]() de la question 10).
de la question 10).
![]()
![]() d’après la question 10.c.
d’après la question 10.c.
![]()
![]() car : d’une part
car : d’une part
![]()
![]()
![]()
![]()
![]()
d’autre part :
![]()
![]()
![]()
![]()
![]() Le programme met en oeuvre la méthode de dichotomie, pour la fonction continue
Le programme met en oeuvre la méthode de dichotomie, pour la fonction continue ![]() , sur l’intervalle
, sur l’intervalle ![]() où
où ![]() possède une unique racine d’après le théorème de la bijection et les signes de
possède une unique racine d’après le théorème de la bijection et les signes de ![]() et
et ![]() ). Cette méthode converge vers la racine, donc
). Cette méthode converge vers la racine, donc ![]() vérifie l’équation :
vérifie l’équation : ![]() .
.
11.b. ![]() et
et ![]() ;
; ![]() est strictement croissante, donc
est strictement croissante, donc ![]() .
.
12.a Pour tout ![]() ,
, ![]()
![]()
![]()
![]()
donc ![]() est racine de
est racine de ![]() .
.
Par conséquent ![]() divise
divise ![]() .
.
12.b. Pour tout ![]() ,
, ![]() (faites un dessin), donc
(faites un dessin), donc
![]()
![]()
![]() par définition de
par définition de ![]()
![]()
![]() par parité de
par parité de ![]()
![]()
Ainsi les polynômes ![]() et
et ![]() prennent la même valeur en
prennent la même valeur en ![]() points distincts ; comme ils sont de degré
points distincts ; comme ils sont de degré ![]() ,
,
![]()
![]()
12.c. ![]()
![]()
![]()
![]()
donc ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() par la formule de Stirling.
par la formule de Stirling.
![]()
donc ![]()
12.d. ![]()
![]()
![]()
![]()
![]()
![]()
13.a ![]()
![]()
![]()
![]()
![]() d’après la question 12.b
d’après la question 12.b
![]() par changement d’indice
par changement d’indice ![]()
![]() car n+1 est pair}
car n+1 est pair}
![]()
donc ![]() est un réel, non nul d’après la question 10.d.
est un réel, non nul d’après la question 10.d.
![]()
![]() est de degré inférieur ou égal à
est de degré inférieur ou égal à ![]() , mais
, mais ![]() est pair d’après la question 12.b ; or
est pair d’après la question 12.b ; or ![]() est impair, donc
est impair, donc ![]() ne peut pas comporter de monôme de degré
ne peut pas comporter de monôme de degré ![]() ; ainsi,
; ainsi, ![]() est de degré inférieur ou égal à
est de degré inférieur ou égal à ![]() , donc
, donc ![]() est de degré inférieur ou égal à
est de degré inférieur ou égal à ![]() .
.
![]()
![]() divise
divise ![]() d’après la question 12.a, et
d’après la question 12.a, et ![]() est de degré
est de degré ![]() , donc il existe un réel
, donc il existe un réel ![]() tel que :
tel que :
![]()
![]()
![]() , donc
, donc ![]() , donc :
, donc :
![]()
13.b. Pour tout ![]() ,
,
![]()
![]()
![]()
![]()
14.a ![]() D’après 13)b),
D’après 13)b), ![]()
![]() .
.
![]() D’après 12)d),
D’après 12)d), ![]()
![]() .
.
![]()
![]() et
et ![]() est continue en 1, donc
est continue en 1, donc ![]()
![]()
![]() .
.
Ainsi, ![]()
![]() donc
donc
![]()
![]()
Or ![]() et
et ![]() est strictement croissante, donc
est strictement croissante, donc ![]() (question 10), donc
(question 10), donc
![]() et
et
![]()
14.b. Enfin ![]() , donc
, donc ![]()
![]() , donc :
, donc :
![]()

