Mon parcours pour réussir en maths
J'aprends le cours par coeur
Je travaille avec un prof de maths
Je travaille entre chaque séance
Avis Google France
★★★★★ 4,8 sur 5
Fonctions affines en seconde : exercices
Résumé de cours Exercices et corrigés
Cours en ligne de Seconde Générale
Ces exercices de fonctions affines seconde permettent aux élèves de s’assurer d’avoir bien compris le cours en ligne de maths de seconde et d’être capable de le mettre en application.
D’autres exercices présents sur notre site permettent aux élèves de s’entraîner sur d’autres chapitres : exercices d’arithmétique, exercices sur les variations de fonction, etc..
Exercice fonction affine n°1
Dans chacun des cas suivant, déterminer l’expression de la fonction affine ![]() :
:
1. L’image par ![]() de
de ![]() est
est ![]() et
et ![]() a pour antécédent
a pour antécédent ![]() .
.
2. La droite représentative de ![]() passe par les points
passe par les points ![]() et
et ![]() .
.
3. La droite représentative de ![]() a pour coefficient directeur
a pour coefficient directeur ![]() et
et ![]() .
.
4. ![]() et
et ![]() .
.
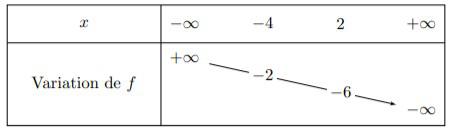
5. La fonction ![]() a pour tableau de variation :
a pour tableau de variation :
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice fonction affine n°2
Soit ![]() une fonction affine définie sur
une fonction affine définie sur ![]() de la forme
de la forme ![]() avec
avec ![]() . On suppose que tous réels
. On suppose que tous réels ![]() et
et ![]() tels que
tels que ![]() (*).
(*).
1. Étudier les variations de ![]() sur
sur ![]() .
.
2. Donner une fonction affine qui satisfait (*). Démontrer que votre fonction satisfait (*).
Exercice fonction affine n°3
On considère une fonction affine ![]() de la forme
de la forme ![]() avec
avec ![]() .
.
On donne le script en Python suivant:

Qu’affiche cette fonction pour ![]() ? m=2?
? m=2?
Correction de l’exercice 1 sur la fonction affine
1. ![]() et
et ![]()
![]() et
et ![]() .
.
Cette équivalence permet d’obtenir le système d’équations à deux inconnues (![]() et
et ![]() ) suivant:
) suivant:
![]()
Par soustraction, on obtient ![]() . Ce qui donne
. Ce qui donne ![]() .
.
Par substitution, en remplaçant la valeur de ![]() dans la première équation, on obtient
dans la première équation, on obtient ![]() .
.
Ce qui donne ![]() .
.
Par conséquent, pour tout réel ![]() ,
, ![]() .
.
2. La droite représentative de ![]() passe par les points
passe par les points ![]() et
et ![]() , alors
, alors ![]() et
et ![]() . Ce qui donne le système d’équations linéaires :
. Ce qui donne le système d’équations linéaires :
![]()
Par soustraction, on obtient ![]() .
.
Donc, ![]() .
.
Par substitution, en remplaçant la valeur de ![]() dans la première équation, on a
dans la première équation, on a ![]() .
.
Ce qui donne ![]() .
.
Par conséquent, pour tout réel ![]() ,
, ![]() .
.
3. Sous la forme ![]() , le réel
, le réel ![]() correspond au coefficient directeur de la droite représentative de
correspond au coefficient directeur de la droite représentative de ![]() alors que
alors que ![]() correspond à l’ordonnée à l’origine de cette droite.
correspond à l’ordonnée à l’origine de cette droite.
Ainsi ![]() .
.
Comme ![]() alors
alors ![]() .
.
Ce qui donne ![]() .
.
Par conséquent, pour tout réel ![]() ,
, ![]() .
.
4. On a ![]() et
et ![]() , alors
, alors ![]() donne l’équation
donne l’équation ![]() .
.
Donc, ![]() .
.
Comme ![]() alors
alors ![]() . Ce qui donne
. Ce qui donne ![]() .
.
Par conséquent, pour tout réel ![]() ,
, ![]() .
.
5. Par lecture du tableau de variation de ![]() , on a :
, on a :
![]() et
et ![]() qui sont équivalentes à
qui sont équivalentes à ![]() et
et ![]() .
.
Cette équivalence permet d’obtenir le système d’équations à deux inconnues:
![]()
Par soustraction, on obtient ![]() .
.
Donc, ![]() .
.
Par substitution, en remplaçant la valeur de ![]() dans la première équation, on a
dans la première équation, on a
![]() . Ce qui donne
. Ce qui donne ![]() .
.
Par conséquent, pour tout réel ![]() ,
, ![]() .
.
Correction de l’exercice 2 sur la fonction affine
1. Par hypothèse de l’énoncé, pour tous réels ![]() et
et ![]() ,
, ![]() implique
implique ![]() . C’est-à-dire que la fonction
. C’est-à-dire que la fonction ![]() inverse l’ordre sur
inverse l’ordre sur ![]() . Donc, elle est strictement décroissante sur
. Donc, elle est strictement décroissante sur ![]() .
.
2. On peut prendre la fonction ![]() définie pour tout réel
définie pour tout réel ![]() par
par ![]() . On veut montrer que
. On veut montrer que ![]() est strictement décroissante sur
est strictement décroissante sur ![]() . Soient
. Soient ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() .
.
![]() Par multiplication par un nombre négatif,
Par multiplication par un nombre négatif, ![]()
![]() Par addition par 1,
Par addition par 1, ![]()
Donc, la fonction ![]() vérifie pour tous réels
vérifie pour tous réels ![]() ,
, ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice 3 sur la fonction affine
![]() Pour
Pour ![]() , cette fonction affiche :
, cette fonction affiche :
La fonction ![]() ,
, ![]() est décroissante
est décroissante
![]() Pour
Pour ![]() , cette fonction affiche :
, cette fonction affiche :
La fonction ![]() ,
, ![]() est croissante
est croissante
Les autres exercices du chapitre fonction affine en seconde se trouvent sur l’application mobile PrepApp.
Retrouvez d’autres cours en ligne de maths seconde sur notre site :

