Qu'est-ce que l'algèbre en mathématiques ?
Analyse complète de l'algèbre en mathématiques

Cours particuliers
Cours particuliers de maths
Quand on travaille les mathématiques au collège, au lycée puis en classe préparatoire on entend souvent parler de l’algèbre. Cette branche des mathématiques est souvent étudiée par les élèves et étudiants sans qu’ils ne sachent réellement ce que signifie le mot algèbre. L’algèbre est utilisée tout au long des années scolaires dans des chapitres comme : la résolution d’équation simple jusqu’aux études de vecteurs et de matrices et de fonctions polynomiales.
Ces chapitres de mathématiques ont tous un point commun, ils utilisent des objets pour définir les variables inconnues d’une équation. Ces objets sont généralement notés comme des lettres, ce fameux “x” qui effraie les élèves quand ils le voient pour la première fois dans une équation. En réalité, l’algèbre n’est pas si compliquée qu’elle n’y paraît. Dans cet article, nous vous détaillons les tenants et aboutissants de ce qu’est l’algèbre.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Quelle est l’histoire de l’algèbre ?
L’algèbre est une des branches connue de l’histoire des mathématiques, avec l’analyse, les probabilités, la géométrie ou encore la trigonométrie. Plusieurs civilisations s’y sont essayées, jusqu’à ce qu’un savant perse, nommé Muhammad ibn Musa al-Khwarizimi (790-850) mette un mot sur cette discipline “l’al jabr”.
La première civilisation à avoir utilisé l’algèbre remonte à deux millénaires avant notre ère. Les premières traces d’équation avec des valeurs inconnues remontent à la civilisation égyptienne et babylonienne. En effet, certains scribes de ces civilisations avaient mis en place des procédures pour résoudre des équations et trouver une quantité inconnue.
Parmi les traces mathématiques retrouvées de cette époque, on a le Papyrus Rhind. Écrit par Ahmès vers 2000 avant J-C, ce papyrus contient 87 problèmes de géométrie, d’algèbre, d’arpentage et d’arithmétique. On peut y retrouver des problèmes d’algèbre traitant de fonction de premier et de second degré.
Exemple : le problème numéro 24 du papyrus de Rhind est le suivant :
“Un nombre ajouté à son septième donne 19, quel est ce nombre ?”. Ce n’est pas très clair, n’est-ce pas ? Cela est dû au fait qu’il n’utilisait pas encore l’algèbre à cette époque. De nos jours, nous pouvons traduire le problème suivant par :
“Voici l’équation à résoudre : x + x/7 = 19. Quelle est la valeur de x ?”
En résolvant l’équation, on obtient 8x/7 = 19 et donc x = 133/8.
Même si l’on ne peut pas considérer que ces premiers problèmes relèvent de l’algèbre, ils s’en rapprochent fortement.
Presque 3 000 ans après le papyrus Rhind, un des plus grands mathématiciens du monde, Al Khwarizmi, exposa les règles de ce qu’on appelle aujourd’hui “l’algèbre”. Ces écrits en arabe sur l’algèbre ont permis à l’Occident de les traduire et d’importer ces connaissances au sein de l’Europe. En plus de l’algèbre, Al Khwarizmi a permis l’importation des chiffres arabes grâce à son ouvrage Traité du système de numération des Indiens.
Les règles à connaître sur l’algèbre
La notation particulière de l’algèbre
L’algèbre utilise des opérations élémentaires comme les additions, les soustractions ou les divisions. Cependant, la particularité de l’algèbre est d’utiliser des lettres pour désigner des variables (pour rappel, les variables peuvent prendre n’importe quelle valeur dans leur ensemble). Ainsi, dans les cas les plus communs, on utilisera des lettres pour exprimer ces variables. Les plus rependues sont a, b, x et y. La multiplication se note, soit avec un point au milieu, avec une parenthèse ou rien si une lettre et un chiffre se chevauchent.
On a donc :
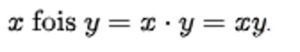
Les règles de propriétés de calcul en algèbre
Même si vos professeurs vous ont répété maintes et maintes fois les priorités pour les calculs algébriques. Il est important de les rappeler : les premiers calculs à effectuer sont ceux situés dans les parenthèses.
Exemple : 3+5*(4-5) = -2
Ensuite on s’occupe des calculs à l’intérieur de crochets.
Exemple : 5 – 6-[(6-3)+(3+8)]
= 5 – 6-[3+11]
= 5-6-14
= -15
Si les parenthèses et les crochets ne vous permettent pas d’identifier les premiers calculs à effectuer, il faut alors commencer par calculer les puissances.
Exemple : 3 + 5*4+3²
= 3 +5*4+9
= 3+20+9
= 32
Les avants derniers calculs à avoir la priorité sont les multiplications et les divisions. Les derniers calculs à effectuer sont les additions et les soustractions.

Comment apprendre facilement l’algèbre ?
La place des maths dans l’enseignement est très importante. Dès la maternelle, les jeunes françaises et français étudient les mathématiques. Pourtant, nous savons à quel point les mathématiques sont difficiles à enseigner pour les professeurs et à comprendre pour les élèves. Les mathématiques suivent des règles qui peuvent paraître déroutantes pour certains. Avec l’introduction de l’algèbre à la fin du collège, les élèves sont souvent étonnés de travailler avec des lettres en mathématiques, ce qui en bloque certains.En conséquence, certains ont tendance à prendre des cours de maths particuliers.
Dans cet article, nous essaierons de vous donner des petits conseils pour comprendre les calculs en algèbre et pour réussir vos évaluations sur ce domaine des mathématiques.
Les conseils de base pour débuter en algèbre
Nous vous présentons ici, une liste non exhaustive de conseils qui vous permettront d’être meilleur en algèbre.
Pour les débutants en algèbre :
- Les opérations simples ne doivent pas vous poser de problème. Vous devez être capable de calculer n’importe quelle opération simple, sans variable.
- Connaître les règles de priorité de calculs : parenthèses, crochets, puissances, multiplication, division et soustraction.
- Il est important d’organiser vos calculs pour ne pas vous perdre. Mettez les calculs prioritaires d’un côté.
Pour les personnes de niveau intermédiaire en algèbre :
- Dites vous que les variables représentées par des lettres, sont des nombres inconnus. Vous pouvez remplacer ces variables par un point d’interrogation au début pour vous familiariser avec ces nouvelles variables.
- N’oubliez pas que vous pouvez simplifier des variables. Pour vous aider, dites-vous que vous ne pouvez additionner ou soustraire deux variables que si elles appartiennent à la même famille.
Par exemple : 2x + 3x = 5x. Mais attention : 2x + 3y ≠ 5xy.
- Résoudre une équation revient à annuler une variable d’un côté ou de l’autre de l’équation. Pour simplifier, vous pouvez vous dire qu’il faut toujours équilibrer l’équation, pour cela il faut connaître les opérations équivalentes. L’addition d’un côté équivaut à une soustraction de l’autre côté. Une multiplication équivaut à une division.
Par exemple : 2x + 3 = 5 équivaut à 2x = 5-3 = 2 et 2x = 2 équivaut à x = 2/2 = 1
Pour l’algèbre d’un niveau avancé, notamment pour les classes préparatoires, vous aurez besoin de plusieurs exercices pour connaître toutes les subtilités de cette branche mathématique. Vous commencerez à étudier les fonctions complexes et les vecteurs et matrices.
Les ressources importantes à utiliser pour être meilleur en algèbre
Au vu de l’importance des mathématiques dans le système français, Groupe Réussite propose de nombreux cours et stages intensifs pour vous préparer à vos futures évaluations, concours ou examens. Pour vous préparer au lycée, de nombreux livres de préparation au baccalauréat peuvent vous aider à réviser les mathématiques, le codage, et l’algèbre.
On peut citer les manuels suivants :
- Spécialité Maths, Objectif Bac Terminale, édité chez Hachette. Ce livre suit le nouveau programme lié à la réforme du bac. En plus de 200 exercices corrigés, ce manuel offre des cours détaillés ainsi que 12 sujets de bac corrigés.
Prix : 10 € sur Momox.
- Prépabac spécialité Mathématiques, édité chez Hatier. 350 exercices corrigés, des cours visuels et des mémos visuels.
Prix : 12,90 €.
- Annabac spécialité Mathématiques, édité chez Hatier.
84 sujets corrigés avec des conseils sur les méthodes à adopter pour réussir son bac.
Prix : 6,99 €.
Pour les étudiants en classe préparatoire, de nombreux manuels existent également en fonction des différentes spécialités suivies. En revanche, compléter ses révisions personnelles avec des cours particuliers ou des participations à des stages intensifs de révision est plus que recommandé au vu de la complexité et de la richesse des programmes en CPGE.