Qu'est-ce que la geométrie en mathématiques ?
La géométrie pour le plaisir, vraiment ?

Cours particuliers
Cours particuliers de maths
Si des mots tels que théorème de Thalès, théorème de Pythagore, droite, segment, carré, losange, cercle… vous disent quelque chose, alors vous avez certainement étudié la géométrie. Il est d’ailleurs quasi certain que vous ayez déjà étudié ces notions, sachant qu’elles sont au programme dans les classes de primaire et de collège. La géométrie est une branche des mathématiques dont le rôle est très important dans l’histoire des mathématiques.
Pourtant, la géométrie, en particulier la géométrie euclidienne, reste relativement accessible, nécessitant évidemment quelques connaissances mathématiques. Il est bien sûr possible d’aller plus loin, en utilisant des outils mathématiques plus complexes et un cours de maths particuliers.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
À quoi sert la géométrie ?
Les règles de géométrie ne sont pas simplement des règles théoriques, elles s’appliquent également dans le monde réel. En effet, les architectes qui dessinent les plans des bâtiments doivent connaître les règles fondamentales de la géométrie. L’architecture commence avec la géométrie. En -20, l’ancien architecte romain Marcus Vitruve rédigea De Architectura dans lequel il pose un certain nombre de règles géométriques à respecter en architecture. En effet, pour Vitruve, «sans symétrie et sans proportion aucun temple ne peut avoir un plan régulier».
L’apprentissage de la géométrie est donc indispensable et pas seulement en raison de l’importance des maths dans le système scolaire. Participer aux stages ou aux cours particuliers proposés par Groupe Réussite peut vous permettre de mettre fin à certains blocages en mathématiques, notamment en géométrie, pour réussir au mieux vos interrogations, examens ou concours, extrêmement utiles pour progresser dans une discipline centrale.
Quelle est l’origine de la géométrie ?
Le mot géométrie provient des termes grecs “gê” (terre) et “métron” (mesure). On peut donc définir la géométrie comme l’étude de l’espace et l’étude des figures de l’espace.
Les Grecs occupent une place centrale dans l’histoire de la géométrie. Ils occupent cette place grâce à certains des plus grands mathématiciens du monde tels Pythagore, Thalès ou encore Euclide. S’il y a bien des précurseurs aux Grecs dans le domaine de la géométrie, Michel Serres dans Les origines de la géométrie, montre que les Grecs ont véritablement fondé cette science, bien que les Égyptiens, Babyloniens ou Chinois connaissaient certaines règles géométriques avant eux. La connaissance des règles de la pyramide en géométrie a été indispensable à la construction des pyramides d’Égypte.
La géométrie euclidienne: aux fondements de la géométrie
Les origines de la géométrie euclidienne
La géométrie connaît plusieurs ramifications, même si la branche fondatrice est la géométrie classique qui comprend principalement la géométrie euclidienne. D’ailleurs, on emploie très souvent le terme de géométrie pour désigner la géométrie classique.
La géométrie euclidienne a véritablement fondé la géométrie moderne. Euclide a développé une science étudiant les figures du plan et de l’espace, comme le triangle, le rectangle ou alors le cercle.
Cette géométrie est étudiée en premier dans les programmes scolaires, car elle pose les bases de la géométrie. De plus, elle ne nécessite pas de connaissances mathématiques extrêmement poussées. En revanche, avec la trigonométrie, il est possible d’aller plus loin et d’approfondir ses connaissances.
C’est pour ces raisons que la géométrie euclidienne est centrale dans l’enseignement des mathématiques en France.
Les définitions fondamentales en géométrie euclidienne
On peut commencer par définir certaines figures géométriques très courantes
- Droite : objet formé de points alignés, représentée en pratique par une ligne droite
- Segment : portion de droite délimitée par 2 points
- Polygone : figure géométrique fermée
- Quadrilatère : polygone à 4 côtés
- Parallélogramme : polygone dont les côtés opposés sont parallèles
- Losange : parallélogramme dont les 4 côtés sont de même longueur
- Rectangle : parallélogramme dont les 4 angles sont droits (angle de 90°)
- Carré : parallélogramme dont les 4 côtés sont de même longueur et dont les 4 angles sont droits
- Triangle : figure formée par 3 points reliés entre eux par des segments
- Triangle rectangle : triangle dont l’un des angles est droit
- Triangle isocèle : triangle ayant au moins 2 côtés de même longueur
- Triangle équilatéral : triangle ayant tous ses côtés de même longueur
Quelques théorèmes fondamentaux de la géométrie euclidienne
2 théorèmes occupent une place particulière en géométrie : le théorème de Pythagore et le théorème de Thalès.
Le théorème de Pythagore nous dit ceci : Soit un triangle rectangle ABC. Ce triangle a 3 sommets et l’angle droit se trouve au sommet B.
Alors on a :
(AB)² + (BC)² = (AC)² (AB = distance entre A et B)
Ce théorème nous permet de déterminer la distance entre 2 sommets si les 2 autres longueurs sont connues.
En posant AB = a, BC = b et AC = c, on a :
a² + b² = c²
Dès lors, si on sait par exemple que AB = 4 cm = a et que BC = 3 cm = b, on a :
c² = 4² + 3² = 16 + 9 = 25
Pour déterminer c = AC, on fait :
racine(c²) = c = racine(25) = 5 (c est positif)
Donc AC = 5 cm
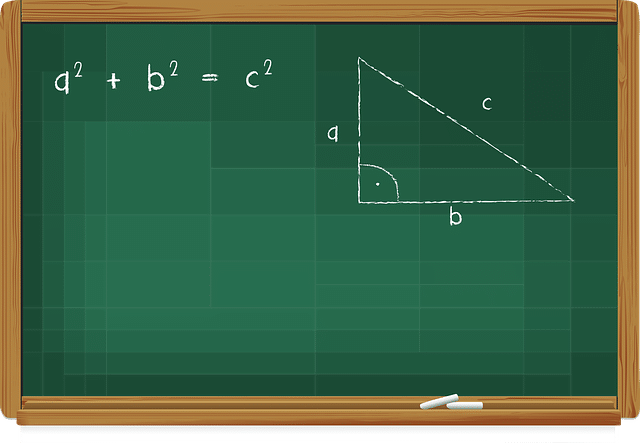
Quant au théorème de Thalès, il nous dit que si on a un triangle ABC et 2 points M et N, tels que M est un point du segment AB et N un point du segment AC et que si MN est parallèle à BC alors :
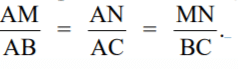
Pour aller plus loin: les autres branches de la géométrie
La géométrie euclidienne permet de poser des fondements. Toutefois, d’autres développements eurent lieu dans l’histoire enrichissant les connaissances en géométrie. Les mathématiciens dans le monde arabe développent en premier la géométrie algébrique à partir du XIe siècle, repris ensuite par Descartes. La géométrie algébrique utilise les outils de l’algèbre, afin de résoudre des problèmes géométriques complexes.
La géométrie différentielle étudie principalement les courbes et les surfaces. Toutefois, la géométrie n’est pas qu’une discipline théorique. En effet, elle a de nombreuses applications, qui parfois même ne nécessitent pas de connaissances mathématiques poussées. C’est le cas de la géométrie descriptive.
L’objectif de la géométrie descriptive est de dessiner des objets selon un angle de vue précis ou chercher à résoudre des problèmes d’intersection entre des surfaces. La géométrie est bien une science présente au quotidien. La connaissance de ces règles est une nécessité pour notre monde.
Vous pouvez aussi découvrir l’article « Qu’est-ce que le codage ? » pour mieux comprendre en quoi consiste le codage et quelles utilités il a aujourd’hui.

