Qu'est-ce que la trigonométrie en mathématiques ?
Découvrir les règles trigonométriques en mathématiques

Cours particuliers
Cours particuliers de maths
La trigonométrie est souvent perçue, à tort ou à raison, comme difficile. De nouvelles fonctions aux noms intrigants, sinus, cosinus ou tangente notamment, sont introduites. Qu’en est-il réellement ?
Découvrez les professeurs de maths particuliers chez Groupe Réussite pour comprendre et appliquer les règles trigonométriques et réussir en maths.
Quelle est l’histoire de la trigonométrie ?
Le mot trigonométrie est issu des termes grecs trigonos (triangle, triangulaire) et métron (mesure). La trigonométrie est donc une discipline mesurant différents éléments remarquables du triangle, comme les angles ou les côtés. On trouve des traces de la trigonométrie dans les civilisations égyptiennes, babyloniennes. La fonction sinus est utilisée pour la première fois dans les Sulba-Sutras, écrites entre le VIIIe et le Ve siècle avant J-C. Il s’agit de textes posant les premières règles mathématiques.
L’objectif de la trigonométrie à ses débuts était de résoudre des problèmes pratiques. Ainsi, les fonctions trigonométriques ont été créées pour aider les astronomes ou les marins. En effet, la mesure des angles et des côtés d’un triangle s’avère nécessaire pour estimer, par exemple, la distance restante pour arriver au port.

Comme souvent dans l’histoire des mathématiques, les Grecs vont synthétiser et enrichir les savoirs sur la trigonométrie. Les plus grands mathématiciens au monde vont y jouer un rôle. Le mathématicien Hipparque de Nicée fut le premier à utiliser des tables trigonométriques. Grâce à celles-ci, il réussit à estimer la distance entre le Soleil et la Lune et leurs tailles.
Ptolémée d’Alexandrie les redécouvre et les publie vers le IIe siècle après J-C. Il les utilise pour calculer la trajectoire des planètes. Toutefois, il ne croit pas à l’héliocentrisme (l’idée que la Terre tourne autour du Soleil), au contraire de Pythagore. Cette “erreur” fausse en grande partie ses calculs.
Après la période grecque, ce fut principalement en Orient que la trigonométrie se développa. Ce sont des mathématiciens arabes tels Abu-I-Wafa ou Omar Khayyam qui émancipent la trigonométrie de l’astronomie en instituant des formules de trigonométrie comparables aux nôtres.
La trigonométrie est redécouverte en Europe, surtout à partir de la Renaissance, avec des mathématiciens comme Adrien Romain qui introduit la notation sin ou Bartholomäus Pitiscus qui publie un ouvrage sur la trigonométrie intitulé Trigonometria en 1595, donnant ainsi son nom à la discipline.
Comment peut-on définir la trigonométrie ?
La trigonométrie est une branche des mathématiques, tout comme l’algèbre, l’analyse ou encore les probabilités. Il s’agit d’un champ des mathématiques qui fait le lien entre la mesure des angles des triangles rectangles et la longueur de leurs côtés. La trigonométrie est donc intimement liée à la géométrie.
La trigonométrie a pour objectif de simplifier la résolution de problèmes géométriques. En effet, l’utilisation de formules trigonométriques permet de :
- Calculer la longueur d’un côté d’un triangle rectangle lorsqu’on connaît la longueur d’un côté et les mesures d’au moins 2 angles.
- Calculer les mesures des 2 autres angles que l’angle droit d’un triangle rectangle en connaissant les longueurs d’au moins 2 côtés.
Pour cela, on utilise des fonctions trigonométriques. Les principales sont la fonction cosinus (ou cos), la fonction sinus (ou sin) et la fonction tangente (ou tan).
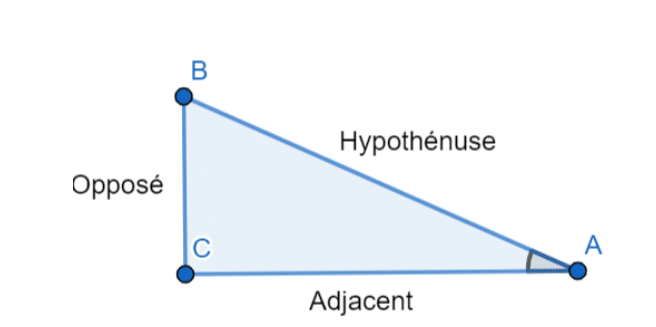
Soit ABC un triangle rectangle en C,
On a alors

Pour se souvenir de ces formules, on peut retenir ceci.
SOH CAH TOA (Sinus Opposé Hypoténuse, Cosinus Adjacent Hypoténuse, Tangente Opposé Adjacent).
Les formules générales de trigonométrie
Les fonctions trigonométriques peuvent être utilisées en mathématiques. Il est donc possible de dériver ou d’intégrer des fonctions trigonométriques. Dans ce cas, il s’avère nécessaire d’utiliser les radians, seule la valeur en radian ayant un sens mathématique.
On peut utiliser ce tableau de conversion pour obtenir la valeur en radian d’une valeur en degré.

Quelques formules utiles en trigonométrie, valables pour n’importe quel a, b et x :
- cos²(x)+sin²(x) = 1
- cos(a + b) = cos(a)
- cos(b) − sin(a) sin(b)
- sin(a + b) = sin(a) cos(b) + cos(a) sin(b)
- tan(x) = sin(x)/cos(x)
- cos(x + 2π) = cos(x)
- sin(x + 2π) = sin(x)
- tan(x + π) = tan(x)
- cos(2x) = 2cos²(x)-1
- sin(2x) = 2sin(x)cos(x)
On peut retenir les dérivées des fonctions sinus, cosinus pour n’importe quel x :
- cos’(x) = -sin(x)
- sin’(x) = cos(x)
On a aussi la dérivée de la fonction tangente pour x qui n’est pas sous la forme π/2+kπ, k étant un entier relatif :
- tan’(x) = 1/cos²(x)
Utiliser ces fonctions dans la résolution de problèmes géométriques
On peut utiliser les fonctions trigonométriques pour mesurer le degré d’un angle ou pour calculer la longueur d’un côté.
Comment trouver une longueur avec la trigonométrie ?
Exemple d’un exercice sur la trigonométrie.
Soit le même triangle qu’au-dessus ABC rectangle en C.
On pose AC = 5 cm et l’angle A est de degré 25 et est noté â.
On cherche une valeur approchée de AB.
Dans cette situation, le triangle est rectangle en C. On peut donc utiliser les formules trigonométriques.
Ici, on cherche une valeur de AB.

Comment trouver la valeur d’un angle avec la trigonométrie ?
Soit le même triangle ABC rectangle en C.
On pose AC = 5 cm et BC = 2 cm (on ne s’occupe pas de AB).
On souhaite calculer l’angle de B.
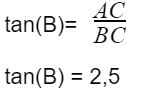
Pour trouver la valeur de l’angle B, on utilise la touche tan-1 sur la calculatrice pour 2,5.
On trouve alors un angle d’environ 68°.
Importance de la trigonométrie à l’école
La trigonométrie est abordée pour la première fois en classe de Troisième. En Troisième, on utilise la trigonométrie surtout pour calculer le degré des angles ou la longueur d’un des côtés. Les exercices sur la trigonométrie portent principalement sur la résolution de problèmes géométriques. En Seconde, l’introduction de la notion du cercle trigonométrique permet d’utiliser plus largement cette dernière.
En particulier, il permet de calculer très simplement des valeurs remarquables de certains cosinus ou sinus. Ensuite, pour poursuivre l’apprentissage de la trigonométrie, il faut suivre la spécialité mathématiques en Première. À partir de ce moment-là, la trigonométrie n’est plus étudiée exclusivement en lien avec la géométrie. En effet, les élèves apprennent par exemple à dériver ou intégrer des fonctions trigonométriques.
À quoi sert la trigonométrie ?
La trigonométrie a un rôle central dans notre vie quotidienne et pas seulement en raison de l’importance des maths dans le système scolaire et de la place des maths dans l’enseignement. La trigonométrie est utilisée dans de très nombreuses activités, même si les calculs se font en général par ordinateur, par du codage informatique. Comme autrefois, la trigonométrie peut être employée en navigation. En effet, elle permet de calculer la distance dans un triangle et donc la distance séparant un bateau d’un rivage par exemple.
En climatologie ou en sciences économiques, l’étude des périodicités saisonnières nécessite l’emploi des fonctions sinus ou cosinus. Plus étonnant encore, la trigonométrie est aussi présente dans l’univers de la musique. Grâce à la trigonométrie, Pythagore a montré que les sons obtenus en pinçant 2 cordes de longueurs différentes sont d’autant plus harmonieux que les 2 longueurs sont de petits multiples.
Un musicien n’a pas besoin de connaître la trigonométrie. Toutefois, il ne pourra pas comprendre ce point spécifique s’il ne maîtrise pas certaines règles de trigonométrie. La trigonométrie a donc bien sa place dans notre vie et dans de nombreux métiers.

