Chapitres de maths en Terminale S2
Exercices et corrigés sur la fonction exponentielle en Terminale S2
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale S2
Beaucoup d’exercices sont classiques et permettent de progresser sur les fonctions exponentielles en terminale S2. Retrouvez ci-dessous quelques exercices corrigés qui vous seront utiles dans votre préparation du bac S2.
QCM sur la fonction exponentielle en terminale S2
Question 1 :
Soit ![]() la fonction définie sur
la fonction définie sur ![]() par
par
![]() ,
, ![]() sa fonction dérivée et
sa fonction dérivée et ![]() sa primitive s’annulant en 0.
sa primitive s’annulant en 0.
![]()
a. ![]()
b. ![]()
c. n’existe pas
d. aucune des trois propositions ci-dessus n’est correcte.
Question 2 :
![]()
a. ![]()
b. ![]()
c. n’existe pas
d. aucune des trois propositions ci-dessus n’est correcte.
Question 3 :
Le nombre de solution(s) de l’équation ![]() est:
est:
a. 0
b. 1
c. 2
d. aucune des trois propositions ci-dessus n’est correcte.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé du QCM de terminale S2 les fonctions exponentielles
Question 1 :
On sait que, pour tout nombre réel ![]() ,
, ![]()
Donc, pour tout nombre réel ![]() ,
, ![]()
Donc, pour tout nombre réel ![]() ,
, ![]()
Donc, pour tout nombre réel ![]() ,
, ![]()
On sait que ![]() et
et ![]()
Donc par composition ![]()
De plus, ![]()
Donc, par somme, ![]()
On a, pour tout ![]() ,
, ![]() et
et ![]()
Donc ![]()
Question 2 :
On a montré que pour tout nombre réel ![]() ,
, ![]()
On sait que ![]() et
et ![]()
Donc par composition ![]()
De plus, ![]()
Donc, par somme, ![]()
On a, pour tout ![]() ,
, ![]() et
et ![]()
Donc ![]()
Question 3 :
Il ne faut bien sûr pas chercher à résoudre directement l’équation!
On a montré que ![]()
On sait que pour tout nombre réel ![]() ,
, ![]()
Donc pour tout nombre réel ![]() ,
, ![]()
Donc ![]()
Donc
![]()
![]()
![]()
Soit ![]()
Or, pour tout nombre réel ![]() ,
, ![]() donc
donc ![]() et donc
et donc ![]()
Soit ![]()
Donc, pour tout nombre réel ![]() ,
, ![]()
Donc, pour tout nombre réel ![]() ,
, ![]()
Donc la fonction ![]() est strictement décroissante sur
est strictement décroissante sur ![]() .
.
De plus, la fonction ![]() est continue sur
est continue sur ![]() ( somme de fonctions continues sur
( somme de fonctions continues sur ![]() )
)
Enfin, on a montré que ![]() et
et ![]()
Donc, d’après le théorème des valeurs intermédiaires, l’équation ![]() admet une unique solution sur
admet une unique solution sur ![]() .
.
Exercices sur les fonctions exponentielles terminale S2
Exercice calculer une limite en terminale S2
Calculer ![]()
Exercice sur la dérivation
Dériver la fonction f définie sur R par ![]() =
=![]()
Corrigé des exercices sur les fonctions logarithme
Corrigé de l’exercice sur le calcul d’une limite
Solution:
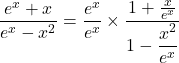
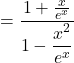
Or ![]() =
=![]() =
=![]()
donc
![]() =
=![]() =
=![]()
Donc 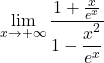 =
=![]()
d’où ![]()
Exercice sur la dérivation terminale S2
Solution:
f est de la forme ![]() avec u=4x+3 et u’=4
avec u=4x+3 et u’=4
Donc f'(x)= ![]() =
=![]()
La fonction ![]() admet donc bien la droite
admet donc bien la droite ![]() d’équation
d’équation ![]() pour asymptote en
pour asymptote en ![]() .
.
Retrouvez d’autres exercices et corrigés des cours de maths niveau terminale S2 :
- Exercices révision en terminale S2: Limites, continuité et dérivabilité
- Exercices pour progresser en terminale S2 : Primitives et calcul intégral
- Exercices corrigées pour réussir sur la fonction logarithme népérien en terminale S2
- Progresser avec les exercices sur les équations différentielles

