Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Avis Google France
★★★★★ 4,8 sur 5

Généralités sur les fonctions en seconde générale: exercices

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Seconde Générale

Entraînez-vous avec les exercices corrigés sur les généralités et les fonctions pour réussir en maths seconde.

Généralité sur les fonctions : exercice n°1

Le tableau suivant donne les coordonnées des points appartenant à la courbe représentative d’une fonction $f$ définie sur $[-1;4]$ .

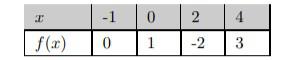
1. Donner l’image par $f$ de $2$ .

2. Peut-t-on calculer l’image par $f$ de $2,5$ ? Justifier.

Exercice n°2 : tableau de valeur de la fonction

Soit $f$ la fonction définie pour tout réel $x$ par $f(x)=\dfrac{2x}{x^2+1}$ .

1. Compléter le tableau de valeur de la fonction $f$ suivant:

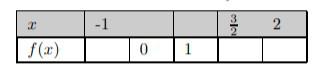
2. Résoudre algébriquement l’inéquation $f(x)>0$ et $f(x)\leq -1$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Exercices n°3 : échelle de quantité

Le graphique suivant montre le nuage de points sur vingt semaines des ventes d’un commerçant. L’échelle de la quantité vendue est de $10^4$ .

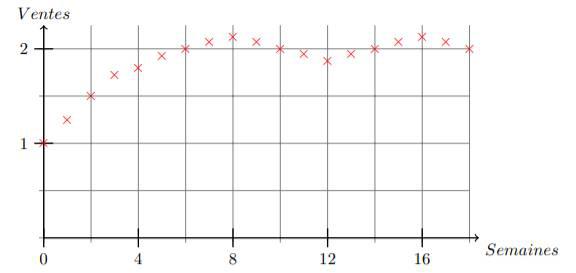
1. Donner les quantités vendues pour les semaines $8$ , $12$ et $15$ . Les résultats attendus sont approximatifs.

2. Quelles sont les semaines où la quantité des ventes est de $20\ 000$ ?

3. Quelles sont les semaines où les ventes dépassent strictement $20\ 000$ ?

4. Quelles sont les semaines où les ventes sont inférieures à $15\ 000$ ?

5. On note $f$ la fonction définie sur $[0;19]$ et qui passe par les points définis sur le graphique ci-dessus.

On note $\mathscr{C}_f$ la courbe représentative de la fonction $f$ dans un repère orthonormé.

a) Donner l’image par $f$ de $8$ et celle de $12$ . Calculer $f(15)$ .

b) Donner les antécédents par $f$ de 20 000.

c) Résoudre l’équation $f(x)=$ 15 000.

d) Résoudre l’inéquation $f(x)<$ 20000 puis l’inéquation $f(x)\geq 15\ 000$ . Donner les résultats sous forme d’inégalités.

Généralités sur les fonctions : correction de l’exercice 1

1 – L’image par $f$ de $2$ est $-2$ .

2 – Oui, on peut calculer l’image par $f$ de $2,5$ car $x=2,5$ appartient à l’intervalle $[-1;4]$ , l’ensemble de définition de $f$ .

Correction de l’exercice 2 : tableau de valeur de la fonction

1 – En remplaçant $x$ par la valeur indiquée dans la parenthèse de la variable de la fonction :

$f(-1) = \dfrac{2(-1)}{(-1)^2+1}$

$f(-1) = -1$

$f(x) = 0$ est équivalent à $2x=0$ (car une fraction est nulle si et seulement si son numérateur est nul).

$f(x) = 1$ est équivalent à $\dfrac{2x}{x^2+1}=1$

$f(x) = 1$ est équivalent à $2x=x^2+1$

$f(x) = 1$ est équivalent à $x^2-2x+1=0$

$f(x) = 1$ est équivalent à $(x-1)^{2}=0$ .

Par conséquent, $f(x)=1$ si et seulement si $x=1$ .

$\bullet$ En remplaçant $x$ par $\dfrac{3}{2}$ , on obtient:

$f(\dfrac{3}{2})= \dfrac{2(\frac{3}{2})}{(\frac{3}{2})^2+1}$

$f(\dfrac{3}{2}) = \dfrac{3}{\frac{9}{4}+1}$

$f(\dfrac{3}{2}) = \dfrac{12}{13}$

$\bullet$ En remplaçant $x$ par $2$ , on obtient $f(2) = \dfrac{2(2)}{(2)^2+1} =\dfrac{4}{5}$

Il ne reste plus qu’à remplir le tableau avec les résultats obtenus.

2 – D’une manière générale, pour résoudre algébriquement une inéquation, il faut mettre toutes les expressions d’un côté et $0$ de l’autre.

$\bullet$ Pour tout $x\in \mathbb{R}$ , $x^2+1>0$ . Donc, $f(x)$ est du signe de $2x$ . Alors, $f(x)>0 \Leftrightarrow x>0$ .

Par conséquent, $f(x)>0 \Leftrightarrow x\in ]0;+\infty[$ .

$\bullet$ $f(x)\leq -1\Leftrightarrow \dfrac{2x}{x^2+1}+1\leq 0$ . Ce qui donne l’équivalence :

$f(x) \leq -1 \Longleftrightarrow \dfrac{x^2+2x+1}{x^2+1} \leq 0$

$f(x)\leq -1 \Longleftrightarrow \dfrac{(x+1)^2}{x^2+1}\leq 0$

Comme pour tout réel $x$ , $x^2+1>0$ , alors $f(x)\leq -1 \Leftrightarrow (x+1)^2\leq 0$ .

Le seul cas où cette dernière inégalité est vraie est $x=-1$ .

Par conséquent, $f(x)\leq -1 \Leftrightarrow x\in \{-1\}$ .

Correction de l’exercice 3 : échelle de quantité

1 – L’échelle sur l’axe des ordonnées est en $10^4$ . Donc, chaque unité sur le graphique correspond à $10\ 000$ quantités vendues.

Par lecture graphique: La quantité vendue :

$\bullet$ pour la semaine $8$ est d’environ $2,2\times 10^4 = 22\ 000$ unités.

$\bullet$ pour la semaine $12$ est d’environ $1,7\times 10^4= 17 \ 000$ unités.

$\bullet$ pour la semaine $15$ est d’environ $2,1\times 10^4= 21 \ 000$ unités.

2 – La quantité des ventes est de $20\ 000$ pour les semaines 6, 10, 14 et 18.

3 – Les ventes dépassent strictement $20\ 000$ pour les semaines 7, 8, 9, 15, 16 et 17.

4 – Les ventes sont inférieures à $15\ 000$ pour les semaines 0, 1 et 2.

5 – a) Dans la première partie, on a seulement quelques points qui ont une image. La fonction $f$ est définie sur $[0;19]$ à valeurs dans $\mathbb{R}$ alors tous les réels entre $0$ et $19$ ont une image par $f$ :

$f: [0;19] \longrightarrow \mathbb{R}$

$x \mapsto f(x)$

Comme dans la question précédente

$\bullet$ L’image de 8 par $f$ est d’environ 22 000 : $f(8)\approx$ 22 000

$\bullet$ L’image de 12 par $f$ est d’environ 17 000 : $f(12)\approx$ 17 000

$\bullet$ L’image de 15 par $f$ est d’environ 15 000 : $f(15)\approx$ 21 000.

b) Les antécédents par $f$ de 20 000 sont 6, 10, 14 et 18 :

$f(6)=f(10)=f(14)=f(18)$

c) Les solutions de l’équation $f(x)=$ 15 000 sont les antécédents de 15 000 par $f$ . Donc cette équation a pour ensemble de solution $\{2\}$ : $f(2)=$ 15 000.

d) Comme la fonction $f$ est définie sur un ensemble de réels, alors la solution d’une inéquation de la forme $f(x)\leq k$ ou $f(x)\geq k$ est un intervalle ou une réunion d’intervalles. Elle peut s’écrire également sous la forme d’inégalités. Par lecture graphique:

$\bullet$ $f(x)<$ 20 000 a pour solution l’ensemble de réels $x$ tels que $0\leq x< 6$ ou $10< x < 14$ .

Sous forme d’intervalle, on peut écrire :

$f(x)<$ 20 000 pour $x\in [0;6[\cup ]10;14[$

$\bullet$ $f(x)\geq$ 15 000 a pour solution l’ensemble de réels $x$ tels que $2\leq x< 19$ . Sous forme d’intervalle, on peut écrire: $f(x) \geq$ 15 000 pour $x\in [2;19[$

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION