Chapitres de maths en Terminale D

Suites en Terminale D : exercices et corrigés

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de maths en Terminale D

Vous trouverez ci-dessous des exercices corrigés gratuits sur les suites pour les élèves préparant le bac D.

1. Suites récurrentes et étude de suites

Exercice 1 :

On considère la suite $(u_{n})$ définie sur $\mathbb{N}$ par :

$\left \{ \begin{array}{c @{=} c} u_{0} = 2 \\ u_{n+1} = 2u_{n}-3 \\ \end{array} \right.$

Montrez que $\forall n \in \mathbb{N}\text{, }u_{n}=3-2^{n}$

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Corrigé de l’exercice 1 :

Montrons ceci par récurrence :

Posons la propriété à démontrer : soit $P(n)\text{ : }"u_{n}=3-2^{n}"$ .

Initialisation : $u_{0}=2$ et $3-2^{0}=3-1=2$ , on a donc bien $u_{0}=3-2^{0}$ . $P(0)$ est vraie.

Hérédité : soit $n \in \mathbb{N}$ , supposons que $P(n)$ est vraie. Montrons que $P(n+1)$ est vraie.

$u_{n+1}=2u_{n}-3=2\left(3-2^{n}\right)-3=6-2^{n+1}-3=3-2^{n+}$ . Donc $P(n+1)$ est vraie.

Conclusion :} $\forall n \in \mathbb{N}\text{, }P(n)$ est vraie, c’est-à-dire

$\boxed{\forall n \in \mathbb{N}\text{, }u_{n}=3-2^{n}}$

2 – Vrai / Faux sur la monotonie

Les affirmations suivantes sont-elles vraies ou fausses. Justifiez vos réponses :

Question 1 :

Toute suite décroissante est majorée.

Question 2 :

Toute suite décroissante et minorée par 0 a pour limite 0.

Question 3 :

Toute suite croissante et majorée est bornée

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Corrigé de la question 1 :

Toute suite décroissante est majorée par son premier terme

$\text{Soit }n_{0} \in \mathbb{N}\text{, }\forall n \geq n_{0}\text{, }u_{n+1} \leq u_{n}$

$\Longrightarrow u_{n} \leq u_{n_{0}}$

Corrigé de la question 2 :

Soit $\epsilon >0$ et $\forall n \in \mathbb{N}\text{, }u_{n}=\epsilon + \frac{1}{1+n}$ . La suite $(u_{n})$ est strictement décroissante (car la fonction inverse est strictement décroissante sur $]0,+\infty[$ ) et minorée par $0$ : $\forall n \in \mathbb{N}\text{, }u_{n} > \epsilon > 0$ . Cependant :

$\lim\limits_{n \longrightarrow +\infty} u_{n} = \epsilon >0$

La suite $(u_{n})$ ne peut donc pas converger vers $0$ .

Corrigé de la question 3 :

Toute suite croissante est minorée par son premier terme. Si elle est de plus majorée, elle est donc bien bornée

3 – Limites de suites

Exercice 1 :

Calculer la limite quand $n \rightarrow +\infty$ de la suite suivante $u_{n}=-n^{3}+2n^{2}$

Exercice 2 :

Calculer la limite quand $n \rightarrow +\infty$ de la suite suivante $u_{n}=2+(-0.3)^{n}$ :

Exercice 3 :

Calculer la limite quand $n \rightarrow +\infty$ de la suite suivante $u_{n}=1+\displaystyle{\frac{1}{n}}-\displaystyle{\frac{2}{n^{2}}}$

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Corrigé de l’exercice 1 :

On est en présence d’une forme indéterminée : $-\infty+\infty=F.I$ . Pour lever l’indétermination, il faut factoriser par le terme dominant à l’infini, ici $-n^{3}$

$u_{n}=-n^{3}\left(1-\frac{2}{n}\right)$

$\lim\limits_{n \longrightarrow +\infty} \frac{2}{n} = 0$

Donc par somme et produit :

$\boxed{\lim\limits_{n \longrightarrow +\infty} u_{n}=-\infty}$

Corrigé de l’exercice 2 :

La suite $((-0.3)^{n})$ est une suite géométrique de raison $q=-0.3$ . Comme $|q|<1$ ( $\Longleftrightarrow q \in ]-1,1[$ ), nous pouvons affirmer que $\lim\limits_{n \longrightarrow +\infty} (-0.3)^{n} = 0$ . Ainsi, par somme, nous avons :

$\boxed{\lim\limits_{n \longrightarrow +\infty} u_{n} = 2}$

Corrigé de l’exercice 3 :

Les suites $(\displaystyle{\frac{1}{n})}_{n \in \N{*}}$ et $(\displaystyle{\frac{2}{n^{2}})}_{n \in \N^{*}}$ convergent toutes deux vers $0$ . Ainsi, par somme :

$\boxed{\lim\limits_{n \longrightarrow +\infty} u_{n} = 1}$

4. Convergence et limites

Exercice 1 :

On considère la suite géométrique $Un$ de raison $\displaystyle{\frac{1}{2}}$ telle que $u_4= 32$ . Alors pour tout $n \in \mathbb{N}$

a. $u_n = 32 + \displaystyle{\frac{n-4}{2}}$

b. $32 \times (\displaystyle{\frac{1}{2}})^n$

c. $32 \times (\displaystyle{\frac{1}{2})^{n-4}}$

b. $32 + (\displaystyle{\frac{1}{2})^{n-4}}$

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Corrigé de l’exercice 1 :

On sait que pour une suite géométrique de raison $q$ on peut écrire $u_n = u_0 \times q^n$

On a donc $u_4 = u_0 \times (\displaystyle{\frac{1}{2})}^4 = 32$
Donc $u_0 = \displaystyle{\frac{32}{(\displaystyle{\frac{1}{2})}^4}}$
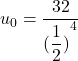
On peut en déduire $u_n = 32 \times (\displaystyle{\frac{1}{2})}^{n-4}$

Retrouvez d’autres exercices et corrigés des cours de maths niveau terminale D :

Exercices corrigés sur les récurrences en terminale D

Suites en Terminale D : exercices et corrigés

1. Suites récurrentes et étude de suites

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

2 – Vrai / Faux sur la monotonie

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

3 – Limites de suites

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

4. Convergence et limites

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales