Chapitres de maths en Terminale S2
Exercices et corrigés gratuits en terminale S2 sur les suites
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale S2
Beaucoup d’exercices sont classiques et permettent de progresser sur les suites numériques en terminale S2. Retrouvez ci-dessous quelques exercices corrigés qui vous seront utiles dans votre préparation du bac S2.
1. Récurrence et suites
Exercice 1 :
On considère la suite ![]() définie sur
définie sur ![]() par :
par :
![Rendered by QuickLaTeX.com \[ \left \{ \begin{array}{c @{=} c} u_{0} = 1 \\ u_{n+1} = \displaystyle{\frac{u_{n}}{\sqrt{u_{n}^{2}+1}}} \\ \end{array} \right. \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-78cd8459c010b2c6a25892502893ad03_l3.png)
Montrez que pour tout n,
![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé de l’exercice 1 :
![]()
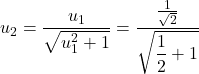
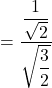
![]()
![]()
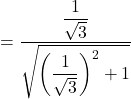
![]()
![]()
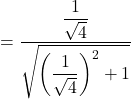
![]()
On peut donc conjecturer que ![]() .
.
Posons la propriété suivante : ![]() :
: ![]() .
.
Initialisation
![]() et
et ![]() donc
donc ![]() est vraie.
est vraie.
Hérédité
soit ![]() , supposons que
, supposons que ![]() est vraie. Montrons que
est vraie. Montrons que ![]() est vraie.
est vraie.
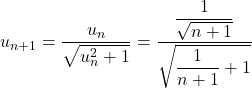
![]()
Ainsi ![]() est vraie.
est vraie.
Conclusion
![]() est vraie, c’est-à-dire :
est vraie, c’est-à-dire :
![]()
2 – Etude de deux suites
Question 1 :
Soient les suites: ![]() définie par
définie par ![]() et pour tout entier naturel
et pour tout entier naturel ![]() :
: ![]()
et ![]() par
par ![]()
Calculer ![]()
Question 2 :
![]() est:
est:
a. arithmétique et géométrique
b. arithmétique non géométrique
c. géométrique non arithmétique
d. aucune des trois propositions ci-dessus n’est correcte.
Question 3
(![]() ) est:
) est:
a. arithmétique et géométrique
b. arithmétique non géométrique
c. géométrique non arithmétique
d. aucune des trois propositions ci-dessus n’est correcte.
Question 4 :
Quel que soit ![]() :
: ![]()
a. ![]()
b. ![]()
![]()
d. aucune des trois propositions ci-dessus n’est correcte.
Question 5 :
La suite ![]() :
:
a. converge
b. diverge vers ![]()
c. diverge vers ![]()
d. aucune des trois propositions ci-dessus n’est correcte.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Corrigé de la question 1 :
On a ![]() donc
donc
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}U_1&=&-\displaystyle\frac{3}{2}\times 4+\displaystyle\frac{5}{2}\times 0+1\\ & &\\&=&-6+1=-5\end{array}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d595b079b512cc324d39e68b851b641f_l3.png)
Corrigé de la question 2 :
On a ![]()
=![]() n’est pas une constante
n’est pas une constante
Donc (Un) n’est pas arithmétique.
On a
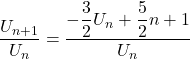
=![]() n’est pas une constante.
n’est pas une constante.
Donc ![]() n’est pas géométrique.
n’est pas géométrique.
Donc ![]() n’est pas arithmétique, ni géométrique!
n’est pas arithmétique, ni géométrique!
Corrigé de la question 3 :
On a
![]()
=![]()
=![]()
Donc ![]()
Donc ![]() est géométrique de raison
est géométrique de raison ![]()
Donc ![]() n’est pas une constante
n’est pas une constante
Donc ![]() n’est pas arithmétique
n’est pas arithmétique
Donc ![]() est géométrique non arithmétique
est géométrique non arithmétique
Corrigé de la question 4 :
![]() est géométrique de raison
est géométrique de raison ![]() donc pour tout entier naturel
donc pour tout entier naturel ![]() ,
, ![]() .
.
Or ![]()
Donc ![]() .
.
Or ![]() donc
donc ![]()
Donc pour tout entier naturel ![]() ,
, ![]()
Corrigé de la question 5 :
On sait que ![]() est géométrique de raison
est géométrique de raison ![]()
Donc ![]() n’est ni convergente, ni divergente vers
n’est ni convergente, ni divergente vers ![]() ou
ou ![]()
Or ![]() , donc
, donc ![]() n’est ni convergente, ni divergente vers
n’est ni convergente, ni divergente vers ![]() ou
ou ![]()
3 – Limites de suites numériques
Exercice 1 :
Calculer la limite quand ![]() de la suite suivante
de la suite suivante ![]()
Exercice 2 :
Calculer la limite quand ![]() de la suite suivante
de la suite suivante ![]() est
est
Exercice 3 :
Calculer la limite quand ![]() de la suite suivante
de la suite suivante ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé de l’exercice 1 :
![]() et
et ![]() . Donc, par somme :
. Donc, par somme :
![]()
Corrigé de l’exercice 2 :
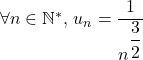 . Comme la puissance de
. Comme la puissance de ![]() au dénominateur est strictement positive, nous avons :
au dénominateur est strictement positive, nous avons :
![]()
Corrigé de l’exercice 3 :
La suite ![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() strictement supérieure à
strictement supérieure à ![]() . Ainsi, nous pouvons affirmer que
. Ainsi, nous pouvons affirmer que
![]()
4. Convergence et monotonie des suites
Exercice 1 :
On considère les deux suites ![]() et
et ![]() définies par
définies par
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l}{u_{0}=5} \\ {u_{n+1}=\displaystyle{\frac{3 u_{n}+v_{n}}{4}}} \end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-613daf5f7267ee7f6e7d166b4d6d0d36_l3.png)
et
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l}{v_{0}=15} \\ {v_{n+1}=\displaystyle{\frac{u_{n}+5 v_{n}}{6}}} \end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8b74ef297608a62f05aac8ab0f7a0270_l3.png)
On admet que ![]() converge vers
converge vers ![]() et que
et que ![]() converge vers
converge vers ![]() . Alors :
. Alors :
a. ![]()
b. ![]()
c. ![]()
d. On ne dispose pas assez d’informations pour comparer ![]() et
et ![]()
Exercice 2 :
On considère une suite ![]() strictement croissante de premier terme
strictement croissante de premier terme ![]() et la suite
et la suite ![]() définie pour tout
définie pour tout ![]() par
par ![]() . Alors la suite
. Alors la suite ![]() est :
est :
a. monotone et croissante.
b. monotone et décroissante.
c. non monotone
d. aucune des 3 réponses précédentes n’est exacte.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé de l’exercice 1 :
On passe à la limite dans l expression de ![]() .
.
On obtient ![]()
Donc ![]()
D’où ![]()
Corrigé de l’exercice 2 :
La suite ![]() est strictement croissante, de premier terme 2. Par conséquent, la suite
est strictement croissante, de premier terme 2. Par conséquent, la suite ![]() est strictement monotone de premier terme -5.
est strictement monotone de premier terme -5.
Par conséquent la suite ![]() est strictement monotone et décroissante.
est strictement monotone et décroissante.
Retrouvez d’autres exercices pour les terminales S2 et corrigés des cours de maths :
- Exercices et corrigés sur la fonction exponentielle en terminale S2
- Exercices et corrigés sur les intégrales en terminale S2
- Exercices et corrigés sur la fonction logarithme en terminale S2

