Chapitres Maths en Première

Cours sur le second degré en première

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Première

Ce cours en ligne en maths en première permettent aux élèves de réviser le chapitre du second degré qui leur sera également utile en terminale et durant les études supérieures. Les élèves de première peuvent aussi réviser d’autres chapitres d’algèbre tels que les suites numériques, les suites arithmétiques et géométriques, la dérivation ou encore le chapitre de probabilité et statistiques, il est possible de prendre un cours de maths particulier pour consolider vos notions sur le second dégrés en pre.

I. Equation du second degré : résumé

Dans ce paragraphe, on suppose que $a , b$ et $c$ sont réels et $a \neq 0$ .

On note $Q : x \mapsto a\,x^2 + b\, x + c$ .

1.1. Second degré : forme canonique de $P(x)$

On note $\Delta = b ^2 - 4\, a\,c$ .

$\displaystyle Q(x) = a \left ( \left (x + \frac {b} {2 \, a} \right ) ^2 - \frac{\Delta} {4 \, a^2} \right )$

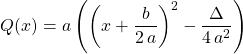
Pour retrouver la forme canonique, on écrit $Q(x) = a \left ( \displaystyle x ^2 + \frac b a \, x + \frac c a \right )$

et on écrit que $\displaystyle x ^2 + \frac b a \, x$ est le début du

développement de $\left (\displaystyle x + \frac b {2\, a} \right ) ^2$

$u(x) = \displaystyle x ^2 + \frac b a \, x + \frac c a$

$u(x) = \displaystyle \left ( x + \frac b {2\, a} \right ) ^2 - \left ( \frac b {2\, a}\right ) ^2 + \frac c a$

$u(x) = \displaystyle \left ( x + \frac b {2\, a} \right ) ^2 - \frac {b^2} {4\, a^2} + \frac c a$

$u(x) =\displaystyle \left ( x + \frac b {2\, a} \right ) ^2 + \frac {4\, a\, c - b ^2} {4\, a^2}$

$u(x) = \displaystyle \left ( x + \frac b {2\, a} \right ) ^2 - \frac {\Delta} {4\, a^2}$ .

1.2. Second degré : racines et factorisation

$\bullet$ Si $\Delta < 0$ , l’équation $Q(x) = 0$ n’a pas de racine dans $\mathbb{R}$ .

$\bullet$ Si $\Delta = 0$ , l’équation $Q(x) = 0$ a une racine double $\displaystyle x _ 0 = \frac {- b} {2\, a}$

et $Q(x) = a \, (x - x_0)^2$ .

$\bullet$ Si $\Delta > 0$ , l’équation $Q(x) = 0$ a deux racines réelles distinctes

$x_1 = \displaystyle \frac {- b - \sqrt{\Delta}} {2\, a}$ et $x_2 = \displaystyle \frac {- b + \sqrt{\Delta}} {2\, a}$

et $Q(x) = a\,(x - x_1) (x - x_2)$ .

👍 Une remarque utile : si $a \, c < 0$ , l’équation admet toujours deux racines réelles, qui sont de plus de signe contraire.

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

1.3. Second degré : signe de $Q(x)$

$\bullet$ Si $\Delta < 0$ , pour tout réel $x$ , $Q(x)$ est non nul et du signe de $a$ .

$\bullet$ Si $\Delta = 0$ , pour tout réel $x$ ,

$Q(x) \geqslant 0$ si $a > 0$ et $Q(x) \leqslant a$ si $a < 0$ .

On peut aussi écrire que $a \, Q(x) \geqslant 0$ et ne s’annule qu’en $x_0\,$ .

$\bullet$ Si $\Delta > 0$ ,

$\ast \; Q(x)$ est du signe de $-a$ entre les racines

$\ast \; Q(x)$ est du signe de $a$ à l’extérieur des racines.

👍 Conséquence pour placer un nombre $r$ entre les racines $x_1$ et $x_2\,$ , on calcule $a \, Q(r)$ .

$\ast$ Si $a\, Q(r) < 0$ , $r$ est entre les racines

$\ast$ Si $a \, Q(r) > 0$ , $r$ est à l’extérieur des racines.

La somme $S$ des racines est égale à $S = \displaystyle \frac {-b} {a}$ .

On détermine le signe de $\displaystyle \frac S 2 - r$

… Si $\displaystyle \frac S 2 - r > 0$ , $r$ est supérieur à la plus grande des racines de $Q$ .

… Si $\displaystyle \frac S 2 - r < 0$ , $r$ est inférieur à la plus petite des racines de $Q$ .

1.4. Second degré : somme et produit des racines.

$\bullet$ Si $\Delta > 0$ et si $x_1$ et $x_2$ sont les deux racines de $Q(x) = 0$ ,

$S = x_1 + x_2 = \displaystyle \frac {-b} {a}$

$P = x_1 \times x_2 = \displaystyle \frac {c} {a}$ .

$\bullet$ Utilisation 1 : Si l’on trouve une solution évidente $r$ de l’équation $Q(x) = 0$ , l’autre racine $r'$ peut être obtenue en utilisant

$\qquad r + r' = \displaystyle \frac {-b} {a}$ ou $r \, r' = \displaystyle \frac {c} {a}$ .

$\ast$ Si 1 est racine évidente de $Q(x) = 0$ l’autre racine est $\displaystyle \frac {c} {a}$ .

$\ast$ Si $-1$ est racine évidente de $Q(x) = 0$ , l’autre racine est $\displaystyle - \frac {c} {a}$ .

$\bullet$ Utilisation 2 : si l’on cherche deux réels $x$ et $y$ vérifiant $x + y = S$ et $x \, y = P$ , ce sont les racines (si elles existent) de $t ^2 - S \, t + P = 0$ .

(il est donc nécessaire et suffisant que $S^2 - 4\, P \geqslant 0$ pour que $x$ et $y$ existent.)

$\bullet$ Utilisation 3 : Si l’équation $Q(x) = 0$ admet deux racines distinctes $x_1$ et $x_2\,$ ,

$\ast$ si $\displaystyle \frac c a < 0$ , $x_1 \, x_2 < 0$ , les deux racines sont de signe contraire.

$\ast$ si $\displaystyle \frac c a > 0$ , $x_1 \, x_2 > 0$ , les deux racines sont de même signe.

… Elles sont strictement positives lorsque $S = \displaystyle -\frac b a > 0$

… Elles sont strictement négatives lorsque $S = \displaystyle -\frac b a < 0$

1.5. Second degré : interprétation graphique.

On note $\Gamma$ la parabole représentative de la fonction $Q$ .

$\ast$ Dans tous les cas, le point $\qquad S_0 \displaystyle \left ( \frac {- b} {2\, a}\,,\, Q \left ( \frac {- b} {2\, a}\right ) \right )$
est le sommet de la parabole.

$\ast$ La droite $\mathcal{D}$ d’équation $\displaystyle x = \frac {- b} {2\, a}$ est axe de symétrie de $\Gamma$ .

$\bullet$ Si $\Delta < 0$ , $\Gamma$ ne coupe pas la droite $Ox$

$\ast$ si $a > 0$ , la parabole est située au dessus de la droite $Ox$

$\ast$ si $a < 0$ , la parabole est située en dessous de la droite $Ox$ .

$\bullet$ Si $\Delta = 0$ , $\Gamma$ coupe la droite $Ox$ en un seul point : le sommet $S$ . La droite $Ox$ est tangente à $\Gamma$ en $S$ .

$\ast$ Si $a > 0$ , la parabole est située au dessus de la droite $Ox$

$\ast$ Si $a < 0$ , la parabole est située en dessous de la droite $Ox$ .

$\bullet$ Si $\Delta > 0$ , $\Gamma$ coupe la droite $Ox$ en deux points symétriques par rapport à la droite $\mathcal{D}$ .

$\ast$ si $a > 0$ , le sommet $S$ est situé sous la droite $Ox.$ La parabole est « tournée vers le haut « .

$\ast$ si $a < 0$ , le sommet $S$ est situé au dessus de la droite $Ox.$ La parabole est « tournée vers le bas ».

II. Des équations polynomiales de degré au moins égal à 3

2.1. Second degré : factorisation d’une fonction polynôme de degré 3

Factorisation d’une fonction polynôme de degré 3 dont on connaît une racine évidente $r$

On suppose que $\quad P(x) = a \, x ^3 + b \, x^2 + c \,x + d$ ( $a \neq 0$ ) et que $P(r) = 0$ .

Il existe trois réels $\alpha,\, \beta \,,\, \gamma$ tels que pour tout réel $x$ ,

$\quad P(x) = (x - r) (\alpha \, x ^2 + \beta \, x + \gamma )$ .

On calcule $\alpha,\, \beta \,,\, \gamma$ en développant le produit et en utilisant l’unicité de l’écriture d’une fonction polynôme (à ne pas confondre avec une fonction exponentielle), ce qui donne le système suivant :

$\qquad \qquad \displaystyle \left \{ \begin{matrix} \alpha = a \\ \beta - r \, \alpha = b \\ \gamma - r \, \beta = c \\ - \gamma \, r = d \end{matrix} \right.$

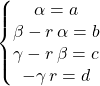
2.2. Deux factorisations

Si $n \in \mathbb{N}$ , $n \geqslant 2$ , si $x$ et $a$ sont réels,

$\bullet$ $x^n - 1 =$ $\quad (x - 1) (x^{n - 1} + x^{n - 2} + \cdots +x + 1)$

$\bullet$ $x^n - a^n$ est égal au produit de $(x - a)$ par $(x^{n - 1} + a\, x^{n - 2} + \cdots + a^{n - 2} x + a^{n - 1})$ .

La première relation est évidente pour $x = 1$ , car elle s’écrit $0 = 0$ .

Pour $x \neq 1$ , on rappelle que $\quad 1 + x + \cdots \, + x^{n - 1} = \displaystyle \frac {1 - x^ n} {1 - x}$

on multiplie cette relation par $1 - x$ .

Pour la deuxième relation, on effectue le produit :

$(x - a) (x^{n - 1} + \cdots + a^{n - 2} x + a^{n - 1})$

On obtient :

$x^{n} + a\, x^{n - 1} + \cdots +a^{n - 2} x^2 + a^{n - 1}\, x$

$-a\, x^{n - 1} - a^2 \, x^{n - 2} - \cdots- a^{n - 1} x - a^{n}$

et on simplifie …

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION