Chapitres de maths en Terminale D
Cours sur les nombres complexes et géométrie en Terminale D
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale D
Vous trouverez ci-dessous un cours de maths sur les nombres complexes proposé aux élèves de terminale D.
1. Ecriture algébrique et trigonométrique des complexes en terminale D
Le corps des nombres complexes ![]() peut être représenté par un plan. On parle du plan complexe. Tout nombre complexe d’affixe
peut être représenté par un plan. On parle du plan complexe. Tout nombre complexe d’affixe ![]() sera alors représenté par ses coordonnées dans une base orthonormée du plan. On distingue dès lors deux principaux systèmes de coordonnées :
sera alors représenté par ses coordonnées dans une base orthonormée du plan. On distingue dès lors deux principaux systèmes de coordonnées :
– les coordonnées cartésiennes;
– les coordonnées polaires.
Coordonnées cartésiennes et écriture algébrique
Soit ![]() un repère orthonormé du plan. Ce repère est dit cartésien si les vecteurs de la base
un repère orthonormé du plan. Ce repère est dit cartésien si les vecteurs de la base ![]() et
et ![]() sont fixes. Dans un tel repère, tout point
sont fixes. Dans un tel repère, tout point ![]() d’affixe
d’affixe ![]() est déterminé par le couple de réels
est déterminé par le couple de réels ![]() tels que :
tels que :
![]()
Les réels ![]() sont les coordonnées cartésiennes du point
sont les coordonnées cartésiennes du point ![]() dans la base
dans la base ![]() . Dans le vocabulaire des nombres complexes,
. Dans le vocabulaire des nombres complexes, ![]() est appelé partie réelle et
est appelé partie réelle et ![]() partie imaginaire. Ces coordonnées permettent d’écrire l’écriture algébrique du nombre complexe
partie imaginaire. Ces coordonnées permettent d’écrire l’écriture algébrique du nombre complexe ![]() :
:
![]()
Coordonnées polaires et écriture trigonométrique ou exponentielle
Pour introduire les coordonnées polaires, il convient tout d’abord de tracer le cercle trigonométrique et de placer un point M quelconque sur ce cercle. On définit alors un repère orthonormé ![]() tel qu’indiqué sur la figure ci-dessous :
tel qu’indiqué sur la figure ci-dessous :
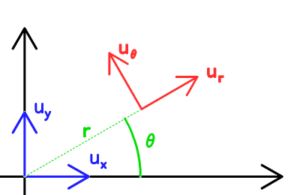
– le vecteur radial ![]() est un vecteur unitaire dirigé suivant le vecteur
est un vecteur unitaire dirigé suivant le vecteur ![]() ; il suit le déplacement du point M;
; il suit le déplacement du point M;
– le vecteur orthoradial ![]() est un vecteur unitaire orthogonal au vecteur
est un vecteur unitaire orthogonal au vecteur ![]() , avec un angle de
, avec un angle de ![]() dans le sens trigonométrique (anti-horaire).
dans le sens trigonométrique (anti-horaire).
Dans un tel repère, le point M d’affixe ![]() est décrit par le couple de réels
est décrit par le couple de réels ![]() , avec
, avec ![]() et
et ![]() , tels que :
, tels que :
![]()
Dans l’expression ci-dessus, la variable ![]() n’apparaît pas explicitement. Cependant, elle est bien présente dans le vecteur
n’apparaît pas explicitement. Cependant, elle est bien présente dans le vecteur ![]() , dont l’expression dans la base cartésienne
, dont l’expression dans la base cartésienne ![]() est donnée par:
est donnée par:
![]()
Grâce aux coordonnées polaires ![]() , nous pouvons écrire la forme trigonométrique du complexe
, nous pouvons écrire la forme trigonométrique du complexe ![]() :
:
![]()
Le nombre ![]() est le module de
est le module de ![]() , noté
, noté ![]() , et le réel
, et le réel ![]() est appelé l’argument de
est appelé l’argument de ![]() . Nous pouvons donc écrire:
. Nous pouvons donc écrire:
![]()
![]()
![]()
Nous pouvons dès lors introduire la notation exponentielle complexe, qui s’avérera très utile par la suite :
![]()
On obtient ainsi la forme exponentielle du nombre complexe ![]() :
:
![]()
La figure ci-dessous représente le cercle trigonométrique avec les angles remarquables.

Liens entre les coordonnées cartésiennes et polaires : module et argument
Il est très facile de passer des coordonnées cartésiennes aux coordonnées polaires, et vice-versa. En effet, si l’on observe la figure précédente, un théorème de Pythagore et les relations de trigonométrie nous donnent :
![]()
![]() , si
, si ![]()
![]() , si
, si ![]()
![]() , si
, si ![]()
On peut donc aisément passer des coordonnées ![]() aux coordonnées
aux coordonnées ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2 – Ensemble des nombres complexes en terminale D
L’ensemble des nombres complexes peut être noté :
![]() ,
, ![]()
L’ensemble des complexes ![]() contient donc l’ensemble des réels
contient donc l’ensemble des réels ![]() . Les lois d’addition et de multiplication sont étendues à
. Les lois d’addition et de multiplication sont étendues à ![]() de manière identique.
de manière identique.
ATTENTION : il n’y a pas de relation d’ordre sur ![]() , autrement dit il n’est pas possible d’affirmer qu’un nombre complexe
, autrement dit il n’est pas possible d’affirmer qu’un nombre complexe ![]() est inférieur ou supérieur à un nombre
est inférieur ou supérieur à un nombre ![]() . On pourra seulement écrire :
. On pourra seulement écrire :
![]() ou
ou ![]()
Le nombre ![]() indiqué plus haut est appelé nombre imaginaire pur. Il est défini par l’équation :
indiqué plus haut est appelé nombre imaginaire pur. Il est défini par l’équation : ![]()
Définition : Conjugué d’un complexe
Soit ![]() , dont l’écriture algébrique est
, dont l’écriture algébrique est ![]() , avec
, avec ![]() .
.
Le complexe conjugué de ![]() , noté
, noté ![]() , est défini par:
, est défini par:
![]()
Propriétés : soient ![]() et
et ![]() deux nombres complexes :
deux nombres complexes :
![]() est réel si et seulement si sa partie imaginaire est nulle, autrement dit ssi
est réel si et seulement si sa partie imaginaire est nulle, autrement dit ssi ![]() ;
;
![]() est imaginaire pur si et seulement si sa partie réelle est nulle, autrement dit ssi
est imaginaire pur si et seulement si sa partie réelle est nulle, autrement dit ssi ![]() ;
;
Les points d’affixes ![]() et
et ![]() sont symétriques par rapport à l’axe des réels (abscisses);
sont symétriques par rapport à l’axe des réels (abscisses);
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Si ![]() , alors
, alors ![]() ;
;
Si ![]() , alors
, alors ![]() ;
;
Si ![]() , alors
, alors ![]() .
.
Argument d’un nombre complexe non nul
Soient ![]() et
et ![]() deux nombres complexes non nuls. On notera
deux nombres complexes non nuls. On notera ![]() l’argument de
l’argument de ![]() . Nous avons alors :
. Nous avons alors :
![]() ssi
ssi ![]()
![]() ;
;
![]() est imaginaire pur ssi
est imaginaire pur ssi ![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Module d’un nombre complexe
Soit ![]() . On rappelle que son module est défini par :
. On rappelle que son module est défini par :
![]()
Soient ![]() et
et ![]() deux complexes :
deux complexes :
![]() ;
;
![]() si et seulement si
si et seulement si ![]() ;
;
![]() : IMPORTANT : on parle d’inégalité triangulaire;
: IMPORTANT : on parle d’inégalité triangulaire;
![]() ;
;
Si ![]() , alors
, alors ![]() ;
;
![]() ;
;
Si ![]() ,
, ![]() .
.
Formules d’Euler : liens entre fonctions trigonométriques et exponentielle complexe
Nous avons vu plus haut qu’un nombre complexe ![]() peut s’écrire sous les formes équivalentes:
peut s’écrire sous les formes équivalentes:
![]()
![]()
Ainsi, on remarque tout de suite que :
![]()
![]()
Par ailleurs, en exploitant les relations ![]() et
et ![]() , nous obtenons les formules d’Euler :
, nous obtenons les formules d’Euler :
![]()
![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3 – Equations du second degré dans 
La résolution des équations du second degré diffère quelque peu lorsque l’inconnue ![]() est complexe.
est complexe.
Cas n°1 : équation ![]() , avec
, avec ![]()
Il faut ici distinguer 2 cas de figure suivant le signe de la constante ![]() .
.
cas 1.1 : ![]()
Si ![]() , alors
, alors ![]() ;
;
Si ![]() , alors
, alors ![]() .
.
Une égalité entre 2 nombres complexes contient toujours 2 informations : le module et l’argument. Nous avons ainsi :
![]()
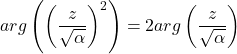
![]()
On en déduit tout d’abord que ![]() .
.
De plus, l’argument d’un nombre réel strictement positif vaut 0 modulo ![]() (attention, il vaut
(attention, il vaut ![]() pour un nombre réel négatif).
pour un nombre réel négatif).
Ainsi, l’équation sur les arguments nous donne:
![]()
![]() ,
, ![]()
![]() ,
, ![]()
Finalement, le nombre ![]() s’avère être un nombre réel, dont le module vaut
s’avère être un nombre réel, dont le module vaut ![]() , et l’argument
, et l’argument ![]() ou
ou ![]() (module
(module ![]() ).
).
Autrement dit :
![]()
cas 1.2 : ![]()
Dans le cas réel, l’équation ![]() n’admet aucune solution. Mais dans
n’admet aucune solution. Mais dans ![]() , les choses sont différentes !
, les choses sont différentes !
A nouveau, le module et l’argument nous fournissement deux équations :
![]()
![]()
=![]()
Ainsi, ![]() est un nombre imaginaire pur, de module
est un nombre imaginaire pur, de module ![]() , et d’argument
, et d’argument ![]()
![]() .
.
Finalement :
![]()
Cas n°2 : équation ![]() , avec
, avec ![]()
A l’instar du cas réel, on commence par calculer le discriminant du polynôme :
![]()
Comme les coefficients ![]() ,
, ![]() et
et ![]() sont réels, nous pouvons étudier le signe de
sont réels, nous pouvons étudier le signe de ![]() :
:
Si ![]() : le polynôme du 2nd degré admet deux racines réelles distinctes :
: le polynôme du 2nd degré admet deux racines réelles distinctes :
![]()
![]()
Si ![]() : le polynôme admet une racine réelle double :
: le polynôme admet une racine réelle double : ![]() ;
;
Si ![]() : le polynôme admet 2 racines complexes conjuguées :
: le polynôme admet 2 racines complexes conjuguées :
![]()
![]()
Retrouvez d’autres chapitres à travailler en cours de maths en terminale D :

