Chapitres de maths en 1ère
Dérivation en 1ère
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Première
Ce cours en ligne de maths en première présente est utile pour les élèves souhaitant s’entraîner à la dérivation en première : nombre dérivé, fonction dérivée, formule dérivée, etc.. D’autres chapitres et des profs de maths en ligne de première sont également disponibles sur notre site comme, le second degré, les suites numériques ou encore les séries arithmétiques et géométriques.
Nombre dérivé : définition et exemples fondamentaux
Définition d’un nombre dérivé
Soit ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() , et soit
, et soit ![]() On définit le nombre dérivé de
On définit le nombre dérivé de ![]() en
en ![]() le nombre noté
le nombre noté ![]() tel que :
tel que :
![]()
Nombre dérivé : exemples fondamentaux
Exemple 1 : la fonction carré
Posons ![]() , et calculons le taux d’accroissement de
, et calculons le taux d’accroissement de ![]() entre
entre ![]() et
et ![]() , où a est un nombre quelconque et
, où a est un nombre quelconque et ![]() :
:
![]()
![]()
![]()
![]()
![]()
Ainsi, ![]()
![]()
![]()
![]()
Quelle que soit la valeur de ![]() , le nombre dérivé de
, le nombre dérivé de ![]() en a est
en a est ![]()
Exemple 2 : la fonction cube
Posons ![]() , et calculons le taux d’accroissement de
, et calculons le taux d’accroissement de ![]() entre
entre ![]() et
et ![]() , où
, où ![]() est un nombre quelconque et
est un nombre quelconque et ![]() :
:
![]()
![]()
![]()
![]()
![]()
Ainsi, ![]()
![]()
![]()
Quelle que soit la valeur de ![]() , le nombre dérivé de
, le nombre dérivé de ![]() en
en ![]() est
est ![]()
Exemple 3 : la fonction racine carrée
Posons ![]()
![]()
![]()
![]() x
x ![]()
![]()
![]()
![]()
Ainsi ![]()
![]()
![]()
Quelle que soit la valeur de ![]() , le nombre dérivé de
, le nombre dérivé de ![]() en
en ![]() est :
est :
![]()
Exemple 4 : la fonction inverse
Posons ![]()
![]()
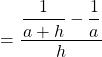
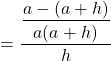
![]()
![]()
Ainsi ![]()
![]()
![]()
Quelle que soit la valeur de ![]() , le nombre dérivé de
, le nombre dérivé de ![]() en
en ![]() est
est ![]()
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Equation de la tangente
Définition d’une tangente
Soit ![]() la courbe représentative d’une fonction
la courbe représentative d’une fonction ![]() définie sur un intervalle
définie sur un intervalle ![]() . Soit
. Soit ![]() . On appelle tangente à
. On appelle tangente à ![]() au point d’abscisse a la droite de coefficient directeur
au point d’abscisse a la droite de coefficient directeur ![]() passant par le point de coordonnées
passant par le point de coordonnées ![]()
Equation d’une tangente
Soit ![]() la courbe représentative d’une fonction
la courbe représentative d’une fonction ![]() définie sur un intervalle
définie sur un intervalle ![]() . Soit
. Soit ![]() . L’équation réduite de la tangente à
. L’équation réduite de la tangente à ![]() au point d’abscisse a est :
au point d’abscisse a est : ![]()
Fonction dérivée
Définition d’une fonction dérivée
Soit ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() . On définit la fonction dérivée de
. On définit la fonction dérivée de ![]() comme étant la fonction :
comme étant la fonction : ![]() où
où ![]() est le nombre dérivé de
est le nombre dérivé de ![]() en
en ![]() . Si
. Si ![]() est définie sur un intervalle
est définie sur un intervalle ![]() inclus dans I alors on dit que
inclus dans I alors on dit que ![]() est dérivable sur
est dérivable sur ![]() . Attention à ne pas confondre fonction dérivée et fonction exponentielle !
. Attention à ne pas confondre fonction dérivée et fonction exponentielle !
Dérivées de référence
D’après les exemples 1, 2, 3 et 4, on peut écrire :
1. Si ![]() alors
alors ![]() sur
sur ![]() .
.
2. Si ![]() alors
alors ![]() sur
sur ![]() .
.
3. Si ![]() alors
alors ![]() sur
sur ![]() (la fonction n’est pas dérivable en 0).
(la fonction n’est pas dérivable en 0).
4. Si ![]() alors
alors ![]() sur
sur ![]() et sur
et sur ![]() .
.
5. Si ![]() , alors
, alors ![]()
Dérivée d’une fonction composée
Soit la fonction ![]() , où
, où ![]() et
et ![]() sont deux nombres réels. Alors, sa fonction dérivée est :
sont deux nombres réels. Alors, sa fonction dérivée est : ![]()
Exemple
![]() , définie sur
, définie sur ![]() .
.
Ici, ![]() et
et ![]() .
.
![]() donc
donc ![]() soit :
soit :
![]() , définie sur
, définie sur ![]()
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
Exemple (produit d’un nombre et d’une fonction)
![]()
On pose alors :
![]() et
et ![]() Comme
Comme ![]() , on a :
, on a :
![]()
Exemple (différence)
![]()
La dérivée ![]() est
est
a. ![]()
b. ![]()
c. ![]()
Variation d’une fonction dérivée
Soit ![]() une fonction dérivable sur un intervalle
une fonction dérivable sur un intervalle ![]() .
.
![]() est strictement croissante sur
est strictement croissante sur ![]() pour tout
pour tout ![]() de
de ![]()
![]() est strictement décroissante sur
est strictement décroissante sur ![]() pour tout
pour tout ![]() de
de ![]() .
.
Conséquence : pour étudier les variations d’une fonction, il suffit d’étudier le signe de sa dérivée.
Exemple
Soit ![]()
Sa dérivée est : ![]() . C’est un polynôme de second degré, dont le discriminant est :
. C’est un polynôme de second degré, dont le discriminant est :
![]()
![]()
Ainsi, ![]() est du signe du coefficient de
est du signe du coefficient de ![]() , c’est-à-dire ici positif.
, c’est-à-dire ici positif.
![]() donc
donc ![]() est strictement croissante sur
est strictement croissante sur ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
Extremum local d’une fonction dérivée
Soit ![]() une fonction dérivable sur un intervalle
une fonction dérivable sur un intervalle ![]() . Soit
. Soit ![]()
On dit que ![]() admet un extremum local en
admet un extremum local en ![]() si
si ![]() et si, pour
et si, pour ![]() ,
, ![]() et
et ![]() n’ont pas le même signe.
n’ont pas le même signe.
Cet extremum local peut être :
![]() un minimum si :
un minimum si : 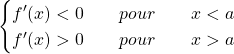
![]() un maximum si :
un maximum si : 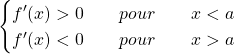
Le cours complet sur la dérivation en 1ère est disponible sur notre application mobile PrepApp.

