Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Avis Google France
★★★★★ 4,8 sur 5

Arithmétique seconde exercices corrigés

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Seconde

1. Exercices d’arithmétique : application

Exercice d’arithmétique 1 : On rappelle quelques critères de divisibilité :

$\bullet$ Divisibilité par 3. Un entier naturel est divisible par 3 si et seulement si la somme des nombres dans sa représentation décimale est divisible par 3.

Par exemple, 9018 est divisible par 3 car 9+0+1+8=18 est divisible par 3 alors que 1597 n’est pas divisible par 3 car 1+5+9+7=22 n’est pas divisible par 3.

$\bullet$ Divisibilité par 9. Un entier naturel est divisible par 9 si et seulement si la somme des nombres dans sa représentation décimale est divisible par 9.

Par exemple, 279018 est divisible par 9 car 2+7+9+0+1+8=27 est divisible par 9 alors que 1586 n’est pas divisible par 9 car 1+5+8+7=21 n’est pas divisible par 9.

$\bullet$ Divisibilité par 11. Un entier naturel est divisible par 11 si et seulement si la différence entre les nombres de rangs impairs et les nombres de rangs pairs dans sa représentation décimale est divisible par 11.

Par exemple, 957396 est divisible par 11 car $\big(9+7+9\big)-\big(5+3+6\big)=11$ est divisible par 11 alors que 19872 n’est pas divisible par 11 car

$\big(1+8+2\big)-\big(9+7\big)=-5$ n’est pas divisible par 11.

Déterminer une écriture sous la forme $\dfrac{p}{q}$ avec $p\in \mathbb{Z}$ et $q\in \mathbb{N}^*$ .

- Question 1 :

$\bullet$ $0,125$

$\bullet$ $-\sqrt{\dfrac{169}{256}}$

$\bullet$ $\sqrt{\dfrac{1}{4}}\times \sqrt{9}$

- Question 2 :

$\bullet$ $\dfrac{2\times 10^{-4}}{5\times 10^{-3}}$

$\bullet$ $\dfrac{121}{143}$

$\bullet$ $5$

Exercice d’arithmétique 2 : Soit $n$ un entier naturel et $n=3q+r$ avec $r\in \{0,1,2\}$ la division euclidienne de $n$ par $3$ .

- Question 1 :

Montrer que si $n$ n’est pas divisible par $3$ , alors $n^2$ n’est pas divisible par $3$ .

- Question 2 :

Que peut-on dire de l’implication suivante : $n^2$ divisible par $3$ entraîne $n$ divisible par $3$

- Question 3 :

Montrer que s’il existe deux entiers $p$ et $q$ premiers entre eux tels que $\sqrt{3}=\dfrac{p}{q}$ alors $p$ est divisible par $3$ .

- Question 4 :

Démontrer que $\sqrt{3}$ n’est pas rationnel.

Exercice d’arithmétique 3 : On admet que pour un nombre premier (positif) $p$ , $\sqrt{p}$ est irrationnel.

Simplifier les nombres suivants puis donner le plus petit ensemble de nombres auquel il appartient. On demande de montrer les étapes de calculs

$\bullet$ $\dfrac{25}{4}+\dfrac{17}{8}-\dfrac{13}{16}$

$\bullet$ $-5\times 10^{-2}+13\times 10^{-3}$

$\bullet$ $\big(\sqrt{2}-\sqrt{5}\big)\big(\sqrt{2}+\sqrt{5}\big)$

$\bullet$ $\big(\sqrt{4}-\sqrt{36}\big)^2$

$\bullet$ $\dfrac{5}{10}\times\big(5-\dfrac{7}{5}\big)-\dfrac{5}{3}\times \dfrac{21}{10}$

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

2. Exercice d’arithmétique en seconde : Aller plus loin

Exercice d’arithmétique 1 : Le tableau suivant donne une série de calculs à partir des deux nombres : $n=48$ et $p=18$

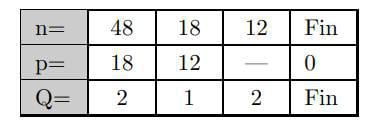
a) Ce tableau correspond à un algorithme vu en classe de troisième, lequel ?

b) Compléter ce tableau.

c) Le programme suivant traduit l’algorithme dans le tableau précédent

Déterminer le nombre de passages dans la boucle while.

Exercice d’arithmétique 2 : Pour n=64 et p=27, à partir du programme dans la question précédente, compléter le tableau suivant :

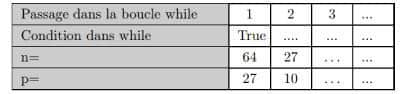
On peut rajouter autant de colonnes que nécessaires.

3. Exercice arithmétique : Modélisation

Exercice arithmétique 1 : L’algorithme de Kaprekar consiste à associer à tout nombre entier naturel $n$ le nombre $K(n)$ généré de la façon suivante:

$\bullet$ On considère les chiffres de l’écriture décimal du nombre $n$ . On forme le nombre $n_1$ en rangeant ces chiffres dans l’ordre croissant et le nombre $n_2$ en les rangeant dans l’ordre décroissant.

$\bullet$ On pose $K(n)=n_2-n_1$ . On itère ensuite le processus en repartant du nombre $K(n)$ .

Par exemple, si on choisit $n = 634$ , on obtient : $n_1 = 346$ et $n_2 = 643$ d’où $K(634) = 643 - 346 = 297$ . En itérant le processus, on obtient successivement : $K(297) = 693 ; K(693) = 594 ; K(594) = 495 ; K(495) = 495$ . Ensuite, tous les résultats sont égaux à $495$ .

1. Montrer que l’algorithme appliqué au nombre 5 294 conduit aussi à un nombre entier $p$ tel que $K(p) = p$ .

Exercice arithmétique 2: On effectue à la calculatrice les calculs ci-dessous :

$123^2 - 122^2 - 121^2 + 120^2 = 4$

$45^2 - 44^2 - 43^2 + 42^2 = 4$

1. Tester ce résultat surprenant sur une autre série de quatre nombres consécutifs et émettre une conjecture.

2. Prouver que la conjecture faite précédemment est vraie.

3. Pour un entier naturel $n$ , compléter les programmes en Python suivants pour qu’ils retournent à l’entier 4. Donner l’algorithme qui a le moins d’opérations.

Corrigé exercices arithmétique : partie application

Corrigé exercice arithmétique 1, question 1 :

On a :

$0,125 = 125\times 10^{-3}$

$0,125 = \dfrac{125}{10^{3}}$

$0,125= \dfrac{125}{1000}$

D’où, sous la forme $\dfrac{p}{q}$ , $0,125= \dfrac{125}{1000}$ avec $p=125 \in \mathbb{Z}$ et $q=1000 \in \mathbb{N}^*$ .

On rappelle que pour deux nombres positifs $a$ et $b$ , $\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}$
Alors :

$-\sqrt{\dfrac{169}{256}}= -\dfrac{\sqrt{169}}{\sqrt{256}}$

$-\sqrt{\dfrac{169}{256}}= -\dfrac{\sqrt{13^2}}{\sqrt{16^2}}$

$-\sqrt{\dfrac{169}{256}}= -\dfrac{13}{16}$

D’où, sous la forme $\dfrac{p}{q}$ , $-\sqrt{\dfrac{169}{256}}= \dfrac{-13}{16}$ avec $p=-13 \in \mathbb{Z}$ et $q=16 \in \mathbb{N}^*$ .

$\sqrt{\dfrac{1}{4}}\times \sqrt{9} = \dfrac{\sqrt{1}}{\sqrt{4}}\times \sqrt{3^2}$

$\sqrt{\dfrac{1}{4}}\times \sqrt{9} = \dfrac{\sqrt{1^2}}{\sqrt{2^2}}\times 3$

$\sqrt{\dfrac{1}{4}}\times \sqrt{9} = \dfrac{1}{2}\times 3$

D’où, sous la forme $\dfrac{p}{q}$ , $\sqrt{\dfrac{1}{4}}\times \sqrt{9}=\dfrac{3}{2}$ avec $p=3 \in \mathbb{Z}$ et $q=2 \in \mathbb{N}^*$ .

Corrigé exercice arithmétique 1, question 2 :

On rappelle que $\dfrac{a^{n}}{a^{m}}=\dfrac{1}{a^{m-n}}$ . Alors:

$\dfrac{2 \times 10^{-4}}{5\times 10^{-3}}= \dfrac{2}{5\times 10^{-3-(-4)}}$

$\dfrac{2 \times 10^{-4}}{5\times 10^{-3}}= \dfrac{2}{5\times 10^{-3+4}}$

$\dfrac{2 \times 10^{-4}}{5\times 10^{-3}}= \dfrac{2}{5\times 10^{1}}$

D’où, sous la forme $\dfrac{p}{q}$ , $\dfrac{2 \times 10^{-4}}{5\times 10^{-3}}= \dfrac{2}{50}$ avec $p=2 \in \mathbb{Z}$ et $q=50 \in \mathbb{N}^*$ .

$\dfrac{121}{143}$ est déjà sous forme de fraction $\dfrac{p}{q}$ avec $p=121 \in \mathbb{Z}$ et $q=143 \in \mathbb{N}^*$ .

Sous la forme $\dfrac{p}{q}$ , $5=\dfrac{5}{1}$ avec $p=5 \in \mathbb{Z}$ et $q=1 \in \mathbb{N}^*$ .

Corrigé exercice arithmétique 2, question 1 :

On a pour $n\in \mathbb{N},\ n=3q+r$ avec $r\in \{0,1,2\}$ et $q \in \mathbb{N}$ .

On suppose que $n$ n’est pas divisible par $3$ .

Donc, $r\in \{1,2\}$ et:

$n^2= (3q+r)^2$

$n^2= (3q+r)(3q+r)$

$n^2= 9q^2+3qr+3qr+r^2$

$n^2= 9q^2+6qr+r^2$

$n^2= 3(3q^2+2qr)+r^2$

On veut montrer par la suite que $n^2$ est sous la forme $n^2= 3p+1$ pour tout $r\in \{1,2\}$ .

Par disjonction de cas :

$\bullet$ Si $r=1$ , alors $r^2=1$ . Donc, $n^2= 3p+1$ avec $p= 3q^2+2q$ ;

$\bullet$ Si $r=2$ , alors $r^2=4=3\times 1+1$ . Donc,

$n^2= 3p+1$ avec $p= (3q^2+4q)+1$ .

Dans tous les cas, il existe un entier $p$ tel que $n^2=3p+1$ .

Donc, si $n$ n’est pas divisible par $3$ , alors $n^2$ n’est pas divisible par $3$ .

Corrigé exercice arithmétique 2, question 2 :

Par contraposition par rapport à la première question, l’affirmation suivante est vraie :

$n^2$ divisible par $3$ entraîne $n$ divisible par $3$

Corrigé exercice arithmétique 2, question 3 :

On suppose qu’il existe deux entier $p$ et $q$ premiers entre eux tels que \par\noindent $\sqrt{3}=\dfrac{p}{q}$ . On a:

$\sqrt{3} = \dfrac{p}{q} \Longleftrightarrow \sqrt{3}q=p$

$\sqrt{3} = \dfrac{p}{q} \Longleftrightarrow 3q^2$

= $p^2$ (On passe au carré)

Donc, $p^2$ est divisible par $3$ . D’après la question précédente, $p$ est divisible par $3$ .

Corrigé exercice arithmétique 2, question 4 :

Par l’absurde.

On suppose que $\sqrt{3}$ est rationnel. Alors, il existe $p\in \mathbb{Z},\ q\in \mathbb{N}^*$ et $p$ et $q$ sont deux nombres premiers entre eux tels que $\sqrt{3}=\dfrac{p}{q}$ .

D’après la question 3. : $\sqrt{3}=\dfrac{p}{q}$ entraîne $3q^2=p^2$ et $p$ est divisible par $3$ . C’est-à-dire $p=3k$ pour un entier $k\in \mathbb{N}$ .

$3q^2 = p^2\hbox{ et }p = 3k \Longleftrightarrow 3q^2 = (3k)^2$

$3q^2 = p^2\hbox{ et }p = 3k \Longleftrightarrow 3q^2 = 3^2k^2$

$3q^2 = p^2\hbox{ et }p = 3k \Longleftrightarrow q^2 = \dfrac{9}{3}k^2$

$3q^2 = p^2\hbox{ et }p = 3k \Longleftrightarrow q^2 = 3k^2$

Ce qui montre que $q^2$ est divisible par $3$ . Donc, $q$ est divisible par 3.

Par conséquent, $3$ divise $p$ et $q$ . Ce qui contredit l’hypothèse selon laquelle $p$ et $q$ sont premiers entre eux.

Corrigé exercice arithmétique 3 :

On a :

$\dfrac{25}{4}+\dfrac{17}{8}-\dfrac{13}{16} = \dfrac{25\times 4 }{4\times 4}+\dfrac{17\times 2}{8\times 2}-\dfrac{13}{16}$

$\dfrac{25}{4}+\dfrac{17}{8}-\dfrac{13}{16} = \dfrac{100+34-13}{16}$

$\dfrac{25}{4}+\dfrac{17}{8}-\dfrac{13}{16}= \dfrac{121}{16}$

$\dfrac{25}{4}+\dfrac{17}{8}-\dfrac{13}{16}= 7,5625$

$\dfrac{25}{4}+\dfrac{17}{8}-\dfrac{13}{16}= 75625\times 10^{-4}$

Par conséquent, $\dfrac{25}{4}+\dfrac{17}{8}-\dfrac{13}{16}= \dfrac{75625}{10^{4}} \in \mathbb{D}$ .

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Corrigés des exercices d’arithmétique : partie aller plus loin

Corrigé exercice arithmétique 1 :

a) Ce tableau correspond à l’algorithme d’Euclide.

b) L’algorithme d’Euclide permet de calculer le Plus Grand Commun

Diviseur de deux nombres entiers $n$ et $p$ . C’est une division euclidienne successive qui part de la division de $n$ par $p$ suivie par les divisions du dernier diviseur par le dernier reste. La division s’arrête quand le reste vaut $0$ ou $1$ .

$48 = 2\times 18 +12$

$18 = 1\times 12 + 6$

$12 = 2\times 6 +0$

Ce qui permet d’obtenir le résultat suivant:

n = 48 | 18 | 12 | Fin

p = 18 | 12 | 6 | 0

Q = 2 | 1 | 2 | Fin

c) Le nombre de passage dans la boucle while:

$\bullet$ Quand n=48 et p=18, le reste $n%p$ =12 au 1er passage.

$\bullet$ Quand n=18 et p=12, le reste n%p=6 au 2ème passage.

$\bullet$ Quand n=12 et p=6, le reste $n%p$ =0 au 3ème et dernier passage.

Car, la boucle while ne pourra plus continuer quand n%p = 0 ou n%p = 1.
Donc, l’algorithme passe 3 fois dans la boucle while.

Corrigé exercice arithmétique 2 :

Pour $n=64$ et $p=27$ , on le tableau complété à partir l’algorithme suivant : Passage dans la boucle while : 1 | 2 | 3 | 4

Condition dans while : True | True | True | False

n = 64 | 27 | 10 | 7

p = 27 | 10 | 7 | 3

L’algorithme se termine car le reste de la division euclidienne de 7 par 3 est de 1. C’est-à-dire que $64$ et $27$ sont premiers entre eux.

Corrigé exercice arithmétique : partie modélisation

Corrigé exercice arithmétique 1 :

Soit $K(n)$ le nombre généré par algorithme de Kaprekarde associé au nombre entier naturel $n$

Pour $n=5 294$ , on a: K(5 294)=9 542-2 459=7 083;

K(7083)=8730-378=8352; K(8352)=8532-2358=6174; K(6174)=7641-1467=6174.

D’où, appliqué à 5 294, l’algorithme conduit aussi à un nombre entier p=6174 tel que $K(p) = p$ .

Corrigé exercice arithmétique 2 :

1 – Si on prend la série des nombres 17, 18, 19 et 20, on a:

$20^2-19^2-18^2+17^2= 400-361-324+289$

$20^2-19^2-18^2+17^2= 39-35$

$20^2-19^2-18^2+17^2= 4$

On peut conjecturer que pour quatre nombres entiers consécutifs $i$ , $(i+1)$ , $(i+2)$ et $(i+3)$ , on a $(i+3)^2-(i+2)^2-(i+1)^2+i^2=4$

2 – Par la formule de l’identité remarquable $(a+b)^2= a^2+2ab+b^2$ , l’expression $(i+3)^2-(i+2)^2-(i+1)^2+i^2$ est égale à :

$(i^2+6i+9)-(i^2+4i+4)-(i^2+2i+1)+i^2$

Ce qui donne: $i^2-i^2+i^2-i^2+(9-6-4+1)i+9-4-1=4$

Donc, pour tout entier naturel $i$ , $(i+3)^2-(i+2)^2-(i+1)^2+i^2=4$

3 – Le premier programme a moins d’opérations que le deuxième.

a) ALGO 1

def somme1 ( $n$ : int) :

Somme = n**2 – (n+1) ** 2 +

(n+2) ** 2 – (n+3) ** 3

return Somme

b) ALGO 2

def somme1 ( $n$ : int) :

Somme = 0

for i in range(0 , 4) : Signe = -1

if i == 0 or i ==3

Signe =+ 1

Somme = somme + Signe $* (n+ i) ** 2$

return Somme

Retrouvez d’autres cours en ligne de maths seconde sur notre site :

Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Arithmétique seconde exercices corrigés

1. Exercices d’arithmétique : application

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

2. Exercice d’arithmétique en seconde : Aller plus loin

3. Exercice arithmétique : Modélisation

Corrigé exercices arithmétique : partie application

Corrigé exercice arithmétique 1, question 1 :

Corrigé exercice arithmétique 1, question 2 :

Corrigé exercice arithmétique 2, question 1 :

Corrigé exercice arithmétique 2, question 2 :

Corrigé exercice arithmétique 2, question 3 :

Corrigé exercice arithmétique 2, question 4 :

Corrigé exercice arithmétique 3 :

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Corrigés des exercices d’arithmétique : partie aller plus loin

Corrigé exercice arithmétique 1 :

Corrigé exercice arithmétique 2 :

Corrigé exercice arithmétique : partie modélisation

Corrigé exercice arithmétique 1 :

Corrigé exercice arithmétique 2 :

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales