Chapitres de maths en Terminale S2
Exercices et corrigés sur les équations différentielles en Terminale S2
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale S2
Beaucoup d’exercices sont classiques et permettent de progresser sur les équations différentielles en terminale S2. Retrouvez ci-dessous quelques exercices corrigés qui vous seront utiles dans votre préparation du bac S2.
Questions équations différentielles en terminale S2
Question 1 :
Résoudre l’équation ![]()
En cherchant une solution particulière sous la forme ![]() où
où ![]() .
.
Question 2 :
Résoudre ![]()
En cherchant une solution particulière sous la forme ![]() .
.
Question 3 :
Résoudre l’équation
![]()
En cherchant une solution particulière sous forme d’une fonction polynôme de degré 3.
Exercices terminale S2: où il faut passer par une équation différentielle.
On se propose de déterminer toutes les fonctions ![]() définies et dérivables sur l’intervalle
définies et dérivables sur l’intervalle
![]() vérifiant l’équation différentielle
vérifiant l’équation différentielle
![]() .
.
Question 1
Si ![]() est solution de
est solution de ![]() , alors la fonction g définie sur l’intervalle
, alors la fonction g définie sur l’intervalle ![]() par
par ![]() est solution de l’équation différentielle
est solution de l’équation différentielle ![]() .
.
Question 2
Résoudre ![]() et en déduire toutes les solutions de
et en déduire toutes les solutions de ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé des questions sur les équations différentielles terminale S2
Question 1 :
La solution générale de l’équation ![]() est
est ![]() où
où ![]() .
.
Soit ![]()
Pour tout réel ![]() ,
, ![]()
Pour tout réel ![]() ,
, ![]()
ssi ![]() ssi
ssi ![]() .
.
L’ensemble des solutions est l’ensemble des fonctions
![]() où
où ![]() .
.
Question 2 :
La solution générale de l’équation ![]() est
est ![]() où
où ![]() .
.
Soit pour ![]() ,
, ![]()
![]()
![]()
![]()
Pour tout réel ![]() ,
,
![]()
ssi pour tout réel ![]() ,
,
![]()
![]()
ssi ![]()
ssi ![]()
ssi ![]() ,
, ![]()
Donc ![]() est une solution pariculière de l’équation.
est une solution pariculière de l’équation.
La solution générale de l’équation ![]() est
est ![]() où
où ![]() .
.
Question 3 :
![]() La solution générale de l’équation homogène
La solution générale de l’équation homogène ![]() soit
soit ![]() est
est ![]() où
où ![]() .
.
![]() Soit si
Soit si ![]() ,
, ![]()
![]()
Pour tout réel ![]() ,
,
![]()
ssi pour tout réel ![]()
![]()
![]()
ssi 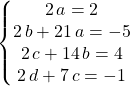
ssi 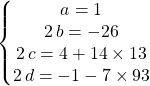
L’ensemble des solutions est l’ensemble des fonctions
![]() où
où ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé des exercices sur foncions sur les équations différentielles
Corrigé question 1
![]() est dérivable comme quotient de deux fonctions dérivables sur
est dérivable comme quotient de deux fonctions dérivables sur ![]() .
.
Si ![]() ,
, ![]()
donc ![]()
![]()
soit ![]() .
.
Corrigé question 2 en terminale S2
La solution générale de ![]() est la fonction
est la fonction ![]()
Grâce aux deux premières questions, ![]() est solution de
est solution de ![]() ssi
ssi ![]() est solution de
est solution de ![]() .
.
L’ensemble des solutions est l’ensemble des fonctions définies sur
![]() ,
, ![]() où
où ![]() .
.
Retrouvez d’autres exercices et corrigés des cours de maths niveau terminale S2 :
- Exercices corrigés sur la géométrie dans l’espace terminale S2
- Exercices complet corrigés sur les limites et derivibalité de fonctions en terminale S2
- Exercices en ligne terminale S2 : fonction exponentielle

