Chapitres de maths en Terminale D
Exercices et corrigés sur la géométrie dans l’espace en Terminale D
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale D
Vous trouverez ci-dessous des exercices corrigés gratuits sur la géométrie dans l’espace pour les élèves préparant le bac D.
QCM sur la géométrie dans l’espace en terminale D
Dans le repère ![]() de l’espace, on considère les points
de l’espace, on considère les points ![]() ,
, ![]() ,
, ![]() ; la droite
; la droite ![]() d’équation paramétrique:
d’équation paramétrique: 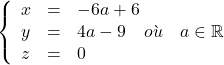
et le plan ![]() d’équation:
d’équation: ![]()
Question 1 :
Le point ![]() :
:
a. appartient à ![]() et à
et à ![]()
b. appartient à ![]() mais pas à
mais pas à ![]()
c. appartient à ![]() et à
et à ![]()
Question 2 :
Le triangle ![]() est:
est:
a. rectangle en ![]()
b. rectangle en ![]()
c. rectangle en ![]()
d. aucune des trois proposition ci-dessus n’est correcte.
Question 3 :
![]() et
et ![]() sont:
sont:
a. parallèles
b. sécantes non perpendiculaires.
c. perpendiculaires
d. aucune des trois proposition ci-dessus n’est correcte.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Corrigé du QCM de terminale D géométrie dans l’espace
Question 1 :
Supposons que ![]()
Alors il existe un réel ![]() tel que
tel que
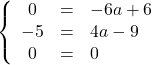
![]()
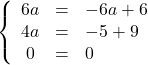
![]()
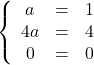
Ce réel ![]() existe, donc on a bien
existe, donc on a bien ![]()
De plus, on a ![]()
Donc les coordonnées du point ![]() vérifient l’équation du plan
vérifient l’équation du plan ![]()
Donc ![]()
Donc le point ![]() appartient à
appartient à ![]() et à
et à ![]()
Question 2 :
On a
![]()
=![]()
![]()
=![]()
![]()
=![]()
Donc ![]() ,
, ![]() et
et ![]()
Donc ![]() ,
, ![]() et
et ![]()
Donc ![]() n’est pas un triangle rectangle, ni en
n’est pas un triangle rectangle, ni en ![]() , ni en
, ni en ![]() , ni en
, ni en ![]()
Question 3 :
D’après sa représentation paramétrique, le vecteur 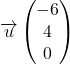 est un vecteur normal au plan
est un vecteur normal au plan ![]()
D’après son équation cartésienne, le vecteur, le vecteur 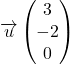 est un vecteur normal au plan
est un vecteur normal au plan ![]()
Supposons que ![]() et
et ![]() soient colinéaires, alors il existe un réel
soient colinéaires, alors il existe un réel ![]() tel que
tel que
![]()
Donc 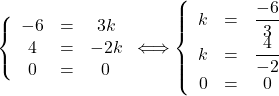
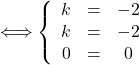 donc on a bien
donc on a bien ![]()
Donc ![]() et
et ![]() sont colinéaires
sont colinéaires
Donc ![]() et
et ![]() sont perpendiculaires
sont perpendiculaires
Exercices géométrie dans l’espace terminale D
Exercice sur la représentation paramétrique en terminale D
On considère les points ![]() ,
, ![]() , et
, et ![]() .
.
Donner une représentation paramétrique de la droite ![]() .
.
Exercice sur l’équation cartésienne du plan
Déterminer une équation cartésienne du plan ![]() défini par la condition suivante :
défini par la condition suivante :
Le projeté orthogonal de l’origine ![]() sur
sur ![]() est le point
est le point ![]() .
.
Corrigé des exercices géométrie dans l’espace
Corrigé de l’exercice représentation paramétrique
La droite ![]() est l’ensemble des points
est l’ensemble des points ![]() tels que:
tels que:
![Rendered by QuickLaTeX.com \[\exists k \in \mathbb{R}\text{, }\overrightarrow{AM}=k\overrightarrow{AB}=k\begin{pmatrix} -3 \\ 5 \\ 4 \\ \end{pmatrix}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-5622a946848ead6bdd05f6be64d83b4d_l3.png)
![Rendered by QuickLaTeX.com \[\Longleftrightarrow \exists k \in \mathbb{R}: \left \{ \begin{array}{c @{=} c} x - 2 = -3k \\ y + 3 = 5k \\ z = 4k \\ \end{array} \right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-efe64913f35ae72310a8a61be557030e_l3.png)
![Rendered by QuickLaTeX.com \[\Longleftrightarrow \exists k \in \mathbb{R}: \left \{ \begin{array}{c @{=} c} x = 2-3k \\ y = -3+5k \\ z = 4k \\ \end{array} \right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-da9a094bf7b0d056f24e7af31207d1b0_l3.png)
Corrigé de l’exercice sur l’équation cartésienne du plan en terminale D
Le vecteur 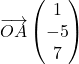 est normal au plan
est normal au plan ![]() . Une équation de
. Une équation de ![]() s’écrit donc:
s’écrit donc:
![]()
Le point ![]() appartient au plan
appartient au plan ![]() . Donc
. Donc ![]() .
.
Ainsi, une équation de ![]() est finalement:
est finalement:
![]()
Retrouvez d’autres exercices et corrigés des cours de maths niveau terminale D :
- Exercices corrigé gratuit : Fonction exponentielle
- Exercices corrigé gratuit : Equations différentielles
- Exercices corrigé gratuit : Statistiques
- Exercices corrigé gratuit : Exercices probabilité

