Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Avis Google France
★★★★★ 4,8 sur 5

Exercices sur les nombres réels, ensembles et intervalles en seconde

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Seconde Générale

Pour tout comprendre sur le cours en ligne des nombres réels, des ensembles et des intervalles, entaînez-vous avec les exercices suivants. Et retrouvez les autres exercices et corrigés en maths sur l’arithmétique, les fonctions affines et bien d’autres…

Exercices 1 : Nombres réels

1. Donner une définition formelle de l’ensemble des nombres décimaux $\mathbb{D}$ .

2. Démontrer que les nombres suivants sont dans $\mathbb{D}$ \ $\mathbb{Z}$ :

a) 12,52

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Exercice 2 : Nombres rationnels

1. Donner une définition formelle de l’ensemble des nombres rationnels $\mathbb{Q}$ .

2. Démontrer que les nombres suivants sont dans $\mathbb{Q}$ \ $\mathbb{D}$ :

a) $\dfrac {5}{3}$

b) $\dfrac {7}{11}$

Exercice 3 : Rationalité de racine de 2

On veut montrer par l’absurde que $\sqrt{2}$ n’est pas un élément de $\mathbb{Q}$ :

soit qu’il ne peut pas se mettre sous la forme $\dfrac {p}{q}$ avec $p$ $\in$ $\mathbb{Z}$ et $q$ $\in$ $\mathbb{Z}$ *.

On suppose qu’il existe deux entiers non nuls premiers entre eux $p$ et $q$ tel que $\sqrt{2}$ = $\dfrac {p}{q}$

1. Montrer que $2q²= p²$ .

2. En déduire que p est un nombre pair : $p = 2k$ pour un entier $k$ .

Exercice 4 : Diagramme de Venn

Dans la représentation en diagramme de Venn des ensembles de nombres suivants, placer deux nombres qui appartiennent à l’ensemble au-dessus mais n’appartiennent pas à la partie intérieure.

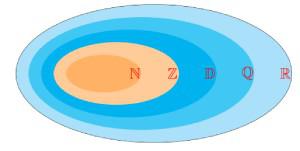
Corrigé exercices 1 : Nombres réels

1 – L’ensemble des nombre décimaux $\mathbb{D}$ est l’ensemble des nombres qu’on peut mettre sous la forme de $\dfrac {p}{10^k}$ avec $p$ $\in$ $\mathbb{Z}$ et $k$ $\in$ $\mathbb{N}$ .

2 – On note qu’un nombre $x$ $\in$ $\mathbb{D}$ \ $\mathbb{Z}$ si et seulement si $x$ $\in$ $\mathbb{D}$ et $x$ $\notin$ $\mathbb{Z}$

a) $\bullet$ 12,52 $\in$ $\mathbb{D}$ .

Par un raisonnement direct.

12,52 = 1252 x $10^{-2}$

12,52 = $\dfrac {1252}{10²}$

Donc, sous la forme $\dfrac {p}{10^k}$ ,

12,52 = $\dfrac {1252}{10²}$

avec $p$ = 1252 $\in$ $\mathbb{Z}$ et $k$ = 2 $\in$ $\mathbb{N}$

$\bullet$ 12,52 $\notin$ $\mathbb{Z}$ . Par l’absurde

On suppose que 12,52 $\in$ $\mathbb{Z}$ . Donc, il existe un entier relatif $p$ tel que $\dfrac {1252}{100}$ = $p$ . C’est-à-dire que 1252 =100 $\times p$ .

Ce qui montre que 1252 est divisible par 100.

Ce qui est absurde car un entier est divisible par100 si et seulement si son écriture décimale se termine par 00.

b) $\bullet$ $\dfrac {15}{4}$ $\in$ $\mathbb{D}$ Par un raisonnement direct.

$\dfrac {15}{4}$ = 3,75

$\dfrac {15}{4}$ = 375 x $10^{-2}$

$\dfrac {15}{4}$ = $\dfrac {375}{10^2}$

Donc, sous la forme $\dfrac {p}{10^k}$ , $\dfrac {15}{4}$ = $\dfrac {375}{10²}$ avec $p$ = 375 $\in$ $\mathbb{Z}$ et $k$ = 2 $\in$ $\mathbb{N}$ .

$\bullet$ $\dfrac {15}{4}$ $\notin$ $\mathbb{Z}$ . Par l’absurde.

On suppose que $\dfrac {15}{4}$ $\in$ $\mathbb{Z}$ .

Donc, il existe un entier relatif $p$ tel que $\dfrac {375}{100}$ = $p$ .

C’est-à-dire que 375 = 100 $\times$ $p$ . ce qui montre que 375 est divisible par 100.

Ce qui est absurde car un entier est divisible par 100 si et seulement si son écriture décimale se termine par 00.

Corrigé exercice 2 : Nombres rationnels

1 – L’ensemble des nombres rationnels $\mathbb{Q}$ est l’ensemble des nombres qui peut se mettre sous la forme $\dfrac {p}{q}$

avec p $\in$ $\mathbb{Z}$ et q $\in$ $\mathbb{N}^*$ .

2. a) On note qu’un nombre $x$ $\in$ $\mathbb{Q}$ \ $\mathbb{D}$ si et seulement si $x$ $\in$ $\mathbb{Q}$ et $x$ $\notin$ $\mathbb{D}$

$\bullet$ $\dfrac {5}{3}$ $\in$ $\mathbb{Q}$ . Par un raisonnement direct.

Le nombre $\dfrac {5}{3}$ est sous la forme $\dfrac {p}{q}$ avec p = 5 $\in$ $\mathbb{Z}$ et q = 3 $\in$ $\mathbb{N}^*$ .

Donc $\dfrac {5}{3}$ $\in$ $\mathbb{Q}$ .

$\bullet$ $\dfrac {5}{3}$ $\notin$ $\mathbb{D}$ . Par l’absurde.

On suppose que $\dfrac {5}{3}$ $\in$ $\mathbb{D}$ . Alors, il existe un entier $p$ et un entier naturel $k$ tel que $\dfrac {5}{3}$ = $\dfrac {p}{10^k}$ . Ce qui donne l’équivalence :

$\dfrac {5}{3}$ = $\dfrac {p}{10^k}$ $\iff$ 5 x $10^k$ = 3 $p$

Un entier est divisible par 3 si et seulement si la somme des nombres dans son écriture décimale est divisible par 3.

Mais la somme des nombres dans l’écriture décimale de 5 x $10^k$ est 5, ce qui n’est pas divisible par 3 alors l’égalité 5 x $10^k$ = 3 $p$ est impossible.

D’où la contradiction.

b) On note qu’un nombre $x$ $\in$ $\mathbb{Q}$ \ $\mathbb{D}$ si et seulement si $x$ $\in$ $\mathbb{Q}$ et $x$ $\notin$ $\mathbb{D}$

$\bullet$ $\dfrac {7}{11}$ $\in$ $\mathbb{Q}$ . Par un raisonnement direct.

Le nombre $\dfrac {7}{11}$ est sous la forme $\dfrac {p}{q}$ avec p = 7 $\in$ $\mathbb{Z}$ et q = 11 $\in$ $\mathbb{N}^*$ .

Donc $\dfrac {7}{11}$ $\in$ $\mathbb{Q}$ .

$\bullet$ $\dfrac {7}{11}$ $\notin$ $\mathbb{D}$ . Par l’absurde.

On suppose que $\dfrac {5}{3}$ $\in$ $\mathbb{D}$ . Alors, il existe un entier $p$ et un entier naturel $k$ tel que $\dfrac {7}{11}$ = $\dfrac {p}{10^k}$ . Ce qui donne l’équivalence :

$\dfrac {7}{11}$ = $\dfrac {p}{10^k}$ $\iff$ 7 x $10^k$ = 11 $p$

Un entier est divisible par 11 si et seulement si la différences entre les nombres de rangs impairs etles nombres de rangs pairs dans son écriture décimale est divisible par 11.

Comme la différence entre les nombres de rangs impairs et les nombres de rangs pairs de l’écriture décimale de 7 x $10^k$ est (7+ 0 + 0 + … +0) = 7,

ce qui n’est pas divisible par 11,

alors l’égalité 7 x $10^k$ = 11 $p$ est impossible.

D’où la contradiction.

Corrigé exercice 3 : Rationalité de racine de 2

1- On suppose qu’il existe deux entiers non nuls premiers entre eux $p$ et $q$ tels que $\sqrt{2}$ = $\dfrac {p}{q}$ avec $p$ $\in$ $\mathbb{Z}$ et

$p$ $\in$ $\mathbb{N}^*$ .

Par hypothèse, on a : $\sqrt{2}$ = $\dfrac {p}{q}$

$\sqrt{2}$ = $\dfrac {p}{q}$ $\iff$ $q$ $\sqrt{2}$ = $p$

$\sqrt{2}$ = $\dfrac {p}{q}$ $\iff$ 2 $q²$ = $p²~$ (on passe au carré)

Ce qui donne 2 $q²$ = $p²$ , c’est-à-dire que $p²$ est un nombre pair.

Comme un entier est pair si et seulement si son carré est pair, alors $p$ est un nombre pair.

Donc il existe k tel que $p = 2k$ .

2 – D’après la question précédente :

2 $q²$ = $p²$ et $p = 2k$ pour un entier $k$ .

Donc

2 $q²$ = $p²$ $\iff$ 2 $q²$ = $(2k)²$

2 $q²$ = $p²$ $\iff$ 2 $q²$ = $4k²$

2 $q²$ = $p²$ $\iff$ $q²$ = $2k²$

Avec le même raisonnement que précédemment, $q²$ est un nombre pair. Donc $q$ est un nombre pair.

Par conséquent, 2 est un diviseur commun de $p$ et de $q$ .

Ce qui contredit l’hypothèse selon laquelle $p$ et $q$ sont premiers entre eux.

En conclusion, $\sqrt{2}$ $\notin$ $\mathbb{Q}$ car $\sqrt{2}$ ne peut pas se mettre sous la forme $\dfrac {p}{q}$ avec $p$ $\in$ $\mathbb{Z}$ et $p$ $\in$ $\mathbb{N}^*$ .

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Corrigé exercice 4 : Diagramme de Venn

Dans $\mathbb{N}$ : 1 et 2020 par exemple

Dans $\mathbb{Z}$ : -200 et -2 par exemple

Dans $\mathbb{D}$ : -19,75 et 1,5 par exemple

Dans $\mathbb{Q}$ : – $\dfrac {73}{7}$ et $\dfrac {143}{3}$ par exemple

Dans $\mathbb{R}$ : – $\sqrt{2}$ et $\sqrt{3}$ par exemple

Retrouvez d’autres cours en ligne de maths seconde sur notre site :