Mon parcours pour réussir en maths
J'aprends le cours par coeur
Je travaille avec un prof de maths
Je travaille entre chaque séance
Avis Google France
★★★★★ 4,8 sur 5
Fonction affine en seconde générale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Seconde générale
Ce cours en ligne de maths en seconde générale permet aux élèves de réviser le chapitre de la fonction affine. Un professeur particulier de maths vous offre aussi l’opportunité de progresser sur les fonctions affine en seconde.
Ce chapitre fait partie des incontournables du programme de seconde avec d’autres chapitres tels que l’arithmétique, les généralités et variations de fonction, etc.
Fonction affine : définition
Une fonction f est une fonction affine si, pour tout réel ![]() ,
,
![]() ,
, ![]() ,
, ![]()
Une fonction affine est représentée dans un repère par une droite.
![]() est donc le coefficient directeur de la droite représentative de la fonction, et
est donc le coefficient directeur de la droite représentative de la fonction, et ![]() est l’ordonnée à l’origine, c’est-à-dire l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées.
est l’ordonnée à l’origine, c’est-à-dire l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Signe d’une fonction affine
- Propriété
Soit ![]() , où
, où ![]() .
.
![]() Si
Si ![]() alors le signe de
alors le signe de ![]() est donné par le tableau suivant :
est donné par le tableau suivant :

![]() Si
Si ![]() alors le signe de
alors le signe de ![]() est donné par le tableau suivant :
est donné par le tableau suivant :

Et si ![]() , la fonction est croissante :
, la fonction est croissante :
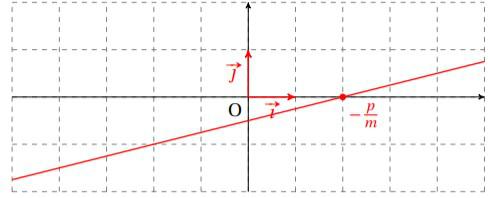
La droite est au-dessus de l’axe des abscisses pour ![]() , ce qui signifie que
, ce qui signifie que ![]() sur
sur ![]() et donc :
et donc :
![]() sur
sur ![]()
d’où le tableau de signes :

Fonction affine et linéaire
- Définition d’une fonction affine linéaire
Une fonction ![]() est une fonction linéaire si pour tout réel
est une fonction linéaire si pour tout réel ![]() ,
, ![]() ,
, ![]() .
.
C’est un cas particulier de fonctions affines. La représentation graphique d’une fonction linéaire est une droite passant par l’origine du repère.
- Propriété d’une fonction affine linéaire
Soit ![]() , avec
, avec ![]() .
.
![]() Si
Si ![]() alors le signe de
alors le signe de ![]() est donné par le tableau suivant :
est donné par le tableau suivant :

![]() Si
Si ![]() alors le signe de
alors le signe de ![]() est donné par le tableau suivant :
est donné par le tableau suivant :

Fonction affine linéaire : équations-produits
- Définition
Une équation-produit (sous-entendu équation-produit nul) est une équation dont un membre est le produit de plusieurs fonctions affines ou linéaires et dont le second membre est le nombre 0.
-
- Exemple :
Soit ![]() une équation. Cette équation est-elle une équation produit ?
une équation. Cette équation est-elle une équation produit ?
Le membre de gauche est le produit des fonctions affines ![]() et
et ![]() .
.
- Théorème
Un produit est nul si et seulement si l’un de ses facteurs est nul.
-
- Exemple :
![]() ou
ou ![]()
![]() ou
ou ![]()
![]() ou
ou ![]()
L’ensemble de solution de l’équation ![]() est donc S =
est donc S = ![]() .
.
Fonction affine linéaire : inéquations-produits
- Définition
Une inéquation-produit (sous-entendu inéquation-produit nul) est une inéquation dont un membre est le produit de plusieurs fonctions affines ou linéaires et dont le second membre est le nombre 0.
-
- Exemple :
On souhaite résoudre l’inéquation :
![]()
![]() on cherche le signe de chaque facteur.
on cherche le signe de chaque facteur.
Soit ![]() .
.
Cette équation correspond à quelle proposition parmi les suivantes :
a) ![]()
b) ![]()
c) ![]()
d) ![]()
-
- Solution
![]()
![]()
De même,
![]()
![]()
![]() on en déduit le tableau de signe
on en déduit le tableau de signe
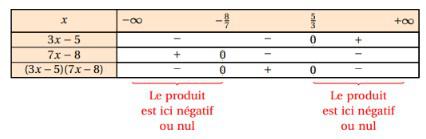
Donc l’ensemble solution de l’inéquation est :
S = ![]()
![]()
![]()
Fonction affine linéaire : inéquations-quotients
- Définition
Une inéquation-quotient est une inéquation où un membre est de la forme ![]() , où
, où ![]() et
et ![]() sont des produits de fonctions affines.
sont des produits de fonctions affines.
-
- Exemple
![]() est une inéquation – quotient.
est une inéquation – quotient.
Pour résoudre une inéquation-quotient, on procède de la même façon que pour les inéquations-produits, à ceci près que l’on doit toujours exclure sur la dernière ligne du tableau de signes les valeurs de x qui annulent le dénominateur.
Cela se traduit par des doubles barres, symbolisées par « || », au niveau des valeurs de x à exclure.
-
- Exemple de résolution
On souhaite résoudre l’inéquation :
![]()
Sous quel nombre y aura-t-il des doubles barres dans le tableau de signes ?
a) -2
b) 3
c) 2
d) 4
Les doubles barres symbolisent une valeur impossible, qui annule le dénominateur. Or cette valeur est -2. Cela se trouve facilement avec une résolution d’équation comme vu plus haut.
L’ensemble solution de l’inéquation est donc : S = ![]()
Ce cours sur la fonction affine en seconde est aussi disponible sur l’application mobile PrepApp.
Retrouvez d’autres cours en ligne de maths seconde sur notre site :

