Chapitres de maths en Terminale D
Cours sur les limites, continuité et dérivabilité en Terminale D
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale D
Vous trouverez ci-dessous un cours de maths sur les limites, continuité et dérivabilité proposé aux élèves de terminale D.
1. Cours sur la continuité en terminale D
Continuité en un point
Définition : Une fonction ![]() est continue en un réel
est continue en un réel ![]() si et seulement si
si et seulement si ![]() .
.
Propriétés : Les polynômes, les fonctions rationnelles (quotient de polynômes), les fonctions trigonométriques, la fonction racine carrée, la fonction valeur absolue sont continues sur leur ensemble de définition.
Définition : fonction partie entière
Pour tout réel ![]() , la partie entière de
, la partie entière de ![]() , notée
, notée ![]() , est l’unique entier relatif vérifiant :
, est l’unique entier relatif vérifiant :
![]()
Remarque : la fonction partie entière est une fonction en escalier. En effet, elle est constante sur chaque intervalle ouvert ![]() , avec
, avec ![]() :
:
![]() ,
, ![]()

Continuité sur un intervalle
Définition : Une fonction ![]() est continue sur un intervalle
est continue sur un intervalle ![]() si et seulement si elle est continue en tout point
si et seulement si elle est continue en tout point ![]() de
de ![]() .
.
Théorème des valeurs intermédiaires : Soit ![]() une fonction continue sur un intervalle
une fonction continue sur un intervalle ![]() ,
, ![]() et
et ![]() deux réels de
deux réels de ![]() .
.
Pour tout réel ![]() compris entre
compris entre ![]() et
et ![]() , il existe un réel
, il existe un réel ![]() compris entre
compris entre ![]() et
et ![]() tel que
tel que ![]() .
.
![]() ,
, ![]() ,
,
![]()
Corollaire :
Si ![]() est continue sur
est continue sur ![]() et si
et si ![]() alors
alors ![]() s’annule en un réel de
s’annule en un réel de ![]() .
.
Si ![]() est une fonction continue et strictement monotone sur
est une fonction continue et strictement monotone sur ![]() ,
,
alors ![]() , l’équation
, l’équation ![]() admet une unique solution dans
admet une unique solution dans ![]() .
.
Si ![]() est continue et strictement monotone sur
est continue et strictement monotone sur ![]() et si
et si ![]() ,
,
alors l’équation ![]() admet une unique solution dans
admet une unique solution dans ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2 – Résumé de cours sur la dérivation en terminale D
Taux d’accroissement
Définition : Soit f une fonction définie sur un intervalle ![]() contenant deux réels distincts
contenant deux réels distincts ![]() et
et ![]() .
.
On appelle taux d’accroissement (ou taux de variation) de la fonction ![]() entre
entre ![]() et
et ![]() le réel :
le réel :
![]()
Nombre dérivé et tangente
Définition : dérivabilité en un point
Soit ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() contenant un réel
contenant un réel ![]() . On dit que
. On dit que ![]() est dérivable en
est dérivable en ![]() si et seulement si
si et seulement si
![]() existe et est finie.
existe et est finie.
Dans ce cas, on note :
![]()
Le réel ![]() ainsi défini est appelé nombre dérivé de
ainsi défini est appelé nombre dérivé de ![]() en
en ![]() .
.
Définition : dérivabilité sur un intervalle
Une fonction ![]() est dite dérivable sur un intervalle
est dite dérivable sur un intervalle ![]() si elle est dérivable en tout réel de
si elle est dérivable en tout réel de ![]() .
.
La fonction qui a tout réel ![]() de
de ![]() associe son nombre dérivé en
associe son nombre dérivé en ![]() est appelée fonction dérivée de
est appelée fonction dérivée de ![]() et est notée
et est notée ![]() .
.
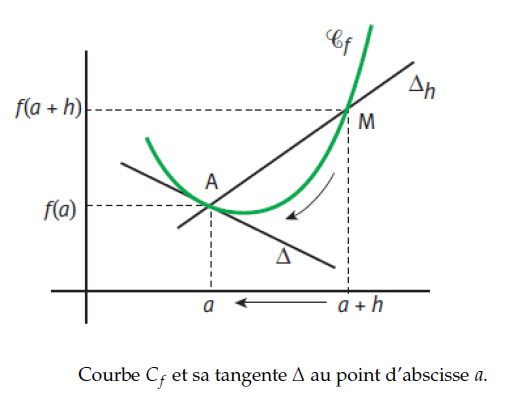
Propriété : équation de la tangente en un point
Soit ![]() une fonction dérivable sur un intervalle I contenant un réel
une fonction dérivable sur un intervalle I contenant un réel ![]() et
et ![]() sa courbe représentative.
sa courbe représentative.
La courbe ![]() admet au point de coordonnées
admet au point de coordonnées ![]() une tangente d’équation :
une tangente d’équation :
![]() :
: ![]()
Théorème : dérivée et variations
Soit ![]() une fonction définie et dérivable sur un intervalle
une fonction définie et dérivable sur un intervalle ![]() .
.
La fonction ![]() est croissante sur
est croissante sur ![]() si et seulement si
si et seulement si ![]() .
.
La fonction ![]() est décroissante sur
est décroissante sur ![]() si et seulement si
si et seulement si ![]() .
.
La fonction ![]() est constante sur
est constante sur ![]() si et seulement si
si et seulement si ![]() .
.
Corollaire
Soit ![]() une fonction définie et dérivable sur un intervalle
une fonction définie et dérivable sur un intervalle ![]() contenant un réel
contenant un réel ![]() .
.
Si ![]() admet un extremum local en
admet un extremum local en ![]() alors
alors ![]() .
.
Si ![]() s’annule en
s’annule en ![]() en changeant de signe alors
en changeant de signe alors ![]() admet un extremum local en
admet un extremum local en ![]() .
.
Théorème
La fonction ![]() est strictement croissante sur un intervalle
est strictement croissante sur un intervalle ![]() si et seulement si
si et seulement si
![]() est strictement positive sur
est strictement positive sur ![]() sauf éventuellement en des réels isolés où elle s’annule.
sauf éventuellement en des réels isolés où elle s’annule.
La fonction ![]() est strictement décroissante sur un intervalle
est strictement décroissante sur un intervalle ![]() si et seulement si
si et seulement si
![]() est strictement négative sur
est strictement négative sur ![]() sauf éventuellement en des réels isolés où elle s’annule.
sauf éventuellement en des réels isolés où elle s’annule.
Formulaire des dérivées en terminale D

Dérivée et opérations en terminale D
Soient ![]() et
et ![]() deux fonctions dérivables sur un intervalle
deux fonctions dérivables sur un intervalle ![]() . Soit
. Soit ![]() .
.

Variations
Définition :
La fonction ![]() est croissante sur un intervalle
est croissante sur un intervalle ![]() si et seulement si,
si et seulement si,
pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
La fonction ![]() est strictement croissante sur un intervalle
est strictement croissante sur un intervalle ![]() si et seulement si,
si et seulement si,
pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
La fonction ![]() est décroissante sur un intervalle
est décroissante sur un intervalle ![]() si et seulement si,
si et seulement si,
pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
La fonction ![]() est strictement décroissante sur un intervalle
est strictement décroissante sur un intervalle ![]() si et seulement si,
si et seulement si,
pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
Propriété : signe d’une fonction affine
Une fonction affine ![]() définie sur
définie sur ![]() s’écrit :
s’écrit :
![]() ,
, ![]() , où
, où ![]() est le coefficient directeur de la droite, et
est le coefficient directeur de la droite, et ![]() son ordonnée à l’origine.
son ordonnée à l’origine.
Pour l’étude du signe, la valeur importante est l’abscisse ![]() qui annule la fonction
qui annule la fonction ![]() :
:
![]()
si ![]() , alors
, alors ![]() est croissante. Donc
est croissante. Donc ![]() est négative sur
est négative sur ![]() , puis positive sur
, puis positive sur ![]() .
.
si ![]() , alors
, alors ![]() est décroissante. Donc
est décroissante. Donc ![]() est positive sur
est positive sur ![]() , puis négative sur
, puis négative sur ![]() .
.
Propriété : signe d’un polynôme du second degré
Soit ![]() et
et ![]() une fonction polynôme de degré 2. Pour l’étude du signe de
une fonction polynôme de degré 2. Pour l’étude du signe de ![]() , deux cas de figure se présentent :
, deux cas de figure se présentent :
Si ![]() , alors
, alors ![]() est de signe constant, et prend le signe de
est de signe constant, et prend le signe de ![]() .
.
Si ![]() , alors
, alors ![]() possède deux racines réelles et change de signe.
possède deux racines réelles et change de signe.
La fonction ![]() prend le signe opposé de
prend le signe opposé de ![]() entre les racines
entre les racines
![]() et
et ![]() , c’est-à-dire sur
, c’est-à-dire sur ![]() , et le signe de
, et le signe de ![]() à l’extérieur des racines, sur
à l’extérieur des racines, sur ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3 – Composée de fonctions en terminale D
Lorsque l’on enchaîne une fonction u suivie d’une fonction v, on définit une fonction ![]() appelée composée de
appelée composée de ![]() par
par ![]() .
.
La fonction ![]() ainsi définie est notée
ainsi définie est notée ![]() . On lit « u rond v ».
. On lit « u rond v ».
Dire que ![]() signifie donc que pour tout
signifie donc que pour tout ![]() de l’ensemble de définition de
de l’ensemble de définition de ![]() , on a
, on a ![]() .
.
Soient ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() et
et ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() tel que
tel que ![]() .
.
La situation peut être résumée par le schéma suivant :
![]()
Dérivée d’une fonction composée
Soit ![]() une fonction composée, définie sur
une fonction composée, définie sur ![]() par :
par : ![]() .
.
Si :
 est dérivable sur
est dérivable sur 
 est dérivable sur
est dérivable sur 
 ,
, 
Alors la composée ![]() est dérivable sur
est dérivable sur ![]() et
et
![]() ,
, ![]()
4. Limites de fonctions en terminale D
Limite en 
Limite en ![]()
Soit ![]() une fonction définie au voisinage de
une fonction définie au voisinage de ![]() , c’est-à-dire sur un intervalle du type
, c’est-à-dire sur un intervalle du type ![]() :
:
![]() tend vers
tend vers ![]() lorsque
lorsque ![]() tend vers
tend vers ![]() si tout intervalle ouvert contenant
si tout intervalle ouvert contenant ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() suffisamment grand. On note alors :
suffisamment grand. On note alors :
![]()
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() suffisamment grand. On note alors :
suffisamment grand. On note alors :
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() suffisamment grand. On note alors :
suffisamment grand. On note alors :
![]()
Limite en 
Soit ![]() une fonction définie au voisinage de
une fonction définie au voisinage de ![]() , c’est-à-dire sur un intervalle du type
, c’est-à-dire sur un intervalle du type ![]() :
:
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle ouvert contenant
si tout intervalle ouvert contenant ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() négatif, suffisamment grand en valeur absolue. On note alors :
négatif, suffisamment grand en valeur absolue. On note alors :
![]()
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() négatif, suffisamment grand en valeur absolue. On note alors :
négatif, suffisamment grand en valeur absolue. On note alors :
![]()
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() négatif, suffisamment grand en valeur absolue. On note alors :
négatif, suffisamment grand en valeur absolue. On note alors :
![]()
Propriétés : limites de fonctions usuelles
![]()
![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
Opérations sur les limites en terminale D
Somme de limites : ![]()
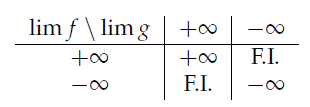
Produit de limites : ![]()
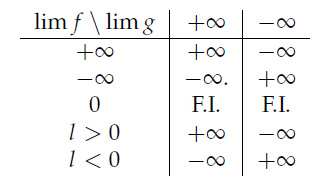
Retrouvez d’autres chapitres à travailler en cours de maths en terminale D :
- Cours en ligne raisonnement par récurrence terminale D
- Suites numériques terminale D
- Cours sur la fonction Logarithme en terminale D
- Terminale D : Nombres complexes et géométrie

