Chapitres de maths en Terminale S2
Cours sur les limites et dérivabilité en Terminale S2
Résumé de cours Exercices et corrigés
Cours en ligne de maths en Terminale S2
Ce résumé de cours contenant toutes les notions au programme de terminale S2 propose de travailler sur les notions de limite et de dérivabilité des fonctions. Ce cours de mathématiques peut aider à préparer le bac et les études supérieures.
1. Résumé de cours sur la continuité en terminale S2
Continuité en un point
Une fonction ![]() est dite continue au voisinage d’un réel
est dite continue au voisinage d’un réel ![]() si et seulement si
si et seulement si ![]() .
.
Ainsi, les fonctions polynômes, rationnelles, trigonométriques et la fonction racine carrée sont continues sur leur ensemble de définition.
Continuité sur I, un intervalle de l’ensemble de définition
Une fonction ![]() est dite continue sur un intervalle
est dite continue sur un intervalle ![]() de son ensemble de définition si et seulement si elle est continue en tout point
de son ensemble de définition si et seulement si elle est continue en tout point ![]() de cet intervalle.
de cet intervalle.
Théorème des valeurs intermédiaires (TVI) : Soit ![]() une fonction continue sur un intervalle
une fonction continue sur un intervalle ![]() ,
, ![]() et
et ![]() deux réels de
deux réels de ![]() .
.
Pour tout réel ![]() compris entre
compris entre ![]() et
et ![]() , il existe un réel
, il existe un réel ![]() compris entre
compris entre ![]() et
et ![]() tel que
tel que ![]() .
.
![]() ,
, ![]() ,
,
![]()
Corollaire du Théorème des valeurs intermédiaire en terminale S2 :
Si une fonction ![]() est continue sur
est continue sur ![]() et si
et si ![]() alors
alors ![]() s’annule en un réel de
s’annule en un réel de ![]() .
.
Si ![]() est une fonction continue et strictement monotone sur
est une fonction continue et strictement monotone sur ![]() ,
,
alors ![]() , l’équation
, l’équation ![]() admet une unique solution dans
admet une unique solution dans ![]() .
.
Si ![]() est continue et strictement monotone sur
est continue et strictement monotone sur ![]() et si
et si ![]() ,
,
alors l’équation ![]() admet une unique solution dans
admet une unique solution dans ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2 – Dérivabilité en terminale S2
Taux de variation d’une fonction en terminale S2
Soit g une fonction définie sur un intervalle ![]() contenant deux réels distincts
contenant deux réels distincts ![]() et
et ![]() .
.
On appelle taux de variation (ou taux d’accroissement) de la fonction ![]() entre
entre ![]() et
et ![]() le réel :
le réel :
![]()
Équation de tangente et nombre dérivé
Dérivabilité en un point
Soit ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() contenant un réel
contenant un réel ![]() . On dit que
. On dit que ![]() est dérivable en
est dérivable en ![]() si et seulement si
si et seulement si
![]() existe et est finie.
existe et est finie.
On note alors :
![]()
Le réel ![]() ainsi défini est appelé nombre dérivé de
ainsi défini est appelé nombre dérivé de ![]() en
en ![]() .
.
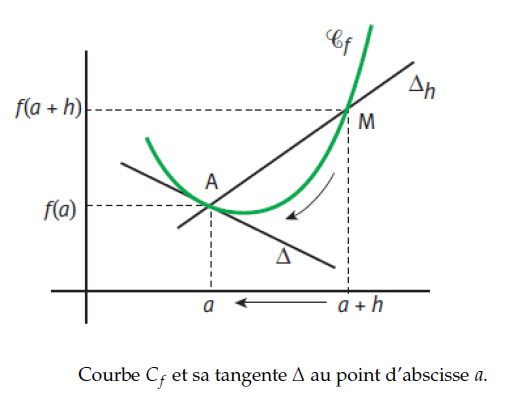
Dérivabilité sur un intervalle
Une fonction ![]() est dite dérivable sur un intervalle
est dite dérivable sur un intervalle ![]() si elle est dérivable en tout réel de
si elle est dérivable en tout réel de ![]() .
.
La fonction qui a tout réel ![]() de
de ![]() associe son nombre dérivé en
associe son nombre dérivé en ![]() est appelée fonction dérivée de
est appelée fonction dérivée de ![]() et est notée
et est notée ![]() .
.
Équation de la tangente en un point
Soit ![]() une fonction dérivable sur un intervalle I contenant un réel
une fonction dérivable sur un intervalle I contenant un réel ![]() et
et ![]() sa courbe représentative.
sa courbe représentative.
La courbe ![]() admet au point de coordonnées
admet au point de coordonnées ![]() une tangente d’équation :
une tangente d’équation :
![]() :
: ![]()
Dérivation et variations
Soit ![]() une fonction définie et dérivable sur un intervalle
une fonction définie et dérivable sur un intervalle ![]() .
.
La fonction ![]() est croissante sur
est croissante sur ![]() si et seulement si
si et seulement si ![]() ,
, ![]() .
.
La fonction ![]() est décroissante sur
est décroissante sur ![]() si et seulement si
si et seulement si ![]() ,
, ![]() .
.
La fonction ![]() est constante sur
est constante sur ![]() si et seulement si
si et seulement si ![]() ,
, ![]() .
.
Corollaire sur la dérivation et variation
Soit ![]() une fonction définie et dérivable sur un intervalle
une fonction définie et dérivable sur un intervalle ![]() contenant un réel
contenant un réel ![]() .
.
Si ![]() admet un extremum local en
admet un extremum local en ![]() alors
alors ![]() .
.
Si ![]() s’annule en
s’annule en ![]() en changeant de signe alors
en changeant de signe alors ![]() admet un extremum local en
admet un extremum local en ![]() .
.
Théorème
La fonction ![]() est strictement croissante sur un intervalle
est strictement croissante sur un intervalle ![]() si et seulement si
si et seulement si
![]() est strictement positive sur
est strictement positive sur ![]() sauf éventuellement en des réels isolés où elle s’annule.
sauf éventuellement en des réels isolés où elle s’annule.
La fonction ![]() est strictement décroissante sur un intervalle
est strictement décroissante sur un intervalle ![]() si et seulement si
si et seulement si
![]() est strictement négative sur
est strictement négative sur ![]() sauf éventuellement en des réels isolés où elle s’annule.
sauf éventuellement en des réels isolés où elle s’annule.
Formules de dérivées en terminale S2

Dérivée et opérations en terminale S2
Soient deux fonctions ![]() et
et ![]() dérivables sur un intervalle
dérivables sur un intervalle ![]() . Soit
. Soit ![]() .
.

Variations de fonctions en terminale S2
Définition :
La fonction ![]() est croissante sur un intervalle
est croissante sur un intervalle ![]() si et seulement si,
si et seulement si,
pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
La fonction ![]() est strictement croissante sur un intervalle
est strictement croissante sur un intervalle ![]() si et seulement si,
si et seulement si,
Pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
La fonction ![]() est décroissante sur un intervalle
est décroissante sur un intervalle ![]() si et seulement si,
si et seulement si,
pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
La fonction ![]() est strictement décroissante sur un intervalle
est strictement décroissante sur un intervalle ![]() si et seulement si,
si et seulement si,
Pour tous réels ![]() et
et ![]() de
de ![]() tels que
tels que ![]() , on a
, on a ![]() .
.
Propriété : signe d’une fonction affine
Une fonction affine ![]() définie sur
définie sur ![]() s’écrit :
s’écrit :
![]() ,
, ![]() , où
, où ![]() est le coefficient directeur de la droite, et
est le coefficient directeur de la droite, et ![]() son ordonnée à l’origine.
son ordonnée à l’origine.
![]()
si ![]() , alors
, alors ![]() est croissante. Donc
est croissante. Donc ![]() est négative sur
est négative sur ![]() , puis positive sur
, puis positive sur ![]() .
.
si ![]() , alors
, alors ![]() est décroissante. Donc
est décroissante. Donc ![]() est positive sur
est positive sur ![]() , puis négative sur
, puis négative sur ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3 – Composée de fonctions en terminale S2
Lorsque l’on applique une fonction à une autre fonction, on définit une fonction ![]() appelée composée de
appelée composée de ![]() par
par ![]() .
.
La fonction ![]() ainsi définie est notée
ainsi définie est notée ![]() . On dit que g est « u rond v ».
. On dit que g est « u rond v ».
Dire que ![]() signifie donc que pour tout
signifie donc que pour tout ![]() de l’ensemble de définition de
de l’ensemble de définition de ![]() , on a
, on a ![]() .
.
Soient ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() et
et ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() tel que
tel que ![]() .
.
La situation peut être résumée par le schéma suivant :
![]()
Dérivation d’une fonction composée terminale S2
Soit ![]() une fonction composée, définie sur
une fonction composée, définie sur ![]() par :
par : ![]() ,
, ![]() .
.
Si :
 est dérivable sur
est dérivable sur 
 est dérivable sur
est dérivable sur 
 ,
, 
Alors la composée ![]() est dérivable sur
est dérivable sur ![]() et
et
![]() ,
, ![]()
4. Limites de fonctions en terminale S2
Limite des fonctions en 
Limite en ![]()
Soit ![]() une fonction définie au voisinage de
une fonction définie au voisinage de ![]() , c’est-à-dire sur un intervalle du type
, c’est-à-dire sur un intervalle du type ![]() :
:
![]() tend vers
tend vers ![]() lorsque
lorsque ![]() tend vers
tend vers ![]() si tout intervalle ouvert contenant
si tout intervalle ouvert contenant ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() suffisamment grand. On note alors :
suffisamment grand. On note alors :
![]()
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() suffisamment grand. On note alors :
suffisamment grand. On note alors :
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() suffisamment grand. On note alors :
suffisamment grand. On note alors :
![]()
Limite en 
Soit ![]() une fonction définie au voisinage de
une fonction définie au voisinage de ![]() , c’est-à-dire sur un intervalle du type
, c’est-à-dire sur un intervalle du type ![]() :
:
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle ouvert contenant
si tout intervalle ouvert contenant ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() négatif, suffisamment grand en valeur absolue. On note alors :
négatif, suffisamment grand en valeur absolue. On note alors :
![]()
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() négatif, suffisamment grand en valeur absolue. On note alors :
négatif, suffisamment grand en valeur absolue. On note alors :
![]()
![]() tend vers
tend vers ![]() lorsque x tend vers
lorsque x tend vers ![]() si tout intervalle du type
si tout intervalle du type ![]() contient toutes les valeurs de
contient toutes les valeurs de ![]() pour
pour ![]() négatif, suffisamment grand en valeur absolue. On note alors :
négatif, suffisamment grand en valeur absolue. On note alors :
![]()
Opérations sur les limites de fonctions en terminale S2
Somme de limites de fonctions : ![]()
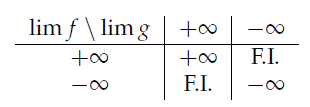
Produit de limites de fonctions : ![]()
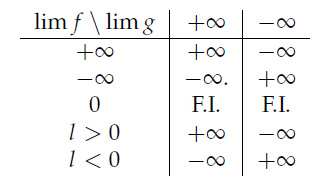
N’hésitez pas à consulter nos autres notions pour progresser en maths en terminale S2 :
- Résumé de cours sur les suites en terminale S2
- Fonction logarithme en terminale S2
- Terminale D : Nombres complexes et géométrie

