Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Exemple de colle de physique en prépa scientifique pour s’entraîner

Les interrogations orales de physique en prépa ou khôlle de physique sont légion en cours de prépa scientifique. C’est aussi ce format que vous rencontrerez aux concours CPGE durant les épreuves orales. Il faut donc s’y préparer comme tout autre oral (par exemple oral de français en prépa). Les 5/2 auront à cœur de travailler dès le début d’année sur des annales de concours d’ingénieur ou sur des colles de physique tombées aux concours pour intégrer Polytechnique. Pour un début d’entraînement vous trouverez ci-dessous 2 exemples de colle de physique pour les élèves de cours maths spé. D’autres exemples suivront si vous nous le demandez 😜 en commentaire tout en bas ! Aussi n’oubliez pas notre app mobile gratuite en maths pour les maths spé 🙂 un précieux compagnon jusqu’aux concours !

STAGE INTENSIF EN PRÉPA SCIENTIFIQUE

Profite de tes vacances pour progresser en vue des concours.

96% de réussite aux concours
44% dans le TOP 10
99% de recommandation

Avis Google France ★★★★★ 4,9 sur 5

Exercice 1 : khôlle de physique optique, un grand classique

On dispose d’un banc optique sur lequel sont alignés, dans l’ordre, un objet réel $\overline{AB}$ , une lentille de distance focale $f^\prime$ en $O$ et un écran sur lequel on forme l’image $\overline{A^\prime B^\prime}$ . On note $D$ la distance séparant l’objet de son image. Quelle est la condition sur $D$ pour qu’un objet réel done une image réelle ?

Prologue : cet exercice est un classique. Il est souvent traité en cours de physique, mais pas toujours. Il n’y a pas de difficulté particulière, donc il permet d’évaluer la maîtrise du cours par l’étudiant, ainsi que sa compréhension de l’optique.

1) On commence l’exercice en faisant un $\textbf{sch\'ema}$ comportant les éléments suivants :

l’axe optique
les conventions pour les longueurs et les angles
l’objet réel, la lentille et l’écran, et faire apparaître la distance $D$ .

2) Un objet est réel ssi $\overline{AO}>0$ , et son image est réelle ssi $\overline{OA^{\prime}}>0$ .

3) La relation de conjugaison pour une lentille convergente s’écrit :

$\dfrac{1}{\overline{OA^{\prime}}} - \dfrac{1}{\overline{OA}} = \dfrac{1}{f^{\prime}}$

4) On cherche une condition sur $D$ telle que $\overline{OA^{\prime}}>0$ . On fait apparaître $D$ en utilisant $D = \overline{AO}+\overline{OA^{\prime}}$ (les longueurs sont algébriques), ce qui élimine $\overline{AO}$ , puis on réarrange l’expression pour obtenir :

$\overline{OA^{\prime}}^2 - D \overline{OA^{\prime}} + Df^{\prime} = 0$

C’est un polynôme d’ordre 2 à coefficients réels dont le discriminant est $\Delta = D\left(D-4f^{\prime}\right)$ .

5) Si $\Delta<0$ ( $D<4f^{\prime}$ ), il n’y a pas d’image du tout. Cela veut dire qu’en fixant une distance $D<4f^{\prime}$ on ne peut pas déplacer le système objet+écran jusqu’à avoir une image $\overline{A^\prime B^\prime}$ nette sur l’écran (peu importe si l’image et l’objet soient réels ou virtuels !).

Si $\Delta>0$ ( $D>4f^{\prime}$ ), il est possible de déplacer le système objet+écran et trouver $\textbf{deux}$ positions telles que l’image $\overline{A^\prime B^\prime}$ soit nette sur l’écran. Les deux positions sont déterminées par les racines du polynôme :

$\overline{OA^{\prime}} = \frac{1}{2}\left(D \pm \sqrt{D(D-4f^{\prime})}\right)$

On constate alors que la solution avec un + donne bien $\overline{OA^{\prime}}>0$ . La condition nécessaire est donc $\boxed{D \geq 4 f^{\prime}}$ .

Le cas limite $D=4f^{\prime}$ donne $\overline{OA^{\prime}} = \frac{D}{2} = 2f^{\prime}$ . Autrement dit, l’objet à $2f^{\prime}$ avant la lentille, et l’écran à $2f^{\prime}$ après la lentille.

Épilogue : cet exercice est facile et ne doit pas prendre plus de 30 minutes à faire. La difficulté est d’expliquer $\textbf{pourquoi}$ on cherche les racines du polynôme et pourquoi le signe du discriminant est important. Il a une importance cruciale en TP : une lentille de distance focale $f=1$ m nécessite au minimum 4 m entre l’objet et l’écran, ce qui est très encombrant…}

STAGE INTENSIF EN PRÉPA SCIENTIFIQUE

Profite de tes vacances pour progresser en vue des concours.

96% de réussite aux concours
44% dans le TOP 10
99% de recommandation

Avis Google France ★★★★★ 4,9 sur 5

Exercice 2 (d’après Centrale PSI 2016) : colle de physique en mécanique des fluides

On souhaite mesurer la viscosité $\eta$ de l’eau à l’aide du dispositif suivant :

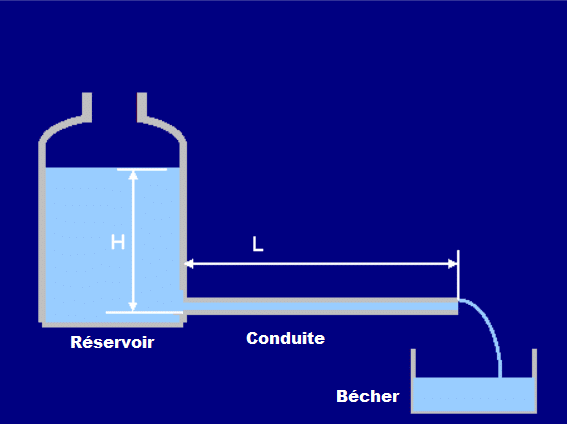
Dans la conduite, la vitesse est de la forme $v(M) = \frac{\Delta P}{4 \eta L} \left(a^2-r^2\right)$ , où $r$ est la position (distance au centre de la conduite), $a=2.5$ mm est le rayon de la conduite, $L=30$ cm sa longueur et $\Delta P$ la différence de pression entre les deux extrémités.
$\bullet$ Calculer $\Delta P$ , sachant que $H=20$ cm et reste quasi-constant.
$\bullet$ Calculer le débit massique $D_m$ en sortie de la conduite.
$\bullet$ On obtient 320 g de solution en 30 s. En déduire $\eta$ .
$\bullet$ Quel est le type d’écoulement dans la conduite ?

Prologue : pas de temps de préparation, l’étudiant passe directement au tableau. L’exercice étant un classique de mécanique des fluides (écoulement de Poiseuille), il est « plus facile » mais l’examinateur pardonnera moins les erreurs et oublis du cours.

COURS PARTICULIERS DE PHYSIQUE

Nous avons recruté pour vous les meilleurs profs de physique.

POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES

Avis Google France ★★★★★ 4,9 sur 5

0) Dans tout exercice il est utile de définir des points fictifs pour désigner les points dont on parle. On définit alors :

$\bullet$ A le point à la surface de l’eau se trouvant dans le réservoir
$\bullet$ B le point entre le réservoir et la conduite
$\bullet$ C le point à la sortie du conduite.

1) La pression étant une grandeur continue, au point A la pression est celle de l’atmosphère. Comme $H$ varie peu, il faut comprendre qu’on se place dans le cas $\textbf{statique dans le r\'eservoir uniquement}$ (entre A et B). La pression se calcule alors avec l’équation de l’hydrostatique des fluides : $\vec{grad} P = -\rho g$ ; qui après intégration donne $\Delta P = P_B - P_A = \rho g H$ . L’application numérique donne $\Delta P = 2\times 10^3$ Pa.

2) Le profil des vitesses étant donné, on utilise la définition du débit massique :

$D_m = \int_{\text{Section de la conduite}} \rho v dS$

Attention : comme la vitesse $v$ varie avec la position dans la conduite, l’intégrale doit être faite $\textbf{proprement}$ . Pour cela :

$\bullet$ dire à l’oral qu’on se place dans un système de coordonnées cylindriques associé à la conduite (faire un dessin si ça peut vous aider).
$\bullet$ expliciter l’élément infinitésimal de surface $dS = rdrd\theta$
$\bullet$ écrire les bornes des deux intégrales (sur $r$ et $\theta$ ).

L’intégrale prend alors la forme suivante :

$D_m = \int_{r=0}^{a} \int_{\theta=0}^{2\pi} \rho v(r) rdrd\theta .$

Cette intégrale se calcule facilement, et donne après simplification :

$D_m = \frac{\rho \pi a^4}{8 \eta L} \Delta P .$

3) L’énoncé donne implicitement le débit massique (masse par unité de temps) $D_m = masse/temps = 0.011$ kg.s $^{-1}$ . On isole $\eta$ dans l’équation précédente : $\eta = \frac{\rho \pi a^4}{8 L D_m} \Delta P$

L’application numérique (pour gagner du temps, ne faire qu’un ordre de grandeur) donne : $\eta = 9.3\times 10^{-3}$ Pl. (comme dans tout calcul, attention aux unités)

Cette valeur est un peu élevée mais cohérente avec la viscosité de l’eau tabulée : $\eta = 10^{-3}$ Pl. On peut argumenter en disant que lorsque $H$ diminue, $\Delta P$ diminue également, donc le débit baisse un peu, ce qui donne l’illusion que le fluide est plus visqueux.

4) Pour déterminer le type d’écoulement, il faut calculer le nombre de Reynolds défini dans le cours par $Re = \rho \cdot \text{vitesse}\cdot \text{taille caract.} / \eta$ . Ici, on peut prendre la vitesse au centre du tube, et la taille caractéristique est le rayon de la conduite $a$ . On obtient alors $Re \sim 100$ . On est donc en régime laminaire ( $Re<2000$ ).

Lire d’autres contenus pour progresser :

N'hésite pas à partager l'article

Colle de physique en prépa tombée aux concours

Exemple de colle de physique en prépa scientifique pour s’entraîner

STAGE INTENSIF EN PRÉPA SCIENTIFIQUE

Profite de tes vacances pour progresser en vue des concours.

Exercice 1 : khôlle de physique optique, un grand classique

STAGE INTENSIF EN PRÉPA SCIENTIFIQUE

Profite de tes vacances pour progresser en vue des concours.

Exercice 2 (d’après Centrale PSI 2016) : colle de physique en mécanique des fluides

COURS PARTICULIERS DE PHYSIQUE

Nous avons recruté pour vous les meilleurs profs de physique.

POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Exemple de colle de physique en prépa scientifique pour s’entraîner

STAGE INTENSIF EN PRÉPA SCIENTIFIQUE

Profite de tes vacances pour progresser en vue des concours.

Exercice 1 : khôlle de physique optique, un grand classique

STAGE INTENSIF EN PRÉPA SCIENTIFIQUE

Profite de tes vacances pour progresser en vue des concours.

Exercice 2 (d’après Centrale PSI 2016) : colle de physique en mécanique des fluides

COURS PARTICULIERS DE PHYSIQUE

Nous avons recruté pour vous les meilleurs profs de physique.

POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES

Comment bien lire Le Banquet ? – français/philo en prépa scientifique

Le Choc des Titans : l’X ou l’ENS ?

La démocratie aux Etats-Unis pour prepa scientifique

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales