Chapitres de maths en 1ère

Exercices sur la dérivation en première

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Première

Ces exercices sur la dérivation en 1ère permettent aux élèves de s’entraîner sur ce chapitre en mettant le cours en ligne de maths en première sur la derivation en application. Des exercices sur d’autres chapitres sont aussi disponibles sur notre site : des exercices sur les suites numériques, des exercices sur les séries arithmétiques et géométriques, des exercices sur le second degré, etc. N’hésitez pas à faire appel à nos cours de maths si vous souhaitez progresser sur les fonctions et dérivations.

Exercice dérivation première 1

Soit $f$ la fonction définie sur $\mathbb{R}$ par: $f(x)=-3x^4+2x-1.$ On note $\mathscr{C}_f$ la courbe représentative de $f$ dans un repère orthonormé.

Question 1 :

Écrire l’équation de la droite tangente à $\mathscr{C}_f$ au point $A(-1;-6)$ .

Question 2 :

Les droites tangentes à $\mathscr{C}_f$ en $-1$ et en $1$ sont-elles parallèles ?

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 1 sur la dérivation

Question 1 :

Soit $f$ la fonction définie sur $\mathbb{R}$ par: $f(x)= -3x^{4}+2x-1$ .

On note $\mathscr{C}_{f}$ la courbe représentative de $f$ dans un repère orthonormé.

Équation de la droite tangente à $\mathscr{C}_{f}$ au point $A(-1;-6)$ :

L’équation réduite de la droite tangente en ce point est donnée par :

$y=f(-1)+f'(-1)(x+1)$

Comme $f(-1)=-6$ et pour tout $x\in \mathbb{R}$ , $f'(x)=-12x^3+2$ donc $f'(-1)=14$ , alors $y=-6+14\times(x+1)$ .

D’où, l’équation de la tangente à $\mathscr{C}_{f}$ au point $A(-1;-6)$ est $y=14x+8$ .

Question 2 :

Les droites tangentes à $\mathscr{C}_{f}$ aux points d’abscisses $-1$ et $1$ sont parallèles si et seulement si leurs coefficients directeurs égaux.

Or, $f'(1)= -10\neq f'(-1)=14$ alors les droites tangentes à $\mathscr{C}_{f}$ aux points d’abscisses $-1$ et $1$ ne sont pas parallèles.

Fonction dérivée exercice corrigé 2

On considère la fonction définie sur $\mathbb{R}$ par $f x\mapsto x^3+x-10$ .

Question 1 :

Montrer que la fonction $f$ est strictement croissante sur $\mathbb{R}$ .

Question 2 :

Vérifier que $f(2) = 0$ . En déduire le signe de $f(x)$ sur $\mathbb{R}$

Question 3 :

Montrer que, pour tout $x\in[2;+\infty[,$ $x^3\geq 10-x$ .

Correction de l’exercice 2 sur la fonction dérivée

Question 1 exercice dérivée premiere :

On considère la fonction définie sur $\mathbb{R}$ par $f: x \longmapsto x^3 +x -10$ .

La fonction $f$ est une fonction polynôme donc elle est définie et dérivable sur $\mathbb{R}$ .

Pour tout $x\in \mathbb{R}$ , $f'(x)=3x^2+1>0$ donc la fonction $f$ est strictement croissante sur $\mathbb{R}$ .

Question 2 fonction dérivée exercice corrigé :

$f(2)=2^3+2-10=0$ donc $2$ est une solution de l’équation $f(x)=0$ .

Par la propriété de factorisation d’un polynôme, l’expression de $f(x)$ peut s’écrire (un réel $\alpha$ est une racine d’un polynôme si et seulement si on peut factoriser ce polynôme par $(x-\alpha)$

$f(x)=(x-2)(ax^2+bx+c)$

$=ax^2+(b-2a)x^2+(c-2b)x-2c$

Par identification les coefficients de même degré sont égaux, on obtient le système d’équations:

$\begin{cases} a=1 \\ b-2a=0 \\ c-2b=1 \\ -2c=10 \end{cases}$

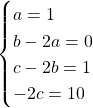
Ce qui donnent $a=1$ , $b=2$ et $c=5$

L’équation du second degré $x^2+2x+5=0$ a pour discriminant $\Delta=4-4\times5=-16<0$ .

Donc, pour tout $x\in \mathbb{R}$ , $x^2+x+5>0$ . C’est-à- dire que $f(x)$ est du signe de $x-2$ .

Question 3 fonction dérivée exercice corrigé première :

On sait que $f(2)=0$ et la fonction $f$ est strictement croissante sur $\mathbb{R}$ ,

En particulier sur $[2;+\infty[$ alors pour tout réel $x\geq 2$ , $f(x)-f(2) \geq 0$ .

Par conséquent :

$\forall x\in [2;+\infty[, x^{3}\geq 10-x.$

Variation de fonctions : exercice derivation premiere 3

Soit $g$ la fonction rationnelle définie sur $\mathscr{D}_g=\mathbb{R}\setminus \{-2\}$ par : $g(x)=\dfrac{4x^2+7x-1}{x+2}.$

On note $\mathscr{C}_g$ la courbe représentative de $g$ dans un repère orthonormé.

Question 1 exercice dérivation première :

Trouver les réels $a,b$ et $c$ pour que: $g(x)=ax+b+\dfrac{c}{x+2}$

Question 2 derivation exercice corrigé :

Justifier la dérivabilité de $g$ sur $\mathscr{D}_g$ .

Question 3 exercice derivation :

Montrer que pour tout $x\in\mathscr{D}_g$ : $g'(x)=4-\dfrac{1}{(x+2)^2}$

Question 4 dérivée première exercice :

En déduire une factorisation de $g'(x)$ . Dresser le tableau de varition de $g$ .

Question 5 exercice dérivée corrigé :

Etudier les positions relatives de $\mathscr{C}_g$ par rapport à la droite d’équation $y=4x-1.$

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 3 sur les variations de fonctions

Question 1 exercice corrige derivation premiere :

Soit $g$ la fonction rationnelle définie sur $\mathscr{D}_g=\mathbb{R}\setminus\{2\}$ par :

$g(x)=\dfrac{4x^{2}+7x-1}{x+2}$

On note $\mathscr{C}_g$ la courbe représentative de $g$ dans un repère orthonormé.

Calcule de $a,b,c$ .

$g(x)=\dfrac{4x^{2}+7x-1}{x+2}$

$=\dfrac{4x^2+8x-x-2+1}{x+2}$

$=\dfrac{4x(x+2)-(x+2)+1}{x+2}$

$=\dfrac{(x+2)(4x-1)+1}{x+2}$

$=4x-1+\dfrac{1}{x+2}$

Par identification on a $a=4, b=-1$ et $c=1$ .

Question 2 :

La fonction $x\mapsto \dfrac{1}{x+2}$ est une fonction rationnelle définie et dérivable sur $\mathbb{R}\setminus\{2\}$ .

La fonction $x\mapsto 4x-1$ est une fonction polynôme

Donc définie et dérivable sur $\mathbb{R}$ donc aussi sur $\mathbb{R}\setminus\{2\}$ .

Ainsi, $g$ est la somme de deux fonctions définies et dérivables sur $\mathbb{R}\setminus\{2\}$

Donc elle est aussi définie et dérivable sur $\mathbb{R}\setminus\{2\}$ .

Question 3 exercice dérivée corrigé :

Pour tout $x \in \mathscr{D}_g$ :

$g'(x)=4-\dfrac{1}{(x+2)^2}.$

Question 4 :

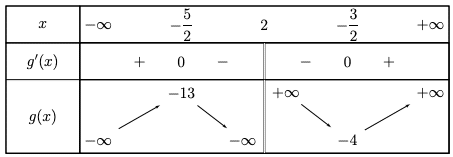
Tableau de variation de $g$ .

$g'(x)=4-\dfrac{1}{(x+2)^2}$

$=2^2-\left(\dfrac{1}{x+2}\right)^2$

$=\left(2+\dfrac{1}{x+2}\right)\left(2-\frac{1}{x+2}\right)$

$=\left(\dfrac{2x+5}{x+2}\right)\left(\frac{2x+3}{x+2}\right)$

donc $g'(x)=\dfrac{1}{(x+2)^2}(2x+5)(2x+3)$

Pour tout $x\in\mathscr{D}_g$ , $(x+2)^2>0$ . Donc, $g'(x)$ est du signe de $(2x+5)(2x+3)$ . D’où le tableau de signe de $g'(x)$ :

Ce qui permet d’obtenir le tableau de variation de $g$ :

Question 5 exercice corrigé derivation :

Les positions relatives de $\mathscr{C}_g$ par rapport à la droite d’équation $y=4x-1$ .

Appelons $\mathscr{T}$ cette droite. On a:

$g(x)-y=4x-1+\dfrac{1}{x+2}-4x+1=\dfrac{1}{x+2}$

Ainsi :

$\bullet$ Pour $x<-2$ , $g(x)-y<0$ , donc la courbe $\mathscr{C}_g$ est en dessous de $\mathscr{T}$ .

$\bullet$ Pour $x>-2$ , $g(x)-y>0$ , donc la courbe $\mathscr{C}_g$ est au-dessus de $\mathscr{T}$ .

Les élèves trouveront d’autres exercices sur la dérivation en 1ère beaucoup plus complets sur l’application mobile PrepApp et des exercices sur d’autres chapitres : exercices sur la fonction exponentielle, etc.

Exercices sur la dérivation en première

Exercice dérivation première 1

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Correction de l’exercice 1 sur la dérivation

Fonction dérivée exercice corrigé 2

Correction de l’exercice 2 sur la fonction dérivée

Variation de fonctions : exercice derivation premiere 3

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Correction de l’exercice 3 sur les variations de fonctions

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales