Chapitres de maths en Terminale D

Exercices et corrigés sur les équations différentielles en Terminale D

Vous trouverez ci-dessous des exercices corrigés gratuits sur les équations différentielles pour les élèves préparant le bac D.

Application directe du cours sur les équations différentielles

Question 1 :

La solution $f$ de l’équation différentielle $y'+2\, y = 6$ qui vérifie la condition initiale $f (0) = 1$ est définie sur l’ensemble $\mathbb{R}$ des nombres réels par :

a. $f (x) = -2\, \textrm{e} ^{ -2\, x} +3$

b. $f (x) = -2\, \textrm{e} ^{2\, x} +3$

c. $f (x) = -2\, \textrm{e} ^{ -2x} -3$

Question 2 :

Soit $f$ la fonction solution sur $\mathbb{R}$ de l’équation différentielle $y' = -y +2$ telle que $f (\ln2) = 1$ .

La courbe représentative de $f$ admet au point d’abscisse 0, une tangente d’équation $y = 2\,x$

Question 3 :

$y' = 3\, y$ et $y(0) = 1$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Corrigé des applications sur les équations différentielles

Question 1 :

En utilisant le résultats de cours avec $a = - 2$ et $b = 6$ , la solution générale est $x \mapsto k \,\textrm{e} ^{a\, x} - \dfrac {b} a$ où $k\in \mathbb{R}$

soit $f : x \mapsto k \,\textrm{e} ^{ - 2\, x} + \dfrac 6 2$ .

$f(0) = 1$ ssi $k + 3 = 1$ ssi $k = - 2$ .

La fonction solution est

$\boxed{\mathbb{R} \to \mathbb{R}, \, x \mapsto - 2\,\textrm{e} ^{ - 2\, x } + 3}$ .

Question 2 :

La solution générale de $y' = -y +2$ est $x \mapsto k\, \textrm{e} ^{- x} + 2$ où $k \in \mathbb{R}$ .

$y(\ln(2)) = 1$ ssi $k \,\textrm{e} ^{ - \ln(2)} + 2 = 1$

ssi $\displaystyle \dfrac k 2 = - 1$ ssi $k = - 2$

Alors $f : x \mapsto - 2\, \textrm{e} ^{ - x} + 2$ .

$f(0) = 0$ et $f'(0) = - f(0) + 2 = 2$ .

La tangente en $(0 , 2)$ a pour équation

$y = f'(0)(x - 0) + f(0)$ soit $\boxed{y = 2 \, x }$ .

Question 3 :

L’ensemble des solutions est l’ensemble des fonctions $x \mapsto k \, \textrm{e} ^{ 3\, x}$ où $k \in \mathbb{R}$ .

$f : x \mapsto k \, \textrm{e} ^{ 3\, x}$ vérifie $f(0) = 1$ ssi $k = 1$ .

La solution est $\boxed{f : x \mapsto \textrm{e} ^{ 3\, x} }$ .

Exercices terminale D : équations différentielles plus compliquées

Exercice 1

Question 1

Déterminer les solutions de $\quad y'' - 6 \, y' + 3\, y = \dfrac {1 - x} { x ^3} \textrm{e}^{ 3\,x}$

sur $I =\; ]0 , + \infty[$ .

Exercice 1 (fin)

Question 2

Démontrer et déterminer qu’il existe une seule solution $f$ telle que $f(1) = 0$ et $f'(1) = 0$ .

Corrigé des exercices sur les équations différentielles

Corrigé de l’exercice sur la question 1

Comme la fonction $x \mapsto \textrm{e}^{ 3\,x}$ ne s’annule pas, la fonction $f$ est deux fois dérivable ssi la fonction $u$ définie par

$\qquad \qquad u : x \mapsto \textrm{e}^{ - 3\,x} \, f(x)$ est deux fois dérivable sur $I$ .

En notant donc pour $x \in I$ , $f(x) = u(x)\, \textrm{e}^{ 3\,x}$

$f'(x) = u'(x) \, \textrm{e}^{ 3\,x} + 3 \, u(x) \, \textrm{e}^{ 3\,x}$

$f'(x) = (u'(x) + 3\, u(x)) \, \textrm{e}^{ 3\,x}$

et $f''(x) = (u''(x) + 3\, u'(x)) \, \textrm{e}^{ 3\,x}$ $\qquad \qquad\quad + \, 3\, (u'(x) + 3\, u(x)) \, \textrm{e}^{ 3\,x}$

$f''(x) = (u''(x) + 6\, u'(x) + 9\, u(x) ) \, \textrm{e}^{ 3\,x}$

$f$ est solution sur $I$ ssi pour tout $x \in I$ ,

$\left ( \, u''(x) + (6 - 6) \, u'(x)\right.$

$\qquad \qquad \left. + \, (9 -18 + 9) \, u(x) \, \right ) \, \textrm{e}^{ 3\,x}$ $\qquad \qquad \qquad = \dfrac {1 - x} { x ^3} \textrm{e}^{ 3\,x}$

ssi pour tout $x \in I$ , $\qquad u''(x) = \dfrac {1 - x} { x ^3} = \dfrac 1 {x ^3} - \dfrac 1 {x ^2}$

ssi il existe $a \in \mathbb{R}$ tel que pour tout $x \in I$ , $\qquad \quad u'(x) = \dfrac { - 1} {2\, x ^2} + \dfrac 1 {x} + a$

ssi il existe deux réels $a$ et $b$ tels que pour tout $x \in I$ , $\qquad \quad u(x) = \dfrac 1 {2\, x} + \ln(x) + a \, x + b$ .

L’ensemble des solutions est l’ensemble des fonctions

$\quad x \mapsto \left ( \dfrac 1 {2\, x} + \ln(x) + a \, x + b \right ) \, \textrm{e}^{ 3\,x}$

où $a$ et $b$ sont réels.

Corrigé de l’exercice sur la question 2 en terminale D

On cherche $a$ et $b$ tels que $f(1) = 0$ et $f'(1) = 0$ .

En utilisant $f(x) = u(x) \, \textrm{e} ^{3\, x}$

et $f'(x) = (3\, u(x) + u'(x)) \, \textrm{e} ^{3\, x}$

on obtient les conditions équivalentes

$u(1) = 0$ et $3\, u(1) + u'(1) = 0$

ssi $u(1) = u'(1) = 0$

ssi $\dfrac 1 2 + a + b = 0$ et $\dfrac {-1} 2 + \dfrac 1 1 + a = 0$

ssi $a = - \dfrac 1 2$ et $b = - \dfrac 1 2 - a = 0$

Le problème admet une unique solution définie par

$\boxed{f : x \mapsto \left ( \dfrac 1 {2\, x} + \ln(x) - \dfrac 1 2 x \right ) \, \textrm{e}^{ 3\,x}}$ .

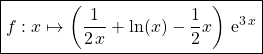Retrouvez d’autres exercices et corrigés des cours de maths niveau terminale D :