Mon parcours pour réussir en maths
J'aprends le cours par coeur
Je travaille avec un prof de maths
Je travaille entre chaque séance
Avis Google France
★★★★★ 4,8 sur 5
Exercices corrigés sur les équations de droites en seconde
Résumé de cours Exercices et corrigés
Cours en ligne de Seconde Générale
Nos exercices sur les équations de droites offrent aux élèves de seconde une manière ludique et éducative de se familiariser avec les concepts de vecteurs et d’équations cartésiennes. Un incontournable pour ceux qui souhaitent exceller en maths. Pour une progression encore plus solide, envisager de faire appel à un prof de maths à domicile. Un tel accompagnement offre une approche adaptée en 2nde, permet de cibler et de surmonter les difficultés et encourage une meilleure compréhension des concepts, essentielle pour une maîtrise complète des mathématiques.
Exercice 1 de mathématique sur les équations de droites niveau seconde
On considère une droite ![]() et quatre points
et quatre points ![]() ,
, ![]() ,
, ![]() et
et ![]() représentés sur la figure ci-après.
représentés sur la figure ci-après.

À partir des informations sur le graphique :
1. Montrer que le vecteur ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() .
.
2. Déterminer le réel ![]() tel que
tel que ![]() .
.
3. En déduire que le vecteur ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() .
.
Avis Google France ★★★★★ 4,9 sur 5COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité En ligne ou à domicile
Exercice 2 de maths d’équation de droite en 2nde
1. Déterminer une équation cartésienne à coefficients entiers de la droite d’équation réduite :
(a) ![]()
(b) ![]()
2. Donner l’équation réduite de la droite ayant pour équation cartésienne:
(a) ![]()
(b) ![]()
Quiz 3 de maths pour réviser les équations de droites en seconde
Soit ![]() une droite d’équation cartésienne
une droite d’équation cartésienne ![]() .
.
Dire si l’affirmation est vraie ou fausse. Démontrer votre réponse.
1. Tout vecteur directeur de ![]() est colinéaire au vecteur
est colinéaire au vecteur ![]() .
.
2. La droite ![]() peut ne pas avoir une équation réduite.
peut ne pas avoir une équation réduite.
3. Pour tous réels ![]() et
et ![]() , il existe un réel
, il existe un réel ![]() tel que
tel que ![]() est un vecteur directeur de
est un vecteur directeur de ![]() .
.
4. Il existe une droite ![]() , sécante
, sécante ![]() telle que
telle que ![]() .
.
5. Pour ![]() , il existe des réels a, b, c tel que le coefficient directeur de
, il existe des réels a, b, c tel que le coefficient directeur de ![]() est égale à son ordonnée à l’origine.
est égale à son ordonnée à l’origine.
6. Pour tout couple de réel ![]() ,
, ![]() dès que
dès que ![]() et
et ![]() sont non nuls.
sont non nuls.
Exercice 4 sur les équations de droite en maths pour la seconde
On donne deux droites d’équation ![]() et
et ![]() .
.
Démontrer que la fonction IntersectionDroite codée en Python suivante permet de déterminer si les droites ![]() et
et ![]() sont parallèles et renvoie aux coordonnées du point d’intersection de
sont parallèles et renvoie aux coordonnées du point d’intersection de ![]() et de
et de ![]() si les deux droites sont sécantes.
si les deux droites sont sécantes.

STAGE INTENSIF EN 2NDE
Réussir la 2nde avec les stages de vacances en maths, physique-chimie et français
–> Les enseignants bienveillants et pédagogues
–> Des progrès assurés avec les stages de vacances
–> Format classe inversée et différenciation
Avis Google France ★★★★★ 4,9 sur 5
Corrigé de l’exercice 1 de maths en seconde sur les equations de droites
On a la droite ![]() et quatre points
et quatre points ![]() ,
, ![]() ,
, ![]() et
et ![]() du plan.
du plan.
1. Par lecture graphique:
Les coordonnées du point ![]() sont
sont ![]() et celles de
et celles de ![]()
![]() ;
;
La droite ![]() passe par les points de coordonnées
passe par les points de coordonnées ![]() et
et ![]() que l’on notera respectivement par
que l’on notera respectivement par ![]() et
et ![]() .
.
À partir des coordonnées des points ![]() ,
, ![]() ,
, ![]() et
et ![]() , on a :
, on a :
Les coordonnées du vecteur ![]() sont
sont ![]() .
.
Les coordonnées du vecteur ![]() sont
sont ![]() .
.
Alors, ![]() .
.
Ce qui implique que les vecteurs ![]() et
et![]() sont colinéaires.
sont colinéaires.
Comme le vecteur ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() et un vecteur colinéaire à un vecteur directeur est un vecteur directeur, alors le vecteur
et un vecteur colinéaire à un vecteur directeur est un vecteur directeur, alors le vecteur ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() .
.
2. Par lecture graphique, on a les coordonnées :
Du point ![]() ;
;
Du point ![]() .
.
Donc, ![]() a pour coordonnées
a pour coordonnées ![]() .
.
Or, ![]() a pour coordonnées
a pour coordonnées ![]() . Alors, pour que
. Alors, pour que ![]() ,
, ![]() .
.
3. D’après la question 2., il existe ![]() tel que
tel que
![]() .
.
Donc, les vecteurs ![]() et
et ![]() sont colinéaires.
sont colinéaires.
On en déduit que le vecteur ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() .
.
Réponse à l’exercice 2 de maths sur les équations de droites en seconde
1. a) En multipliant l’équation ![]() par 3, on a les équivalences:
par 3, on a les équivalences:
![]()
![]()
Donc, à partir de l’équation réduite ![]() , on obtient l’équation cartésienne
, on obtient l’équation cartésienne ![]() .
.
b) En multipliant l’équation ![]() par 4, on a les équivalences:
par 4, on a les équivalences:
![]()
![]()
Donc, à partir de l’équation réduite ![]() , on obtient l’équation cartésienne
, on obtient l’équation cartésienne ![]() .
.
2. a) En isolant ![]() dans l’équation
dans l’équation ![]() , on a les équivalences:
, on a les équivalences:
![]()
![]()
Alors, à partir de l’équation cartésienne ![]() , on obtient l’équation réduite
, on obtient l’équation réduite ![]() .
.
b) En isolant ![]() dans l’équation
dans l’équation ![]() , on a les équivalences :
, on a les équivalences :
![]()
![]()
Alors, à partir de l’équation cartésienne ![]() , on obtient l’équation réduite
, on obtient l’équation réduite ![]() .
.
Correction au QCM 3 sur les équations de droite en maths niveau seconde
On considère une droite ![]() d’équation cartésienne
d’équation cartésienne ![]() .
.
1. Vrai. Par raisonnement direct.
D’après l’équation cartésienne de la droite ![]() , le vecteur
, le vecteur ![]() est un vecteur directeur. Comme
est un vecteur directeur. Comme ![]() , alors le vecteur
, alors le vecteur ![]() est un vecteur directeur de
est un vecteur directeur de ![]() . Comme tout vecteur colinéaire à un vecteur directeur est un vecteur directeur, alors tout vecteur directeur de
. Comme tout vecteur colinéaire à un vecteur directeur est un vecteur directeur, alors tout vecteur directeur de ![]() est colinéaire au vecteur
est colinéaire au vecteur ![]() .
.
2. Vrai.
L’équation réduite d’une droite est de la forme ![]() où
où ![]() et
et ![]() sont des réels. Dans le cas où
sont des réels. Dans le cas où ![]() , l’équation
, l’équation ![]() est réduite à
est réduite à ![]() . Donc, il est impossible d’exprimer
. Donc, il est impossible d’exprimer ![]() en fonction de
en fonction de ![]() . En résumé, les droites verticales n’ont pas d’équation réduite. Le coefficient directeur d’une droite verticale n’est pas défini.
. En résumé, les droites verticales n’ont pas d’équation réduite. Le coefficient directeur d’une droite verticale n’est pas défini.
3. Faux. Par l’absurde
On suppose que pour tout ![]() , il existe un réel
, il existe un réel ![]() tel que
tel que ![]() soit un vecteur directeur de
soit un vecteur directeur de ![]() . Comme les vecteurs directeurs sont colinéaires alors le déterminant
. Comme les vecteurs directeurs sont colinéaires alors le déterminant ![]() . Ce qui donne l’équation
. Ce qui donne l’équation ![]() . Cette équation mène à une contradiction en choisissant
. Cette équation mène à une contradiction en choisissant ![]() et
et ![]() . Ainsi, il existe au moins un couple
. Ainsi, il existe au moins un couple ![]() où cette assertion est fausse.
où cette assertion est fausse.
4. Faux. Raisonnement par l’absurde.
On suppose qu’il existe une droite ![]() d’équation cartésienne
d’équation cartésienne ![]() sécante à
sécante à ![]() mais
mais ![]() .
.
- Les droites
 et
et  sont sécantes, alors leurs vecteurs directeurs ne sont pas colinéaires. C’est-à-dire que le déterminant
sont sécantes, alors leurs vecteurs directeurs ne sont pas colinéaires. C’est-à-dire que le déterminant
![]()
- L’intersection
 est vide, alors le système
est vide, alors le système  n’a pas de solution. Ce qui donne
n’a pas de solution. Ce qui donne  .
.
Ces deux affirmations sont contradictoires. Donc, l’affirmation ne peut pas être vraie.
5. Vrai. Par raisonnement direct.
Si ![]() a une équation cartésienne
a une équation cartésienne ![]() avec
avec ![]() alors
alors ![]() a pour équation réduite
a pour équation réduite ![]() . Donc, son coefficient directeur vaut
. Donc, son coefficient directeur vaut ![]() et son ordonnée à l’origine vaut
et son ordonnée à l’origine vaut ![]() . Par conséquent, pour un réel non nul
. Par conséquent, pour un réel non nul ![]() , il suffit que
, il suffit que ![]() pour avoir l’égalité entre le coefficient directeur et l’ordonnée à l’origine.
pour avoir l’égalité entre le coefficient directeur et l’ordonnée à l’origine.
6. Faux. Un contre exemple.
En prenant ![]() et
et ![]() . Alors, on obtient
. Alors, on obtient ![]() . Donc, on a un couple de réel
. Donc, on a un couple de réel ![]() tel que
tel que ![]() et
et ![]() ne sont pas nuls alors que
ne sont pas nuls alors que ![]()
Avis Google France ★★★★★ 4,9 sur 5COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Corrigé du test 4 de maths sur les équations de droite en seconde
On a deux droites d’équation ![]() et
et ![]() .
.
Par raisonnement direct.
On considère la fonction {\color{manga} IntersectionDroite} codée en Python.
Les lignes 2,…,7 correspondent aux saisis des coefficients ![]() et
et ![]() de deux droites.
de deux droites.
La ligne 8 est une expression conditionnelle qui teste si ![]() . C’est-à-dire,
. C’est-à-dire, ![]() .
.
Or ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() et
et ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() .
.
Alors, si ![]() , c’est à dire si
, c’est à dire si ![]() , les vecteurs
, les vecteurs
![]()
et ![]() sont deux vecteurs colinéaires. Donc, les droites
sont deux vecteurs colinéaires. Donc, les droites ![]() et
et ![]() sont parallèles.
sont parallèles.
La ligne 9 correspond au cas où le test est vrai et affiche le résultat.
Les lignes 10 et 11 correspondent au cas contraire. C’est-à-dire que les droites ![]() et
et ![]() sont sécantes. Donc, le système
sont sécantes. Donc, le système 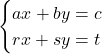 admet une solution.
admet une solution.
Par la méthode par addition.
- Éliminer
 pour calculer
pour calculer  .
.
En multipliant la première équation par ![]() et la deuxième équation par
et la deuxième équation par ![]() , on obtient:
, on obtient:
![Rendered by QuickLaTeX.com \[ \begin{cases} -rax-rby=-rc\\ arx+asy=at \end{cases} \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-13c26113adbcf7febf0d95798bc0a65a_l3.png)
Par addition, on a ![]() . Ce qui donne
. Ce qui donne ![]() . Donc,
. Donc, ![]() .
.
Ce qui correspond à la deuxième valeur de retour à la ligne 11.
- Éliminer
 pour calculer
pour calculer  .
.
En multipliant la première équation par ![]() et la deuxième équation par
et la deuxième équation par ![]() , on obtient:
, on obtient:
![Rendered by QuickLaTeX.com \[ \begin{cases} sax+sby=sc\\ -brx-bsy=-bt \end{cases} \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-03655a0257361a52940659ad99f8e4d1_l3.png)
Pa addition, on a ![]() . Ce qui donne
. Ce qui donne ![]() . Donc,
. Donc, ![]() . C’est-à-dire,
. C’est-à-dire, ![]() .
.
Ce qui correspond à la première valeur de retour à la ligne 11.
Par conséquent, l’algorithme affiche que les deux droites sont parallèles à la ligne 9 si le test est vrai, et retourne les coordonnées du point d’intersection à la ligne 11 sinon.
Consultez nos exercices en ligne de maths en seconde générale :
- Exercices avec correction sur les pourcentages en seconde
- Test avec corrigé gratuits de maths sur les statistiques en seconde
- Entrainement de maths niveau seconde sur les probabilités
- Ensembles et arithmétique : Exercices d’entrainements niveau seconde
- Quiz de maths pour la seconde sur les ensembles et intervalles
- Résumé de cours gratuit : Les pourcentages niveau seconde
- Maths : Comprendre facilement les statistiques en seconde


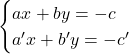 n’a pas de solution. Ce qui donne
n’a pas de solution. Ce qui donne