Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Avis Google France
★★★★★ 4,8 sur 5

Exercices et corrigés sur les fonctions de référence en seconde

Résumé de cours Exercices et corrigés

Cours en ligne de Seconde Générale

Travailler sur des exercices de fonctions de référence en seconde vous prépare à réussir en maths pour votre année de seconde mais vous prépare également à la spécialité maths en 1ère. Ils sont conçus pour solidifier vos bases et vous donner confiance dans vos compétences. Si vous ressentez le besoin d’un soutien supplémentaire, un prof de maths peut être la solution. Il vous offrira une attention individuelle, des explications et des stratégies adaptées à votre manière d’apprendre. Ce ‘petit plus’ peut faire une grande différence, transformant les défis en opportunités d’apprentissage et renforçant votre compréhension globale des mathématiques.

Exercice 1 de maths pour réviser les fonctions de référence en 2nde

Donner le plus petit intervalle contenant $x$ dans chacun des cas suivants :

1. $55>\sqrt{x}>32$ .

2. $0<\dfrac{1}{x^2}\leq1$ .

3. $15\geq |x| >4$ .

Entrainement de seconde en maths pour réviser les fonctions de référence

Le tableau suivant donne les variations d’une fonction du second degré $f$ . On note $\mathscr{C}_f$ la parabole qui représente $f$ dans un repère orthonormé.

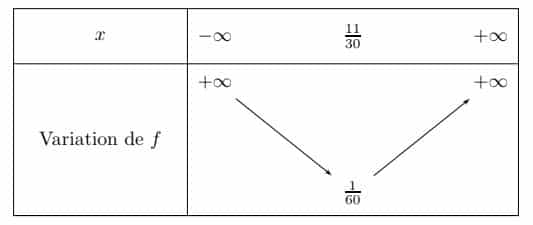
1. Comparer $f(-1)$ et $f(-2)$ .

2. Montrer que pour tout $x\in \mathbb{R}$ , $f(x)>0$ .

3. Donner les coordonnées du sommet $S$ de la parabole $\mathscr{C}_f$ .

4. On suppose que $f(0)=2$ . Déterminer la forme canonique de $f$ .

5. En déduire l’expression de $f$ sous forme développée.

Test 3 de maths niveau seconde sur les fonctions de référence

À l’aide des variations d’une fonction ou de plusieurs fonctions de référence :

1. Comparer $\sqrt{12^3}$ et $\sqrt{13^3}$ puis $\left((-2)^3\right)^2$ et $\left(\dfrac{3^2}{2^2}\right)^3$

2. Comparer $\sqrt{\dfrac{1}{7}}$ et $\dfrac{1}{3}$ , $\dfrac{1}{\sqrt{16^3}}$ et $\dfrac{1}{65}$ .

Donner toutes les étapes des effets des variations des fonctions sur les inégalités.

Question 4 en maths pour s’entrainer aux fonctions de référence en seconde

Pour un réel $x$ , déterminer le plus petit intervalle qui contient $\dfrac{1}{x}$ , $\dfrac{1}{x^2}$ et $-\dfrac{1}{|x|}$ pour $-\dfrac{7}{4}>x>-\dfrac{13}{3}$ .

PARTICIPER À UN STAGE INTENSIF EN 2nde

C’est gagner des points sur ta moyenne !

Corrigé de l’exercice 1 sur les fonctions de référence en maths seconde

On considère un réel $x$ .

1. Par la croissance de la fonction carré sur $[0;+\infty[$ , $55>\sqrt{x}>32 \Longrightarrow 55^2>\sqrt{x}^2> 32^2$ .

Ce qui donne $3025>x>1024$ .

Donc, pour $55>\sqrt{x}>32,\ x \in \left] 1024;3025 \right[$ .

2. Par la décroissance de la fonction inverse sur $]0;+\infty[$ ,

$0<\dfrac{1}{x^2}\leq1$ implique $1\leq x^2$

Puis par la croissance de la fonction racine carrée sur $]0;+\infty[$ ,

On obtient $1\leq \sqrt{x^2}$ .

Comme $\sqrt{x^2}=|x|$ et que pour tout $x>0$ , $|x|=x$

Alors $1\leq x$ .

Donc, $x\in [1;+\infty[$ .

3. Par disjonction des cas,

Si $x\geq 0$ , alors $|x|=x$ . Donc, $15\geq x >4$ ;

Si $x<0$ , alors $|x|=-x$ .

Donc, $15\geq -x >4$ .

En multipliant par $-1$ , on obtient $-15 \leq x <-4$ .

Ainsi, pour $15\geq |x| >4,\ x \in [-15;-4 [\cup ]4;15]$ .

Correction du quiz 2 de mathématique pour comprendre les fonctions de référence en seconde générale

On a une fonction de seconde degré $f$ représentée par la parabole $\mathscr{C}_f$ dans un repère orthonormé.

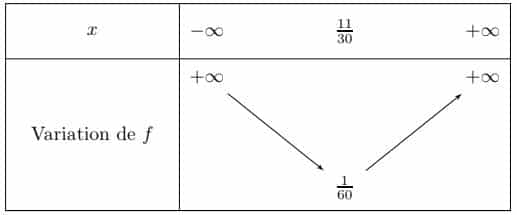
1. Par lecture du tableau de variation de $f,\ f$ est strictement décroissante sur $\left]-\infty;\tfrac{11}{30} \right[$ .

Comme $-1, -2 \in \left]-\infty;\tfrac{11}{30} \right[$

Alors $-1>-2$ entraîne $f(-1)<f(-2)$ .

2. Raisonnement direct.

Par lecture du tableau de variation de $f$ :

$f$ est strictement décroissante sur $\left]-\infty;\tfrac{11}{30} \right[$ ;

$f$ est strictement croissante sur $\left]\tfrac{11}{30}; +\infty\right[$ ;

Donc, $f$ admet un minimum en $\dfrac{11}{30}$ .

C’est-à-dire, pour tout $x\in \mathbb{R}$ ,

$f(x)\geq f(\dfrac{11}{30})$ .

Or, $f(\dfrac{11}{30})=\dfrac{1}{60}>0$ .

Par conséquent, pour tout $x\in \mathbb{R}$ , $f(x)>0$ .

3. D’après la question précédente, $f$ atteint son minimum en $\dfrac{11}{30}$ et sa valeur minimale est $f(\frac{11}{30})=\dfrac{1}{60}$ .

Donc, le sommet de la parabole est

$S\left(\dfrac{11}{30};\dfrac{1}{60}\right)$ .

Sachant que :

Sous forme canonique,

$f(x)=a(x-\alpha)^2+\beta$ avec $a$ un réel à déterminer

Et $(\alpha;\beta)$ les coordonnées du sommet $S$ de la parabole $\mathscr{C}_f$ .

Comme $f(0)=2$ ,alors, $a\left(0-\dfrac{11}{30}\right)^2-\dfrac{1}{60}=2$ .

Ce qui donne $a=\left(2+\dfrac{1}{60}\right)\times \dfrac{30^2}{11^2}=15$ .

D’où, la forme canonique de $f$ : $f(x)=15\left(x-\dfrac{11}{30}\right)^2-\dfrac{1}{60}$ .

5. En développant la forme canonique de $f$ dans la question 4., on a:

$f(x)= 15\left(x-\dfrac{11}{30}\right)^2-\dfrac{1}{60}$

$f(x)= 15\left(x^2-2 \times x\times \dfrac{11}{30} + \dfrac{11^2}{30^2} \right)-\dfrac{1}{60}$

$f(x)= 15x^2-11 x + \dfrac{121}{60} -\dfrac{1}{60}$

Donc, sous forme développée, $f(x)=15x^2-11 x + 2$ .

Réponse à la question 3 de maths sur les fonctions de référence en seconde

$\sqrt{12^3}$ et $\sqrt{13^3}$ puis

$\left((-2)^3\right)^2$ et $\left(\dfrac{3^2}{2^2}\right)^3$ .

Sachant que $12<13$ , on a:

Par la croissance de la fonction cube sur $\mathbb{R}$ ,

$12^3 < 13^3$ ;

Par la croissance de la fonction racine sur $]0;+\infty[$ ,

$\sqrt{12^3}<\sqrt{13^3}$ .

On rappelle que pour tout réel $x$ et pour tous entiers $n, m$ : $(a^m)^n=(a^n)^m=a^{m\times n}$

Sachant que $2>\dfrac{3}{2}$ , on a :

Par la croissance de la fonction carré sur $]0;+\infty[$ ,

$2^2>\left(\dfrac{3}{2}\right)^2$ ;

Par parité de la fonction carré, $(-2)^2>\dfrac{3^2}{2^2}$ ;

Par la croissance de la fonction cube sur $\mathbb{R}$ ,

$\left((-2)^2\right)^3 > \left(\dfrac{3^2}{2^2}\right)^3$ ;

Par la propriété rappelée ci-dessus,

$\left((-2)^3\right)^2 > \left(\dfrac{3^2}{2^2}\right)^3$ .

2. $\sqrt{\dfrac{1}{7}}$ et $\dfrac{1}{3}$ puis $\dfrac{1}{\sqrt{16^3}}$ et $\dfrac{1}{65}$ .

Sachant que $7<9$ , on a:

Par la croissance de la fonction racine carrée sur $]0;+\infty[$ ,

$\sqrt{7}<\sqrt{9}$ ;

Par la décroissance de la fonction inverse sur $]0;+\infty[$ ,

$\dfrac{1}{\sqrt{7}}>\dfrac{1}{\sqrt{9}}$ ;

Par conséquent, $\sqrt{\dfrac{1}{7}}>\dfrac{1}{3}$ .

D’abord, on a $\sqrt{16^3}=\sqrt{16^2\times 16}=\sqrt{16^2\times 4^2}$ . Donc, sous forme d’entier naturel, $\sqrt{16^3}=16 \times 4=64$ .

Sachant que $64<65$ , on a:

Par la décroissance de la fonction inverse sur $]0;+\infty[$ ,

$\dfrac{1}{64}>\dfrac{1}{65}$ ;

Par conséquent, $\dfrac{1}{\sqrt{16^3}}>\dfrac{1}{65}$ .

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

Corrigé du QCM 4 de maths sur les fonctions de référence en 2nde

Soit $x$ un réel tel que $-\dfrac{7}{4}>x>-\dfrac{13}{3}$ .

Par la décroissance de la fonction inverse sur $]-\infty;0[$ , on a :

$-\dfrac{7}{4}>x>-\dfrac{13}{3} \Longrightarrow -\dfrac{4}{7}<\dfrac{1}{x}<-\dfrac{3}{13}$

Ce qui donne, $-\dfrac{7}{4}>x>-\dfrac{13}{3}$ entraîne

$\dfrac{1}{x} \in \left] -\dfrac{4}{7};-\dfrac{3}{13} \right[$ .

Par la décroissance de la fonction carré sur $]-\infty;0[$ ,

On a : $-\dfrac{7}{4}>x>-\dfrac{13}{3} \Longrightarrow \left(-\dfrac{7}{4}\right)^2<x^2<\left(-\dfrac{13}{3}\right)^2$

Par la décroissance de la fonction inverse sur $]0;+\infty[$ ,

On a : $\dfrac{4^2}{7^2}>\dfrac{1}{x^2}>\dfrac{3^2}{13^2}$ .

Par conséquent, pour $-\dfrac{7}{4}>x>-\dfrac{13}{3},\ \dfrac{1}{x^2} \in \left] \dfrac{9}{169};\dfrac{16}{49} \right[$ .

Pour tout $x<0$ , $|x|=-x$ .

Alors, en multipliant $-\dfrac{7}{4}>x>-\dfrac{13}{3}$ par $-1$

On a : $\dfrac{7}{4}<-x<\dfrac{13}{3}$ .

Donc, $\dfrac{7}{4}<|x|<\dfrac{13}{3}$ .

Par la décroissance de la fonction inverse sur $]0;+\infty[$

On a : $\dfrac{4}{7}>\dfrac{1}{|x|}>\dfrac{3}{13}$

Puis en multipliant par $-1$ ,

On a : $-\dfrac{4}{7}<-\dfrac{1}{|x|}<-\dfrac{3}{13}$ .

Par conséquent, pour $-\dfrac{7}{4}>x>-\dfrac{13}{3},\ -\dfrac{1}{|x|} \in \left] \dfrac{4}{7};-\dfrac{3}{13} \right[$ .

Retrouvez plus d’exercices gratuits et corrigés en mathématique pour la seconde :

Exercices et corrigés sur les fonctions de référence en seconde

Exercice 1 de maths pour réviser les fonctions de référence en 2nde

Entrainement de seconde en maths pour réviser les fonctions de référence

Test 3 de maths niveau seconde sur les fonctions de référence

Question 4 en maths pour s’entrainer aux fonctions de référence en seconde

PARTICIPER À UN STAGE INTENSIF EN 2nde

Corrigé de l’exercice 1 sur les fonctions de référence en maths seconde

Correction du quiz 2 de mathématique pour comprendre les fonctions de référence en seconde générale

Réponse à la question 3 de maths sur les fonctions de référence en seconde

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Corrigé du QCM 4 de maths sur les fonctions de référence en 2nde

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Exercices et corrigés sur les fonctions de référence en seconde

Exercice 1 de maths pour réviser les fonctions de référence en 2nde

Entrainement de seconde en maths pour réviser les fonctions de référence

Test 3 de maths niveau seconde sur les fonctions de référence

Question 4 en maths pour s’entrainer aux fonctions de référence en seconde

PARTICIPER À UN STAGE INTENSIF EN 2nde

Corrigé de l’exercice 1 sur les fonctions de référence en maths seconde

Correction du quiz 2 de mathématique pour comprendre les fonctions de référence en seconde générale

Réponse à la question 3 de maths sur les fonctions de référence en seconde

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension clés de la réussite

Cours de maths en ligne ou à domicile

Corrigé du QCM 4 de maths sur les fonctions de référence en 2nde

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

La pratique et la compréhension
clés de la réussite