Mon parcours pour réussir en maths

J'aprends le cours par coeur

Je travaille avec un prof de maths

Je travaille entre chaque séance

Avis Google France
★★★★★ 4,8 sur 5

Exercices corrigés sur les statistiques descriptives en seconde

Résumé de cours Exercices et corrigés

Cours en ligne de Seconde Générale

Les exercices sur les statistiques descriptives représentent une opportunité exceptionnelle si vous souhaitez acquérir une compréhension profonde et pratique des données et de leur interprétation. Ces exercices ne sont pas seulement décisifs pour exceller en mathématiques, mais aussi pour développer des acquis analytiques. Pour renforcer votre niveau et assurer une compréhension plus profonde, l’engagement d’un cours de maths peut être très bénéfique. Un enseignement personnalisé en statistiques descriptives vous permet de se concentrer sur vos domaines de difficulté spécifiques, de surmonter les obstacles et de développer une base solide.

Notations sur les exercices sur les statistiques

Une population statistique est notée par $\Omega$ et le caractère étudié est noté généralement par $X$ .

Les valeurs prises par $X$ appelées modalités sont notées par $x_1,x_2,\dots, x_k$ où $k$ correspond au nombre des valeurs possibles.

$x_i$ la ième modalité du caractère étudié dans la population, $i=1,2,\dots,k$ ;

$n_i$ l’effectif associé à $x_i$ . C’est le nombre de fois où la valeur $x_i$ a été observée dans la population, $i=1,2,\dots,k$ ;

$m$ ou $\overline{X}$ la moyenne de la série $X$ ;

$Ecc$ est l’effectif cumulé croissant et $Ecd$ est l’effectif cumulé décroissant;

$M_e$ la médiane de la série $X$ ;

$Q_1$ le premier quartile et $Q_3$ le troisième quartile ;

$\sigma$ l’écart-type et $Var$ la variance.

Exercice 1 de maths sur l’analyse statistique des objets connectés en seconde

Une enquête auprès de 28 foyers a permis de recenser le nombre d’objets connectés appartenant aux membres de la famille.

Le tableau suivant résume les résultats :

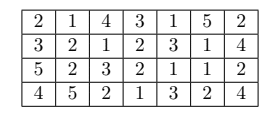
1. Préciser la population étudiée.

2. Préciser le caractère étudié.

3. Dresser un tableau des effectifs et des fréquences du caractère étudié.

Exercice 2 de maths : Répartition des enfants en charge dans les foyers en 2nde

Le tableau suivant donne la répartition de 160 foyers selon leurs nombres d’enfants en charge.

1. Déterminer l’écart inter-quartile et représenter la boîte à moustache de cette distribution.

2. Analyser la dispersion des foyers selon le nombre d’enfants en charge.

3. Déterminer la moyenne et l’écart-type de cette distribution. Interpréter les résultats.

4. Calculer le pourcentage des foyers qui ont :

a) au plus 3 enfants en charge.

b) moins 2 enfants en charge.

c) au moins trois enfants en charge.

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

Exercice 3 de maths programme python en seconde

On donne le programme en python suivant.

1. Qu’affiche ce programme ?

2. Combien y-a-t-il d’affectation pour la variable Total ?

3. Calculer la valeur reçue par la variable Somme après la troisième affectation.

4. Modifier ce programme à l’aide du conditionnel if pour ne calculer que la moyenne des valeurs positives.

Exercice 4 sur les implications des statistiques en seconde

Pour chacune des propositions suivantes, dire si ${P} \Rightarrow {Q}$ , ${Q} \Rightarrow {P}$ , ${P} \Leftrightarrow {Q}$ ou aucun des trois.

Démontrer votre réponse.

1. On considère une série d’observations $x_1,x_2,\dots,x_n$ .

P : Tous les $x_i$ pour $i$ allant de $1$ à $n$ sont égaux.

Q : La moyenne de la série est nulle.

2. On considère une série d’observations $x_1,x_2,\dots,x_n$ .

P : Tous les $x_i$ pour $i$ allant de $1$ à $n$ sont égaux.

Q : L’écart-type de la série est nul.

3. On considère une série statistique $x_1,x_2,\dots,x_n$ .

P : Le premier quartile, la médiane et le troisième quartile sont égaux.

Q : Toutes les valeurs de la série sont identiques.

4. On considère une série de nombres réels positifs rangée dans l’ordre croissant

$x_1,x_2,\dots,x_n$ , puis la série d’observations $-x_n,-x_{n-1}, \dots,-x_2,-x_1,x_1,x_2,\dots,x_n$

Donc le nombre d’observations vaut $2n$ avec $n\in \mathbb{N}$ .

P : L’écart-type est nul.

Q : L’écart interquartile $Q_3-Q_1$ est nul.

PARTICIPER À UN STAGE INTENSIF EN 2nde

C’est gagner des points sur ta moyenne !

Corrigé de l’exercice 1 sur l’analyse statistique des objets connectés en 2nde

1. La population est formée des 28 foyers.

2. Le caractère noté $X$ est le nombre d’objets connectés dans chaque famille.

Les modalités du caractère $X$ sont 1,2,3,4 et $5$ .

On les notera $x_1$ , $x_2$ , $x_3$ , $x_4$ et $x_5$ .

3. Pour $i\in \{1,2,3,4,5\}$ , la fréquence de la modalité $x_i$ est définie par $f_{i}=\dfrac{n_{i}}{n}$

Où $n_i$ est le nombre de fois où la valeur $x_i$ a été observée.

Ces informations sont résumées dans le tableau des effectifs et des fréquences de $X$ suivant :

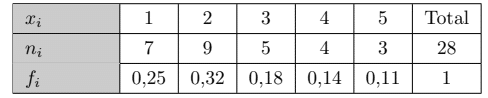
Réponse à l’exercice 2 : Répartition des enfants en charge dans les foyers en maths

Le tableau suivant donne les effectifs cumulés croissants des $160$ foyers.

1. Le premier quartile.

On a $\dfrac{n}{4} = \dfrac{160}{4} = 40$ .

Alors, $Q_{1}$ est la 40ème valeur.

Ainsi, $Q_{1}=1$ .

Le troisième quartile.

On a $\dfrac{3n}{4} = \dfrac{480}{4} = 120$ .

Alors, $Q_{3}$ est la 120ème valeur.

Ainsi, $Q_{3} = 3$ .

Sachant que les valeurs $Q_1$ et $Q_3$ ci-dessus,

On a :

L’écart inter-quartile $Q_{3}-Q_{1} = 3-1 = 2$ .

La médiane.

Sachant que $n = 160 = 2\times80$ .

Donc, $M_e = 2$ .

Voici le diagramme en boîte correspond :

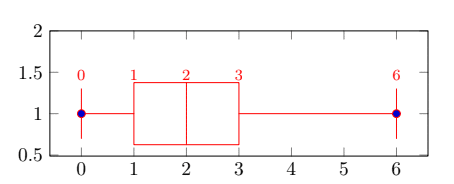
2. D’après les quartiles ci-dessus, on constate qu’au moins 50 % des foyers ont un nombre d’enfants compris entre 1 et 3.

3. On a :

$m=\dfrac{0\times18+1\times30+2\times50+3\times31+4\times20+5\times 9+6\times2}{160}$

= $\dfrac{360}{160}$

Ce qui donne $m=2,25$ .

$Var$

= $\dfrac{18\times0^{2}+30\times1^{2}+50\times2^{2}+31\times3^{2}+40\times4^{2}+9\times5^{2}+{2}\times6^{2}}{160}-\left( \dfrac{360}{160}\right)^{2}$

= $\dfrac{50560}{25600}$ .

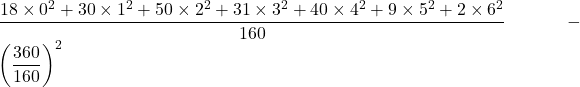
Or $\sigma=\sqrt{Var}$ .

Donc, $\sigma=\sqrt{\dfrac{50560}{25600}}\approx1,41$ .

Alors, en moyenne, un foyer compte 2,25 enfants et le nombre d’enfant s’écarte d’environ 1,41 de la moyenne.

4. Le nombre de foyers qui ont :

(a) au plus 3 enfants en charge est $18+30+50+31 = 129$ soit $80,63\,\%$ .

(b) moins de 2 enfants en charge est $18+30 = 48$ soit $30%$ .

Correction exercice3 sur le programme python en niveau seconde

1.Ce programme affiche la moyenne de la série dans la liste X pondérée par les effectifs dans la liste N.

2. La fonction len renvoie au nombre d’éléments dans la liste et la fonction range(a,b) renvoie au nombre entiers entre $a$ et $b-1$ où $a$ et $b$ sont des entiers.

Donc, il y a 8 affectations dans Total = Total+N[i].

La variable Total reçoit son ancienne valeur ajoutée du prochain effectif N[i].

Donc, à la fin de la boucle for, la variable Total reçoit l’effectif total.

3. Sur les trois premières affectations, les valeurs reçues par Somme sont :

Somme reçoit 0 + $-3\times 5$ , soit $-15$

Somme reçoit $-15$ + $6\times 10$ soit $45$

Somme reçoit $45$ + $8\times 25$ soit $245$

4. Dans la condition if, on exclut les valeurs strictement négatives de X.

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Corrigé exercice 4 : Les implications des statistiques en seconde

L’assertion ${P}$ implique l’assertion ${Q}$ mais la réciproque n’est pas vraie.

Soient $x_1, x_2, \dots, x_n$ les valeurs observées d’une série statistique notée $X$ .

${P} \implies {Q}$ . Par raisonnement direct.

Si, pour tout $i$ allant de 1 à $n$ , les $x_{i}=0$ alors $m=\dfrac{1}{n}(0+0+ \dots +0)$ . Ce qui donne $m=\dfrac{1}{n}\times 0$ .

Donc, la moyenne de cette série est nulle.

${Q} \nRightarrow {P}$ . Un contre-exemple.

On prend $x_1=1, x_2=2, x_3=-2, x_4=-1, x_5=0, \dots, x_n=0$ .

Alors, la moyenne $m=\dfrac{1}{n}(1+2-2-1+ \dots +0)=\dfrac{1}{n}(3-3)=0$ .

Donc, la moyenne de la série est nulle alors qu’il existe des valeurs de la série qui ne sont pas nulles (à l’occurrence $x_1, x_2, x_3$ et $x_4$ sont non-nuls).

Les assertions $\textbf{P}$ et $\textbf{Q}$ sont équivalentes.

On a une série statistique $x_1, x_2, \dots, x_n$ .

${P}\implies$ ${Q}$ . Par un raisonnement direct.

Soit $a\in \mathbb{R}$ et on suppose que pour tout $i$ allant de 1 à $n$ , les $x_{i}=a$ alors, $m=a$ .

Donc, l’écart-type de cette série est :

$\sigma=\sqrt{\dfrac{1}{n}\Big((x_1-m)^2+(x_1-m)^2+ \dots + (x_n-m)^2\Big)}$

$\sigma=\sqrt{\dfrac{1}{n}\Big((a-a)^2+(a-a)^2+ \dots + (a-a)^2\Big)}$ \par \noindent

$\sigma=\sqrt{\dfrac{1}{n}\times 0}=\sigma=\sqrt{0}$ . Donc, l’écart-type est nul.

${Q} \nRightarrow {P}$ . Par un raisonnement direct

On suppose que l’écart-type $\sigma = 0$ . Alors,

$\sigma^2 =\dfrac{1}{n}\underbrace{\Big((x_1-m)^2+(x_2-m)^2+\dots+(x_n-m)^2\Big)}_{somme\ de\ nombre\ positifs}=0$

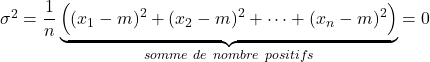
Or, si la somme de deux nombres positifs est nulle alors ces deux nombres sont nuls.

Cette propriété reste vraie pour une somme de plusieurs nombres.

Donc, pour tout $i$ allant de $1$ à $n$ , $(x_i-m)=0$ .

Ce qui donne, $x_i=m$ pour tout $i$ allant de $1$ à $n$ .

C’est-à-dire que les $x_i$ sont égaux.

L’assertion ${Q}$ implique ${P}$ mais ${P}$ n’implique pas ${Q}$ .

Soient $x_1, x_2, \dots, x_n$ les valeurs observées d’une série statistique.

${P} \nRightarrow {Q}$ . Un contre exemple.

On prend $x_1=0$ et pour tout $i>1$ , $x_i=1$ .

On suppose en outre que $n>4$ .

Premier quartile : On a $\dfrac{n}{4}>1$ . Donc, le premier quartile $Q_1=x_i$ avec $i>1$ . Soit, $Q_1=1$ .

Médiane = Deuxième quartile : On a $\dfrac{n}{2}>1$ .

Donc, le deuxième quartile $M_e=x_i$ avec $i>1$ . Soit, $M_e=1$ .

Troisième quartile : On a $3\times \dfrac{n}{4}>1$ .

Donc, le troisième quartile $Q_3=x_i$ avec $i>1$ . Soit, $Q_3=1$ .

Ainsi, on a $Q_1=M_e=Q_3 =1$ alors que les valeurs observées ne sont pas toutes identiques.

${Q} \Longrightarrow$ ${P}$ . Par un raisonnement direct.

Soit $a\in \mathbb{R}$ et on suppose que pour tout $i$ allant de $1$ à $n$ , $x_i=a$ .

Les valeurs des $x_i$ sont identiques.

Comme $M_e=x_i$ pour un certain $i$ , alors $M_e=a$ .

De même, $Q_1=x_i$ pour un certain $i$ et $Q_3$ aussi. Alors, $Q_1=M_e=Q_3 =a$ .

L’ assertion $\textbf{P}$ entraîne l’assertion ${Q}$ , mais la réciproque est fausse.

Quelles que soient des valeurs prises par $x_i$ , la moyenne $m=0$ .

Car, pour tout $i$ allant de $1$ à $n$ , $x_i$ et $-x_i$ s’annulent dans la somme pour calculer la moyenne.

${P} \Longrightarrow$ ${Q}$ . Par un raisonnement direct.

Si l’écart-type $\sigma=0$ alors la variance

$\sigma^2=\dfrac{1}{n}\Big((x_1-0)^2+(x_2-0)^2+\dots+(x_n-0)^2\Big)$

C’est une somme de nombres positifs, alors pour tout $i$ ,

$(x_i-m=0)$ . Donc, pour $i$ allant de $1$ à $n$ , $x_i=m=0$ .

Par conséquent, le premier et le troisième quartile sont nuls.

Donc, l’écart inter-quartile $Q_3-Q_1=0$ .

${Q} \nRightarrow$ ${P}$ . Par un raisonnement direct.

Les valeurs observées de la série sont symétriques par rapport à $0$ .

Donc, le premier et le troisième quartile ont la même valeur absolue et de signes opposés.

Par conséquent, $Q_1=-Q_3$ . Ce qui donne l’écart inter-quartile $Q_3-Q_1=Q_3-(-Q_3)=Q_3+Q_3=2Q_3=0$ .

Ainsi, il suffit de prendre $n>4$ et $x_i=0$ pour tout $i$ sauf pour le dernier $x_n\neq 0$ .

Dans ce cas, l’écart interquartile est nul mais l’écart-type n’est pas nul.

Consultez nos exercices en ligne de maths en seconde générale :

Exercices corrigés sur les statistiques descriptives en seconde

Exercice 1 de maths sur l’analyse statistique des objets connectés en seconde