Chapitres de maths en 1ère

Exercices sur le second degré en première

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Première

Ces exercices sur le second degré permettent aux élèves de réviser ce chapitre important en classe de première. Les élèves ne doivent pas hésiter à travailler sur d’autres chapitres avec les cours en ligne de maths en première comme les exercices sur les suites numériques par exemple, les exercices sur les séries arithmétiques et géométriques, les exercices sur la dérivation ou encore sur le chapitre des probabilités et statistiques. Vous pouvez aussi prendre des cours de maths à domicile pour pallier vos lacunes et améliorer votre niveau en maths en première.

Second degré : exercice 1

Résoudre $\sqrt{2\, x + 1} - 2 =3\, x$

Second degré : exercice 2

On suppose que $a \neq 0$ et que $u$ et $v$ sont les racines de $\qquad Q(x) = a\, x ^2 + b \, x + c = 0$

$\displaystyle \frac 1 {u ^2} + \frac 1 {v ^2 }$ est égal à :

1. $\displaystyle \frac {b ^2 - 2\, a \, c} {c ^2 }$

2. $\displaystyle \frac {b ^2 - 4\, a \, c} {c ^2 }$ ?

Second degré : exercice 3

Existe-t-il un couple d’entiers consécutifs dont le produit est le double de la somme ?

Second degré : exercice 4

Soit $m \in \mathbb{R}$ , étudier le nombre de solutions réelles de l’équation $(E)$

$(m - 4) \, x^2 - 2(m -2) \, x + 2\, m - 3 = 0$

Second degré : exercice 5

Résoudre

$\qquad \displaystyle \frac {1} {x - 1} + \frac 1 {2\, x- 3} \leqslant \frac {6} {6\, x - 7}$

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 1 sur le second degré

Pour que la racine carrée soit définie, on suppose que $2 \, x + 1 > 0$ ssi $x > - 1/2$ .

On écrit l’équation sous la forme

$\qquad \sqrt{2\, x + 1} = 3\, x + 2$ .

Lorsque $x \geqslant - 1/2$ , les deux membres de l’équation sont positifs ou nuls (car $3\, x + 2 \geqslant 1/2$ ), donc l’équation $a = b$ est équivalente à $a^2 = b ^2$

ssi $2 \, x + 1 = (3\, x + 2) ^2$

ssi $9 \, x ^2 + 12\, x + 4 = 2\, x + 1$

ssi $9\, x ^2 + 10 \, x + 3 = 0$ .

Le discriminant de l’équation est égal à $\Delta = 100 - 12 \times 9 = 100 - 108 = - 8 < 0$

L’équation n’admet pas de solution.

Correction de l’exercice 2 sur le second degré

$E = \displaystyle \frac 1 {u ^2} + \frac 1 {v ^2 } = \displaystyle \frac {u ^2 + v^2} {u ^2 \, v ^2}$

$u \, v$ est le produit des racines de l’équation donc $u \, v = \displaystyle \frac {c} a$ .

$u ^2 + v^2 = (u + v)^2 - 2\, u \, v$

$u + v$ est la somme des racines de l’équation donc $u + v = \displaystyle \frac {- b} a$

$u ^2 + v^2 = \displaystyle \frac { b ^2} {a^2} - \frac {2\, c} a = \frac {b ^2 - 2 \, a \, c} {a ^2}$

$\boxed{E = \displaystyle \frac {b ^2 - 2\, a \, c} {c ^2 }}$ .

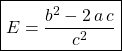Correction de l’exercice 3 sur le second degré

On cherche un entier $x$ tel que $S = x + x + 1 = 2\, x + 1$ et $P = x( x + 1)$ vérifient $P = 2\, S$

ssi $x (x + 1) = 2 (2\, x + 1)$

ssi $x^2 + x - 4 \, x - 2 = 0$

ssi $x ^2 - 3 \, x - 2 = 0$

$\Delta = 9 + 8 = 17$ .

Cette équation n’admet pas de solution entière.

Le problème n’a pas de solution, la réponse est donc non.

Correction de l’exercice 4 sur le second degré

$\bullet$ Si $m = 4$ , l’équation s’écrit

$\qquad \qquad \qquad - 4\, x + 5= 0$ , elle admet une unique solution.

$\bullet$ Si $m \neq 4$ , l’équation est du second degré de discriminant

$\Delta = 4\,(m - 2)^2 - 4\,(m - 4)(2\, m - 3)$

$\Delta = 4\, (m ^2 - 4\, m + 4)$ $\qquad \qquad - \, 4\,(2 \, m ^2 - 8\, m - 3\, m + 12)$

$\Delta = 4\, (- m ^2 +7 \, m - 8)$ .

On cherche les racines de $\qquad \quad - m ^2 +7 \, m - 8 = 0$ .

Le discriminant $\Delta' = 49 - 4 \times 8 = 17$

$\Delta = 0$ admet deux racines

$\qquad m_1 = \displaystyle \frac {- 7 - \sqrt{17}} {- 2} = \frac {7 + \sqrt{17}} 2$

$\quad$ et $m_2 = \displaystyle \frac {- 7 + \sqrt{17}} {- 2} = \frac {7 - \sqrt{17}} 2$

avec $m_2 < m_1\,$ .

$\ast$ Si $m < m_2$ ou $m > m_1\,$ , $\Delta < 0$ , l’équation $(E)$ n’admet pas de solution.

$\ast$ Si $m = m_1$ ou $m = m_2\,$ , l’équation $(E)$ admet une racine double.

$\ast$ Si $m_2 < m < m_1\,$ , l’équation $(E)$ admet deux racines distinctes.

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 5 sur le second degré

On suppose que $x \in \mathcal{D}$ où $\qquad \mathcal{D} = \mathbb{R} \setminus \{ 1\, , \, 3/2 \, , \, 7/6\}$ .

L’inéquation est équivalente à $f(x) \geqslant 0$ avec $f(x) = \displaystyle \frac {6} {6\, x - 7} - \frac {1} {x - 1} - \frac 1 {2\, x- 3}$

On réduit au même dénominateur

$f(x) = \displaystyle \frac {N(x)} {D(x)}$

avec $D(x) = (6 \, x - 7) (2\, x - 3) (x - 1)$

et $N(x) = 6(x - 1)(2\, x - 3)$ $\qquad -\, (6\, x - 7)(x - 1) - (6\, x - 7)(2\, x - 3)$

$N(x) = 6\,(x - 1)(2\, x - 3)$ $\qquad \qquad - \, (6\, x - 7)(x - 1 + 2\, x - 3)$

$= 6\, (2\, x ^2 - 5\, x + 3) - (6\, x - 7) (3\, x - 4)$

$= 12\, x^2 - 30 \, x + 18 - (18\, x^2 - 45\, x + 28)$

$N(x) = - 6\, x ^2 + 15\, x - 10$ .

Le discriminant de $N$ est égal à $\qquad \Delta = 15^2 - 24 \times 10 = - 15 < 0$

donc $N(x)$ est du signe du coefficient de $x ^2$ soit $N(x) < 0$ .

On en déduit que $f(x) \geqslant 0$ ssi $D(x) < 0$

Les racines de $D$ rangées par ordre strictement croissant sont $1 ,\, \displaystyle \frac 7 6 , \, \frac 3 2$ .

Je vous laisse faire un tableau de signes pour démontrer que

$D(x) < 0$ ssi $x < - 1$ ou $7/6 < x < 3/2$

L’ensemble des solutions est $\qquad \quad \displaystyle \boxed {]- \infty - 1[\; \cup\; \left ] \frac 7 6 ,\, \frac 3 2 \right [}$ .

👍 On fera attention dans le cas d’inégalités faisant intervenir des fractions dépendant de $x$ de ne pas faire le « produit en croix » , il faut penser à faire attention au signe des dénominateurs.

Le plus simple est donc de se ramener à une inégalité du type $f(x) > 0$ ou $f(x) \geqslant 0$ et d’étudier le signe du numérateur $N(x)$ et du dénominateur $D(x)$ .

On pourra si nécessaire introduire un tableau de signes.

On peut aussi dire que

$\displaystyle \frac {N(x)} {D(x)} > 0$ ssi $N(x) \, D(x) > 0$

$\displaystyle \frac {N(x)} {D(x)} \geqslant 0$ ssi $N(x) \, D(x) \geqslant 0$ et $D(x) \neq 0$ .

L’application mobile PrepApp contient d’autres exercices sur le second degré en première et sur les autres chapitres de maths (exercices sur la fonction exponentielle par exemple). Les élèves peuvent aussi travailler sur ces chapitres avec un professeur de maths particulier.