Chapitres de maths en Terminale D

Cours sur les probabilités en Terminale D

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1012 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de maths en Terminale D

Vous trouverez ci-dessous un cours de maths sur les probabilités proposé aux élèves de terminale D. Ce chapitre est un des plus importants de l’année de terminale pour le bac et pour la préparation des études supérieures en mathématiques. Des professeurs particuliers en maths en ligne sont disponibles si vous souhaitez un accompagnement plus important.

1 – Conditionnement et indépendance en terminale D

Définition : probabilité conditionnelle

Soient des événements $A$ et $B$ . Si $A$ est de probabilité non nulle, alors la probabilité de $B$ sachant $A$ , notée $P_{A}(B)$ , est définie par :

${P_{A}(B)=\dfrac{P(A \cap B)}{P(A)}$

Définition : événements indépendants

Des événements $A$ et $B$ sont dits indépendants si et seulement si ${P(A \cap B) = P(A) \times P(B)$ .

Théorème

Soient des événements $A$ et $B$ de probabilités non nulles. Les trois assertions suivantes sont équivalentes :

(i) $P_{A}(B)=P(B)$

(ii) $P(A \cap B) = P(A) \times P(B)$

(iii) $P_{B}(A)=P(A)$

Définition : indépendance de $2$ variables aléatoires

Soient $2$ variables aléatoires $X$ et $Y$ définies sur $E$ .

On note $x_{1}, x_{2},..., x_{k}$ les valeurs prises par $X$ et $y_{1}, y_{2},...,y_{r}$ celles prises par $Y$ .

$X$ et $Y$ sont dites indépendantes si et seulement si, pour tout $i$ de $\{1,2,...,k\}$ et tout $j$ de $\{1,2,...,r\}$ :

$P(X=x_{i}$ et $Y=y_{j})$

$= P(X=x_{i}) \times P(Y=y_{j})$

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

2 – Combinaisons en probabilité en terminale D

Définition

Soit $E$ un ensemble de cardinal $n$ , soit $p$ un entier naturel

$\bullet$ Une combinaison de $p$ éléments de $E$ est une partie de $E$ possédant $p$ éléments. On note $\begin{pmatrix} n \\ p \\ \end{pmatrix}$ le nombre de combinaisons de $p$ éléments de $E$ .

$\bullet$ Si $p=0$ , alors $\begin{pmatrix} n \\ 0 \\ \end{pmatrix} = 1$ .

$\bullet$ Si $0 < p \leq n$ , alors : $\begin{pmatrix} n \\ p \\ \end{pmatrix} = \displaystyle{\frac{n (n-1)\times ... \times (n-p+1)}{p (p-1) \times ... \times 2 \times 1}}$

= $\displaystyle{\frac{n!}{p!(n-p)!}}$ .

Propriétés

$\bullet$ Pour tout entier naturel $n$ : $\begin{pmatrix} n \\ 0 \\ \end{pmatrix} = \begin{pmatrix} n \\ n \\ \end{pmatrix} = 1$ et si $n \geq 1$ : $\begin{pmatrix} n \\ 1 \\ \end{pmatrix} = \begin{pmatrix} n \\ n-1 \\ \end{pmatrix} = n$ .

Pour tous entiers naturels $n$ et $p$ tels que $p \leq n$ , on a : $\begin{pmatrix} n \\ p \\ \end{pmatrix} = \begin{pmatrix} n \\ n-p \\ \end{pmatrix}$ .

Formule de Pascal : pour tous entiers naturels $n$ et $p$ tels que $p < n$ , on a :

${\begin{pmatrix} n+1 \\ p+1 \\ \end{pmatrix} = \begin{pmatrix} n \\ p \\ \end{pmatrix} + \begin{pmatrix} n \\ p+1 \\ \end{pmatrix}$

Formule du binôme de Newton

Pour tous complexes (et donc réels) $a$ et $b$ , et tout entier naturel non nul $n$ :

$(a+b)^{n}$ =

$a^{n} + \begin{pmatrix} n \\ 1 \\ \end{pmatrix} a^{n-1}b^{1} + ... + \begin{pmatrix} n \\ k \\ \end{pmatrix} a^{n-k}b^{k} + ... + \begin{pmatrix} n \\ n-1 \\ \end{pmatrix} a^{1}b^{n-1} + b^{n} = \sum_{k=0}^{n} \begin{pmatrix} n \\ k \\ \end{pmatrix} a^{n-k}b^{k}$

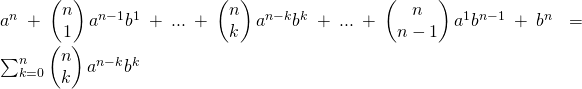
COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

3 – Lois de probabilités discrètes terminale D

Loi de Bernoulli

Une variable aléatoire $X$ , prenant la valeur $1$ avec la probabilité $p$ et la valeur $0$ avec la probabilité $1-p$ , suit la loi de Bernoulli de paramètre $p$ .

On notera alors :

${X \thicksim B(p)$

L’espérance et la variance d’une variable aléatoire de Bernoulli de paramètre $p$ sont données par :

${E(X)=p\text{ et }Var(X)=p(1-p)$

Loi binomiale

La somme $X$ de $n$ variables aléatoires indépendantes de Bernoulli, prenant la valeur $1$ avec la probabilité $p$ et la valeur $0$ avec la probabilité $1-p$ , suit la loi binomiale de paramètre $(n,p)$ .