Cours d’optique sur les images et couleurs en 1ère

Résumé de cours Exercices et corrigés

Cours en ligne de physique en Première

Ce cours en ligne de physique chimie en première vous servira pour travailler le cours d’optique de spécialité sur les images et couleurs. Vous retrouverez notamment les éléments suivants : Image d’un objet par une lentille convergente, relations algébriques et couleurs. Si vous souhaitez vous faire accompagner, n’hésitez pas à consulter nos cours particuliers de physique chimie. Nos professeurs particuliers en 1ère pourront vous aider à mieux appréhender ces notions importantes en première et terminale pour le bac.

Vous pouvez consulter d’autres résumés de cours de physique chimie en première sur notre site : évolution d’un système chimique, dosage colorimétrique, structure des espèces chimiques, etc.

Image d’un objet par une lentille convergente en 1ère

Rappels sur la lentille mince convergente

* Elle est modélisée par une double flèche perpendiculaire à l’axe optique passant par son centre

* Tout rayon lumineux passant par n’est pas dévié

* Tout rayon incident parallèle à l’axe optique, après traversée de la lentille, en ressort en passant par le foyer image

* Tout rayon incident passant par le foyer objet , après traversée de la lentille, en ressort parallèle à l’axe optique.

* Le centre optique est le milieu du segment

* La distance est la distance focale de la lentille convergente.

Construction de l’image d’un objet

Un objet est modélisé par une flèche perpendiculaire à l’axe optique, étant pris sur l’axe optique et au dessus.

Si l’objet est une source de lumière, ou s’il est éclairé, il émet ou il diffuse de la lumière, modélisée par un ensemble de rayons lumineux partant de chacun de ses points.

En particulier, on considère l’ensemble des rayons issus de .

Parmi ceux-ci :

* le rayon parallèle à l’axe ressort en passant par

* le rayon passant par le centre n’est pas dévié

* le rayon passant par ressort parallèle à l’axe.

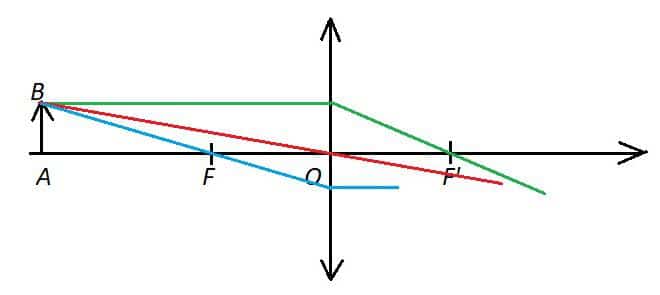
Trois cas sont possibles.

Premier cas. Si est à gauche de

Dans ce cas, les trois rayons convergent vers un point unique , et on démontre que tous les autres rayons issus de convergent vers ce même point

est appelé le point conjugué de

Si on place un écran dans le plan orthogonal à l’axe optique passant par ce point , alors l’image du point est le point

On démontre qu’il en est de même de tous les autres points de l’objet, et du point dont les rayons convergent vers le point situé sur l’axe.

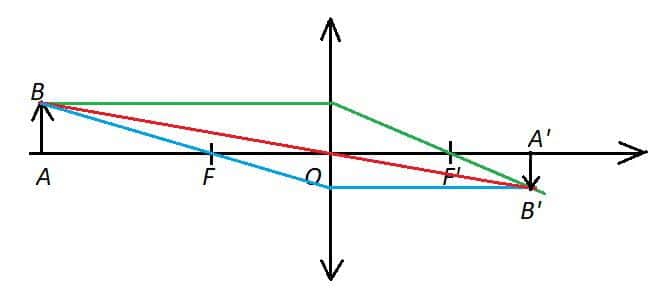
On observe dans ce cas sur l’écran une image nette de l’objet

Cette image, qu’on peut former sur un écran situé à droite de la lentille, est une image réelle et inversée.

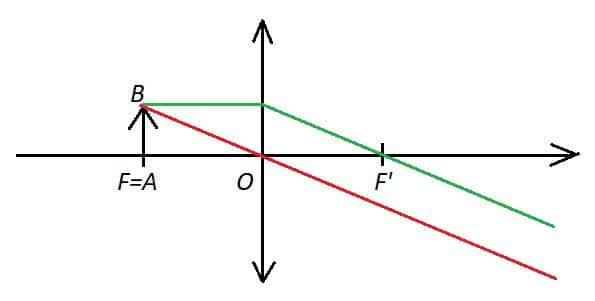
Deuxième cas. Si est confondu avec , c’est-à-dire que l’objet est dans le plan focal objet de la lentille

Dans ce cas, le rayon passant par est exclu, et les deux autres rayons issus de sortent parallèles entre eux de la lentille. Ils ne se croisent donc pas.

En revanche, un observateur situé à droite de la lentille a l’impression que ces deux rayons viennent de l’infini, ce qui lui permettra une vision confortable.

On dit que l’image est à l’infini.

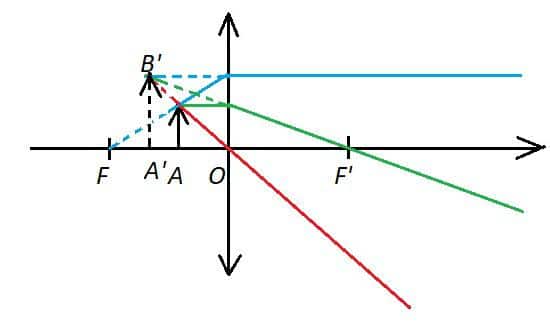
Troisième cas. est situé entre et

Dans ce cas, le troisième rayon issu de ne passe pas par mais semble provenir de

Les trois rayons sortant de la lentille ne se croisent pas à droite de la lentille, il n’est donc pas possible de former l’image sur un écran.

En revanche, un observateur situé à droite de la lentille perçoit les trois rayons qui, si on les prolonge à gauche de la lentille, semblent provenir d’un même point

On démontre que les rayons issus de semblent provenir d’un point situé dans le même plan orthogonal à l’axe optique que

Il voit donc réellement une image droite et virtuelle. On la trace en pointillés.

Exemple : Molécules d’eau dans un litre d’eau

Combien y a-t-il de molécules d’eau dans 1 litre d’eau, représentant environ d’eau ?

Corrigé de l’exemple : molécules.

Applications pratiques

* Dans le premier cas, on forme sur un écran une image réelle et nette d’un objet lumineux. C’est le principe de la lentille de projection, utilisée dans les rétroprojecteurs, les vidéoprojecteurs, les projecteurs de film et de diapositive. Notons que l’image étant inversée, il faut que l’objet soit « à l’envers » pour que l’image soit « à l’endroit ». C’est aussi ce qui se passe dans le cas de l’œil, où la lentille convergente s’appelle le cristallin et l’écran la rétine.

* Dans le deuxième cas, on forme une image à l’infini d’un objet, rendant la vision confortable pour l’observateur. C’est le principe de l’oculaire, utilisé dans les microscopes, où l’image d’un objet très petit par une première lentille (l’objectif) devient elle-même l’objet pour la deuxième lentille, l’oculaire, donnant une image finale à l’infini.

* Dans le troisième cas, on obtient une image droite, virtuelle, et on démontre qu’elle est à gauche et plus grande que l’objet. C’est le principe de la loupe. Un observateur situé à droite de la lentille voit une image plus grande et plus lointaine que l’objet.

Cours sur les images et couleurs 1ère : Relations algébriques

Principe et grandeurs algébriques

La construction géométrique de l’image par une lentille peut être traduite par des relations algébriques en utilisant les relations de Thalès et de Chasles.

Dans une grande majorité d’exercices d’optique géométrique, on fait la construction à l’échelle, on calcule les grandeurs métriques et on vérifie la cohérence des résultats. On en déduit l’utilité du dispositif.

Pour définir les grandeurs métriques, on définit sur l’axe optique (horizontal sur la figure) et sur l’axe perpendiculaire un sens conventionnel, vers la droite et vers le haut.

* Soient deux points et sur l’axe optique. La mesure algébrique est un nombre réel positif si est orienté dans le sens positif ( à gauche de ), négatif sinon ( à droite de ), et dont la valeur absolue est égale à la distance entre et

* Soient deux points et sur l’axe perpendiculaire. La mesure algébrique est un nombre réel positif si est orienté dans le sens positif ( en-dessous de ), négatif sinon ( au-dessus de ), et dont la valeur absolue est égale à la distance entre et

Distance focale et vergence

Retrouvez cette partie de cours sur la distance focale et vergence dans notre application mobile gratuite PrepApp à télécharger sur Google play ou Apple store.

Relation de conjugaison de Descartes.

Cette partie de résumé de cours sur la relation de conjugaison de Descartes est à retrouver dans l’appli mobile PrepApp.

Grandissement

Lorsqu’une lentille convergente donne d’un objet une image , le grandissement est le rapport

C’est un nombre réel positif dans le cas d’une image droite, négatif dans le cas d’une image inversée, sans dimension.

On a démontré au paragraphe précédent qu’on pouvait aussi donner l’expression

Images et couleurs : Couleurs

1. Spectre de la lumière blanche.

La lumière blanche est composée d’une infinité de radiations correspondant à autant de nuances de couleurs.

Consultez les parties de résumés de cours suivantes en téléchargeant notre application mobile PrepApp :

2. Synthèse additive

3. Synthèse soustractive

Retrouvez d’autres cours en ligne gratuits en 1ère sur notre site :

• Cours sur l’interaction et champs pour la première
• Résumé de cours sur les statiques des fluides
• Cours sur les mouvements et forces en 1ere
• Résumé de cours sur les aspects énergétiques des phénomènes électrique en première
• Cours sur le théorème de l’énergie cinétique en 1ère