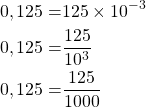Mon parcours pour réussir en maths
J'aprends le cours par coeur
Je travaille avec un prof de maths
Je travaille entre chaque séance
Avis Google France
★★★★★ 4,8 sur 5
Cours sur les nombres réels, ensembles et intervalles
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Seconde générale
Entiers naturels et nombres réels : définitions
- Définition : Appartenance
On considère un ensemble E. On dit que x est un élément de E si x appartient à l’ensemble E. On note alors : ![]() .
.
- Définition : ensembles de nombres
![]() L’ensemble des entiers naturels est l’ensemble des nombres : 0, 1, 2, … On le note
L’ensemble des entiers naturels est l’ensemble des nombres : 0, 1, 2, … On le note ![]() :
: ![]() = {
= {![]() }
}
![]() L’ensemble des entiers relatifs est l’ensemble composé des entiers naturels et de leur opposés. On le note
L’ensemble des entiers relatifs est l’ensemble composé des entiers naturels et de leur opposés. On le note ![]() :
:
![]() = {
= {![]() }
}
![]() L’ensemble des nombres décimaux est l’ensemble de tous les nombres qui s’écrivent sous la forme
L’ensemble des nombres décimaux est l’ensemble de tous les nombres qui s’écrivent sous la forme ![]() , où a et n sont deux entiers relatifs.
, où a et n sont deux entiers relatifs.
On le note ![]() . C’est l’ensemble des nombres à virgule à écriture finie.
. C’est l’ensemble des nombres à virgule à écriture finie.
![]() = {
= {![]() ,
, ![]() ,
, ![]() }
}
![]() L’ensemble des nombres rationnels est l’ensemble de tous les nombres pouvant s’écrire sous la forme
L’ensemble des nombres rationnels est l’ensemble de tous les nombres pouvant s’écrire sous la forme ![]() , où a et b sont deux entiers relatifs, avec
, où a et b sont deux entiers relatifs, avec ![]() . On le note Q :
. On le note Q :
![]() = {
= {![]() avec
avec ![]() ,
, ![]() ,
, ![]() }
}
- Exemple :
Déterminer une écriture sous la forme ![]() avec
avec ![]() et
et ![]() de 0,125 parmi les réponses suivantes :
de 0,125 parmi les réponses suivantes :
a. ![]()
b. ![]()
c. ![]()
- Réponse :
- On a :

D’où, sous la forme ![]() ,
, ![]() avec
avec ![]() et
et ![]()
b) Représentation de ces ensembles
L’ensemble des réels : l’ensemble des nombres réels est représenté par une droite graduée où l’on peut renseigner tout nombre réel.
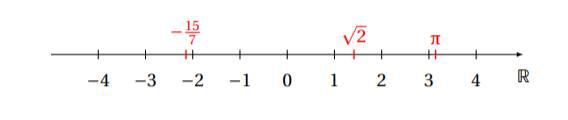
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Diagramme de Venn
Définition : inclusion
Soient E et F deux ensembles. Si tous les éléments de F sont aussi dans E, alors on dit que F est inclus dans E, et on note :

- Quelques propriétés :
![]() Tous les nombres rationnels sont aussi des nombres réels, donc
Tous les nombres rationnels sont aussi des nombres réels, donc ![]() .
.
![]() Tous les nombres décimaux sont aussi des nombres rationnels, donc
Tous les nombres décimaux sont aussi des nombres rationnels, donc ![]() .
.
![]() Tous les entiers naturels sont aussi des entiers relatifs, donc
Tous les entiers naturels sont aussi des entiers relatifs, donc ![]() .
.
![]() Tous les entiers relatifs sont aussi des nombres décimaux, donc
Tous les entiers relatifs sont aussi des nombres décimaux, donc ![]() .
.
On a alors :
![]() .
.
Ceci est représenté par le diagramme de Ven suivant :

Définition Intervalles
Soient ![]() et
et ![]() deux nombres réels tels que
deux nombres réels tels que ![]() <
< ![]() .
.
Définition : Intervalle fermé
On notera [![]() ;
; ![]() ] l’ensemble des nombres réels compris entre
] l’ensemble des nombres réels compris entre ![]() et
et ![]() . Ici,
. Ici, ![]() et
et ![]() sont compris dans l’intervalle car les crochets sont dirigés vers l’intérieur.
sont compris dans l’intervalle car les crochets sont dirigés vers l’intérieur.
On dira que [![]() ;
; ![]() ] est un intervalle fermé.
] est un intervalle fermé.
-
- Exemple 1
On représentera [−4 ; 3] ainsi :

Définition : Intervalle ouvert
On notera ]![]() ;
; ![]() [ l’ensemble des nombres compris entre
[ l’ensemble des nombres compris entre ![]() et
et ![]() , avec
, avec ![]() et
et ![]() qui ne sont pas compris dans l’intervalle car les crochets sont dirigés vers l’extérieur.
qui ne sont pas compris dans l’intervalle car les crochets sont dirigés vers l’extérieur.
On dira que [![]() ;
; ![]() ] est un intervalle ouvert
] est un intervalle ouvert
-
- Exemple 2
On représentera ]−4 ; 3[ ainsi :

Définition : Intervalle semi-ouvert à gauche
On notera ]![]() ;
; ![]() ] l’ensemble des nombres compris entre
] l’ensemble des nombres compris entre ![]() et
et ![]() , avec
, avec ![]() non compris dans l’intervalle (car le crochet est dirigé vers l’extérieur du côté de
non compris dans l’intervalle (car le crochet est dirigé vers l’extérieur du côté de ![]() ) et
) et ![]() compris dans l’intervalle (car le crochet est dirigé vers l’intérieur du côté de
compris dans l’intervalle (car le crochet est dirigé vers l’intérieur du côté de ![]() ).
).
-
- Exemple 3
On représentera ]−3 ; 4] ainsi :

Définition : Intervalle semi-ouvert à droite
On notera [a ; ![]() [ l’ensemble des nombres compris entre
[ l’ensemble des nombres compris entre ![]() et
et ![]() , avec
, avec ![]() compris dans l’intervalle (car le crochet est dirigé vers l’intérieur du côté de
compris dans l’intervalle (car le crochet est dirigé vers l’intérieur du côté de ![]() ) et
) et ![]() non compris dans l’intervalle (car le crochet est dirigé vers l’extérieur du côté de
non compris dans l’intervalle (car le crochet est dirigé vers l’extérieur du côté de ![]() ).
).
-
- Exemple 4
On représentera [−3 ; 4[ ainsi :

Définition : Intervalle infini
On notera ]−∞ ; ![]() [ l’ensemble des nombres strictement plus petits que
[ l’ensemble des nombres strictement plus petits que ![]() .
.
On notera ]−∞ ; ![]() ] l’ensemble des nombres plus petits que
] l’ensemble des nombres plus petits que ![]() ou égaux à
ou égaux à ![]() .
.
On notera ] ![]() ; +∞[ l’ensemble des nombres strictement plus grands que
; +∞[ l’ensemble des nombres strictement plus grands que ![]() .
.
On notera [![]() ; +∞[ l’ensemble des nombres plus grands que
; +∞[ l’ensemble des nombres plus grands que ![]() ou égaux à
ou égaux à ![]() .
.
Appartenance à un intervalle
Pour écrire qu’un nombre x appartient à un intervalle [![]() ;
; ![]() ], on écrira :
], on écrira :
![]()
![]() [
[![]() ;
; ![]() ].
].
Cela signifie que ![]() est compris entre
est compris entre ![]() et
et ![]() et on pourra donc l’écrire aussi :
et on pourra donc l’écrire aussi :
![]()
![]()
![]()
![]()
![]() .
.
Les signes strictes ou larges des inégalités sont choisis en fonction du sens des crochets de l’intervalle :
![]()
![]() [
[![]() ;
; ![]() ]
] ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ]
]![]() ;
; ![]() [
[ ![]()
![]() <
< ![]() <
< ![]()
![]()
![]() ]
]![]() ;
; ![]() ]
] ![]()
![]() <
< ![]()
![]()
![]()
![]()
![]() [
[![]() ;
; ![]() [
[ ![]()
![]()
![]()
![]() <
< ![]()
![]()
![]() [
[![]() ; +∞[
; +∞[ ![]()
![]()
![]()
![]()
![]()
![]() ]−∞ ;
]−∞ ; ![]() [
[ ![]()
![]() <
< ![]()
-
- Exemple
Comment s’écrit sous la forme ![]() l’intervalle suivant:
l’intervalle suivant:
![]()
a) ![]()
b) ![]()
c) ![]()
d) ![]()
On rappelle que :
![]()
![]() [
[![]() ;
; ![]() [
[ ![]()
![]()
![]()
![]() <
< ![]()
Union et intersection d’intervalles
Pour écrire qu’un nombre ![]() appartient à un intervalle [
appartient à un intervalle [![]() ;
; ![]() ] ou à un intervalle [
] ou à un intervalle [![]() ;
; ![]() ], on écrira :
], on écrira : ![]()
![]() [
[![]() ;
; ![]() ]
]![]() [
[![]() ;
; ![]() ].
].
On représentera l’union ainsi :

Pour écrire qu’un nombre ![]() appartient à un intervalle [
appartient à un intervalle [![]() ;
; ![]() ] et à un intervalle [
] et à un intervalle [![]() ;
; ![]() ], on écrira :
], on écrira : ![]()
![]() [
[![]() ;
; ![]() ]∩[
]∩[![]() ;
; ![]() ].
].
![]() Si les deux intervalles ne se chevauchent pas, l’intersection est vide (n’existe pas). On notera alors : [
Si les deux intervalles ne se chevauchent pas, l’intersection est vide (n’existe pas). On notera alors : [![]() ;
; ![]() ]∩[
]∩[![]() ;
; ![]() ] = ∅.
] = ∅.
![]() Si les deux intervalles se chevauchent, l’intersection est l’ensemble en commun aux deux intervalles :
Si les deux intervalles se chevauchent, l’intersection est l’ensemble en commun aux deux intervalles :
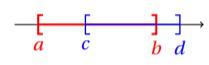
et est équivalente à :
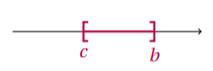
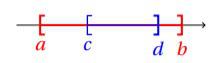
Inclusion d’intervalles
Si un intervalle [![]() ;
; ![]() ] est inclus dans un autre intervalle [
] est inclus dans un autre intervalle [![]() ;
; ![]() ], on écrira :
], on écrira :
Cela se schématise de la façon suivante :
Notations supplémentaires
L’ensemble des nombres réels auquel on enlève le nombre 0 est noté : ![]() ou
ou ![]() \ {0}.
\ {0}.
L’ensemble des nombres réels auquel on enlève le nombre a est noté : ![]() \ {
\ {![]() }.
}.
De plus, on notera :
]−∞ ; 0] = ![]() ;
;
]−∞ ; 0[ = ![]() ;
;
]0 ; +∞[ = ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Définition valeur absolu d’un nombre réel
Soit ![]() un nombre réel. On appelle valeur absolue de
un nombre réel. On appelle valeur absolue de ![]() la distance qui sépare
la distance qui sépare ![]() de 0 sur la droite des réels.
de 0 sur la droite des réels.
On la note |![]() | .
| .
-
- Exemple

Attention : On a donc :
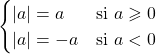
Distance entre deux nombres réels
- Propriété
Soient ![]() et
et ![]() deux nombres réels.
deux nombres réels.
La distance entre ![]() et
et ![]() est égale à |
est égale à |![]() | (ou |
| (ou |![]() | , ce qui est la même chose).
| , ce qui est la même chose).
-
- Exemple

−3 et 4 sont distants de 7 unités car ![]() =
= ![]() = 7.
= 7.
Retrouvez d’autres cours en ligne de maths seconde sur notre site :
- Fiche de cours sur l’arithmétique en seconde
- Cours sur les généralités sur les fonctions seconde générale
- Résumé de cours en fonctions et variations 2nde
- Cours complet sur les fonctions affines seconde
- Exercices et corrigés Ensembles et intervalles seconde
- Exercices et corrections arithmétique seconde générale